УДК: 621.391
Использование метода векторной аппроксимации для идентификации полюсной модели широкополосных микроволновых устройств
А. А. Валайтите, Е. В. Садовская, Т. Я. Шевгунов
Московский авиационный институт (национальный исследовательский университет)
Получена 25 августа 2013 г.
Аннотация. В настоящей работе представлено применение метода векторной аппроксимации для оценки параметров полюсной модели передаточной функции, описывающей микроволновые устройства в широком диапазоне частот. На примере данных, полученных при численном моделировании двухпортового микрополоскового фильтра, была идентифицирована комплексная полюсная модель восьмого порядка, описывающая частотную характеристику с высокой точностью в заданной широкой полосе.
Ключевые слова: широкополосные системы, микроволновые устройства, метод векторной аппроксимации, параметрическая идентификация.
Abstract. This paper presents the application of vector fitting method to the estimation of pole-model parameters proposed for transfer function of multiport wideband microwave devices. The example of system identification made for simulated data of microstrip two-port filter is demonstrated; the verification step shows the model consisting of eight poles approximates the frequency response of the device with very high accuracy.
Keywords: wideband systems, microwave devices, vector fitting method, system identification.
Введение
Задача проектирования микроволновых устройств привлекает активное внимание ученых и исследователей в течение нескольких последних десятилетий. Современные системы передачи информации, равно как и радиолокационные системы, имеют тенденцию к расширению полосы частот, занимаемой спектрами обрабатываемых в них сигналов, и, следовательно, актуальной становится задача проектирования широкополосных и сверхширокополосных микроволновых компонентов. Практически все современные подходы к проектированию микроволновых компонентов, обладающих требуемыми частотно-избирательными свойствами в широкой полосе частот, базируются на применении методов численного решения электродинамической задачи. Несмотря на два главных преимущества численного моделирования, универсальности и высокой точности, у него имеются собственные недостатки: с одной стороны, программная реализация любого метода решения интегральных уравнений требует значительных вычислительных ресурсов, а с другой стороны, получаемые результаты часто нуждаются в качественной интерпретации, проясняющей общие закономерности происходящих физических явлений.
В том случае, если исследуемые микроволновые устройства являются линейными, одним из путей аналитического решения данной проблемы, ведущим к получению компактных моделей, является применение системных передаточных функций устройства, представляющих собой комплексные полюсные модели:
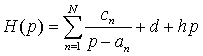 , (1)
, (1)
где an – полюса (действительные или комплексно-сопряженные), cn – вычеты, параметр d соответствует прямому прохождению сигнала, а коэффициент h описывает дифференцирующие свойства системы. Величина N определяет порядок полюсной модели.
При использовании полюсной модели возникает задача оценки её параметров по экспериментальным данным, как правило, представляющим собой частотные характеристики устройств, связывающие попарно сигналы в различных портах микроволнового устройства. Ключевой проблемой в оценке параметров модели по частотной характеристики, является существенно нелинейный характер зависимости модели от параметров полюсов {an}, входящих в знаменатели простых дробей в разложении (1).
Метод векторной аппроксимации
Одним из возможных подходов для решения которой может быть использован метод векторной аппроксимации, впервые подробно описанный в работе [1]. Метод векторной аппроксимации (Vector Fitting) является надежным инструментом системного моделирования, позволяющий обходить две проблемы рационального приближения: нелинейное оценивание и плохую обусловленность [1,6,8].
Благодаря сравнительно простой реализации в современных системах компьютерной математики, высокой точности и надежности метод был высоко оценен зарубежными учеными и использован ими в исследованиях устройств и систем передачи электрической энергии в работах [4] и [5]. Изначально метод был применен именно для моделирования передаточных функций линий электропередач [6], но впоследствии также нашел свое применение при построении компактных моделей частотных характеристик цепей сосредоточенных параметров, анализа промышленных сетей распределения электрической энергии. Проектирование и непосредственное использование данных моделирования представлено в работе [7]. В отечественной научной литературе рассматриваемый метод пока не нашёл широкого применения, но для знакомства с его теорией могут быть использованы работы [11,12]. Примеры успешного приложения метода для идентификации систем по исследуемой частотной характеристике могут быть найдены в работе [2], а параметрической идентификации сверхширокополосных микроволновых устройств в [3].
За последние годы данный метод претерпел изменения, направленные на достижение более высокой точности, ускорения сходимости и уменьшения влияния начального набора полюсов. Учеными были описаны способы установления наилучшей позиции полюсов [8], результаты расчетов для которого показывают значительное улучшение указанных выше показателей при использовании данных, искаженных шумом. На данный момент недостатком метода векторной аппроксимации остаётся его неэффективность при синтезе моделей, состоящих из большого числа полюсов, при исследовании устройства с относительно большим количеством портов; эта проблема была рассмотрена в работе [9].
Экспериментальное исследование
В экспериментальной части настоящего исследования решалась задача оценки параметров полюсной модели для передаточных характеристик микроволновых устройств, смоделированного численными методами. Исследование выполнено на примере оценки полюсов частотных характеристик, описывающих матрицу рассеяния микрополоскового фильтра, расчёт которого был выполнен использованием программы численного электродинамического моделирования HFSS Ansoft. Для этого была выбрана известная учебно-практическая модель микрополоскового фильтра, подробно рассмотренная авторами пособий [10].
Параметры, формирующие S-матрицу (матрицу рассеяния) устройства были получены с требуемым шагом, используя средства программы моделирования за счёт выбора соответствующих установок, включающих в себя:
· Общую характеристику решаемой задачи, в т.ч. желаемую точность решения.
· Параметры адаптивного измельчения сетки, если необходимо изменить характер измельчения сетки при плохой сходимости решения.
· Параметры частотной развертки (диапазон и шаг), для получения решения в диапазоне частот.
После получения в программе моделирования исследуемых частотных характеристик, представляющих собой S-параметры в виде наборов данных в широком диапазоне частот, производился расчет набора полюсов на соответствующем интервале частот с использованием итерационной процедуры векторной аппроксимации при известной частотной характеристике
На рис. 1 представлены амплитудно-частотные характеристики, представляющие собой зависимости от частоты модулей коэффициентов S11 и S12 для микрополоскового фильтра. Данные характеристики были получены в сверхширокой полосе частот, занимающей диапазон от 5 до 15 ГГц.

Рис. 1.Частотные характеристики фильтра.
На рис. 2 в качестве иллюстрации представлено распределение интенсивности электрического поля при гармоническом режиме с частотой 10 ГГц.
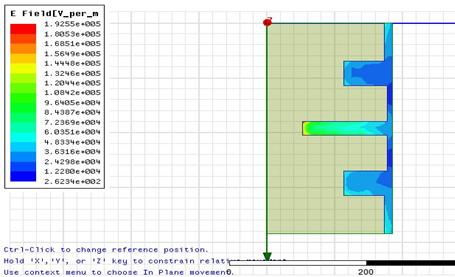
Рис. 2.Распределение интенсивности электрического поля.
Для обработки частотных характеристик авторами была разработана специализированная подпрограмма в пакете Matlab, оценивающая параметры линейной модели микроволнового устройства по известным отчетам комплексной частотной характеристики. Для ее практической реализации авторами работы была использована библиотека функций, представленная разработчиками оригинального метода векторной аппроксимации [1,6,8].
Для 501 частотной точки и 8 полюсов расчёт двадцати итераций в программе Matlab, запущенном на компьютере с процессором Pentium-IV с тактовой частотой 2,0 ГГц под управлением Windows 7 занял 10,7 секунд.
На рис. 3 представлено сравнение АЧХ для S21. Синей линией (Data) представлен график, построенный по экспериментальным данным, а красной (FRVF) – график, построенный по аналитической модели, состоящий из 8 полюсов. Как следует из графика, кривые полностью совпадают, а их разность (Deviation) пренебрежимо мала и существенно зависит от выбираемого порядка полюсной модели. Интегральное значение этой ошибки, оцениваемое среднеквадратическим отклонением, равно 5,8∙10−5, что соответствует очень высокой точности аппроксимации.
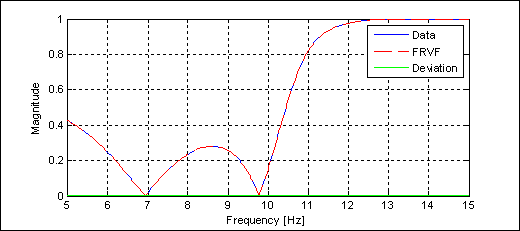
Рис. 3. Результат векторной аппроксимации
Интегральная зависимость точности аппроксимации от выбираемого порядка полюсной модели оценивается с помощью среднеквадратической ошибки, вычисляемой по формуле:
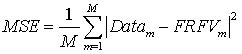 , (2)
, (2)
где M – число отсчётов частотных характеристик, Data и FRFV – соответственно данные моделирования и частотная, восстановленная по параметрам, оцененным методом векторной аппроксимации.
Зависимость среднеквадратической ошибки от порядка модели представлена на рис. 4. Как следует из графика, при порядке N = 8, точность существенно возрастает по сравнению с меньшими порядками, а вот дальнейшее увеличение порядка уже не приводит к существенному уменьшению среднеквадратической ошибки.
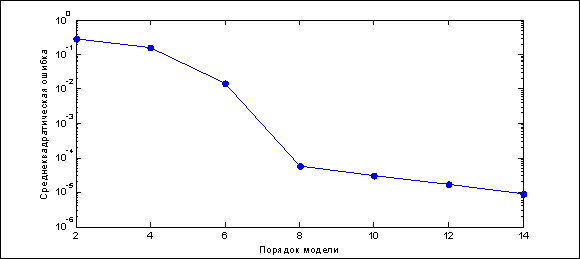
Рис. 4. Точность аппроксимации в зависимости от порядка модели.

Рис. 5. Диаграмма полюсов.
Отдельный интерес представляет диаграмма полюсов, которая изображена на рис. 5. При визуальном анализе этого рисунка можно ясно выделить две группы полюсов: пять полюсов, расположенных на эллипсе справа, и три оставшихся полюса, которые лежат далеко за его пределами – им соответствуют компоненты собственных частот с высоким затуханием.
Заключение
В настоящей работе описан результат применения метода векторной аппроксимации для оценки параметров полюсной модели передаточной функции, описывающей микроволновое устройство в широком диапазоне частот. Для идентификации параметров предложен последовательный алгоритм, включающий в себя: численное моделирование устройства, формирование частотных характеристик устройства, оценку параметров линейной модели, верификацию передаточной функции. Его практическая реализация была осуществлена в пакете Matlab. Результат моделирования показал, что для выбранного микрополоскового фильтра полюсная модель восьмого порядка, параметры которой оцениваются с помощью метода векторной аппроксимации, позволяет описать частотную характеристику фильтра в полосе от 5 до 15 ГГц с помощью восьми полюсов. Среднеквадратическая погрешность приближения при этом составляет менее десятой доли процента. Дальнейшее увеличение порядка модели не является целесообразным, в связи с появлением нестабильных полюсов. Представленная работа является исследованием в рамках общей задачи поиска и разработки эффективных методов проектирования широкополосных микроволновых устройств, решение которой ведется в рамках российских и международных исследовательских проектов.
1. B. Gustavsen and A. Semlyen, “Rational approximation of frequency domain responses by vector fitting”, IEEE Trans. on Power Del., vol. 14, no. 3, Jul. 1999, pp. 1052–1061.
2. Шевгунов Т.Я., Баев А.Б., Кузнецов Ю.В., Применение метода векторной аппроксимации для идентификации системы по частотной характеристике // Труды 9-ой Международной конференции «Цифровая обработка сигналов и ее применение», стр. 251–254, М.: ИПУ РАН, 2007.
3. Шевгунов Т.Я, «Параметрическая идентификация сверхширокополосных микроволновых устройств» – LAP Lambert Academic Publishing, Saarbrucken, Germany, 2011 – ISBN: 978-3-8443-5534-5.
4. Chi-Un Lei, Yuanzhe Wang, Quan Chen and Ngai Wong, “On Vector Fitting Methods in Signal/Power Integrity Applications”, IMECS-2010, vol. II.
5. S. Grivet-Talocia, “Package Macromodeling via Time-Domain Vector Fitting”, IEEE Microwave and wireless components letters, vol. 13, no. 11, Nov 2003, pp. 472–475.
6. B. Gustavsen and A. Semlyen, “Simulation of transmission line transients using vector fitting and modal decomposition”, IEEE Trans. in Power Delivery, vol. 13, no. 2, pp. 605–614, Apr. 1998.
7. M. Swaminathan et al., “Designing and Modeling for Power Integrity”, IEEE Trans. on electromagn. comp., vol. 52, no. 2, May 2010, pp. 288–310.
8. B. Gustavsen, “Improving the Pole Relocating Properties of Vector Fitting”, IEEE Trans. on Power Delivery, Vol. 21, no. 3, Jul. 2006, pp. 1587–1592.
9. S. Grivet Talocia and A. Ubollu, “On the generation of large passive macromodels for complex interconnect structures”, IEEE Trans. on Adv. Packag., vol. 29, no. 1, Feb. 2006, pp. 39–54.
10. Банков С.Е., Курушин А.А, “Расчет антенн и СВЧ структур с помощью HFSS Ansoft” – М.: ЗАО «НПП «РОДНИК», 2009, 256 с.
11. Т.Я. Шевгунов, Баев А.Б., Кузнецов Ю.В., Идентификация системы по известной частотной характеристике с использованием метода векторной аппроксимации // научный журнал «Информационно-измерительные и управляющие системы», М.: «Радиотехника», №11, 2007, стр. 55–59.
12. Т.Я. Шевгунов, Применение метода векторной аппроксимации в задачах параметрической идентификации линейных радиотехнических устройств // «Радиотехнические и телекоммуникационные системы», Муром, №4, 2011, стр. 45–49.