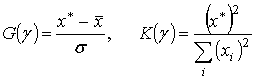УДК 621.371.5; 550.388.2

Адаптация стандартных критериев тестирования статистических выбросов для выделения сигнала ЛЧМ-ионозонда

 

А. Е. Недопекин

Марийский государственный университет

 

Получена 26 августа 2013 г.

 

Аннотация. В работе приведена разработка критериев выделения сигнала ЛЧМ-ионозонда в частотной области. Критерии основаны на стандартных статистиках Граббса и Кохрена, используемых в математической статистике для выбраковки аномальных отсчетов. Для данных статистик проведено исследование и найдены закономерности, выраженные через статистические параметры анализируемых выборок. Проведена апробация полученных критериев в полуэмпирическом моделировании и натурном эксперименте.

Ключевые слова: ионосфера, априорная неопределенность, выделение сигнала, моделирование

Abstract: Criteria developed for the separation of the signal chirp ionosonde in the frequency domain. The criteria are based on standard statistics Grubbs and Cochran, which are used in mathematical statistics for rejection of anomalous readings. For these statistics and the study found patterns, expressed in terms of statistical parameters of the analyzed samples. The approbation received by the criteria in the semiempirical modeling and full-scale experiment.

Key words: ionosphere, a priory indeterminacy, extraction of signal, modeling

 

Введение На сегодняшний день широкое применение в ионосферных исследованиях имеют ионозонды, использующие линейно-частотную модуляцию (ЛЧМ) зондирующего коротковолнового (КВ) сигнала [1]. Однако, несмотря на ряд очевидных достоинств, как-то: хорошую помехозащищенность, малое энергопотребление передатчика, широкий частотный диапазон измерений, — ЛЧМ-зондирование сопряжено с некоторыми сложностями, связанными с характером среды распространения сигнала. В широкую полосу полезного ЛЧМ-сигнала попадают сигналы множества посторонних радиотехнических устройств (РПУ) неизвестной частотно-временной структуры, так же сказывается и нестационарный характер среды распространения сигнала [2]. Все это вместе делает статистический анализ принятого сигнала затрудненным даже при использовании когерентного приема зондирующего сигнала [3]. Становится актуальным обоснование и разработка подходов выделения в частотной области полезного сигнала ЛЧМ-зондирования.

В работе [4] выделение рассматриваемого сигнала предлагается проводить после построения всей развертки спектров по частоте зондирования (ионограммы) путем использования пороговой фильтрации по уровню квантилей, при этом рассматриваются все данные, то есть порог выставляется сразу для всех спектров сигнала из сеанса зондирования. Данный способ, использующий по терминологии [5] «глобальную обработку», может давать малую ошибку пропуска сигнала, но требует затем тщательной фильтрации для устранения ложно выделенных отсчетов.

В работе [6] использован более подходящий для нестационарного сигнала «локальный подход» на уровне отдельных спектров сигнала в частотной области. Но при этом предполагается, что смесь сигнал-шум распределена по рэлеевскому закону, аналогично случаю узкополосного сигнала. Использованный же критерий выделения сигнала основан на поиске точки выпуклости графика функции распределения вероятностей для спектральной выборки. Эта точка выступает в качестве разграничителя между отсчетами сигнала и шума. Такой подход к выделению дает очень малую ошибку пропуска сигнала, но избавление от выделенных также сосредоточенных помех и большого количества ложных отсчетов превращается в труднореализуемую задачу.

В работе [7] приводятся результаты, которые утверждают, что обработка ЛЧМ-сигнала в частотной области проходит в условиях априорной непараметрической неопределенности. Преобладающие законы распределения для шума и смеси сигнал-шум отсутствуют, а сами законы распределения претерпевают постоянные изменения.

Целью работы является разработка статистических критериев выделения сигнала ЛЧМ-ионозонда в частотной области в условиях априорной непараметрической неопределенности.

2. Подход к выделению сигнала

После перемножения в приемнике принятого сигнала ионосферного распространения на сигнал гетеродина, когерентный излучаемому сигналу, происходит выделение сигнала разностной частоты, который представляет собой смесь квазигармонического полезного сигнала, шума ДКМ-диапазона и некоторого количества неизвестных помех. Обработка сигнала проходит поблочно в частотной области: весь оцифрованный сигнал разбивается на элементы анализа длительностью  и для каждого элемента производится переход в частотную область через быстрое преобразование Фурье [8].

В работах [2, 9] для структурного описания анализируемых спектральных выборок описывается качественная модель, которая представляет выборку в частотной области как сумму двух компонент из разных генеральных совокупностей с существенно различающимися параметрами: При этом весовой коэффициент компоненты, соответствующей сигналу, много меньше аналогичного коэффициента для компоненты шума. Для качественной модели не делается никаких выводов или предположений о виде распределений указанных компонент, то есть модель является непараметрической. В качестве вывода утверждается, что выделение в спектре отсчетов полезного сигнала, малочисленных по сравнению с прочими отсчетами, может быть сведено к задаче цензурирования или тестирования выборки на аномальные отсчеты, в роли которых выступают отсчеты сигнала. Пример ионограммы и спектров сигнала для сеанса зондирования Норильск—Йошкар-Ола (22.02.2010 г., 11 ч. 58 мин. МСК ) представлены на рис. 1 a) и b) соответственно. Область, выделенная рамкой на рис. 1 а) соответствует спектрам, изображенным на рис. 1 б). На рисунке  — центральная частота элемента зондирования,  — разностная частота в спектре обрабатываемого блока данных,  — время группового запаздывания сигнала.

 

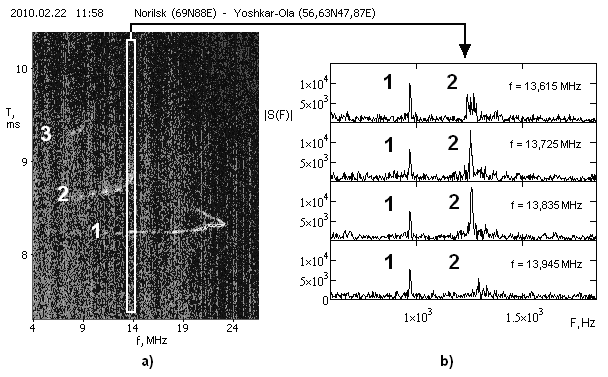
Рис. 1 Пример ионограммы и спектров сигнала

Представленный на рисунке сигнал является многомодовым, моды пронумерованы арабскими цифрами, две из них попали в выделенную область рис. 1 а) — их поведение отражено на рис. 1 б).

Новая постановка задачи требует использования критериев цензурирования. Хорошо известны критерии цензурирования, табулированные для случая тестирования выборки из генеральной совокупности, подчиняющейся нормальному закону [10]. Однако в работах [11-12] приводится адаптация для статистики Граббса для некоторых распределений, отличных от нормального. В качестве используемых статистик рассмотрим статистики Граббса  и Кохрена  в зависимости от некоторых параметров  анализируемых выборок:

 

,                         (1)

где  — тестируемый отсчет,  — часть анализируемой выборки из  отсчетов, выступающая в качестве эталона без аномалий,  и  — среднее выборочное и среднеквадратическое отклонение этой части выборки. Для данных формул превышение правой частью выражений критического значения  или , вычисленного для данных эмпирических значений , будет означать принадлежность отсчета  к статистическим выбросам или, в данном случае, к полезному сигналу.

 

3. Установление зависимостей

Для анализируемых данных было проведено обучение критериев (1) с целью установления зависимостей критических значений статистик  и  от параметров выборок. В качестве параметров , помимо , были выбраны такие формообразующие для распределения параметры как эксцесс  и асимметрия . В качестве обучающих наборов данных выступали выборки сигнала в частотной области различного объема, полученные при различных параметрах зондирования. Всего было рассмотрено 95000 выборок из наборов сеансов в различное время суток и года в различных геофизических условиях, отобранных за период 2009-2010 г.г. Пункт приема сигнала — г. Йошкар-Ола, пункты передачи: Норильск, ст. Горьковская, Sodankila (Финляндия). Выборки нормировались своим максимальным значением, что обеспечило нормированность их статистических характеристик. Затем проводилось полуэмпирическое моделирование смесей сигнал-шум с участием эмпирических сигналов и шумов. Установлено, что рассмотренные «формообразующие» распределение параметры, такие как асимметрия и эксцесс имеют высокое значение корреляции: в среднем 0,91, что делает нецелесообразным использование двух параметров одновременно. В качестве параметра  был выбран эксцесс, поскольку при наличии сигнала он имеет наибольшую линейную и ранговую корреляции с отношением сигнал/шум равные соответственно -0,89 и -0,943. На рис. 2 а) и b) представлены графики  и  соответственно, огибающие множество точек для рассмотренных выборок.

 

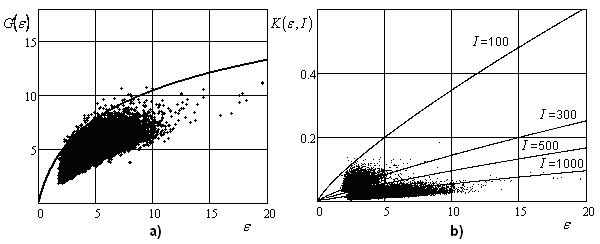
Рис.2. Результаты вычислительного эксперимента и огибающие кривые

Для статистики Кохрена, в отличие от статистики Граббса, выразилась зависимость от размера выборки. Огибающие кривые, соответствующие ошибке ложного обнаружения 0,1%, имеют следующий установленный вид:

 

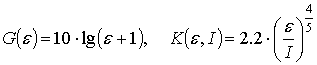.                      (2)

Учитывая тот факт, что среднее количество отсчетов, соответствующих наличию различимого сигнала в частотной области, равно 1-5%, в качестве значения  целесообразно выбирать первые 90-95% вариационного ряда выборки, по которым и будет производиться расчет параметров, а тестированию подвергать последние 5-10% вариационного ряда.

 

4. Апробация

Было проведено полуэмпирическое моделирование с использованием экспериментальных данных, содержащих сигнал и содержащих только шум. Мощность шума подвергалась варьированию с целью получения выборок, в которых бы отношение сигнал/шум было меньше единицы. Было обработано около 11000 спектральных выборок на предмет изучения ошибок пропуска сигнала, ошибок ложного обнаружения, а также ложного обнаружения в выборках, не содержащих сигнал — числа «ложных» спектров. Результаты для означенных критериев приведены в Таблице 1.

 

Таблица 1.

Параметр   Критерий	Порог 5% ошибки пропуска сигнала (дБ)	Ошибка ложного выделения (%)	«Ложные» спектры (%)
Статистика Граббса	7,8	0,167	3,962
Статистика Кохрена	9,1	0,015	0,806
Критерий с квантилем 95%	7,7	0,13	3,4

 

В первом столбце таблицы представлен порог отношения сигнал/шум, при котором достигается ошибка пропуска сигнала не более 5%. Ошибка ложного обнаружения считается по всем шумовым отсчетам ионограммы, «ложные» спектры — число спектров элементов анализа сигнала в сеансе, в которых отсутствовал сигнал, но для которых, тем не менее, было проведено ошибочное выделение. Для сравнения с указанными критериями использован критерий, полученный из первичного анализа результатов [7] и использующий нормированный максимальным значением выборки квантиль порядка 95% [13]. Как видно, этот критерий проигрывает новому критерию со статистикой Кохрена по ошибке ложного выделения примерно в 8,5 раз.

В качестве экспериментальной апробации было использовано определение максимальной наблюдаемой частоты (МНЧ) распространения зондирующего сигнала . На ионограмме (рис. 1) этой частоте будет соответствовать последний спектр в сеансе (столбец ионограммы), содержащий полезный сигнал. Нахождение этого спектра осуществлялось после выделения сигнала. Было рассмотрено несколько трасс зондирования. На рис. 3 а) приведен пример хода МНЧ, измеренной оператором (толстая линия) для трассы Инскип (Великобритания)‑Йошкар-Ола в указанный на рисунке период, и МНЧ, измеренной автоматически после выделения сигнала и медианной фильтрации очищенных от шума данных ионограммы. То же самое для трассы Франция‑Йошкар-Ола — на рис. 3 б). Средняя относительная ошибка составила для критерия со статистикой Граббса 2,70%, для критерия со статистикой Кохрена — 2,64%. Среднеквадратические отклонения для критериев составили соответственно 7,39% и 6,64%. Всего было рассмотрено около 700 сеансов зондирования для 2009 и 2011 г.г. на четырех трассах с исходными пунктами в г. Инскипе, г. Лионе (предположительно), ст. Горьковская (Ленинградская обл.), г. Диксоне и приемном пункте в г. Йошкар-Ола.

 

Рис. 3 Пример суточного хода МНЧ

 

5. Выводы

В работе на основе подхода, рассматривающего выделение сигнала в шумах как поиск аномальных отсчетов, путем применения статистик Кохрена и Граббса получены критерии выделения сигнала ЛЧМ-ионозонда, использующие статистическую зависимость между указанными статистиками и эксцессом анализируемых выборок. Критерии корректны с точки зрения условий неопределенности, в которых проходит обработка данных, используют статистические параметры текущих выборок без априорных или модельных предположений, но обеспечивают при этом относительное равновесие между ошибками пропуска сигнала и ложным обнаружением.

 

Литература

1.    Ivanov V.A.; Kurkin V.I.; Nosov V.E.; Uryadov V.P.; Shumaev V.V. “Chirp Ionosonde and Its Application in the Ionospheric Research” // Radiophysics and Quantum Electronic. 2003. Volume 46, Number 11, pp. 821-851.

2.    Колчев А.А., Щирый А.О. Режекция сосредоточенных по спектру помех при ЛЧМ-зондировании ионосферы // Известия вузов. Радиофизика. 2006. Т. 49, № 9. С. 751‑759.

3.    Колчев А.А., Шпак Д.Г. Квазиоптимальная обработка широкополосного сигнала с ЛЧМ // Научно-технические ведомости Санкт-Петербургского государственного политехнического университета. 2010, № 103. С. 48-52.

4.    Nicholas J. Redding The Autoscalling of Oblique ionograms, Research Report. Salisbury: Electronics and Surveillance Research Laboratory, 1999. 142 p.

5.    Галкин И.А. Программное обеспечение системы автоматической обработки ионограмм вертикального зондирования. I. Первичная обработка ионограммы: Препринт № 20-87. Иркутск: СибИЗМИР, 1987. 17 с.

6.    Рябова Н.В. Диагностика и имитационное моделирование помехоустойчивых декаметровых радиоканалов. Йошкар-Ола: МарГТУ, 2003.

7.    Колчев А.А., Недопекин А.Е. Экспериментальное подтверждение априорной непараметрической неопределённости для сигнала ЛЧМ-ионозонда в спектральной области // Вестник Национального технического университета «Харьковский политехнический институт». Сборник научных статей. Тематический выпуск: Радиофизика и ионосфера. Харьков: НТУ «ХПИ», 2011. № 44. С. 91-100.

8.    Филипп Н.Д., Блаунштейн Н.Ш., Ерухимов Л.М., Иванов В.А., Урядов В.П. Современные методы исследования динамических процессов в ионосфере. Кишинев: Штиинца, 1991. 286 с.

9.    Колчев А.А., Недопекин А.Е. Об одной модели смеси распределений вероятностей в радиотехнических измерениях // Компьютерные исследования и моделирование. 2012. Т.4. №3 С. 563-569.

10.  ГОСТ Р ИСО 5725-2-2002. Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. М.: Изд-во стандартов. 2002. 51 с.

11.  Лемешко Б.Ю. Робастные методы оценивания и отбраковка аномальных измерений // Заводская лаборатория. 1997. Т. 63. №5. С. 43-49

12.  Лемешко Б.Ю., Чимитова Е.В. Построение оптимальных L-оценок параметров сдвига и масштаба распределений по выборочным квантилям // Сибирский журнал индустриальной математики. 2001. Т. 4. №2. С. 166-183.

13.  Колчев А.А., Недопекин А.Е. Методика выделения сигнала ЛЧМ-зондирования ионосферы на фоне шумов ДКМ-диапазона // XVIII Международная научно-техническая конференция «Радиолокация, навигация, связь» (RLNC’2012). Воронеж: НПФ «САКВОЕЕ» ООО, 2012. Т.1. C. 606-611.