УДК 621.3.09

ВЛИЯНИЕ ФИЗИКО-ХИМИЧЕСКИХ ХАРАКТЕРИСТИК МОРСКОЙ ВОДЫ НА РЕЗОНАНСНОЕ РАССЕЯНИЕ РАДИОВОЛН МОРСКОЙ ПОВЕРХНОСТЬЮ

 

А. С. Запевалов, В. В. Пустовойтенко

Морской гидрофизический институт

 

Статья получена 3 сентября 2014 г.

 

Аннотация. Анализируется взаимодействие радиоволн с морской поверхностью. Рассматриваются изменения радиосигнала, резонансно рассеянного назад морской поверхностью, в результате изменения диэлектрической проницаемости под границей раздела океан-атмосфера. Получены количественные оценки изменения геометрического коэффициента, вызванные вариациями температуры и солености морской воды. Анализ проведен для длин радиоволн миллиметрового, сантиметрового и дециметрового диапазонов.

Ключевые слова: относительная диэлектрическая проницаемость, морская поверхность, резонансное рассеяние радиоволн, температура, соленость.

Abstract: The interaction of radio waves with the sea surface is analyzed. Change of  radio signal, resonant back-scattered by sea surface, as a result of changes in the dielectric constant under the boundary of the ocean-atmosphere, are considered. The quantitative assessment of the  changes in the geometric factor caused by variations in temperature and salinity of sea water are calculated. The analysis is performed for the length of radio waves millimeter, centimeter and decimeter ranges.

Key words: complex dielectric constant, sea surface, Bragg scattering of radio waves, temperature, salinity.

 

Введение

С возникновением нового направления в океанографии, названного  радиоокеанографией, появилась возможность дистанционного мониторинга больших акваторий Мирового океана [1, 2]. Радиолокационные измерения океанографических и метеорологических параметров (таких как скорость приводного ветра, значимая высота волн и ряд других) относятся к группе косвенных измерений [3, 4]. Эффективность их применение во многом зависит от того, насколько полно и корректно учитываются все процессы, влияющие на взаимодействие радиоволн с морской поверхностью.

При анализе и интерпретации взаимодействия радиоволн с морской поверхностью необходимо учитывать изменения диэлектрической проницаемости морской воды [5, 6]. Эти изменения оказывают влияние на два основных физических механизма, определяющих формирование радиосигнала при однопозиционном зондировании морской поверхности – квазизеркальное отражение и резонансное (брегговское) рассеяние.

При зондировании морской поверхности в СВЧ-диапазоне в области углов падения, где доминирующим является резонансный механизм рассеяния, регистрируемый радиолокатором сигнал пропорционален геометрическому коэффициенту, который зависит от угла падения радиоволн и от относительной диэлектрической проницаемости среды под границей океан-атмосфера [5, 7]. Теоретические и экспериментальные исследования указывают на существование зависимости относительной диэлектрической проницаемости морской воды от ее температуры и солености [8, 9]. Этот эффект оказывает влияние на результаты мониторинга пограничных слоев атмосферы и океана средствами дистанционного зондирования, работающих в СВЧ-диапазоне.   радиоволн [10].

Целью настоящей работы является количественный анализ влияния физико-химических характеристик морской среды на изменения уровня радиосигнала, рассеянного назад поверхностными волнами.

 

1. Резонансное рассеяние радиоволн

В случае зондирования морской поверхности в области отсчитываемых от вертикали углов падения  от 25° до 75° - 80° рассеянный назад сигнал определяет резонансный (брегговский) механизм рассеяния [7]. Рассеяние радиоволн назад создают поверхностные волны, бегущие вдоль направления зондирования в прямом или обратном направлении, волновое число которых  связано с волновым числом радиоволн  резонансным соотношением .

В нулевом приближении, когда резонансные (брегговские) составляющие поля поверхностных волн распространяются по плоской поверхности, нормированное сечение обратного рассеяния можно представить в форме

 

,                             (1)

 

где  – вид поляризации, первый индекс соответствует поляризации излучаемого сигнала, второй – принимаемого; – геометрический коэффициент, зависящий от вида поляризации излучаемого и принимаемого радиолокационного сигнала и диэлектрической проницаемости морской воды;  – двумерный спектр возвышений морской поверхности, соответствующий волновому вектору  брегговской компоненты.

В приближениях более высоких порядков необходимо учитывать эффекты, которые связаны с присутствием волн более длинных, чем брегговские компоненты поля поверхностных волн [11]. Длинные волны изменяют локальные наклоны морской поверхности, и брегговские компоненты распространяются по наклонной поверхности. Соответственно изменяется условие резонанса и величина геометрического коэффициента. Чтобы учесть влияние длинных волн на величину рассеянного назад сигнала, необходимо выражение (1) усреднить по всему диапазону создаваемых ими углов наклонов морской поверхности . Усреднение осуществляется с весом, определяющим вероятность появления тех или иных значений угла ,

,

 

                     (2)

 

где – плотность вероятностей углов наклонов в направлении падения радиоволны [12].

Характеристикой, которая определяет зависимость рассеянного назад радиосигнала от физико-химических свойств морской воды, является геометрический коэффициент .  Данная зависимость возникает вследствие изменения относительной диэлектрической проницаемости морской воды при изменении ее температуры и солености. Для вертикальной () и горизонтальной () поляризации функция  соответственно имеет вид [5],

 

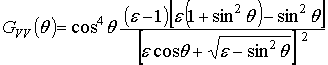,                           (3)

 

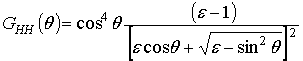.                               (4)

 

где  – относительная диэлектрическая проницаемость морской воды под поверхностью раздела атмосфера-океан.

 

2. Зависимость диэлектрической проницаемости воды от ее температуры и солености

Комплексная относительная диэлектрическая проницаемость морской воды является функцией трех параметров: температуры, солености и частоты. Активные экспериментальные исследования этой характеристики начались в середине прошлого века [8, 9, 13]. В последние десятилетия эти исследования вновь привлекают к себе пристальное внимание, что связано с развитием радиометрических средств контроля температуры и солености Мирового океана [14].

В настоящей работе воспользуемся моделью, описывающей связь относительной диэлектрической проницаемости морской воды с температурой, соленостью и частотой, которая предложена в работе [15]. Модель построена на основе двухчастотной аппроксимации Дебая в форме (обозначения авторов сохранены):

 

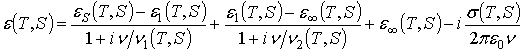,    (5)

 

 

где  – температура;  – соленость;  – статическая диэлектрическая проницаемость;  – промежуточный диэлектрический параметр;  – «оптическая» диэлектрическая проницаемость;  – частота;  и  – первая и вторая частоты релаксации Дебая;  – электропроводность воды [Сим/м],  – диэлектрическая постоянная ( ГГц м/Сим);   . Входящие в выражение (5) параметры имеют следующую размерность:  – [°С],  – [‰], ,  и  – [ГГц].

Зависимости от частоты  относительной диэлектрической проницаемости  при трех значениях солености и двух значениях температуры показаны на рис. 1. Видно, что мнимая часть  более чувствительна к изменениям температуры и солености, чем ее реальная часть. На низких частотах эта зависимость выражена сильнее, чем на высоких. Также, из рис. 1 следует, что характер зависимости  сильно зависит от частоты при всех значениях параметров  и .

 

 

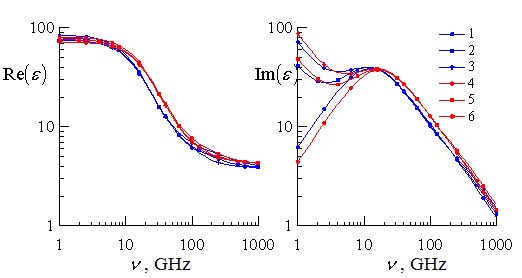
Рис. 1. Зависимости от частоты  реальной  и мнимой  составляющих относительной диэлектрической проницаемости.

Синие кривые соответствуют температуре 10 °С, красные – 20 °С;

кривые 1-3 и 4-6 соответствуют солености 0 ‰, 17 ‰, 34 ‰.

 

В настоящей работе мы анализируем резонансное рассеяние радиоволн на морской поверхности, где принято использовать не частоту , а длину волны . Поэтому при дальнейшем анализе будет использоваться параметр . Между собой частота и длина волны связаны соотношением , где  – скорость света.

На рис. 1 представлены зависимости от температуры действительной  и мнимой  частей относительной диэлектрической проницаемости морской воды на трех частотах 37.5, 10 и 3 ГГц, соответствующих длинам радиоволн 0.8, 3 и 10 см. Длины волн от 0.8 см до 10 см выбраны, чтобы перекрыть диапазон, в котором обычно работают радиолокационные средства зондирования океана, установленные на космических аппаратах.

Результаты анализа изменений относительной диэлектрической проницаемости в зависимости от изменений температуры и солености морской воды представлены на рис. 2 и рис. 3.

 

 

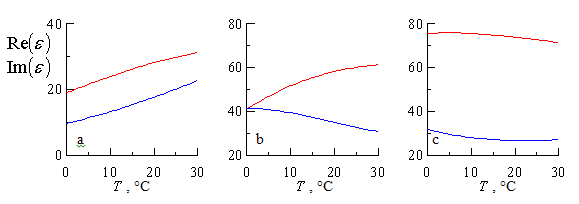
Рис. 2. Зависимости от температуры  действительной  (красная линия) и мнимой  (синяя линия) частей относительной диэлектрической проницаемости. Фрагменты a, b и с соответствуют длинам волн
0.8 см, 3 см и 10 см.

 

При построении рис. 2 было принято, что соленость равняется 17 ‰ . Такой уровень солености близок к солености черноморской воды. Из рис. 2 следует, что характер изменений  и  с ростом температуры существенно зависит от длины волны . С изменением длины волны, также, заметно меняются абсолютные значения действительной и мнимой частей относительной диэлектрической проницаемости.

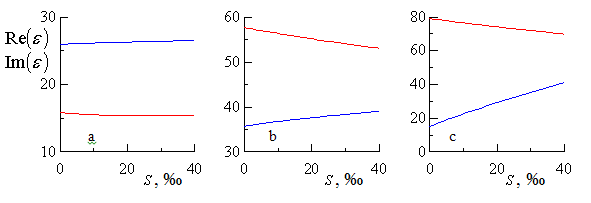
Рис. 3. Зависимости от солености  действительной  (красная линия) и мнимой  (синяя линия) частей относительной диэлектрической проницаемости. Фрагменты a, b и с соответствуют длинам волн

0.8 см, 3 см и 10 см.

Приведенные на рис. 3 зависимости от солености действительной  и мнимой  частей относительной диэлектрической проницаемости построены для температуры °C. Обращает на себя внимание, что при 0.8 см, абсолютная величина мнимой части  больше, чем действительной.

3. Зависимости геометрических коэффициентов от угла падения температуры и солености морской воды

Общий вид зависимости от угла падения, рассчитанный для трех длин волн на вертикальной и горизонтальной поляризации, показан на рис. 4. Из рис. 4a и 4b следует, что на вертикальной и горизонтальной поляризации геометрические коэффициенты, рассчитанные для длин волн ,  и  близки между собой. Также следует, что диапазон изменения  при изменении угла падения значительно шире, чем диапазон изменения .

 

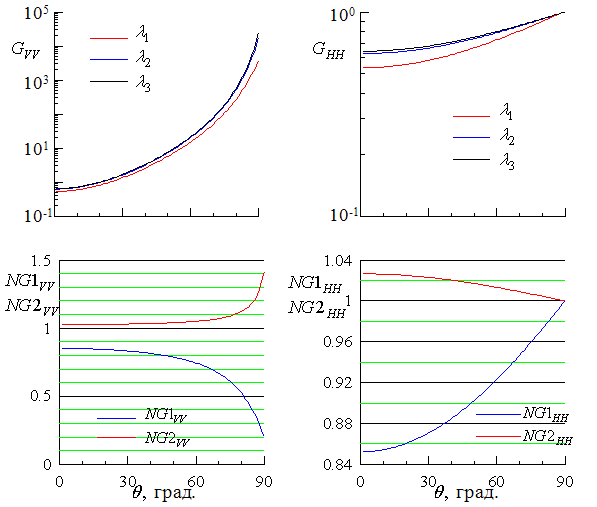
Рис. 4. Зависимости геометрических коэффициентов от угла падения
радиоволн на морскую поверхность

Следует отметить, что, хотя на рис. 4 построены изменения величин геометрических коэффициентов для углов  от 0° до 90°, практический интерес представляют изменения в более узком диапазоне. Это диапазон равняется

 

25°80°.                                                 (6)

 

При зондировании морской поверхности под углами 25° сигнал радиолокатора определяет физический механизм квазизеркального отражения. При зондировании под углами 80° необходимо учитывать целый ряд физических эффектов. В частности, необходимо учесть такой эффект, как затенение морской поверхности гребнями длинных доминантных волн [16].

Чтобы количественно оценить различия между геометрическими коэффициентами на выбранных длинах волн введем нормированные коэффициенты

 

,                                        (7)

 

.                                      (8)

 

В области 60° расхождения коэффициентов  менее 25 %, расхождение коэффициентов  во всем диапазоне изменения угла падения менее 10 %.

Проанализируем зависимость коэффициентов  при фиксированных значениях угла падения от солености и температуры. Будем рассматривать три угла падения 30°, 55° и 80°. Введем относительные изменения геометрических коэффициентов, описывающие их зависимость от солености и температуры

 

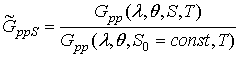,                                    (9)

 

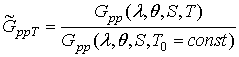.                                   (10)

 

 

Результаты расчетов параметров  и  приведены на рис. 5 и 6 соответственно.

Оценки  получены при значениях солености 17 ‰, для температуры 15 °С. Видно (см. рис. 5), что изменения солености в широких пределах слабо влияют на величину параметра . Изменения значений параметра  на обеих поляризациях не превышают 4 %, относительно значения, полученного при принятой в данной работе за опорную солености в 17 ‰, при условии, что соленость меняется в пределах от 0 ‰ (пресная вода) до 35 ‰ (океанская вода). 

 

 

 

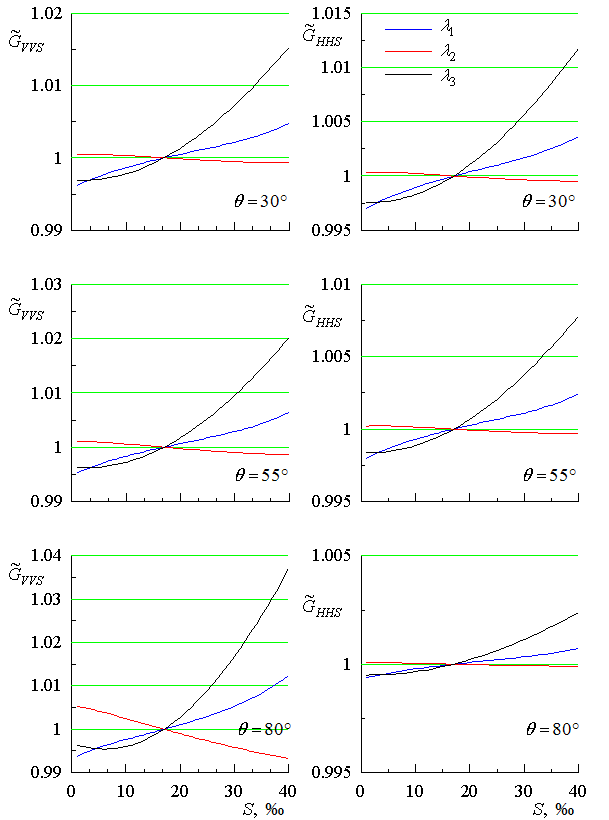
Рис. 5. Зависимости параметров  и  от солености 

 

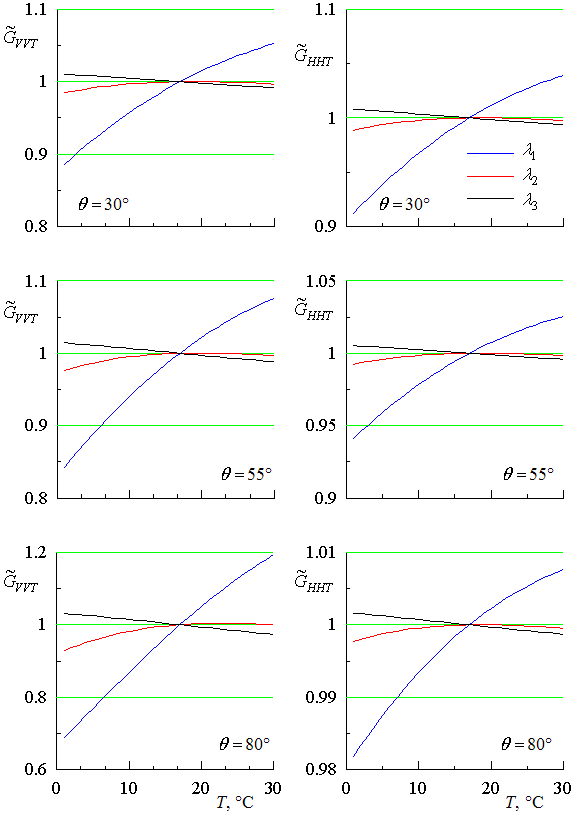
Рис. 6. Зависимости параметров  и  от температуры

 

Изменения значений параметра  происходит в более широких пределах (см. рис. 6). Здесь в качестве опорного принято значение температуры 15 °С. Сравнивая графики , построенные для разных углов падения, можно сделать вывод, что с ростом угла падения  зависимость параметра  от температуры возрастает. Изменения значений параметра  для угла падения 80° могут достигать 25 %.

В настоящее время основным источником информации о скорости ветра над различными акваториями Мирового океана являются данные спутниковых радиолокационных измерений. Полученные в настоящей работе результаты показывают, что при расчетах скорости ветра ошибками, обусловленными зависимостью сечения обратного рассеяния  от температуры и солености морской воды можно пренебречь. Таким образом, можно считать справедливой гипотезу о том, величина  однозначно определяется шероховатостью морской поверхности, формируемой короткими поверхностными волнами [3, 17].

 

Заключение

Анализ, результаты которого представлены в настоящей работе, показал следующее.

·        Геометрические коэффициенты на вертикальной поляризации , рассчитанные для длин волн  ,  и , также как геометрические коэффициенты на горизонтальной поляризации , близки между собой. Причем, диапазон изменения  при изменении угла падения в пределах от 0° до 90° на четыре порядка шире, чем диапазон изменения .

·        Изменения солености в пределах от солености пресной воды до солености океанской воды слабо влияет на величину геометрического коэффициента на обеих поляризациях. Изменения значений параметра  не превышают 4 %, относительно значения, полученного при солености 17 ‰.

·        Относительные (относительно значений полученных при 15 °С) изменения геометрических коэффициентов при изменениях температуры от 0 °С до 30 °С происходят в пределах 0.7 до 1.2. Причем с ростом угла падения зависимость геометрических коэффициентов от изменений температуры возрастает.

 

Литература

1. Басс Ф.Г., Брауде С.Я., Калмыков А.И., Мень А.В., Островский И.Е, Пустовойтенко В.В., Розенберг А.Д., Фукс И.М. Методы радиолокационных исследований морского волнения (радиоокеанография) // Успехи физических наук, 1975, т. 116, с. 741-743.  

2. Коротаев Г.К., Пустовойтенко В.В., Радайкина Л.Н. Информационные ре-сурсы космического экологического мониторинга морских акваторий // Экологическая безопасность прибрежной и шельфовой зон, 2004, т. 11, с. 198-212. 

3. Мур Р., Фэн А. К. Радиолокационное определение параметров ветра над морем // ТИИЭР, 1979, т. 67, с.40-63.

4. Запевалов А.С., Показеев К.В., Пустовойтенко В.В. О предельной точности альтиметрического определения скорости приводного ветра //Исследования Земли из космоса, 2006, № 3, с. 49-54.

5. Valenzuela G. Theories for the interaction of electromagnetic and ocean waves.- A Review // Boundary Layer Meteorology, 1978, vol. 13, № 1-4, -рр. 61-85.

6. Пустовойтенко В.В., Запевалов А.С. Оперативная океанография: Спутниковая альтиметрия – Современное состояние, перспективы и проблемы // Серия. Современные проблемы океанологии, Севастополь: НПЦ «ЭКОСИ-Гидрофизика», 2012, Вып. 11, 218 с.

7. Басс Ф.Г., Фукс И.М. Рассеяние волн на статистически неровной поверхности. М.: Наука, 1972, 424 с.

8. Рабинович Ю.И. Мелентьев В.В. Влияние температуры и солености на излучение гладкой водной поверхности в сантиметровом диапазоне // Труды ГГО, 1970, Вып. 235, с.78-123.

9. Hyatt H.A. Emission, reflection, and absorption of microwaves at a smooth air-water interface // J. Quanr. Specrrosc. Radim. Transfer, 1970, vol. 10, рр. 211-247.

10. Терехин Ю.В., Пустовойтенко В.В. Влияние температуры и солености морской воды на характеристики радиолокационного сигнала СВЧ-диапазона // Исследование Земли из космоса, 1986, № 2, с. 16-20.

11. Запевалов А.С. Моделирование брегговского рассеяния электромагнитного излучения сантиметрового диапазона морской поверхностью. Влияние волн более длинных, чем брегговские составляющие // Известия РАН. Физика атмосферы и океана, 2009, т. 45, № 2, с. 266-275.

12. Запевалов А.С., Пустовойтенко В.В. Моделирование плотности вероятностей уклонов морской поверхности в задачах рассеяния радиоволн // Известия ВУЗов. Радиофизика, 2010, т. 53, № 2, с. 110-121.

13. Klein, L.A., Swift C.T. An improved model for the dielectric constant of sea water at microwave frequencies // IEEE Truns. Ant. Prop., 1977, AP-25, рр. 104-111.

14. Садовский И.Н., Кузьмин А.В., Шарков Е.А., Сазонов Д.С., Пашинов Е.В., Ашеко А.А., Батулин С.А. Анализ моделей диэлектрической проницаемости водной среды, используемых в задачах дистанционного зондирования акваторий // Препринт. М.: ИКИ РАН, 2002, Пр-2172, 60 с.

15. Meissner T., Wentz F.J. The complex dielectric constant of pure and sea water from microwave satellite observations // IEEE Transactions on Geoscience and Remote Sensing, 2004, vol. 42, No. 9, рр. 1836-1849.

16. Ерёмка В.Д., Кабанов В.А., Логвинов Ю.Ф., Мыценко И.М., Разсказовс-кий В.Б., Роенко А.Н. / под ред. д.т.н., проф. Разсказовского В.Б. Особенности распространения радиоволн над морской поверхностью. Севастополь: Вебер, 2013. 217 с.

17. Христофоров Г.Н., Запевалов А.С., Смолов В.Е. О предельной точности скаттерометрического определения со спутника скорости ветра над океаном // Исследование Земли из космоса, 1987, № 2, с. 57-65.