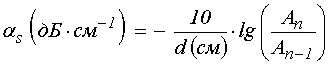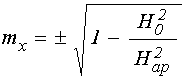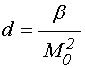Распространение магнитоупругих ультразвуковых импульсов в пластинах поликристаллического железоиттриевого граната в условиях неоднородного внутреннего поля. Часть 1. Поперечное намагничивание.

УДК 537.874; 537.624

РАСПРОСТРАНЕНИЕ МАГНИТОУПРУГИХ УЛЬТРАЗВУКОВЫХ ИМПУЛЬСОВ В ПЛАСТИНАХ ПОЛИКРИСТАЛЛИЧЕСКОГО ЖЕЛЕЗОИТТРИЕВОГО ГРАНАТА В УСЛОВИЯХ НЕОДНОРОДНОГО ВНУТРЕННЕГО ПОЛЯ

ЧАСТЬ 1. ПОПЕРЕЧНОЕ НАМАГНИЧИВАНИЕ

Д. С. Безносиков ¹, В. С. Власов ¹, В. Г. Шавров ², В. И. Щеглов ²

¹Сыктывкарский государственный университет, Сыктывкар, Россия

²Институт радиотехники и электроники РАН, Москва, Россия

Статья получена 16 сентября 2014 г.

Аннотация. Выполнено экспериментальное исследование распространения поперечных упругих волн в образцах из поликристаллического железоиттриевого граната при намагничивании полем, перпендикулярным направлению распространения волны. Для теоретической интерпретации наблюдаемых явлений предложена модель ориентационного перехода векторов намагниченности в доменах. Обнаружено явление затягивания ориентационного перехода, для интерпретации которого предложена модель, состоящая в несимметричном росте полей замыкающих доменов разных знаков. Выявлены два механизма затухания упругой волны в образце с доменами: раскачка намагниченности и возбуждение обменных спиновых волн. Показано, что теоретические положения описывают эксперимент с точностью не хуже 5%.

Ключевые слова: упругая волна, затухание, магнитоупругое взаимодействие, доменная структура.

Abstract. The experimental investigation of transverse elastic waves propagation in poly-crystal yttrium iron garnet specimens biased by magnetic field normal to propagation wave direction is made. For theoretical interpretation of observed phenomena it is proposed the model of domain magnetization vectors orientational transition. It is found the phenomenon of orientational transition delay. For its interpretation the model of asymmetrical increasing of different signs closed domain fields is proposed. It is found two mechanisms of elastic wave decay in specimen with domains: the swing magnetization vectors and exchange waves excitation. It is shown that theoretical model results describe the experiments in accuracy not less than 5%.

Key words: elastic wave, damping, magnetoelastic interaction, domain structure.

Введение

Ультразвуковые колебания высоких частот 10-100 МГц находят широкое применение в технике и научных исследованиях [1-3]. Важное место в телевизионной технике и аналоговой обработке информации занимает использование акустических поверхностных волн [4-7]. Традиционным способом возбуждения ультразвука на частотах до 50 МГц является использование резонансных преобразователей на пластинах из пьезоэлектрика [8], однако с повышением частоты пластины становятся настолько тонкими и хрупкими, что их использование становятся затруднительным. Важную роль на этих частотах играют магнитострикционные преобразователи [9-11], в том числе с использованием ферромагнитного резонанса (ФМР) вплоть до частот в десятки ГГц [12,13]. Эффективное возбуждение упругих колебаний на частотах до нескольких МГц возможно за счет использования движения доменных стенок в пленках ферритов-гранатов в условиях ориентационного перехода [14,15].

Перспективным магнитным материалом для высокочастотного ультразвука является железоиттриевый гранат (ЖИГ), акустическая добротность которого может на два порядка превосходить добротность кварца [1,13]. Для задержки упругого импульса на время порядка требуется монокристалл ЖИГ длиной . [13,16], изготовление которого требует немалого времени и обходится весьма дорого. Намного более простым и дешевым является поликристаллический ЖИГ, размеры образца из которого могут достигать десяти и более сантиметров. Введение алюминия, аналогичное применяемым для преобразователей на железе [1], позволяет в широких пределах менять намагниченность насыщения материала.

Работа устройства в условиях неоднородного поля, в том числе в присутствии доменной структуры, широко применяемая в технике магнитостатических волн [17-24], также значительно увеличивает его функциональные возможности [25-28]. Некоторые вопросы распространения магнитоупругих волн в условиях неоднородного намагничивания, в том числе в присутствии доменной структуры, частично рассмотрены в работах [29-31], однако проведенное там рассмотрение является существенно неполным. Так в работе [29], в части, посвященной «низкочастотному магнитоакустическому резонансу», то есть области частот ниже 100 МГц, неоднократно упоминается о необходимости учета доменной структуры, по мнению авторов, могущей оказать существенное влияние на свойства магнитоупругих волн, однако какой-либо попытки учесть домены не сделано. То же касается работы [30]. В работе [31] эксперименты по возбуждению ультразвука пленкой ЖИГ, выполненные на частотах 36 и 16 МГц, трактуются с позиции резонанса доменных границ (РДГ), однако приведенная там количественная оценка частоты РДГ в ЖИГ, основанная на работе [32], по-видимому, требует уточнения.

Таким образом, можно заключить, что имеющиеся на сегодняшний день исследования распространения магнитоупругих волн в образцах с неоднородным внутренним полем, в том числе с доменами, являются недостаточными.

В связи с этим, основной целью настоящей работы явилось исследование распространения коротких ультразвуковых импульсов в поликристаллических образцах легированного алюминием железоиттриевого граната в условиях неоднородного внутреннего поля, обеспечиваемого как за счет размагничивающих факторов формы протяженного образца, так и достаточно разветвленной доменной структуры.

1. Экспериментальная установка и методика измерений

Рассмотрим схему экспериментальной установки, основные параметры образцов и методику измерений.

1.1. Схема установки

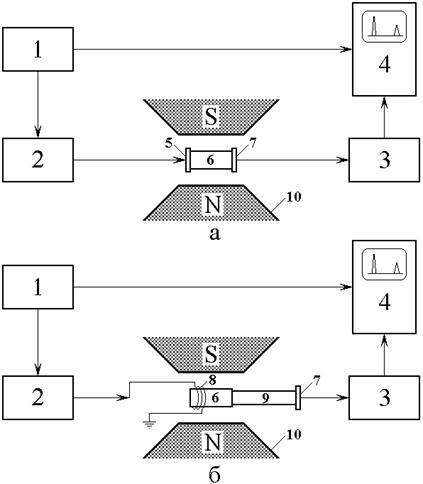
Измерения проводились классическим импульсным методом [2, 33-38] с помощью установки, упрощенная схема которой показана на рис.1.

Рис.1. Схема экспериментальной установки.

а – возбуждение механическое; б – возбуждение электромагнитное.

1 – генератор импульсов постоянного тока; 2 – генератор ВЧ сигнала; 3 – приемник ВЧ сигнала; 4 – осциллограф; 5 – излучающий пьезопреобразователь; 6 – образец; 7 – приемный пьезопреобразователь; 8 – возбуждающая катушка; 9 – звукопровод; 10 – магнит.

Основу установки составлял генератор импульсов постоянного тока 1, с которого задающие импульсы в качестве модулирующих поступали на генератор высокочастотного сигнала 2 и в качестве синхронизирующих на осциллограф 4. Высокочастотный импульсный сигнал поступал на образец 6, после взаимодействия с которым проходил на приемник 3, с выхода которого поступал на осциллограф 4. Магнитное поле в образце создавалось электромагнитом 10.

Установка работала «на проход» в двух различных режимах, отличающихся способом возбуждения упругих колебаний в образце.

На рис.1а показана схема работы установки при механическом возбуждении упругих колебаний. В этом случае на обоих торцах образца 6 размещались пьезопреобразователи – излучающий 5 и приемный 7, из которых первый был соединен с выходом генератора 2, а второй – со входом приемника 3.

На рис.1б показана схема работы установки при электромагнитном возбуждении упругих колебаний за счет магнитострикции образца. В этом случае вблизи одного торца образца размещалась возбуждающая катушка 8, а другой через звукопровод 9 был соединен с приемным пьезопреобразователем 7, сигнал с которого поступал на приемник 3.

Генератор импульсов 1 позволял формировать импульсы постоянного тока длительностью от 0.1 до 100 мкс с аналогичной паузой и амплитудой в единицы вольт. Генератор высокочастотного сигнала 2 обеспечивал радиоимпульсы той же длительности с частотой заполнения от 2 до 20 МГц и амплитудой до нескольких вольт. В некоторых экспериментах для повышения уровня возбуждения использовался дополнительный усилитель на лампе ГИ-30, позволявший получать в импульсе мощность до 100 Вт. В качестве приемника 3 использовался тракт прямого усиления, содержащий несколько резонансных каскадов, выполненных на транзисторах в каскодном включении. Чувствительность тракта составляла 10 мкВ, полоса пропускания регулировалась от 0.3 до 2.5 МГц. Электромагнит 10 питался током до 10 А от источника напряжением до 15 В, что при диаметре полюсов 120 мм позволяло в зазоре до 40 мм получать поле до 4500 Э. В некоторых экспериментах, в первую очередь при намагничивании образца вдоль его длинного размера, в качестве магнита 10 использовался соленоид с внутренним диаметром 30 мм и длиной 400 мм, питаемый от того же источника, что позволяло получить поле до 400 Э.

В качестве пьезопреобразователей использовались кварцевые пластины XY-среза с резонансной частотой 18.9 МГц на поперечной сдвиговой волне. Возбуждение преобразователей осуществлялось в резонансном режиме, то есть частота возбуждающего сигнала равнялась 18.9 МГц. Связующей склейкой между преобразователями, образцом и звукопроводом для поперечных волн являлась канифольно-восковая смесь. Звукопровод из плавленого кварца имел поперечное сечение порядка 5 на 5 мм и длину от 50 до 70 мм. Основная задача звукопровода состояла в разнесении во времени задержанного сигнала от сигнала прямой электромагнитной наводки с целью предотвращения перегрузки приемного тракта.

В большинстве экспериментов использовались импульсы длительностью 0.3 мкс, при этом собственное время задержки первого проходящего импульса на поперечной волне составляло от 2 до 4 мкс, а полное время задержки с учетом звукопровода – до 25 мкс.

Катушка, применявшаяся для электромагнитного возбуждения ультразвука, выполнялась из медного провода диаметром 0.15 мм, количество витков – порядка 20 – 30, диаметр катушки – около 7 – 10 мм, выбирался таким, чтобы она достаточно плотно надевалась на образец. Катушка являлась частью резонансного контура, настроенного на рабочую частоту 18.9 МГц, задаваемую резонансной частотой пьезопреобразователей.

1.2. Характеристики образцов

В работе исследовались три группы образцов из поликристаллического железоиттриевого граната с различным содержанием алюминия. В образцах первой группы (далее А) содержание алюминия составляло 0.30, что обеспечивало намагниченность 1210 Гс, в образцах второй группы (далее В) эти цифры равнялись 0.70 и 650 Гс, в образцах третьей (далее С) – 1.50 и 210 Гс. Образцы были выполнены в виде прямоугольных параллелепипедов длиной от 9 до 15 мм с поперечными размерами от 3.5 до 4.9 мм. Для обеспечения хорошего акустического контакта торцы образцов полировались алмазной пастой с размером зерна 0.01 мм.

Для экспериментов из каждой группы образцов было выбрано по одному, проявлявшему характерные для группы свойства в наиболее сильной степени. При этом размеры образца группы А составляли , группы В – , группы С – .

Размагничивающие факторы и соответственно размагничивающие поля образцов в предположении однородности рассчитывались по методике, описанной в [39-41], с помощью калибровочных кривых, приведенных в [42]. При этом образец рассматривался как приближающийся по форме к эллипсоиду, где в качестве полуосей эллипсоида брались половинные размеры образца по трем его осям.

Параметры и характеристики образцов приведены в таблице №1.

Таблица №1.

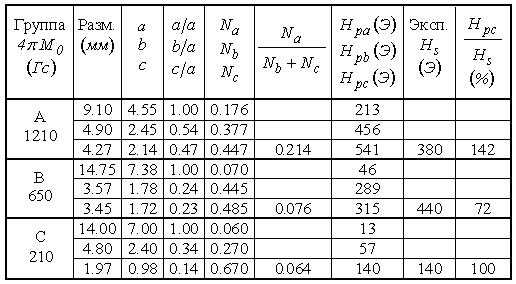
В первом столбце таблицы приведено наименование группы и намагниченность насыщения образца. Во втором – его размеры. В третьем – параметры (полуоси) эквивалентного эллипсоида. В четвертом – полуоси эллипсоида, нормированные на наибольшую из них. В пятом – размагничивающие факторы, нормированные на намагниченность. В шестом – отношение наименьшего размагничивающего фактора к полусумме двух других, определяющее близость формы образца к длинному цилиндру, для которого это отношение стремится к нулю. В седьмом – размагничивающие поля, соответствующие осям эллипсоида. В восьмом – полученное из эксперимента по зависимости затухания от поля значение поля стабилизации затухания , соответствующее выходу зависимости на плоский горизонтальный участок (пояснено далее). В последнем столбце приведено отношение размагничивающего поля вдоль длинной оси образца к полю стабилизации затухания , выраженное в процентах.

Из соотношения размагничивающих факторов образцов можно видеть, что образец С по форме наиболее близко подходит к длинному цилиндру, однако по размагничивающим полям, для цилиндра с намагниченностью равным , , , отличие остается довольно значительным.

Полученные в эксперименте значения поля близки по величине к размагничивающим полям вдоль оси . Расчетные значения в среднем по трем образцам составляют от экспериментальных, то есть различие между теорией и экспериментом в среднем составляет .

Таким образом, учитывая заметное отличие формы образцов от эллипсоидальной, можно полагать, что теория, касающаяся полей размагничивания, описывает эксперимент достаточно адекватно.

1.3. Методика измерений

В экспериментах измерялась амплитуда и время задержки импульсов, проходящих через образец. Схема наблюдения сигналов на экране осциллографа показана на рис.2.

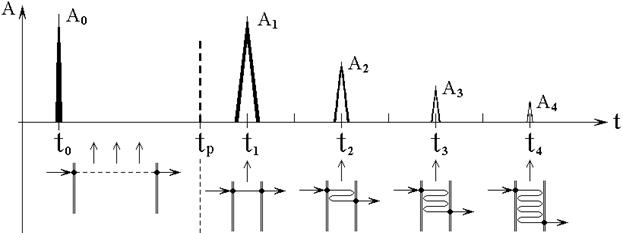
Рис.2. Схема наблюдения сигналов на экране осциллографа.

Наблюдалась серия импульсов в моменты времени , , и так далее. Обычно наблюдались 3-4 импульса, в некоторых экспериментах – до 5 и более.

Возбуждение осуществлялось в момент времени , чему на экране соответствовал импульс наводки с амплитудой .

Промежуток времени от до соответствует распространению упругой волны в звукопроводе, использовавшемся только при электромагнитном возбуждении (рис.1б). При механическом возбуждении (рис.1а) звукопровод и соответственно этот промежуток времени отсутствовал, то есть выполнялось соотношение .

Промежуток времени от до определялся временем прохождения упругой волны через образец. Это промежуток связан со скоростью волны в образце соотношением:

, (1)

где – длина образца, – скорость поперечной упругой волны в образце.

Импульс в момент времени определялся однократным прохождением волны через образец. После такого прохождения волна отражалась от дальнего конца образца, проходила образец в обратном направлении и снова, отражаясь от его начала, проходила образец еще раз, давая импульс в момент времени . Таким образом, импульс в момент времени по сравнению с начальным моментом определялся трехкратным прохождением волны через образец. Дальнейшие импульсы в моменты , и так далее определялись многократным прохождением волны через образец с последовательным переотражением. Схема переотражений показана на рис.2 внизу.

Таким образом, момент времени , где – номер импульса, был связан с начальным моментом времени соотношением:

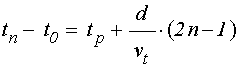, (2)

что позволяло в экспериментах определить скорость упругой волны с помощью соотношения:

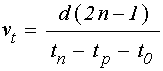. (3)

Интервал времени между соседними импульсами при равнялся:

. (4)

Амплитуда переотраженных импульсов по мере увеличения номера убывала в соответствии с законом:

, (5)

где – начальная амплитуда, соответствующая моменту начала возбуждения волны , – параметр затухания волны, определяемый как коэффициент при времени в отрицательном показателе экспоненты.

Однако амплитуда в эксперименте не определена, поэтому удобнее отсчитывать время от момента , для которого получаем:

. (6)

При этом параметр затухания, определяется соотношением:

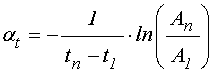, (7)

которое для двух соседних импульсов приобретает вид:

, (8)

или с учетом (4):

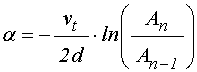. (9)

В экспериментах амплитуда импульсов измерялась по напряжению, поэтому параметр затухания было удобно измерять в децибелах на секунду:

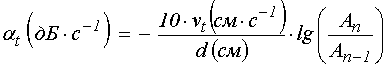. (10)

Учитывая, что волна за одну секунду проходит расстояние, равное скорости , затухание волны удобно было измерять в децибелах на сантиметр:

, (11)

где параметры и связаны соотношением:

. (12)

Таким образом, если требовалось узнать, насколько уменьшилась амплитуда волны за определенный промежуток времени, то надо было пользоваться параметром , а для того, чтобы узнать, насколько уменьшилась амплитуда при прохождении определенного расстояния, надо было пользоваться параметром .

2. Основные предметы исследования

Основными предметами экспериментального исследования в настоящей работе являлись следующие:

1) зависимость затухания упругих волн, возбуждаемых пьезопреобразователем, от величины магнитного поля при поперечном намагничивании;

2) зависимость затухания упругих волн, возбуждаемых пьезопреобразователем, от величины магнитного поля при продольном намагничивании;

3) зависимость амплитуды упругих волн, возбуждаемых катушкой, от величины магнитного поля при поперечном намагничивании.

Приведенное далее рассмотрение является первой частью работы в целом и содержит результаты исследования затухания только при поперечном намагничивании. Двум другим вопросам – продольному намагничиванию и электромагнитному возбуждению будут посвящены последующие части работы.

3. Экспериментальные результаты исследования затухания упругой волны при поперечном намагничивании

Рассмотрим результаты экспериментального исследования затухания упругой волны при поперечном намагничивании, для чего обратимся к рис.3.

На этом рисунке показаны зависимости затухания ультразвуковых импульсов от поля при намагничивании образца по нормали к направлению распространения волны, то есть поперек его длинной оси. При изменении поля измерялся коэффициент затухания в децибелах на сантиметр, то есть параметр по (11), после чего полученные значения нормировались на тот же параметр затухания в отсутствие поля.

Рис.3. Зависимости нормированной величины параметра затухания от поля при поперечном намагничивании образца.

А, В, С – наименования серий образцов.

Из рисунка видно, что для образцов серий А и С затухание с увеличением поля от нуля сразу довольно резко уменьшалось. Для образца серии В сначала наблюдался небольшой (~7%) рост затухания, после чего оно также уменьшалось. Для всех образцов уменьшение затухания при некотором поле, которое будем обозначать через , прекращалось и зависимость затухания от поля выходила на горизонтальный участок. Для образца А поле равнялось 380 Э, для образца В – 440 Э, для образца С – 140 Э. Эти же значения приведены в таблице №1 раздела 1.2, где показано, что они довольно хорошо коррелируют со значениями размагничивающего поля вдоль длинной оси образца.

4. Теоретическая интерпретация наблюдаемых явлений. Общие положения

Рассмотрим теперь теоретическую интерпретацию наблюдаемых явлений. Сначала введем общие положения, после чего будем следовать порядку изложения описанных в предыдущем разделе экспериментальных результатов.

4.1. Общая геометрия задачи

Общая геометрия задачи иллюстрируется рис.4.

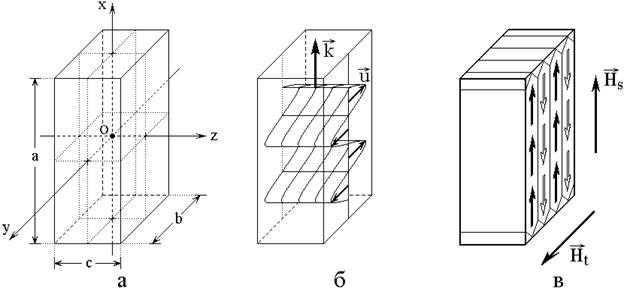
Рис.4. Общая геометрия задачи.

а – образец и система координат; б – поперечная волна; в – доменная структура.

На рис.4а показан общий вид и ориентация системы координат относительно образца. Образец имеет форму прямоугольного параллелепипеда с размерами ребер , , , такими, что . Начало декартовой системы координат , точка , располагается в геометрическом центре образца. Ось параллельна ребру , ось – ребру , ось – ребру . Такой выбор является традиционным при расчете поля внутри эллипсоида [39-42]. Размагничивающие поля внутри образца рассчитывались именно исходя из его размеров , , так, как если бы образец имел форму эллипсоида.

На рис.4б показана схема распространения поперечной упругой волны в образце. Волновой вектор волны, совпадающий с направлением ее распространения, параллелен оси , упругое смещение – параллельно оси .

На рис.4в показана схема доменной структуры в образце в размагниченном состоянии. Основные домены, занимающие преобладающую часть образца, имеют вид прямых полос и вытянуты вдоль его длинного размера, параллельно оси .

Векторы намагниченности внутри этих доменов (показаны стрелками) ориентированы также вдоль оси и в соседствующих доменах антипараллельны.

Вблизи торцов образца, параллельных плоскости , имеются небольшие треугольные замыкающие домены, векторы намагниченности в которых ориентированы перпендикулярно намагниченности основных доменов, то есть параллельно плоскости (на рисунке эти векторы не обозначены ввиду их маловажности).

В экспериментах внешнее поле прикладывалось перпендикулярно или параллельно длинному размеру образца, вдоль ребер или . На рис.4в поле вдоль ребра , то есть оси , обозначено как , а вдоль ребра , то есть оси – как .

4.2. Общий размагничивающий фактор

По размерам и размещается много доменов. Можно полагать, что домены имеют вид длинных вытянутых вдоль длины образца прямоугольных параллелепипедов с квадратным поперечным сечением.

Если бы соседних доменов не было, плотность магнитной энергии одного домена бесконечной длины имела бы вид:

, (13)

где – составляющие вектора намагниченности внутри этого домена.

Теперь рассмотрим полную совокупность доменов в образце. Схема поворота векторов намагниченности в доменах разных знаков при поперечном намагничивании образца показана на рис.5.

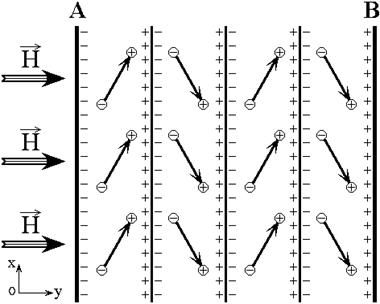
Рис.5. Схема поворота векторов намагниченности в доменах разных знаков.

В отсутствие внешнего поля векторы намагниченности в соседних доменах ориентированы вдоль оси в двух взаимно противоположных направлениях – положительном и отрицательном.

При воздействии поля вдоль оси векторы намагниченности во всех доменах поворачиваются к направлению поля. При этом на границах между доменами появляются магнитные заряды противоположных знаков, которые взаимно компенсируются. Нескомпенсированными остаются только заряды на внешних границах образца А и В. Таким образом, составляющие векторов намагниченности, направленные вдоль поля, складываются, в результате чего в этом направлении возникает суммарная составляющая намагниченности. В силу равенства намагниченностей соседних доменов, заряды, возникающие на противоположных сторонах каждой границы, между собой равны, поэтому составляющая намагниченности переходит из домена в домен непрерывным образом. В результате непрерывности такой составляющей, на ее величине сказываются только границы образца, за которыми домены уже отсутствуют. Здесь возникает размагничивающее поле, определяемое величиной этой суммарной составляющей вектора намагниченности. Таким образом, в результате компенсации зарядов на внутренних границах доменов, суммарная намагниченность ведет себя так, как если бы доменов не было, то есть размагничивающие факторы в этом случае определяются формой не домена, а образца в целом.

При этом плотность магнитной энергии размагничивания доля образца в целом принимает вид:

. (14)

где – составляющие вектора намагниченности внутри доменов, , , – размагничивающие факторы образца в целом относительно осей , , .

4.3. Ориентационный переход

Будем рассматривать намагничивание образца полем, перпендикулярным его длинному размеру.

В размагниченном состоянии векторы намагниченности в доменах ориентированы вдоль длинного размера образца в двух взаимно противоположных направлениях. При увеличении поля векторы намагниченности поворачиваются к его направлению, образуя с ним равные углы того и другого знака. При этом составляющие векторов намагниченности внутри доменов вдоль длинного размера образца уменьшаются, но всегда остаются равными друг другу, различаясь лишь по знаку. Таким образом, поперечные размеры доменов обоих знаков остаются равными друг другу, а внутри каждого домена происходит ориентационный переход вектора намагниченности к направлению поля.

Схема поворота векторов намагниченности при ориентационном переходе внутри доменов разных знаков иллюстрируется на рис.6.

На рис.6а показана ориентация векторов намагниченности в отсутствие поля. Ориентационный переход еще не начинался. В этом случае векторы намагниченности и имеют взаимно противоположные ориентации в положительном и отрицательном направлениях оси .

Рис.6б соответствует включению поля вдоль оси , величина которого меньшего (получена далее). Ориентационный переход находится в процессе совершения. Векторы намагниченности отклонены от оси к направлению поля под равными углами противоположных знаков. Имеется суммарная составляющая намагниченности вдоль оси , тогда как подобная составляющая вдоль оси отсутствует.

Рис.6в соответствует полю, большему . Ориентационный переход закончился. Векторы намагниченности во всем образце полностью повернуты вдоль поля параллельно оси , составляющая намагниченности вдоль оси отсутствует.

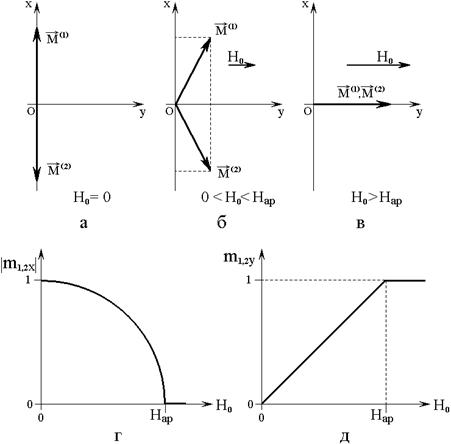
Рис.6. Схема ориентационного перехода в доменах разных знаков.

а, б, в – ориентация векторов намагниченности;

г, д – зависимости нормированных компонент намагниченности от поля.

На рис.6г и 6д показаны зависимости нормированных компонент намагниченности от поля. Можно видеть, что компоненты в процессе перехода уменьшаются от единицы до нуля по выгнутой вверх выпуклой кривой. Компоненты в процессе того же перехода увеличиваются от нуля до единицы по линейному закону. Переход заканчивается при поле , когда составляющие намагниченности равны: , .

4.4. Поворот намагниченности при ориентационном переходе

Рассмотрим поворот вектора намагниченности при ориентационном переходе более подробно, исходя из плотности энергии образца при намагничивании поперечным полем.

Плотность энергии магнетика в поле в общем случае равна [43,44]:

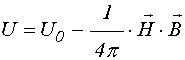, (15)

где – плотность энергии, не связанная с намагниченностью, а магнитная индукция равна:

. (16)

Подставляя (16) в (15), получаем:

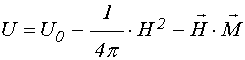. (17)

Опуская слагаемые, не связанные с намагниченностью, получаем плотность энергии магнетика во внешнем поле (записываем в обозначениях [43]):

. (18)

Аналогично плотность энергии размагничивающего поля равна:

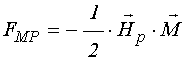. (19)

Получение в этом выражении коэффициента подробно объяснено в [43],

поэтому далее примем этот коэффициент как данное.

При малом отличии формы образца от эллипсоидальной, можно пользоваться выражением для размагничивающего поля в виде:

, (20)

где не зависит от и является в общем случае тензором второго порядка – тензором размагничивающего фактора. В этом случае (19) принимает вид:

. (21)

Для эллипсоида при , то есть:

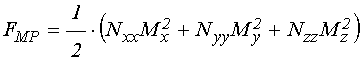. (22)

При этом:

. (23)

Введем обозначения, аналогичные принятым в [40,41]:

; (24)

; (25)

. (26)

В этих обозначениях:

. (27)

Введем также нормированную намагниченность:

. (28)

При этом из (18) и (21) получаем:

; (29)

. (30)

Полная плотность энергии принимает вид:

. (31)

Согласно общей геометрии рассматриваемой задачи положим, что вектор намагниченности находится в плоскости , а поле направлено вдоль оси , то есть:

; (32)

. (33)

При этом полная плотность энергии (31) принимает вид:

. (34)

Из условия сохранения длины вектора намагниченности:

, (35)

получаем:

. (36)

Подставляя (36) в (34), получаем:

. (37)

Последнее слагаемое является постоянной величиной, поэтому его можно опустить. В результате получаем:

. (38)

Найдем равновесное положение вектора намагниченности из условия равенства нулю первой производной:

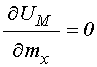. (39)

Дифференцируя (38), получаем:

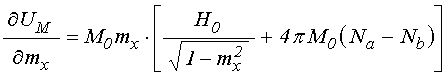. (40)

В соответствии с (39) получаем уравнение для :

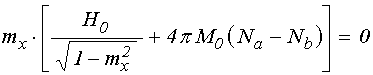. (41)

Вообще говоря, это уравнение имеет несколько решений, то есть зависимость от имеет несколько экстремумов. Являются ли они максимумами или минимумами, надо проверять по знаку второй производной. Однако и так ясно, что решение дает максимум, поэтому рассмотрим другие возможности.

При , получаем уравнение:

. (42)

Учитывая, что , то есть , в скобках можно поменять местами слагаемые с изменением знака перед скобкой. Далее, перенося второе слагаемое в правую часть, возводя в квадрат и выделяя , получаем:

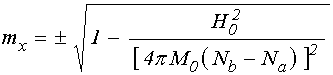. (43)

Здесь знаки соответствуют намагниченности в различных доменах.

В полученном выражении величина эквивалентна полю анизотропии, получающемуся за счет формы образца. Назовем его «полем анизотропии формы» и введем обозначение:

. (44)

Здесь индекс «» соответствует анизотропии, а индекс «» показывает, что эта анизотропия обусловлена размагничиванием.

Подставляя это обозначение в (43), получаем:

. (45)

Найдем из условия сохранения длины вектора намагниченности (35), а также учтем, что ориентировано в положительном направлении оси :

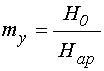. (46)

Построенные по этим формулам зависимости нормированных компонент намагниченности и от поля показаны на рис.6г и 6д соответственно.

5. Затухание упругой волны при ориентационном переходе

Рассмотрим теперь затухание упругой волны при ориентационном переходе более подробно.

5.1. Взаимодействие поля волны с намагниченностью в доменах

Будем полагать, что в размагниченном состоянии образец разбит на домены, выстроенные, благодаря действию размагничивания, вдоль его длинной оси. При этом векторы намагниченности внутри доменов в своем равновесном положении также ориентированы вдоль той же оси, причем в соседствующих доменах векторы намагниченности ориентированы противоположно.

При распространении упругой волны в таком образце, вследствие ее поперечного характера, упругое смещение ориентировано перпендикулярно направлению распространения, то есть направлению намагниченности.

При этом поля магнитострикции, будучи направленными вдоль упругого смещения, то есть перпендикулярно намагниченности, стремятся повернуть векторы намагниченности перпендикулярно направлению их равновесного положения.

Такой поворот требует от упругой волны определенной затраты энергии, вследствие чего волна по мере распространения свою энергию теряет, ее амплитуда уменьшается, то есть волна претерпевает затухание.

При приложении постоянного поля, перпендикулярного длинной оси образца, векторы намагниченности внутри доменов разворачиваются к направлению поля тем сильнее, чем поле больше. При этом, благодаря перпендикулярности поля равновесной оси ориентации намагниченности, размер доменов меняется мало, только за счет уменьшения энергии границ, то есть домены слегка увеличиваются, но периодичность чередования намагниченности сохраняется. Таким образом, внутри доменов происходят как бы симметричные ориентационные переходы намагниченности к направлению поля [45]. При таком ориентационном переходе компонента намагниченности, параллельная оси образца, уменьшается, вследствие чего ее взаимодействие с поперечным полем магнитострикции волны уменьшается, так что потери энергии волны и ее затухание также уменьшаются.

Такое уменьшение затухания прекращается тогда, когда векторы намагниченности в доменах полностью ориентируются вдоль поля, то есть ориентационный переход заканчивается.

Из теории ориентационных переходов в том числе с доменами [46,47] известно, что переход заканчивается при поле, близком к полю анизотропии (точнее – незначительно, на единицы процентов, его превышающем). В настоящем случае образцы являются поликристаллами, то есть кристаллографическая анизотропия у них отсутствует, поэтому роль анизотропии играет анизотропия формы образца. Поле такой анизотропии равно полю размагничивания, в результате чего ориентационный переход, а с ним и затухание упругой волны за счет взаимодействия с намагниченностью, прекращается как раз при поле, равном полю размагничивания. Этим объясняется прекращение падения затухания и выход кривых на рис.3 на горизонтальный участок.

Такой выход происходит при поле , значения которого для исследованных образцов приведены в таблице №1. Рассмотрим соотношение этого поля с полем , определяемым формулой (44), соответствующим окончанию ориентационного перехода, для чего обратимся к таблице №2.

Таблица №2.

В первом столбце таблицы приведено наименование группы и намагниченность насыщения образца. Во втором – значения поля , полученного из эксперимента. В третьем – величина поля , рассчитанная с помощью данных таблицы №1 по формуле (44).

Из сравнения второго и третьего столбцов видно, что экспериментальное значение поля окончания уменьшения затухания заметно превышает расчетное значение поля окончания ориентационного перехода . То есть, если полагать, что окончание уменьшения затухания соответствует окончанию ориентационного перехода, то можно сделать вывод, что ориентационный переход как бы «затягивается» в строну больших полей.

В четвертом столбце приведено отношение этих двух полей , характеризующее превышение экспериментального значения над расчетным, то есть затягивание ориентационного перехода. Можно полагать, что такое затягивание обусловлено отличием формы образца от эллипсоидальной или точнее – сферической. Для оценки такого отличия в пятом столбце приведено отношение наименьшего размера образца к наибольшему , полученное на основе данных, приведенных в таблице №1. Для сферы такое отношение было бы равным единице, здесь же оно еще довольно велико для наиболее короткого образца А () и совсем мало для наиболее длинного образца С (). Таким образом, степень затягивания с увеличением отличия формы образца от сферы действительно увеличивается.

В последнем шестом столбце таблицы приведено произведение отношения полей на отношение размеров . Можно видеть, что значения такого произведения для разных образцов близки друг к другу и отличаются от среднего значения примерно на . То есть в этом случае, учитывая сложность строения доменной структуры, согласие теории с экспериментом, в предположении затягивания ориентационного перехода, можно считать удовлетворительным.

5.2. Механизм затягивания ориентационного перехода

Однако остается открытым вопрос о качественной физической причине затягивания ориентационного перехода.

Для иллюстрации такого явления обратимся к рис.7, где схематически показана конфигурация доменной структуры в отсутствие внешнего поля (а) и при его наличии (б).

Рис.7а соответствует отсутствию поля. В этом случае основную часть образца занимают домены, в которых векторы намагниченности ориентированы вдоль длинного размера образца, параллельного координатной оси . Вблизи поверхности образца имеются замыкающие домены, в которых векторы намагниченности ориентированы вдоль оси . Магнитные заряды, обусловленные выходом векторов намагниченности замыкающих доменов на их поверхности, образуют поля и , составляющие которых вдоль оси в пределах основных доменов принимают два направления – положительное и отрицательное. В силу равенства объемов замыкающих доменов разных знаков, поля и также равны по величине, а благодаря их разным знакам, взаимно компенсируются, не оказывая заметного влияния на ориентацию намагниченности основных доменов.

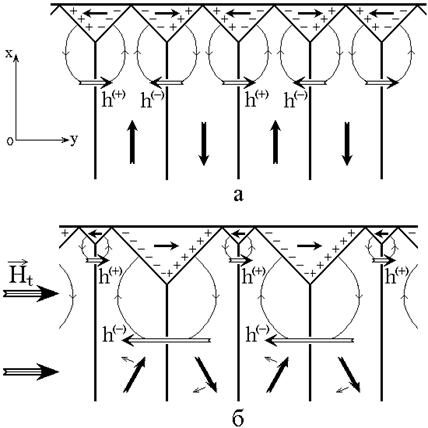
Рис.7. Схема образования полей замыкающих доменов. Плюсы и минусы – магнитные заряды на поверхностях замыкающих доменов. Сплошные стрелки – векторы намагниченности в доменах. Открытые стрелки – поля магнитных зарядов доменов. Тонкие линии – силовые линии полей доменов.

Ситуация, соответствующая включению внешнего поля вдоль положительного направления оси , вызывающего ориентационный переход, иллюстрируется рис.7б. Здесь равенство объемов замыкающих доменов нарушается в тем большей степени, чем внешнее поле больше.

Увеличиваются в размере те замыкающие домены, вектор намагниченности в которых ориентирован вдоль поля , тогда как домены противоположного знака в объеме уменьшаются. В результате на поверхностях увеличивающихся доменов сосредотачивается большее число магнитных зарядов, что приводит к увеличению поля , тогда как поле уменьшается.

При достаточном увеличении поля поле может значительно превысить поле , в результате чего его роль в воздействии на векторы намагниченности в основных доменах становится преобладающей.

Поле направлено противоположно внешнему полю , в результате чего поворачивающее действие поля на векторы намагниченности в основных доменах уменьшается. Так, если поле стремится повернуть векторы намагниченности к своему направлению, то поле отворачивает их от этого направления, как это показано маленькими стрелками около этих векторов.

Таким образом, для полного выстраивания векторов намагниченности в основных доменах вдоль оси , то есть для завершения ориентационного перехода, требуется значительно большие значения поля , чем это было бы в отсутствие замыкающих доменов.

Такое увеличение поля и является причиной «затягивания» ориентационного перехода.

5.3. Оценка степени затягивания ориентационного перехода

Оценим степень затягивания ориентационного перехода количественно. Для точной оценки необходимо знать конкретное устройство доменной структуры образца, которая в случае прямоугольного параллелепипеда может быть весьма сложной. Однако непосредственные эксперименты на образцах, имеющих форму достаточно широких пластин [43], показывают, что большую часть объема образца занимают домены в виде плоскопараллельных слоев, а вблизи торцевых поверхностей присутствуют треугольные замыкающие домены. То есть реальная структура с весьма хорошим приближением описывается изображенной на рис.7 моделью.

В экспериментах, описанных в разделе 3, ширина доменов не измерялась, поэтому воспользуемся для ее оценки формулой для «характеристической длины», определяющей порядок ширины домена в теории материалов с цилиндрическими магнитными доменами (ЦМД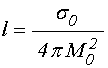) [47]:

, (47)

где – поверхностная плотность энергии доменной границы, для границы блоховского типа в материале с одноосной анизотропией определяемая соотношением [43]:

, (48)

где – константа анизотропии, – константа неоднородного обменного взаимодействия, – постоянная решетки кристалла.

В нашем случае вместо одноосной анизотропии присутствует анизотропия формы, а конфигурация доменов в исследуемом материале, поликристаллическом ЖИГ, существенно отличается от ЦМД. Поэтому непосредственное использование формул (47)-(48) невозможно. Предположим однако, что зависимость ширины доменов от намагниченности, подобно (47), обратно пропорциональна квадрату намагниченности , то есть будем полагать:

, (49)

где коэффициент определим из экспериментов по пленкам ЖИГ. Так в работах [26,27,48,49] для пленок ЖИГ, где нормальная анизотропия мала («второго типа» по принятой там терминологии), размер доменов составляет порядка . При этом, полагая для ЖИГ [40,41], получаем: . Пользуясь этим значением, будем оценивать размеры доменов в исследуемых образцах с помощью формулы (49).

Далее будем полагать, что поле проявляет себя в качестве причины затягивания ориентационного перехода на расстоянии от поверхности образца в два раза превышающем ширину домена , то есть:

. (50)

Такое предположение правдоподобно в том плане, что это поле может заметно проявляться только на глубине, куда проникают замыкающие домены, которая, как можно видеть из геометрии на рис.7б, даже при полном исчезновении доменов невыгодного знака, равняется ширине основных доменов . Это условие выполняется в предположении, что ширина основных доменов с полем не меняется, а стенки замыкающих доменов всегда составляют со стенками основных доменов угол в . Регистрация поля на расстоянии приближенно отражает усредненный от нуля до бесконечности спад этого поля по мере углубления внутрь образца.

Полученные результаты сведены в таблицу №3.

Таблица №3.

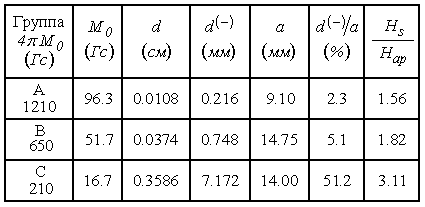
В первом столбце таблицы приведено наименование группы и намагниченность насыщения образца. Во втором – намагниченность насыщения без коэффициента . В третьем – ширина доменов, определенная по формуле (49). В четвертом – параметр , определяемый соотношением (50), выраженный в миллиметрах для удобства сравнения с размерами образца. В пятом – размер образца вдоль оси , аналогичный приведенному в таблице №1. В шестом – отношение в процентах, характеризующее глубину проникновения поля в толщу образца. И наконец в седьмом – отношение экспериментального значения поля окончания ориентационного перехода к расчетному , характеризующее величину затягивания перехода.

Из сопоставления численных значений, приведенных в шестом и седьмом столбцах, можно видеть, что по мере увеличения глубины проникновения поля в толщу образца, величина затягивания поля перехода также увеличивается. Такое соответствие говорит в пользу предложенной модели затягивания за счет влияния замыкающих доменов.

Следует однако заметить, что прямая пропорциональность между этими двумя величинами отсутствует. Так например при увеличении глубины проникновения примерно в два раза (переход от образца А к образцу В) затягивание перехода увеличивается в 1.17 раз (), тогда как при дальнейшем увеличении глубины в 10 раз, то есть в пять раз больше (переход от образца В к образцу С), затягивание перехода увеличивается всего в 1.71 раза (). Можно полагать, что столь неравномерное увеличение затягивания по мере увеличения глубины проникновения обусловлено более сложным, чем здесь рассмотренный, характером доменной структуры образцов.

5.4. Два фактора затягивания

Из рассмотрения таблицы №3 и приведенных оценок можно видеть, что сильное затягивание поля перехода в образце С по сравнению с затягиванием в образцах А и В обусловлено значительно большим размером доменов в этом образце, чем в двух других. Такое увеличение размера доменов, в свою очередь, обусловлено малостью намагниченности этого образца.

С другой стороны, в разделе 5.1 было показано, что затягивание проявляется тем сильнее, чем больше форма образца отличается от сферической.

Таким образом, резюмируя сказанное, в качестве факторов, обусловливающих затягивание ориентационного перехода, можно выделить два: отличие формы образца от сферической и малость его намагниченности насыщения.

6. Механизмы затухания упругой волны в доменах

Рассмотрим теперь зависимость затухания упругой волны от поперечного поля более подробно. В качестве возможных механизмов будем полагать взаимодействие упругой волны с намагниченностью за счет магнитострикции, а также возбуждение обменных спиновых волн на неоднородной доменной структуре. Рассмотрим эти механизмы последовательно.

6.1. Взаимодействие поля волны с намагниченностью

В качестве первого фактора, обусловливающего затухание упругой волны, рассмотрим воздействие поля волны на намагниченность в доменах через посредство магнитострикции.

Плотность энергии магнитоупругого взаимодействия сдвиговых компонент тензора деформаций с намагниченностью имеет вид [2]:

, (51)

где – константа магнитоупругого взаимодействия, – тензор деформаций, равный [50]:

. (52)

В рассматриваемой геометрии сдвиговая поперечная упругая волна распространяется вдоль оси , причем упругое смещение в этой волне направлено вдоль оси . Таким образом, в выражении (52) отлична от нуля только одна производная , поэтому плотность энергии (51) принимает вид:

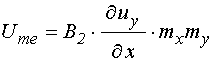. (53)

При распространении вдоль оси поперечная упругая волна возбуждает магнитное поле, направленное вдоль оси . Такое поле раскачивает векторы намагниченности в доменах, на что требуется определенная энергия, которую оно забирает от упругой волны, обеспечивая тем самым ее затухание.

В соответствии с общим термодинамическим определением эффективного поля из плотности энергии [40,41], из (53) получаем:

. (54)

Поскольку именно это поле взаимодействует с намагниченностью в доменах, можно полагать, что величина затухания упругой волны прямо пропорциональна компоненте намагниченности , определяемой соотношением (45), откуда получаем:

. (55)

6.1. Возбуждение обменных волн

Другим фактором, дополняющим затухание упругой волны, может быть возбуждение обменных спиновых волн, уносящих часть энергии упругой волны, чем усиливающих ее затухание. Рассмотрим возможный механизм возбуждения таких волн.

Как известно [40,41,51], для возбуждения обменных волн динамической намагниченностью достаточно наличия неоднородности распределения намагниченности с характерным размером, порядка длины таких волн. Рассмотренная в упомянутых работах неоднородность намагниченности обусловлена дефектами структуры образца. В поликристаллическом образце такими дефектами являются границы зерен отдельных кристаллитов, частично рассмотренные в тех же работах. Однако такие неоднородности не зависят от приложенного внешнего магнитного поля, поэтому могут обеспечить затухание упругих волн, в основном, на горизонтальном участке кривых, приведенных на рис.3.

Источником неоднородности намагниченности, зависящим от поля, может явиться доменная структура, за счет которой могут возбуждаться обменные волны той же длины, что и размер доменов [52-54]. На возбуждение этих волн расходуется энергия, что приводит к потерям энергии упругой волны и ее дополнительному затуханию. Неоднородность намагниченности вдоль поля является динамической, меняющейся с частотой упругой волны. Неоднородность намагниченности поперек поля обусловлена доменной структурой и является статической. Поэтому неоднородность намагниченности, продольная относительно поля, может возбуждать спиновую волну в силу своего динамического характера, а поперечная, будучи статической, спиновые волны не возбуждает.

Таким образом, к потерям энергии упругой волны приводит только неоднородная составляющая намагниченности, направленная вдоль поля.

Возбуждаемая спиновая волна имеет частоту упругой волны, а распределение намагниченности – периодическое, определяемое периодом доменов.

Можно предполагать, что размер домена с увеличением поля увеличивается. Это может быть обусловлено тем, что в результате поворота векторов намагниченности внутри доменов к направлению поля, энергия доменных границ уменьшается, так как углы между векторами намагниченности в соседних доменах становятся меньше развернутого угла и в поле перехода стремятся к нулю. Однако при этом и компоненты намагниченности, перпендикулярные полю, уменьшаются, так что увеличение размеров доменов будет не столь большим. Если все же полагать, что размер доменов при увеличении поля увеличивается, то это означает, что длина возбуждаемой спиновой волны тоже увеличивается, то есть ее энергия уменьшается. В этом случае потери упругой волны за счет такого возбуждения, также с увеличением поля уменьшаются.

Заметим, что увеличение размеров доменов с полем является бесспорным вблизи окончания ориентационного перехода, где домены вообще исчезают, то есть их размеры увеличиваются до размеров образца в целом.

Поскольку зависимость размеров доменов от поля требует отдельного рассмотрения и выходит за рамки настоящей работы, будем приближенно считать, что размер доменов обратно пропорционален компоненте намагниченности , перпендикулярной полю , определяемой соотношением (45), то есть:

. (56)

Положим далее, что возбуждаемая за счет неоднородности намагниченности в доменах обменная спиновая волна имеет ту же длину, то есть:

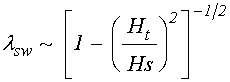. (57)

При этом ее волновое число определяется соотношением:

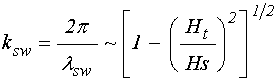. (58)

Положим теперь, что коэффициент затухания упругой волны пропорционален энергии возбуждаемой обменной волны, которая в свою очередь пропорциональна квадрату ее волнового числа, что следует из квадратичного закона дисперсии обменных волн [40,41]:

. (59)

6.3. Суммарный механизм затухания

Будем полагать далее, что полные потери уменьшаются пропорционально произведению фактора потерь (55), определяемого продольной составляющей намагниченности (45), на коэффициент, обусловленный возбуждением спиновых волн вида (59), то есть

. (60)

Рассмотрим далее, в какой степени представленные механизмы затухания обеспечивают теоретическую интерпретацию экспериментальных результатов.

7. Сравнение механизмов затухания с экспериментом

Результаты общей оценки затухания упругой волны в соответствии с двумя описанными механизмами, иллюстрируются рис.8, где показаны дважды нормированные зависимости затухания упругой волны от внешнего поля при поперечном намагничивании.

Приведенные на этом рисунке экспериментальные зависимости получены из подобных зависимостей на рис.3 с помощью нормировки по двум осям. По вертикальной оси для этого сначала из полной величины затухания, приведенной на рис.3, вычиталась величина затухания, соответствующая горизонтальному участку экспериментальных кривых, после чего начала кривых, соответствующие , приводились к единице. По горизонтальной оси значения поля нормировались на поле начала горизонтального участка .

Целью такой процедуры являлось выделение механизма затухания, связанного с доменами, в чистом виде, а также приведение зависимостей для образцов с различными параметрами к единому масштабированию.

Таким образом, экспериментальные точки на рис.8 соответствуют приведенным на рис.3. Приведенные на рис.8 непрерывные кривые соответствуют рассмотренным здесь модельным положениям. Так кривая 1 построена по формуле (55), 2 – по формуле (59), 3 – по формуле (60).

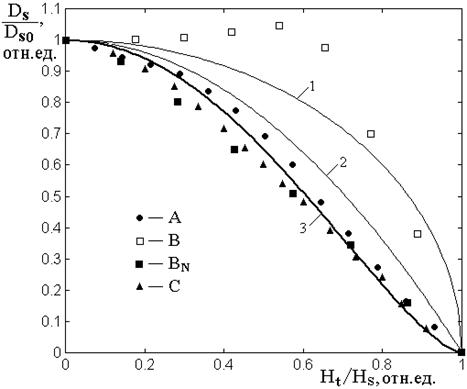
Рис.8. Дважды нормированная зависимость затухания упругой волны от внешнего поля при поперечном намагничивании.

Сплошные линии – теория, точки – эксперимент.

А, В, С – наименования серий образцов.

1 – формула (55), 2 – (59), 3 – (60).

Из рисунка видно, что предложенная интерпретация (60) превосходно (с точностью не хуже 5%) описывает экспериментальные результаты для образцов A и C, что говорит в пользу адекватности теоретических положений.

Для образца B спад экспериментальных точек (квадраты с открытой серединой) по мере увеличения поля наблюдается в достаточной степени, что говорит в пользу рассмотренного механизма ориентационного перехода. С другой стороны, сильное (до полутора-двух раз) превышение экспериментальных точек над теоретической кривой, особенно ярко проявляющееся в полях от 0.4 до 0.7 относительных единиц говорит, во-первых, о слабости механизма возбуждения обменных волн в этом образце и, во-вторых, о наличии какого-то иного неучтенного механизма. В качестве такого механизма можно предположить более сложный характер доменной структуры, при котором перестройка доменов при ориентационном переходе происходит не от нулевого положения векторов намагниченности, а от каких-то заранее заданных других направлений, возможно связанных с текстурой или дефектностью образца, что и дает рост затухания в области полей от 0 до 0.6 относительных единиц. Ну а в области полей от 0.6 до 1.0 относительных единиц соответствующая нормировка (сдвиг нуля поля на 0.6) приводит к такому же виду экспериментальной зависимости, что и описанная формулой (60), как это показано точками (квадраты сплошные), что также свидетельствует в пользу предложенных теоретических положений.

Заключение

Выполнено экспериментальное исследование распространения поперечных упругих волн в образцах из поликристаллического железоиттриевого граната, легированного алюминием. Измерения выполнены импульсным методом на установке, работающей в диапазоне 18.9 МГц с длительностью импульса 0.3 мкс. Образцы представляли собой прямоугольные параллелепипеды с размерами от 3 до 15 миллиметров и различными размагничивающими факторами по всем трем осям. Упругие волны распространялись вдоль наиболее длинной оси образца. Возбуждение осуществлялось механическим способом с помощью пьезоэлектрических преобразователей или электромагнитным с помощью катушки, надетой на образец. Прием упругих волн осуществлялся пьезоэлектрическим преобразователем.

Исследовано затухание возбуждаемых механическим способом упругих волн при поперечном намагничивании образца постоянным полем. Показано, что при увеличении поля затухание упругой волны убывает вплоть до поля насыщения образца, где далее не меняется.

Выполнена теоретическая интерпретация наблюдаемых явлений, для чего предложена модель ориентационного перехода векторов намагниченности в доменах без изменения их относительной величины.

Оценен общий размагничивающий фактор образца в целом и установлена его связь с геометрическими размерами как самого образца, так и содержащихся в нем доменов. Построена модель ориентационного перехода намагниченности в доменах на основе минимизации плотности энергии магнитоупругого взаимодействия. Найдено поле окончания ориентационного перехода и его связь с размагничивающими факторами образца.

На основе анализа наблюдаемого в эксперименте затухания упругой волны при ориентационном переходе выявлено явление затягивания перехода, состоящее в значительном (до полутора-двух раз) превышении экспериментального значения перехода по сравнению со значением, полученным из модели размагничивающих факторов.

Для интерпретации явления затягивания перехода предложена модель, состоящая в несимметричном росте полей замыкающих доменов разных знаков, обеспечивающем неэквивалентные условия ориентационных переходов намагниченности в соседствующих доменах основной части образца. Показано, что роль замыкающих доменов проявляется тем сильнее, чем глубже их поля проникают в толщу образца. Установлена связь глубины проникновения с размерами и формой образца, а также его намагниченностью, проявляющаяся через посредство размеров основных доменов. Выполнена численная оценка роли механизма несимметричного роста замыкающих доменов в затягивании ориентационного перехода, выявлено количественное соответствие с экспериментом. В качестве главных факторов, обусловливающих затягивание ориентационного перехода, выделены два: отличие формы образца от сферической и малость его намагниченности насыщения.

Рассмотрены механизмы, обусловливающие затухание упругой волны при ее распространении в образце с доменами. В качестве первого механизма указаны потери энергии волны, связанные с возбуждением колебаний намагниченности за счет магнитного поля волны, возбуждаемого через магнитострикцию. В качестве второго механизма указаны потери энергии волны на возбуждение обменных спиновых волн на неоднородностях образца, обеспечиваемых доменами разных знаков. Показано, что эффективность совокупного действия обоих механизмов пропорциональна составляющей вектора намагниченности, перпендикулярной направлению внешнего поля, в степени три вторых. Выявлена причина уменьшения затухания с увеличением поля, состоящая в уменьшении указанной составляющей намагниченности. Сопоставление предложенной модели с наблюдаемой в эксперименте зависимостью затухания волны от поля показало соответствие теории эксперименту с точностью не хуже 5%.

Экспериментальная часть работы выполнена при финансовой поддержке РФФИ (гранты №12-02-01035-а, №13-02-01401-а).

Теоретическая часть работы выполнена за счет гранта Российского Научного Фонда (проект № 14-22-00279).

Литература

1. Ультразвук. Маленькая энциклопедия. Глав.ред. И.П.Голямина. – М.: Советская энциклопедия. 1979.

2. Физическая акустика. Под ред. Мэзона У., Терстона Р. Т.1-7. М.: Мир. 1966-1974.

3. Такер Дж., Рэмптон В., Гиперзвук в физике твердого тела. М.: Мир. 1975.

4. Поверхностные акустические волны. Под ред. Олинера А. М.: Мир. 1981.

5. Викторов И.А. Звуковые поверхностные волны в твердых телах. М.: Наука. 1981.

6. Bleustein J.L. // Appl. Phys. Lett. 1968. V.13. P.412.

7. Гуляев Ю.В. // ПЖЭТФ. 1969. Т.9. С.63.

8. Кикучи Е. Ультразвуковые преобразователи. М.: Мир. 1972.

9. Ганева Л.И., Голямина И.П. // Акустический журнал. 1974. Т.20. №3. С.378.

10. Гутин Л.Я. Избранные труды. Л.: Наука. 1977.

11. Голямина И.П. // В сб.: Физика и техника мощного ультразвука. Кн.1. Источники мощного ультразвука. М.: Наука. 1967. С.111.

12. Comstock R.L., LeCraw R.C. // J. Appl. Phys. 1963. V.34. № 10. P.3022.

13. Ле-Кроу Р., Комсток Р. // В кн.: У. Мэзон (ред.): Физическая акустика. Т.3Б. Динамика решетки. М.: Мир. 1968. С.156.

14. Лисовский Ф.В., Щеглов В.И. // ЖТФ. 1983. Т.53. №3. С.596.

15. Лисовский Ф.В., Щеглов В.И. // ФТТ. 1983. Т.25. №12. С.3710.

16. Clark A.E., Strakna R.E. // J.Appl.Phys. 1961. V.32. P.1172.

17. Schlömann E., Joseph R.I. // J.Appl.Phys. 1964. V.35. №1. P.167.

18. Schlömann E., Joseph R.I. // J.Appl.Phys. 1964. V.35. №8. P.2382.

19. Schlömann E., Joseph R.I. // J.Appl.Phys. 1965. V.36. №3. Pt.1. P.875.

20. Vashkovsky A.V., Lock E.H., Shcheglov V.I., Zubkov V.I. // IEEE Trans. on Magn. 1990. V.26. №5. P.1480.

21. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // РЭ. 1991. Т.36. №1. С.18.

22. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // ЖТФ. 1990. Т.60. №7. С.138.

23. Зубков В.И., Локк Э.Г., Щеглов В.И. // РЭ. 1990. Т.35. №8. С.1617.

24. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // РЭ. 1993. Т.38. №5. С.818.

25. Анненков А.Ю., Вашковский А.В., Зубков В.И., Щеглов В.И. // РЭ. 1995. Т.40. №7. С.1149.

26. Вашковский А.В., Локк Э.Г., Щеглов В.И. // ЖЭТФ. 1997. Т.111. №3. С.1016.

27. Вашковский А.В., Локк Э.Г., Щеглов В.И. // ЖЭТФ. 1998. Т.114. №4(10). С.1430.

28. Зубков В.И., Щеглов В.И. // РЭ. 2001. Т.46. №4. С.433.

29. Беляева О.Ю., Зарембо Л.К., Карпачев С.Н. // УФН. 1992. Т.162. №2. С.107.

30. Сарнацкий В.М. // ПЖТФ. 1998. Т.24. №8. С.30.

31. Сарнацкий В.М., Мавлоназаров И.О., Луцев Л.В. // ПЖТФ. 2014. Т.40. №14. С.79.

32. Döring W. // Zs. für Naturforsch. 1948. Bd.3a. №7. S.373.

33. Pellam J.R., Galt J.K. // J. Chem. Phys. 1946. V.14. P.608.

34. Бергман Л. Ультразвук. М.: ИЛ. 1956.

35. Ультразвук. Маленькая энциклопедия. Глав.ред. И.П.Голямина. М.: Советская энциклопедия. 1979.

36. Ноздрев В.Ф., Федорищенко Н.В. Молекулярная акустика. М.: Высшая школа. 1974.

37. Ноздрев В.Ф. Применение ультраакустики в молекулярной физике. М.: Физматгиз. 1958.

38. Колесников А.Е. Ультразвуковые измерения. М.: Изд. стандартов. 1970.

39. Френкель Я.И. Электродинамика. М.: ОНТИ. Т.1. 1934. Т.2. 1935.

40. Гуревич А.Г. Магнитный резонанс в ферритах и антиферромагнетиках. М.: Наука. 1973.

41. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Физматлит. 1994.

42. Osborn J.A. // Phys. Rev. 1945. V.67. №11-12. P.351.

43. Вонсовский С.В., Шур Я.С. Ферромагнетизм. М.: ОГИЗ Гостехиздат. 1948.

44. Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред (Теоретическая физика, т.VIII). М.: Наука. 1982.

45. Белов К.П., Звездин А.К., Кадомцева А.М., Левитин Р.З. Ориентационные переходы в редкоземельных магнетиках. М.: Наука. 1979.

46. Тарасенко В.В., Ченский Е.В., Дикштейн И.Е. // ЖЭТФ. 1976. Т.70. №6. С.2178.

47. Малоземов А., Слонзуски Дж. Доменные стенки в материалах с цилиндрическими магнитными доменами. М.: Мир. 1982.

48. Вашковский А.В., Локк Э.Г., Щеглов В.И. // Микроэлектроника. 1998. Т.27. №5. С.393.

49. Вашковский А.В., Локк Э.Г., Щеглов В.И. // ФТТ. 1999. Т.41. №11. С.2034.

50. Ландау Л.Д., Лифшиц Е.М. Теория упругости. (Теоретическая физика, т.VII). М.: Наука. 1965.

51. Sparks M. Ferromagnetic relaxation theory. McGraw-Hill Book Co. 1964.

52. Барьяхтар В.Г., Горобец Ю.И. Цилиндрические магнитные домены и их решетки. Киев: Наукова Думка. 1986.

53. Ганн В.В., Горобец Ю.И. // ФТТ. 1975. Т.17. №5. С.1305.

54. Барьяхтар В.Г., Ганн В.В., Горобец Ю.И. // ФТТ. 1976. Т.18. №7. С.1990.