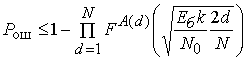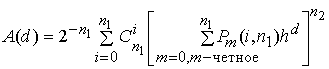УДК 621.391.01
АЛГОРИТМЫ ИТЕРАТИВНОГО ПОСИМВОЛЬНОГО ПРИЕМА БЛОКОВЫХ ТУРБО-КОДОВ НА ОСНОВЕ КОДОВ С ПРОВЕРКОЙ НА ЧЕТНОСТЬ
Л. Е. Назаров, В. В. Батанов, О. О. Кузнецов
Институт радиотехники и электроники им. В.А.Котельникова РАН, Фрязинский филиал
Статья получена 17 сентября 2014 г.
Аннотация. Приведены описания и результаты исследования алгоритмов итеративного приема турбо-кодов, формируемых на основе простейших кодов с проверкой на четность.
Ключевые слова: блоковые турбо-коды, алгоритмы итеративного приема, вероятность ошибки.
Abstract. This paper presents the symbol-by-symbol decoding algorithms for serial block turbo-codes (block product codes) based on simple single-parity-check codes.
Key words: block product codes, iterative decoding, word-rate rate.
Введение
Блоковые турбо-коды входят в класс помехоустойчивых кодов, известных в литературе как коды-произведения [1]. Их особенностью является возможность применения при приеме алгоритмов итеративной обработки входных реализаций, обеспечивающих достижение вероятностно-энергетических характеристик, близких к предельным характеристикам, определяемым пропускной способностью каналов передачи [2].
Особенностью рассматриваемых в настоящей статье блоковых турбо-кодов является то, что они формируются на основе простейших блоковых кодов с проверкой на четность с одним проверочным символом. Это определяет низкую сложность результирующих алгоритмов итеративного приема данных турбо-кодов, что обусловливает их применение в системах связи широкого назначения и в системах хранения данных. В частности, они применяются в оптических системах связи и в системах магнитной записи [3,4]. Кроме того, эти блоковые турбо-коды составляют основу класса последовательных турбо-кодов с пониженной сложностью алгоритмов приема по отношению к алгоритмам приема с параллельным объединением рекурсивных сверточных кодов [5,6].
Исследованию свойств рассматриваемых турбо-кодов посвящен ряд работ, в которых приведены описания эффективных алгоритмов итеративного посимвольного приема, характеризуемых высокой производительностью и осуществляющих подоптимальную обработку входных реализаций без оценки энергетического параметра канала передачи [5,6,7,8].
В настоящей статье приведена методика оценивания энергетических потерь при применении данных алгоритмов по отношению к процедуре оптимального приема, реализующей правило максимального правдоподобия [1], приведены оценочные значения энергетических потерь по отношению к теоретическим оценкам и по отношению к более сложному алгоритму приема, требующего знания относительно энергетического параметра канала передачи.
1. Постановка задачи
Помехоустойчивые коды с параметрами ![]() задаются порождающими матрицами размером
задаются порождающими матрицами размером ![]() [1]. Здесь
[1]. Здесь
![]() ,
, ![]() -
длительность последовательностей символов кодовых слов и информационных
символов.
-
длительность последовательностей символов кодовых слов и информационных
символов.
Порождающие матрицы
рассматриваемых турбо-кодов эквивалентны двумерной матрице - ее строки и
столбцы являются кодовыми словами блоковых кодов ![]() ,
,
![]() с параметрами
с параметрами ![]() ,
, ![]() . Коды
. Коды ![]() ,
, ![]() являются простейшими кодами с проверкой
на четность с единственным проверочным символом. Длительность кодовых слов этих
кодов-произведений равна
являются простейшими кодами с проверкой
на четность с единственным проверочным символом. Длительность кодовых слов этих
кодов-произведений равна ![]() , информационный объем
равен
, информационный объем
равен ![]() , кодовая скорость равна
, кодовая скорость равна ![]() , минимальное расстояние Хэмминга равно
, минимальное расстояние Хэмминга равно ![]() .
.
Известен ряд алгоритмов итеративного приема рассматриваемых турбо-кодов [6,7,8]. При применении этих алгоритмов приема не требуется оценка энергетического параметра канала, что упрощает их реализацию. Вместе с тем, более сложные алгоритмы приема, использующие оценки энергетического параметра, являются более эффективными по отношению к вероятностно-энергетическим характеристикам. Суть рассматриваемой проблемы - сравнительный анализ алгоритмов итеративного приема рассматриваемых турбо-кодов путем компьютерного моделирования и теоретического анализа.
2. Алгоритмы итеративного приема турбо-кодов на основе составляющих блоковых кодов с проверкой на четность
Пусть ![]() - последовательность информационных
символов, образующих матрицу в составе матрицы кодового слова
- последовательность информационных
символов, образующих матрицу в составе матрицы кодового слова ![]() кода-произведения;
кода-произведения; ![]() - реализация на входе декодера, отсчеты
которой представляют сумму сигнальной и помеховой компонентов
- реализация на входе декодера, отсчеты
которой представляют сумму сигнальной и помеховой компонентов
![]() . (1)
. (1)
Здесь ![]() -
амплитуда сигналов с двоичной фазовой манипуляцией (ФМ2),
-
амплитуда сигналов с двоичной фазовой манипуляцией (ФМ2), ![]() - помеховая компонента аддитивного белого
гауссовского шума с односторонней спектральной плотностью
- помеховая компонента аддитивного белого
гауссовского шума с односторонней спектральной плотностью ![]() .
.
В работах [5,6,7,8] приведены описания ряда эффективных алгоритмов итеративного посимвольного приема рассматриваемых турбо-кодов. Исследование данных алгоритмов показали, что наиболее эффективным является алгоритм MIN_SUM_BP [7,8], разработанный для приема низкоплотностных кодов. При его использовании не требуется оценка энергетического параметра канала. Возможность применения соответствующего аппарата определяется тем фактом, что рассматриваемые коды-произведения входят в класс низкоплотностных кодов [7,8].
Перед выполнением
итерации алгоритма MIN_SUM_BP для посимвольного приема кодового символа ![]() производится инициализация величин
производится инициализация величин ![]() ,
, ![]() и
и ![]() ,
, ![]() . Итерация включает выполнение
следующих шагов обработки последовательностей
. Итерация включает выполнение
следующих шагов обработки последовательностей ![]() ,
, ![]() [8]:
[8]:
1) формируются последовательности “жестких”
решений ![]() ,
, ![]() :
: ![]() , если
, если ![]() , иначе
, иначе
![]() и
и ![]() , если
, если ![]() , иначе
, иначе ![]() ,
вычисляются суммы
,
вычисляются суммы  ,
, 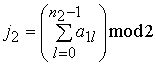 ;
;
2) вычисляются значения ![]() и
и ![]() ;
;
3) вычисляются
нормализованные значения ![]() и
и ![]() по
правилу
по
правилу ![]() ,
, ![]() ;
;
4) для кодового символа ![]() вычисляются новые величины
вычисляются новые величины ![]() ,
, ![]() .
.
5) если критерий
остановки алгоритма итеративного приема не выполняется, то процесс продолжается
с шага 1) итерации. При выполнении критерия остановки итеративной обработки
вычисляются величины ![]() и принимаются решения
относительно значений кодовых символов
и принимаются решения
относительно значений кодовых символов ![]() при
условии
при
условии ![]() , иначе
, иначе ![]() .
.
Более сложным по отношению к изложенному алгоритму MIN_SUM_BP является алгоритм итеративного посимвольного приема BP (belief propagation) [7]. При использовании алгоритма BP требуется оценка энергетического параметра канала, однако, в общем случае этот алгоритм является более эффективным, чем алгоритм MIN_SUM_BP по отношению к вероятностно-энергетическим характеристикам. Приведем описание алгоритма BP.
Перед выполнением
итерации алгоритма BP для посимвольного приема кодового
символа ![]() производится инициализация величин
производится инициализация величин  ,
, ![]() и
и  ,
, ![]() . Итерация включает выполнение
следующих шагов обработки последовательностей
. Итерация включает выполнение
следующих шагов обработки последовательностей ![]() ,
, ![]() :
:
1) вычисляются элементы массивов
![]() и массива
и массива ![]()
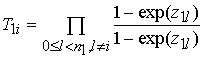 , (2)
, (2)
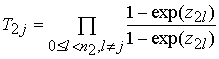 , (3)
, (3)
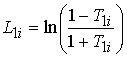 , (4)
, (4)
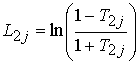 . (5)
. (5)
2) для кодового символа ![]() вычисляются новые величины
вычисляются новые величины ![]() ,
, ![]() .
.
5) если критерий
остановки алгоритма итеративного приема не выполняется, то процесс продолжается
с шага 1) итерации. При выполнении критерия остановки итеративной обработки
вычисляются величины ![]() и принимаются решения
относительно значений кодовых символов
и принимаются решения
относительно значений кодовых символов ![]() при
условии
при
условии ![]() , иначе
, иначе ![]() .
.
3. Методики оценивания вероятностных характеристик посимвольного приема турбо-кодов на основе составляющих кодов с проверкой на четность
Точное вычисление
вероятностных характеристик (вероятность ошибочного приема кодовых слов ![]() , вероятность ошибочного приема
информационных битов
, вероятность ошибочного приема
информационных битов ![]() ) при оптимальном приеме сигналов
представляет сложную проблему [1]. Аналитические выражения относительно
) при оптимальном приеме сигналов
представляет сложную проблему [1]. Аналитические выражения относительно ![]() при наличии канального аддитивного белого
гауссовского шума и при реализации правила максимального приема известны лишь
для ограниченного класса ансамблей сигналов, включающего ансамбли ортогональных
и биортогональных сигналов, ансамбли симплексных сигналов. Более сложной
является задача оценивания вероятностных характеристик для оптимального
посимвольного приема [9,10].
при наличии канального аддитивного белого
гауссовского шума и при реализации правила максимального приема известны лишь
для ограниченного класса ансамблей сигналов, включающего ансамбли ортогональных
и биортогональных сигналов, ансамбли симплексных сигналов. Более сложной
является задача оценивания вероятностных характеристик для оптимального
посимвольного приема [9,10].
Вследствие этого
оценивание вероятностных характеристик исследуемых ансамблей сигналов
производится с использованием формульных соотношений, определяющих верхние
границы вероятностей ![]() и
и ![]() . Для ансамблей
сигналов известны верхние границы
. Для ансамблей
сигналов известны верхние границы ![]() , наиболее используемой
из которых является аддитивная граница [1]. Более точной по отношению к
аддитивной границе является мультипликативная граница при эквивалентной
сложности их вычисления, которая применяется для сигналов с манипуляцией ФМ2 на
основе линейных блоковых двоичных кодов [11]
, наиболее используемой
из которых является аддитивная граница [1]. Более точной по отношению к
аддитивной границе является мультипликативная граница при эквивалентной
сложности их вычисления, которая применяется для сигналов с манипуляцией ФМ2 на
основе линейных блоковых двоичных кодов [11]
Здесь ![]() -
энергия сигналов на бит,
-
энергия сигналов на бит, ![]() - количество кодовых
слов с весом Хэмминга
- количество кодовых
слов с весом Хэмминга ![]() ,
, ![]() -
длительность кодовых слов.
-
длительность кодовых слов.
Известно соотношение,
определяющее связь ![]() и
и ![]() [1]
[1]
Соотношения (6), (7) используются для оценивания вероятностей ошибочных решений для алгоритмов оптимального приема, реализующих правило максимального правдоподобия и правило посимвольного приема соответственно.
При вычислении
соотношения (6) необходимо знание спектра расстояний Хэмминга ![]() . Для рассматриваемых турбо-кодов
относительно
. Для рассматриваемых турбо-кодов
относительно ![]() известно выражение [5]
известно выражение [5]
Количество кодовых слов ![]() с расстоянием Хэмминга
с расстоянием Хэмминга ![]() соответствует множителю при слагаемом
соответствует множителю при слагаемом ![]() в многочлене (8).
в многочлене (8).
Альтернативу изложенной
методике оценивания вероятностных характеристик ансамблей сигналов представляет
компьютерное моделирование соответствующих алгоритмов приема. При его
выполнении производится интервальная оценка вероятности ![]() путем
вычисления частости
путем
вычисления частости ![]() . Здесь
. Здесь ![]() -
число ошибочных решений в последовательности независимых вычислительных
экспериментов объемом
-
число ошибочных решений в последовательности независимых вычислительных
экспериментов объемом ![]() .
.
Требуемое количество
вычислительных экспериментов ![]() определяется размером
доверительного интервала, вероятностью
определяется размером
доверительного интервала, вероятностью ![]() , доверительной вероятностью
, доверительной вероятностью ![]() . При условии
. При условии ![]() справедливо
соотношение [12]
справедливо
соотношение [12]
 , (10)
, (10)
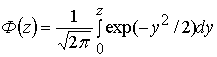 .
.
Например, для ![]() ,
, ![]() (доверительный интервал [
(доверительный интервал [![]() ]),
]), ![]() требуемое
количество экспериментов, вычисленное с использованием (10), оценивается
значением
требуемое
количество экспериментов, вычисленное с использованием (10), оценивается
значением ![]() >1540000.
>1540000.
4. Результаты моделирования
Для ряда рассматриваемых
блоковых турбо-кодов произведено компьютерное моделирование приведенных
алгоритмов итеративного посимвольного приема MIN_SUM_BP и BP с целью оценки
вероятностных характеристик и их сравнительного анализа. При моделировании
выполнялись условия относительно требуемого количества экспериментов ![]() , задаваемого соотношением (10) в
зависимости от оцениваемого значения
, задаваемого соотношением (10) в
зависимости от оцениваемого значения ![]() для параметров
для параметров ![]() ,
, ![]() .
Показано, что применение
20 итераций обеспечивает сходимость вероятностных характеристик.
.
Показано, что применение
20 итераций обеспечивает сходимость вероятностных характеристик.
Результаты моделирования показали, что приведенные алгоритмы итеративного посимвольного приема MIN_SUM_BP и BP рассматриваемых турбо-кодов эквивалентны относительно их вероятностно-энергетических характеристик для АБГШ канала.
В качестве примера на
рис.1 приведены полученные зависимости вероятности ошибки на бит ![]() и вероятности ошибки на кодовое слово
и вероятности ошибки на кодовое слово ![]() от отношения сигнал/помеха
от отношения сигнал/помеха ![]() при применении рассмотренных алгоритмов
итеративного приема для турбо-кода, формируемого на основе блокового кода с
проверкой на четность (10,9): длительность кодовых слов равна
при применении рассмотренных алгоритмов
итеративного приема для турбо-кода, формируемого на основе блокового кода с
проверкой на четность (10,9): длительность кодовых слов равна ![]() , информационный объем равен
, информационный объем равен ![]() при наличии АБГШ. Единая кривая 1 и
кривая 2 относятся к случаю применения алгоритмов итеративного приема MIN_SUM_BP и BP и соответствуют вероятности ошибки
на информационный бит
при наличии АБГШ. Единая кривая 1 и
кривая 2 относятся к случаю применения алгоритмов итеративного приема MIN_SUM_BP и BP и соответствуют вероятности ошибки
на информационный бит ![]() и на кодовое слово
и на кодовое слово ![]() .
.
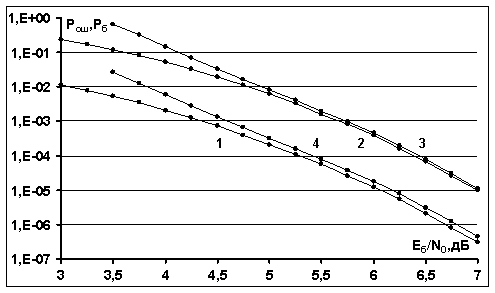
Рис.1. Вероятности ошибки на бит ![]() (кривая 1) и вероятности ошибки на
кодовое слово
(кривая 1) и вероятности ошибки на
кодовое слово ![]() (кривая 2)
(кривая 2)
при применении алгоритмов итеративного приема MIN_SUM_BP и BP для турбо-кода на основе блокового
код
с проверкой на четность (10,9) при наличии АБГШ:
3 - верхняя мультипликативная граница для ![]() ; 4 -
верхняя граница для
; 4 -
верхняя граница для ![]() .
.
Кривая 3 и кривая 4 на
рис.1 соответствуют верхней мультипликативной границе для вероятности ошибки на
кодовое слово ![]() (6) и границе для вероятности ошибки на информационный
бит
(6) и границе для вероятности ошибки на информационный
бит ![]() (7) для рассматриваемого турбо-кода. Вычисление спектра
расстояний Хэмминга
(7) для рассматриваемого турбо-кода. Вычисление спектра
расстояний Хэмминга ![]() произведено с использованием
соотношений (8), (9). Вид спектра приведен на рис.2, количество кодовых
векторов с минимальным расстоянием Хэмминга
произведено с использованием
соотношений (8), (9). Вид спектра приведен на рис.2, количество кодовых
векторов с минимальным расстоянием Хэмминга ![]() равно
2025.
равно
2025.

Рис.2. Спектр расстояний
Хэмминга ![]() турбо-кода, формируемого на основе блокового кода
турбо-кода, формируемого на основе блокового кода
с проверкой на
четность (10,9): длительность кодовых слов ![]() ,
информационный объем
,
информационный объем ![]()
(количество кодовых векторов с минимальным расстоянием
Хэмминга ![]() равно 2025).
равно 2025).
Видно, что вероятностные кривые, полученные путем моделирования, практически совпадают с теоретическими вероятностными кривыми. Это доказывает эффективность алгоритмов итеративного приема MIN_SUM_BP и BP для рассматриваемых турбо-кодов на основе составляющих кодов с проверкой на четность.
На
рис.3 приведены вероятностные характеристики алгоритмов итеративного приема MIN_SUM_BP и BP для турбо-кода на основе блокового
кода с проверкой на четность (10,9) при наличии АБГШ и при релеевских замираниях
сигналов. Кривые получены путем моделирования алгоритмов приема. По оси абсцисс
отложены средние значения сигнал/помеха. Кривая 1 и кривая 2 соответствуют
вероятностям ошибки на бит ![]() для алгоритма BP и для алгоритма MIN_SUM_BP,
полагая известным энергетический параметр канала
для алгоритма BP и для алгоритма MIN_SUM_BP,
полагая известным энергетический параметр канала ![]() . Кривая
3 и кривая 4 соответствуют вероятностям ошибки на кодовое слово
. Кривая
3 и кривая 4 соответствуют вероятностям ошибки на кодовое слово ![]() для алгоритма BP и для алгоритма MIN_SUM_BP. Видно,
что в этом случае энергетический проигрыш при применении алгоритма MIN_SUM_BP по
отношению к алгоритму ВР достигает 0.8 дБ.
для алгоритма BP и для алгоритма MIN_SUM_BP. Видно,
что в этом случае энергетический проигрыш при применении алгоритма MIN_SUM_BP по
отношению к алгоритму ВР достигает 0.8 дБ.
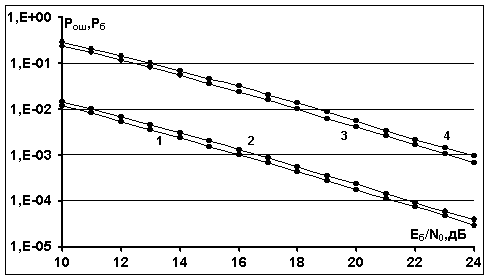
Рис.3. Вероятностные
характеристики алгоритмов итеративного приема для турбо-кода на основе
блокового код
с проверкой на четность (10,9) при наличии АБГШ и при релеевских
замираниях сигналов (по оси абсцисс
отложены средние значения сигнал/помеха):
1
- вероятности ошибки на бит ![]() для алгоритма ВР;
для алгоритма ВР;
2 -
вероятности ![]() для алгоритма MIN_SUM_BP;
для алгоритма MIN_SUM_BP;
3 - вероятности ошибки на кодовое
слово ![]() для алгоритма BP;
для алгоритма BP;
4 - вероятности ошибки ![]() для
алгоритма MIN_SUM_BP.
для
алгоритма MIN_SUM_BP.
Заключение
Приведены описания алгоритмов MIN_SUM_BP и BP (belief propagation) итеративного приема турбо-кодов, формируемых на основе простейших блоковых кодов с одним проверочным символом.
Приведены методики оценивания вероятностных характеристик рассматриваемых турбо-кодов при использовании алгоритмов их итеративного приема.
Путем моделирования для ряда турбо-кодов показано, что алгоритм итеративного приема MIN_SUM_BP без оценки энергетического параметра канала и алгоритм итеративного приема BP, требующего оценок энергетического параметра канала передачи, эквивалентны относительно их вероятностных характеристик при наличии АБГШ. Вероятностные характеристики этих алгоритмов итеративного приема практически совпадают с теоретическими вероятностными характеристиками оптимального приема, реализующего критерий максимального правдоподобия.
Для канала с релеевскими замираниями сигналов и АБГШ энергетический проигрыш при применении алгоритма MIN_SUM_BP по отношению к алгоритму ВР, требующему знания относительно энергетического параметра канала передачи, достигает 0.8 дБ.
Литература
1. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. М.: Мир. 1976. 594 с.
2. Hagenauer J., Offer E., Papke L. Iterative decoding of binary block and convolutional codes. // IEEE Transactions on Information Theory. 1996. V.IT-42. N2. P.429-448.
3. Farhadi G., Jamali S.H. Performance Analysis of Fiber-Optic BPPM CDMA Systems With Single Parity-Check Product Codes. // IEEE Transactions on Communications. 2006. V.54. N9. P.1643-1653.
4. Li J., Narayanan R., Kurtas E., Georghiades C.N. On the Performance of High-Rate TPC/SPC Codes and LDPC Codes Over Partial Response Channels. // IEEE Transactions on Communications. 2002. V.50. N5. P.723-734.
5. Jing Li., Narayanan R., Georghiades .N. Product accumulate codes: a class of codes with near-capacity performance and low decoding complexity. // IEEE Transactions on Information Theory. 2004. V.50. N1. P.31-46.
6. Назаров Л.Е., Головкин И.В. Последовательные высокоскоростные турбо-коды с пониженной сложностью алгоритмов приема. // Радиотехника и электроника. 2010. Т.55. №10. Стр.1193-1199.
7. Ping Li, Chan S., Yeng K.L. Efficient soft-in-soft-out sub-optimal decoding rule for single parity check codes. // Electronic Letters. 1997. V.33. N19. P.1614-1616.
8. Назаров Л.Е., Головкин И.В. Алгоритмы итеративного декодирования кодов-произведений с проверкой на четность. // Журнал радиоэлектроники [электронный журнал]. 2011. №1. URL: http://jre.cplire.ru/jan11/3/text.pdf
9. Назаров Л.Е. Вероятностные характеристики при оптимальном посимвольном приеме сигналов, соответствующих двоичным блоковым кодам. // Радиотехника и электроника. 1999. Т.44. №10. Стр. 1231-1235.
10. Назаров Л.Е., Головкин И.В. Границы ошибки при посимвольном приеме сигналов на основе линейных блоковых кодов. // Известия Вузов. Электроника. 2009. №5. Стр.44-49.
11. Смольянинов В.М., Назаров Л.Е. Мультипликативная граница вероятности правильного распознавания при когерентном приеме. // Радиотехника и электроника. 1987. Т.32. №2. Стр. 446-449.
12. Дунин-Барковский И.В., Смирнов Н.В. Теория вероятностей и математическая статистика в технике. М.: Гос. издательство технико-теоретической литературы. 1955. 556 с.