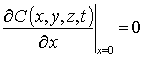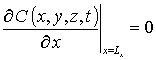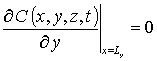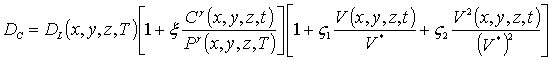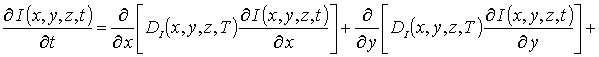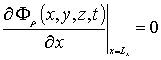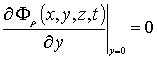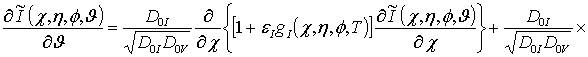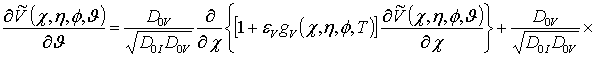Об аналитической методике анализа процессов массо- и теплопереноса
Е. Л. Панкратов 1, Е. А. Булаева 1,2
1 Нижегородский государственный университет им. Н.И. Лобачевского
2 Нижегородский архитектурно-строительный университет
Статья получена 15 сентября 2015 г.
Аннотация. В данной работе рассматривается аналитическая методика анализа и анализ модели формирования полевого гетеротранзистора. Данная методика позволяет проводить анализ нелинейных массо- и теплопереноса в многослойных структурах с переменными во времени параметрами без сшивки решений на границах раздела между слоями многослойных структур. Данный метод проиллюстрирован на примере анализа формирования полевого гетеротранзистора.
Ключевые слова: массо- и теплоперенос; аналитическая методика анализа; оптимизация радиоэлектронных устройств.
Abstract. In this paper we consider an analytical approach for analysis and optimization of formation of a field-effect heterotransistors. The approach gives a possibility to analyse nonlinear mass and heat transport in a multilayer structure with time-varying parameters without crosslinking of solutions on interfaces between layers of the multilayer structure. The approach has been illustrated by analysis of manufacturing of a field-effect heterotransistor.
Keywords: mass and heat transport; analytical approach for analysis; optimization of radio-electronic devices.
Введение
Развитие твердотельной электроники приводит к необходимости уменьшения размеров элементов интегральных схем. К настоящему времени разработаны несколько методов уменьшения размеров данных элементов. Одним из этих методов является выращивание тонкопленочных устройств [1-4]. Вторым методом является диффузионное или ионное легирование необходимых участков образцов или гетероструктур с дальнейшим лазерным или микроволновым отжигом примеси и/или радиационных дефектов [5-7]. Использование данных методов отжига приводит к формированию неоднородного температурного поля и, как следствия, к формированию неоднородности легируемой структуры и уменьшению размеров элементов интегральных схем. Еще одним способом изменения свойств легируемого материала является его радиационная обработка [8,9].
В данной работе рассматривается способ формирования полевого гетеротранзистора с неоднородно легированным каналом. Неоднородное легирование канала при изготовлении полевых транзисторов позволяет изменить скорость переноса носителей заряда [10] и, уменьшив длину канала, предотвратить эффект смыкания истока со стоком [11]. Для иллюстрации предлагаемого метода оптимизации легирования канала рассмотрим гетероструктуру, представленную на рис. 1.
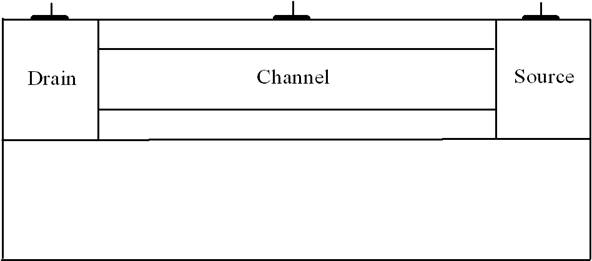
Рис. 1. Рассматриваемая структура полевого гетеротранзистора
Будем считать, что после формирования канала один из его концов легируется с помощью диффузии или ионной имплантации с целью формирования неоднородного профиля легирования. Далее рассматривается микроволновый отжиг примеси и/или радиационных дефектов. Данный тип отжига позволяет прогревать только приповерхностную область для ограничения диффузии вглубь гетероструктуры. После завершения отжига проводится заращивание канала и формирование затвора. Основной целью данной работы является оптимизация длительности отжига с целью легирования необходимой части канала.
Методика анализа
Для достижения поставленных целей определим пространственно- временные распределения концентраций примесей. Искомые распределения найдем путем решения второго закона Фика [10,12-14]
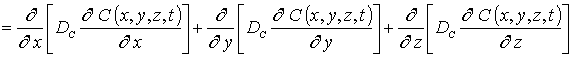 (1)
(1)
с граничными и начальным условиями
 ,
, 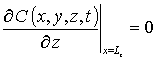 , C (x,y,z,0)=f (x,y,z).
(2)
, C (x,y,z,0)=f (x,y,z).
(2)
В соотношениях (1) и (2) введены следующие обозначения: C(x,y,z,t) - пространственно- временное распределение концентрации примеси, T – температура отжига, DС - коэффициент диффузии примеси. Величина коэффициента диффузии определяется свойствами материалов в слоях гетероструктуры, скорости прогрева и охлаждения гетероструктуры (в соответствии с законом Аррениуса). Зависимости коэффициента диффузии от параметров могут быть аппроксимированы следующим соотношением [9,15,16]
где DL (x,y,z,T) – пространственная (за счет многослойности гетероструктуры) и температурная (по закону Аррениуса) зависимости коэффициента диффузии; P (x,y,z,T) - предел растворимости примеси; определяемый свойствами материала параметр g может принимать целые значения в интервале g Î[1,3] [15]; V (x,y, z,t) - пространственно-временное распределение концентрации радиационных вакансий; V* - равновесное распределение вакансий. Концентрационная зависимость коэффициента диффузии подробно обсуждается в [15]. Следует заметить, что в случае диффузионного легирования радиационные повреждения отсутствуют и z1= z2= 0. Пространственно-временные распределения концентраций радиационных дефектов определялись путем решения следующей системы уравнений [9,16]
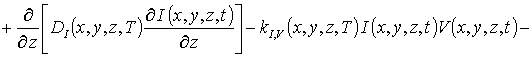
![]() (4)
(4)
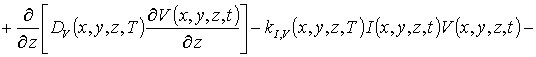
![]()
с начальными
r (x,y,z,0)=fr (x,y,z) (5a)
и граничными условиями
 ,
, 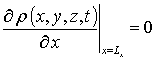 ,
,  ,
, 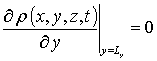 ,
,
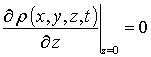 ,
,  . (5б)
. (5б)
В системе уравнений (4) и условиях (5) используются следующие обозначения: r =I,V; I (x,y,z,t) - пространственно-временное распределение концентрации междоузельных атомов; Dr(x,y,z,T) – коэффициенты диффузии междоузельных атомов и вакансий; слагаемые V2(x,y,z,t) и I2(x,y,z,t) соответствуют образованию дивакансий и аналогичных комплексов междоузельных атомов; kI,V(x,y,z,T), kI,I(x,y,z,T) и kV,V(x,y,z,T) - соответственно, параметры рекомбинации точечных дефектов и образования комплексов.
Пространственно-временные распределения концентраций дивакансий FV (x, y,z,t) и аналогичных комплексов междоузельных атомов FI (x,y,z,t) определим с помощью следующей системы уравнений [9,16]
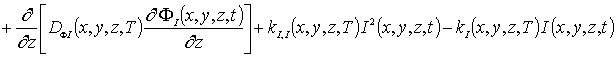 (6)
(6)

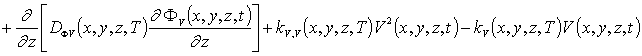
с граничными и начальными условиями
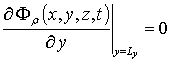 ,
,  ,
,  ,
,
FI (x,y,z,0)=fFI (x,y,z), FV (x,y,z,0)=fFV (x,y,z). (7)
В последних соотношениях введены следующие обозначения: DFI(x,y,z,T) и DFV(x,y,z,T) - коэффициенты диффузии комплексов точечных радиационных дефектов; kI(x,y,z,T) и kV (x,y,z,T) - параметры распада комплексов точечных дефектов.
Для определения пространственно-временных распределений точечных
радиационных дефектов, следуя работам [17-19], представим коэффициенты
диффузии точечных дефектов в следующем виде: Dr(x,y,z,T)=D0r[1+ergr(x,y,z,T)], где D0r - средние значения коэффициентов диффузии, 0≤er< 1, |gr(x,y,z,T)|≤1, r =I,V. В аналогичной форме представим и параметры рекомбинации точечных дефектов и генерации их комплексов: kI,V(x,y,z,T)=k0I,V[1+eI,V gI,V(x,y,z,T)], kI,I(x,y,z,
T)=k0I,I[1+eI,I gI,I(x,y,z,T)] и kV,V(x,y,z,T) = k0V,V [1+eV,V gV,V(x,y,z,T)], где k0r1,r2 – соответствующие средние значения, 0≤eI,V< 1, 0≤eI,I< 1, 0≤eV,V< 1, | gI,V(x,y,z,T)|≤1, |gI,I(x,y,z,T)|≤1, |gV,V(x, y,z,T)|≤1. Введем следующие безразмерные
величины: ![]() , c = x/Lx, h = y/Ly, f = z/Lz,
, c = x/Lx, h = y/Ly, f = z/Lz, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Такая замена изменяет форму записи уравнений (4) и условий (5)
. Такая замена изменяет форму записи уравнений (4) и условий (5)
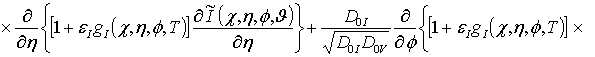

![]() (8)
(8)
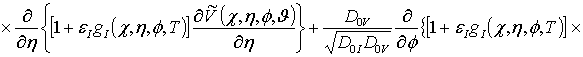
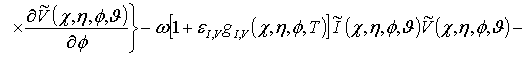
![]()
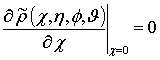 ,
, 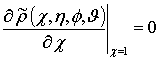 ,
,  ,
,
 ,
,  ,
,  ,
,
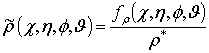 . (9)
. (9)
Решение уравнений (8) с условиями (9) будем искать, следуя [17-19], в виде степенных рядов
![]() . (10)
. (10)
Подстановка
ряда (10) в уравнения (8) и условия (9) позволяет получить уравнения для исходных
приближений концентраций точечных дефектов ![]() и
и ![]() и поправочных функций к ним
и поправочных функций к ним ![]() и
и ![]() , i ³1, j ³1, k ³1. Данные уравнения и условия к ним
приведены в Приложении. Их решения получены стандартным методом Фурье (см.,
например, [20,21]). Полученные решения приведены в Приложении.
, i ³1, j ³1, k ³1. Данные уравнения и условия к ним
приведены в Приложении. Их решения получены стандартным методом Фурье (см.,
например, [20,21]). Полученные решения приведены в Приложении.
Далее определим пространственно-временные распределения концентраций комплексов точечных радиационных дефектов. Для этого представим соответствующие коэффициенты диффузии в следующей форме: DFr(x,y,z,T)=D0Fr[1+ eFrgFr(x,y,z,T)], где D0Fr - средние значения коэффициентов диффузии. Тогда уравнения (6) преобразуются к следующей форме
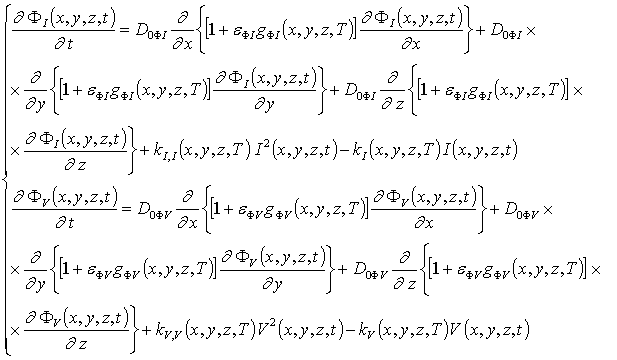
Будем искать решение данных уравнений в виде степенного ряда
![]() . (11)
. (11)
Подстановка ряда (11) в уравнения (6) и соответствующие им граничные и начальные условия позволяет получить уравнения для исходных приближений распределений концентраций комплексов радиационных дефектов Fr0(x,y,z,t) и поправочных функций к ним Fri(x,y,z,t), i ³1, а также граничных и начальных условий к ним. Данные уравнения и условия приведены в Приложении. Решение данных уравнений получено стандартным методом Фурье [20,21] и приведено в Приложении.
Пространственно-временное распределение концентрации примеси определим аналогично пространственно-временному распределению концентрации радиационных дефектов. В рамках данной методики представим аппроксимацию коэффициента диффузии примеси в виде суммы постоянной и переменной составляющих, т.е. DL(x,y,z,T)=D0L[1+eLgL(x,y,z,T)], где D0L - среднее значение коэффициента диффузии примеси, 0£eL< 1, |gL(x,y,z,T)|£1. Далее будем искать решение уравнения (1) в виде степенного ряда
![]() .
.
Подстановка данного ряда в уравнение (1) и условия (2) позволяет получить уравнения для исходного приближения концентрации примеси C00(x,y,z,t), поправочных функций к ним Cij(x, y,z,t) (i ³1, j ³1), граничные и начальные условия к ним. Данные уравнения и условия к ним приведены в Приложении. Их решения получены стандартным методом Фурье (см., например, [20,21]). Решения данных уравнений приведены в Приложении.
Анализ пространственно-временных распределений концентраций примеси и радиационных дефектов проводился аналитически во втором приближении по параметрам, используемым в соответствующем ряде. Данного приближения обычно достаточно для проведения качественного анализа и получения некоторых количественных результатов. Результаты аналитических расчетов проверялись путем их сопоставления с результатами численного моделирования.
Результаты анализа
В данном разделе с помощью ранее полученных соотношений проведен анализ динамики перераспределения примеси с учетом перераспределения радиационных дефектов. Данные соотношения позволили получить пространственные распределения концентрации примеси. Типичные распределения концентрации примеси в направлении, перпендикулярном направлению канала, приведены на рис. 2. Кривая 1 данного рисунка является типичным распределением концентрации примеси вдоль канала. Из данного рисунка следует, что наличие границы раздела между слоями гетероструктуры позволяет получить более компактное и более равномерное распределение концентрации примеси в направлении, перпендикулярном данной границе. Однако в данном случае необходим выбор длительности отжига, т.к. при малых длительностях отжига примесь не достигает границы раздела между слоями гетероструктуры, а при больших длительностях отжига примесь слишком глубоко проникает в соседние слои. Определим компромиссную длительность отжига в рамках введенного ранее критерия [17-19]. В рамках данного критерия аппроксимируем реальное распределение концентрации примеси с помощью идеального прямоугольного распределения y (x,y,z). Далее искомую длительность отжига определим из условия минимума среднеквадратической ошибки
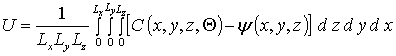 . (12)
. (12)
Зависимости оптимальной длительности отжига приведены на рис. 3. Оптимальная длительность отжига имплантированной примеси принимает меньшие значения, чем оптимальная длительность отжига примеси в случае диффузионного легирования. Причиной такой разницы является необходимость отжига радиационных дефектов.

Рис.2а. Распределения концентрации введенной диффузионно примеси в представленной на рис. 1 гетероструктуре в направлении, перпендикулярном границе раздела между подложкой и эпитаксиальными слоями. Увеличение номера кривой соответствует увеличению разницы между значениями коэффициента диффузии примеси в слоях при условии, что коэффициент диффузии примеси в легированной области больше, чем в соседней

Рис. 2б. Пространственное распределение имплантированной примеси после отжига длительностью Q = 0,0048(Lx2+Ly2+Lz2)/D0 (кривые 1 и 3) и Q = 0,0057(Lx2 +Ly2+Lz2)/D0 (кривые 2 и 4). Кривые 1 и 2 – расчетные распределения в однородной структуре; кривые 3 и 4 - расчетные распределения примеси в двухслойной структуре при условии, что коэффициент диффузии примеси легированном слое больше, чем в соседнем
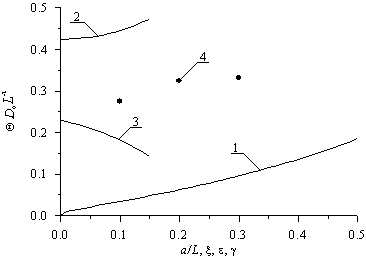
Рис.3а. Зависимости безразмерного оптимального времени отжига введенной диффузионно примеси, полученного из условия минимума среднеквадратической ошибки, от различных параметров гетероструктуры. Кривая 1 – зависимость времени отжига от отношения a/L и x = g = 0 при попарном равенстве коэффициентов диффузии. Кривая 2 - зависимость времени отжига от параметра e при a/L=1/2 и x = g = 0. Кривая 3 - зависимость времени отжига от параметра x при a/L=1/2 и e = g = 0. Кривая 4 - зависимость времени отжига от параметра g при a/L=1/2 и e = x = 0
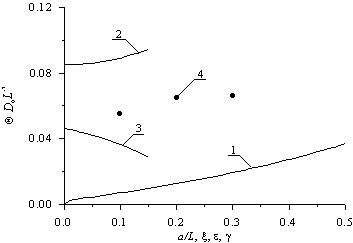
Рис.3б. Зависимости безразмерного оптимального времени отжига введенной с помощью ионной имплантации примеси, полученного из условия минимума среднеквадратической ошибки, от различных параметров гетероструктуры. Кривая 1 – зависимость времени отжига от отношения a/L и x = g = 0 при попарном равенстве коэффициентов диффузии. Кривая 2 - зависимость времени отжига от параметра e при a/L=1/2 и x = g = 0. Кривая 3 - зависимость времени отжига от параметра x при a/L=1/2 и e = g = 0. Кривая 4 - зависимость времени отжига от параметра g при a/L=1/2 и e = x = 0
Заключение
В данной работе рассматривается аналитическая методика анализа и анализ модели формирования полевого гетеротранзистора. Данная методика позволяет проводить анализ нелинейных массо- и теплопереноса в многослойных структурах с переменными во времени параметрами без сшивки решений на границах раздела между слоями многослойных структур. Данный метод проиллюстрирован на примере анализа формирования полевого транзистора с неоднородно легированным каналом. На основе проведенного анализа сформулированы рекомендации по оптимизации технологического процесса с целью формирования более компактного распределения примеси.
Благодарности
Работа поддержана стипендией правительства РФ.
Литература
[1] Г. Волович. Современная электроника. № 2. С. 10-17 (2006).
[2] А. Керенцев, В. Ланин. Силовая электроника. Вып. 1. С. 34-38 (2008).
[3] А.О. Агеев, А.Е. Беляев, Н.С. Болтовец, В.Н. Иванов, Р.В. Конакова, Я.Я. Кудрик, П.М. Литвин, В.В. Миленин, А.В. Саченко. ФТП. Т. 43 (7). С. 897-903 (2009).
[4] Н.И. Волокобинская, И.Н. Комаров, Т.В. Матюхина, В.И. Решетников, А.А. Руш, И.В. Фалина, А.С. Ястребов. ФТП. Т. 35 (8). С. 1013-1017 (2001).
[5] K.K. Ong, K.L. Pey, P.S. Lee, A.T.S. Wee, X.C. Wang, Y.F. Chong, Appl. Phys. Lett. 89 (17), 172111-172114 (2006).
[6] H.T. Wang, L.S. Tan, E. F. Chor. J. Appl. Phys. 98 (9), 094901-094905 (2006).
[7] Ю.В. Быков, А.Г. Еремеев, Н.А. Жарова, И.В. Плотников, К.И. Рыбаков, М.Н. Дроздов, Ю.Н. Дроздов, В.Д. Скупов. Известия вузов. Радиофизика. Т.43 (3). С. 836-843 (2003).
[8] В.В. Козловский, Модификация полупроводников пучками протонов, Наука, Санкт-Петербург, 2003.
[9] В.Л. Винецкий, П.А. Холодарь, Радиационная физика полупроводников, Наукова Думка, Киев, 1979.
[10] И.П. Степаненко. Основы микроэлектроники. Советское радио, М., 1980.
[11] M.V. Dunga, L. Chung-Hsun, X. Xuemei, D.D. Lu, A.M. Niknejad, H. Chenming. Modeling Advanced FET Technology in a Compact Model. IEEE Transactions on Electron Devices. Vol. 53 (9). P. 157-162 (2006).
[12] В.Г. Гусев, Ю.М. Гусев. Электроника, Высшая школа, М., 1991.
[13] Н.А. Аваев, Ю.Е. Наумов, В.Т. Фролкин. Основы микроэлектроники, Радио и связь, М., 1991.
[14] В.И. Лачин, Н.С. Савелов. Электроника, Феникс, Ростов-на-Дону, 2001.
[15] З.Ю. Готра. Технология микроэлектронных устройств, Радио и связь, М.. 1991.
[16] P.M. Fahey, P.B. Griffin, J.D. Plummer. Rev. Mod. Phys. 1989. V. 61. № 2. P. 289-388.
[17] V.L. Vinetskiy, G.A. Kholodar', Radiative physics of semiconductors. ("Naukova Dumka", Kiev, 1979, in Russian).
[18] E.L. Pankratov. Applied Nanoscience. Vol. 2 (1). P. 71-89 (2012).
[19] E.L. Pankratov, E.A. Bulaeva. Reviews in Theoretical Science. Vol. 1 (1). P. 58-82 (2013).
[20] E.L. Pankratov, E.A. Bulaeva. Int. J. Nanoscience. Vol. 11 (5). P. 1250028-1--1250028-8 (2012).
[21] А.Н. Тихонов, А.А. Самарский, Уравнения математической физики, Наука, М., 1972.
[22] H.S. Carslaw, J.C. Jaeger. Conduction of heat in solids (Oxford University Press, 1964).
Приложение
Уравнения
для функций ![]() и
и ![]() , i ³0, j ³0, k ³0 и условия к ним
, i ³0, j ³0, k ³0 и условия к ним
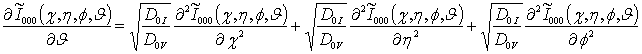
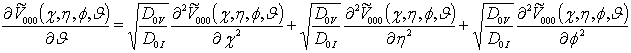 ;
;
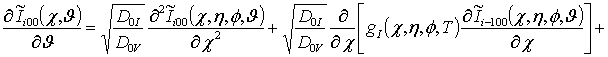
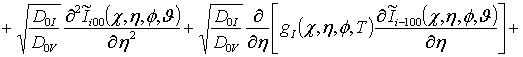


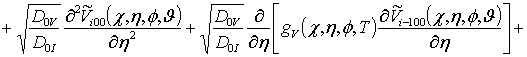
 , i ³1;
, i ³1;

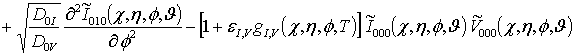
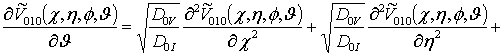
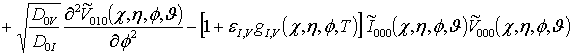 ;
;
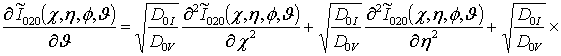
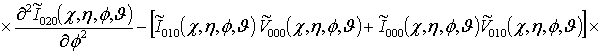
![]()

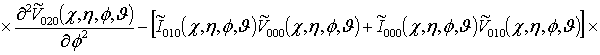
![]() ;
;

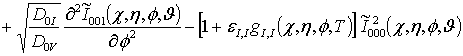

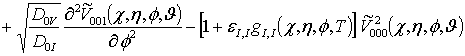 ;
;
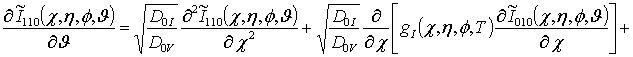


![]()
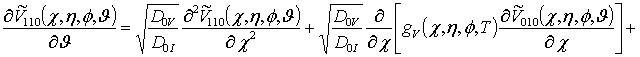
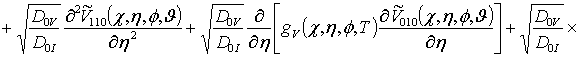
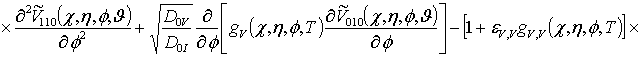
![]() ;
;
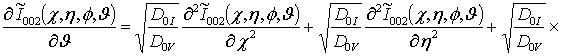
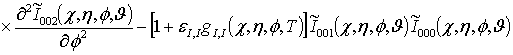

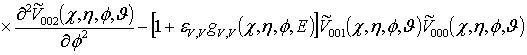 ;
;
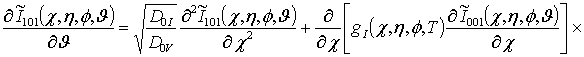
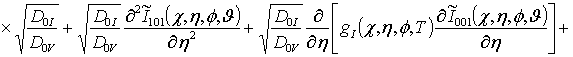
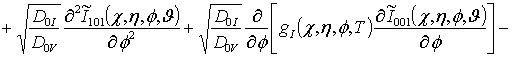
![]()



![]() ;
;

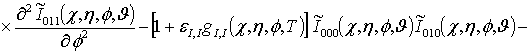
![]()
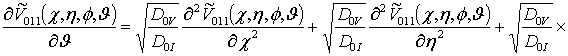

![]() ;
;
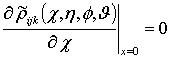 ,
, 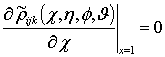 ,
,  ,
,
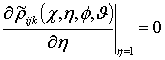 ,
,  ,
,  (i ³0, j ³0, k ³0);
(i ³0, j ³0, k ³0);
![]() ,
, ![]() (i ³1, j ³1, k ³1).
(i ³1, j ³1, k ³1).
Решения данных уравнений с учетом соответствующих граничных и начальных условий представимы в следующей форме
![]() ,
,
где  , cn(c) = cos (p n c),
, cn(c) = cos (p n c), ![]() ,
, ![]() ;
;
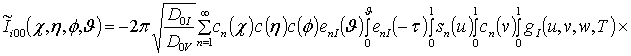

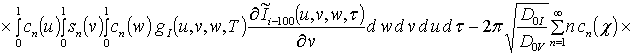
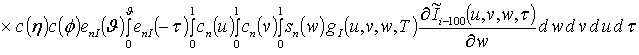
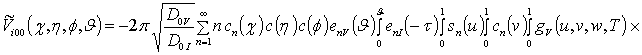
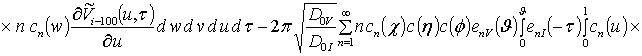

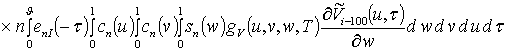 , i ³1,
, i ³1,
где sn(c) = sin (p n c);
![]()
![]() ;
;
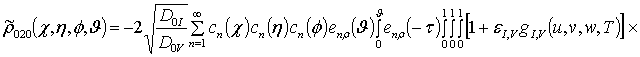
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;

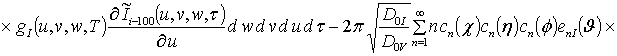

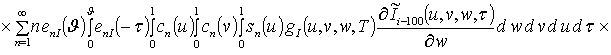
![]()
![]()
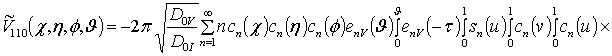
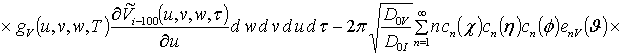
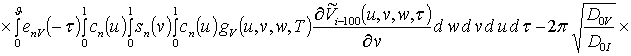
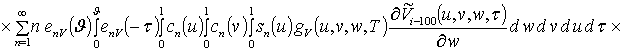
![]()
![]() ;
;

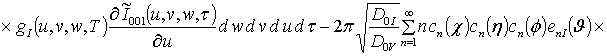


![]()
![]()
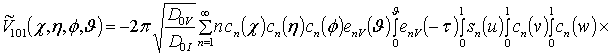
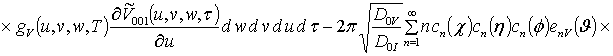


![]()
![]() ;
;
![]()
![]()
![]()
![]()
![]()
![]()
Уравнения для исходных приближений распределений концентраций комплексов радиационных дефектов Fr0(x,y,z,t) и поправочных функций к ним Fri(x,y, z,t), i ³1, а также граничные и начальные условия к ним имеют вид
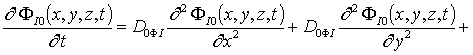
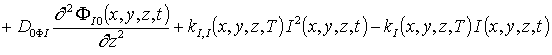
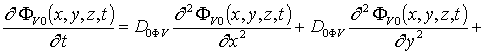
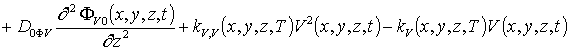 ;
;
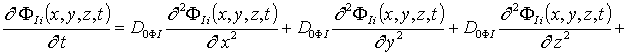
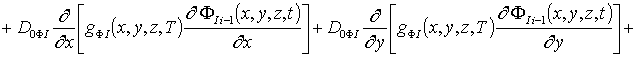
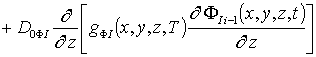
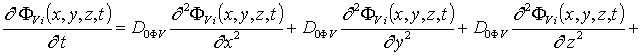
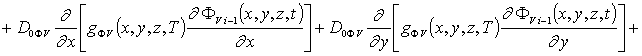
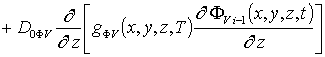 , i³1;
, i³1;
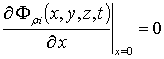 ,
, 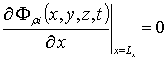 ,
, 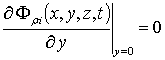 ,
,
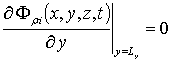 ,
, 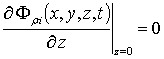 ,
,  , i³0;
, i³0;
Fr0(x,y,z,0)=fFr (x,y,z), Fri(x,y,z,0)=0, i³1.
Решение данных уравнений представимо в следующем виде
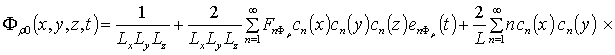
![]()
![]() ,
,
где 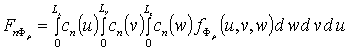 , cn(x) = cos (p n x/Lx),
, cn(x) = cos (p n x/Lx),
![]() ;
;
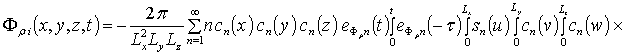

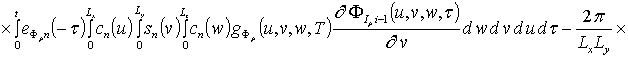
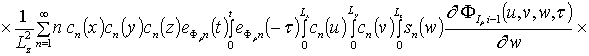
![]() , i³1,
, i³1,
где sn(x) = sin (p n x/Lx).
Уравнения для исходного приближения концентрации примеси C00(x,t), поправочных функций к ним Cij(x,y,z,t) (i ³1, j ³1), граничные и начальные условия к ним имеют следующий вид
 ;
;
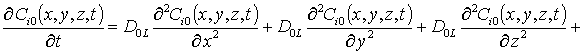
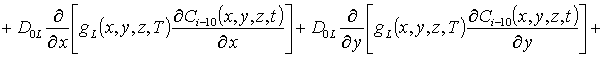
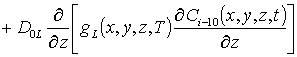 , i ³1;
, i ³1;


 ;
;
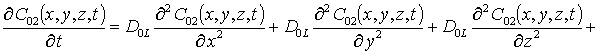
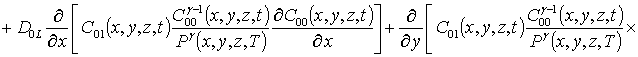
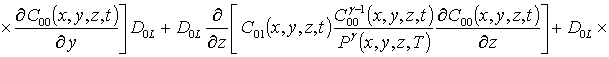

 ;
;
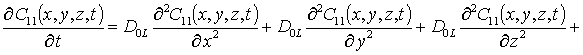
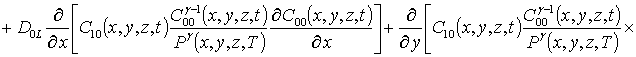
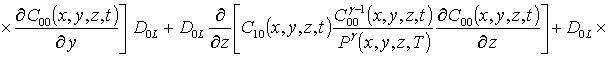

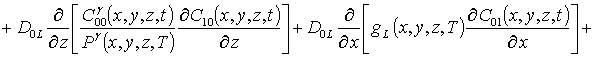
 ;
;
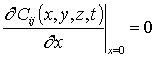 ,
,  ,
, 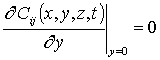 ,
,
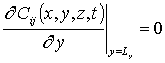 ,
, 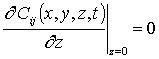 ,
, 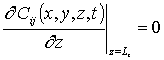 , i ³0, j ³0;
, i ³0, j ³0;
C00(x,y,z,0)=fC (x,y,z), Cij(x,y,z,0)=0, i ³1, j ³1.
Решения данных уравнений с учетом соответствующих граничных и начальных условий представимы в следующей форме
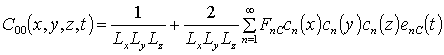 ,
,
где ![]() ,
, ![]()
![]() ;
;
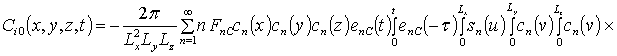
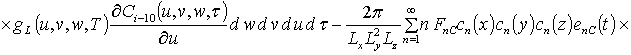


![]() , i ³1;
, i ³1;




![]() ;
;
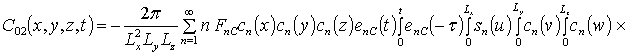
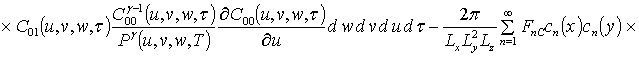
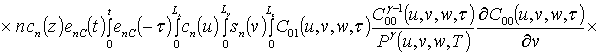


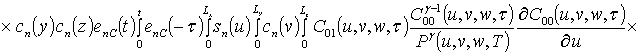
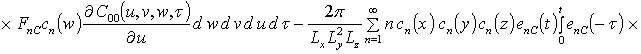
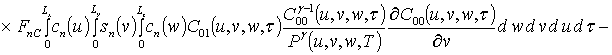


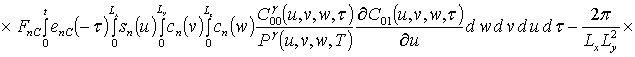
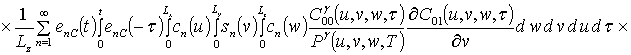

 ;
;



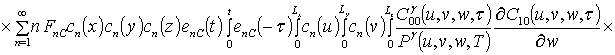

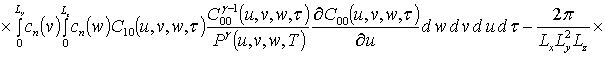

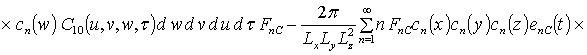
 .
.