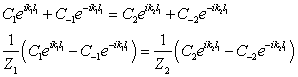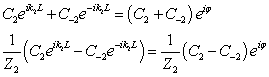Исследование свойств и возможности выделения обратных волн в неоднородных псевдопериодических слоистых средах
И. С. Омельчук, В. А. Солнцев
Московский институт электроники и математики
Национального исследовательского университета
«Высшая школа экономики»
Статья получена 7 сентября 2015 г.
Аннотация. Периодические электродинамические структуры широко применяются для создания мощных электронных приборов, фильтров СВЧ, антенн. Более широкий класс неоднородных сред и замедляющих систем (ЗС) – это псевдопериодические структуры, предложенные для селекции волн, в том числе для подавления или выделения обратных волн. К ним относятся например синхронные спирали (Solntsev Spiral-SS), включающие как частный случай логарифмическую спираль, псевдопериодические волноводы с подавлением паразитных обратных волн. Принцип построения псевдопериодических слоистых сред аналогичен принципу создания псевдопериодических волноводов и основан на согласованном изменении толщины слоев среды вместе с изменением их диэлектрической и магнитной проницаемости, определяющих набег фазы электромагнитного поля на слое. Согласно этому принципу, распределение шага расположения слоев и фазы поля вдоль структуры подбираются так, чтобы сохранить фазовую скорость и амплитуду выбранной пространственной гармоники поля такими же, как в исходной периодической слоистой среде, а амплитуды других пространственных гармоник уменьшить; происходит селекция пространственных гармоник (пространственная селекция). При этом в псевдопериодических слоистых средах можно ожидать выделение обратных пространственных гармоник, то есть получение сред с обратными волнами, имеющими противоположное направление распространения фазы и потока энергии. Исследование свойств распространения электромагнитных волн в псевдопериодических слоистых средах и замедляющих системах открывает возможности создания на этой основе новых микроволновых устройств. Среды с обратными волнами в последние годы привлекают внимание многих исследователей, т.к. имеют новые необычные законы отражения и преломления волн, позволяют получить сверхфокусировку лучей в микроволновом и оптическом диапазонах. В известных работах такие «метасреды» создаются на основе использования периодических электродинамических структур (фотонных или электромагнитных кристаллов). В настоящей работе дан метод и разработана программа расчета свойств электромагнитных волн в псевдопериодической слоистой среде. Рассмотрены некоторые возможности выделения обратных волн в такой среде, определяющие свойства распространения в ней электромагнитных волн.
Ключевые слова: СВЧ, слоистые среды, замедляющие системы, обратные волны, селекция.
Abstract. Periodical electrodynamic structures are widely used to create powerful electronic devices, microwave filters, antennas. A wider class of heterogeneous media and slow-wave systems (SWS) is a pseudoperiodic structure proposed for the selection of waves, including the suppression or amplification of backward waves. These are, for example, synchronous helix (Solntsev Spiral-SS), including as a special case of a logarithmic spiral, with the suppression of pseudoperiodic waveguides parasitic backward waves. The principle of constructing pseudoperiodic-layered media is similar to the principle of creating pseudoperiodic waveguides and based on a consistent change in the thickness of the media’s layers along with the change of electric permittivity and magnetic permittivity, determining the phase shift of the electromagnetic field on the layer. According to this principle, the distribution pitch of the layers and the phase of the field along the structure are selected so as to maintain the phase velocity and amplitude of the selected spatial harmonics of the field the same as in the original periodic layered media and the amplitude of the other spatial harmonics decrease; selection takes spatial harmonics (spatial selection). In the pseudoperiodic-layered media expected to get a selection of backward spatial harmonics, which is the production of media with a backward wave having the opposite direction of propagation phase and energy flow. Investigation of the properties of electromagnetic waves in pseudoperiodic-layered media and slow-wave systems opens the possibility of creating on this basis new microwave devices. Media with a backward wave in recent years attracted the attention of many researchers, because they have new unusual laws of reflection and refraction and allow to obtain focus over beams in the microwave and optical ranges. The well-known works are "metamedia" based on the use of periodic electrodynamic structures (photonic or electromagnetic crystals). This paper presents a method and a program for calculating the properties of electromagnetic waves in a pseudoperiodic-layered media. Also some possibilities of allocation of backward waves in an environment that determine the properties of propagation of electromagnetic waves are shown.
Keywords: microwave, layered media, slow-wave systems, backward waves, selection.
Введение
Периодические электродинамические структуры широко применяются для создания мощных электронных приборов, фильтров СВЧ, антенн. Более широкий класс неоднородных сред и замедляющих систем (ЗС) – это псевдопериодические структуры, предложенные в [1] для селекции волн, в том числе для подавления или выделения обратных волн [2,3]. К ним относятся например синхронные спирали (Solntsev Spiral-SS), включающие как частный случай логарифмическую спираль [1], псевдопериодические волноводы с подавлением паразитных обратных волн [3].
Принцип построения псевдопериодических слоистых сред аналогичен принципу создания псевдопериодических волноводов и основан на согласованном изменении толщины слоев среды вместе с изменением их диэлектрической и магнитной проницаемости, определяющих набег фазы электромагнитного поля на слое. Согласно этому принципу, распределение шага расположения слоев и фазы поля вдоль структуры подбираются так, чтобы сохранить фазовую скорость и амплитуду выбранной пространственной гармоники поля такими же, как в исходной периодической слоистой среде, а амплитуды других пространственных гармоник уменьшить; происходит селекция пространственных гармоник (пространственная селекция). При этом в псевдопериодических слоистых средах можно ожидать выделение обратных пространственных гармоник, то есть получение сред с обратными волнами, имеющими противоположное направление распространения фазы и потока энергии. Исследование свойств распространения электромагнитных волн в псевдопериодических слоистых средах и замедляющих системах открывает возможности создания на этой основе новых микроволновых устройств. Среды с обратными волнами в последние годы привлекают внимание многих исследователей, т.к. имеют новые необычные законы отражения и преломления волн, позволяют получить сверхфокусировку лучей в микроволновом и оптическом диапазонах. В известных работах такие «метасреды» создаются на основе использования периодических электродинамических структур (фотонных или электромагнитных кристаллов [4,5]).
В настоящей работе дан метод и разработана программа расчета свойств электромагнитных волн в псевдопериодической слоистой среде. Рассмотрены некоторые возможности выделения обратных волн в такой среде, определяющие, как и в метаматериалах свойства распространения в ней электромагнитных волн.
В последние годы интенсивно разрабатывается область развития концепций и решения проблем создания метаматериалов («метасред») с отрицательным коэффициентом преломления электромагнитных волн. Эффект отрицательного преломления обусловлен одновременно отрицательными значениями диэлектрической и магнитной проницаемостей (ε <0 и µ <0). Такие материалы часто называют бинегативными средами (DNG, double negative).
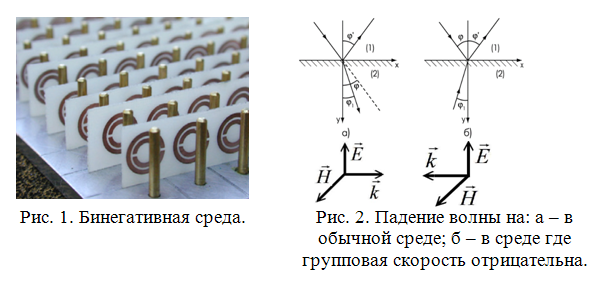
К пониманию физики сред DNG современная наука подходила исподволь и довольно долго. Началось всё с теории обратных волн, одним из ключевых понятий которой явилась отрицательная групповая скорость волны. В практической постановке решение вопроса о существовании волн с отрицательной групповой скоростью принадлежит английскому физику Артуру Шустеру (1851-1934). Он обнаружил формальную возможность отрицательной групповой скорости электромагнитных волн, анализируя формулу из оптики, касающуюся аномальной дисперсии света. А.Шустер впервые показал, что обратные электромагнитные волны возможны при отрицательной групповой скорости, а также что на границе двух сред, в одной из которых распространяется прямая волна, а в другой - обратная, возникает отрицательное преломление (рис.1).
C появлением в 1940-х годах СВЧ-устройств, использующих обратные волны, многие из уже основательно забытых положений теории обратных волн вновь оказались в поле зрения физиков.
Были более детально рассмотрены эффект обратного распространения волн и необычный закон преломления при падении волны из свободного пространства в среду, где групповая и фазовая скорости волн направлены навстречу друг другу. При этом преломленный луч отклоняется в противоположную сторону от нормали к поверхности, нежели при падении на "обычную" среду (рис. 2).
Изучение обратных волн в 1940-е годы прошлого века способствовало не только освоению их практического использования в лампах и антеннах обратной волны, но и всплеску в 1950-е годы теоретического интереса к распространению обратных волн в линиях передачи. В 1957 году Д.В. Сивухин первым отметил, что фазовая и групповая скорости волны будут противоположно направлены в среде с одновременно отрицательными ε и µ (в среде DNG). А уже в 1959 году В.Е.Пафомов теоретически доказал возможность возникновения обратных волн в среде с одновременно отрицательными ε и µ. В том же году Р.А.Силин вновь обратился к иллюстрации закона преломления луча в среде с отрицательной дисперсией, рассматривая кристаллы с обратными волнами.
Наиболее развитую теорию веществ с отрицательным коэффициентом преломления, предложил советский физик В. Г. Веселаго. В 1960-х годах он рассмотрел возможность существования физических сред с отрицательным коэффициентом преломления, обладающих свойствами, парадоксальными с обычной точки зрения. В обычных средах, когда ε > 0 и µ > 0, электромагнитная волна имеет правостороннюю ориентацию тройки векторов H, E, k (магнитная и электрическая компоненты поля, а также волновой вектор). В DNG-среде векторы Умова-Пойтинга и фазовой скорости (волновой вектор k) противоположны, соответственно E, H и k формируют левостороннюю систему координат. Среда с отрицательной рефракцией или с отрицательным индексом преломления (negative refractive index, NRI), а также "леворукие" материалы (left-handed materials, LHM).
Отрицательная величина индекса преломления изменяет геометрическую оптику линз и других объектов, образованных из DNG-материалов. Например, фокусирующая линза становится рассеивающей.
Необходимо отметить работы Р.А.Силина, а именно «О возможности создания плоскопараллельных линз» и «Оптические свойства искусственных диэлектриков», в которых он описал оптические свойства искусственных диэлектриков, а также исследовал особенности плоскопараллельной линзы, выполненной из метаматериала с отрицательным индексом преломления.
Псевдопериодические замедляющие системы и слоистые среды
Распространение волн в периодических замедляющих системах (ЗС) и слоистых средах рассматривалось во множестве работ в связи с применением таких структур в технике и электронике СВЧ. Рассматриваемый здесь более широкий класс неоднородных сред и замедляющие систем – это псевдопериодические структуры, предложенные в [1] для селекции волн, в том числе для подавления или выделения обратных волн [2,3]. В таких системах,меняя вдоль системы её период и одновременно ещё один или несколько параметров , определяющих набег фазы волны на периоде, можно обеспечить постоянство вдоль системы фазовой скорости одной из пространственных гармоник и разрушить другие пространственные гармоники, т.е. существенно уменьшить их амплитуды. При этом изменения периода могут быть значительными, так что система становится неоднородной, «псевдопериодической» в том смысле, что одна из пространственных гармоник сохраняется такой же, как и в исходной периодической системе. В таких псевдопериодических системах возможно увеличение их поперечных размеров без увеличения числа волн.
В периодических ЗС и средах электромагнитное поле имеет ряд свойств, связанных со строгой периодичностью системы вдоль её оси:
· По теореме Флоке имеется дискретный спектр пространственных гармоник поля, соотношение амплитуд которых определяется распределением поля на периоде и величиной периода
· Имеется чередующийся набор полос пропускания и запирания волн по частоте, на ширину и взаимное расположение которых наложен ряд ограничений, обусловленных периодичностью системы.
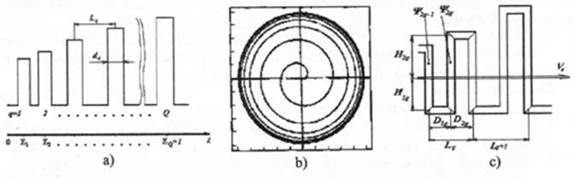
Эти ограничения в значительной мере снимаются в неоднородных псевдопериодических замедляющих системах (ППЗС) с неэквидистантным расположением их элементов (щелей в гребенчатой структуре, диафрагм в круглом волноводе, резонаторов и зазоров взаимодействия электронов и поля в цепочках связанных резонаторов) при определенной связи между шагом расположения элементов и фазой поля в них. В таких волноводах возможно управление спектром пространственных гармоник и мод, в том числе их эффективная селекция при усилении и генерации мощных СВЧ колебаний в электронных приборах со сверхразмерными системами при большом числе мод.
|
|
|
Рис. 3 Псевдопериодические волноводы а) гребенка. b)
синхронная спираль (SS), с) петляющий волновод, |
Вместе с тем, такая неоднородная ППЗС представляет собой фильтр СВЧ, амплитудно-частотная характеристика (АЧХ) и ширина полос прозрачности которого также определяются выбором элементов и шагом их расположения [3].
Известным примером ППЗС может служить плоская логарифмическая спираль. Длина витка в ней прямо пропорциональна изменяющемуся шагу намотки спирали. Поэтому набег фазы на шаге прямо пропорционален величине шага, так что радиальная фазовая скорость основной волны пространственной гармоники постоянна вдоль радиуса, а другие пространственные гармоники подавлены. Основанные на этом свойстве спиральные электродинамические системы используются как логопериодические сверхширокополосные антенны и могут применяться как ЗС для ламп бегущей волны (ЛБВ) с радиальными электронными лучами.
В общем случае указанный принцип селекции можно использовать для создания ППЗС других типов - по существу, каждая периодическая ЗС может быть преобразована в псевдопериодическую, отличающуюся сочетанием указанных выше свойств.
Аналогом псевдопериодических волноводных систем являются неэквидистантные антенные решетки с неравномерным распределением шага и фаз излучателей по решетке, позволяющим устранить побочные главные максимумы излучения. Однако, в отличие от антенн, распределение фаз по элементам ЗС не задано внешними источниками, а определяется формой и размерами элементов системы, которые должны выбираться из условий пространственной и частотной селекции волн. Совместное выполнение условий по селекции пространственных гармоник и формированию необходимой АЧХ фильтра открывает возможность создания новых типов широкополосных одноволновых ЗС.
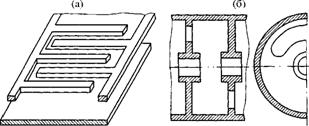
К ЗС петляющего типа можно отнести петляющий волновод, встречные штыри, коаксиально-радиальную линию, цепочку связанных резонаторов при щелях связи, повернутых на 180° (рис. 4), и другие системы, в которых энергия волны переносится в основном вдоль петель системы, многократно пересекая ось ЗС.
|
|
|
Рис. 4. Примеры ЗС петляющего типа: встречные штыри (а), цепочка связанных резонаторов (б). |
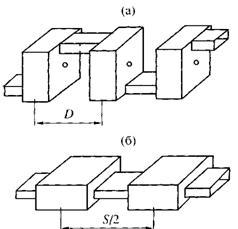
Для расчетов используем волноводно-резонаторную модель (ВРМ) [6], согласно которой ЗС заменяется эквивалентной системой из отрезков волноводов, соответствующих резонаторам с зазорами взаимодействия и щелям связи.
|
|
|
Рис. 5. Волноводно-резонаторная модель петляющей ЗС: эквивалентная система для петляющей ЗС (а), линейная модель эквивалентной системы (б). |
На рис. 5а показана эквивалентная система для петляющей ЗС, а на рис. 5б - ее простейший линейный вариант, учитывающий отражения волны только на стыках волноводов разного поперечного сечения.
Для
моделирования ППЗС будем использовать эквивалентную систему, представленную
на рис. 5б, полагая ее ограниченной по длине, а параметры входящих в нее
отрезков волноводов в общем случае различными. Описание отрезков волноводов и
эквивалентной системы в целом удобно проводить с помощью матриц передачи
четырехполюсников и их каскадного соединения. При этом можно расширить класс
рассматриваемых систем на неоднородные гребенчатые структуры,
диафрагмированные волноводы и подобные им, если брать соответствующие матрицы
передачи четырехполюсников, представляющих отдельные ячейки системы. Для
описания дисперсионных свойств ППЗС вместо диаграммы Бриллюэна используется
введенная ранее амплитудная поверхность дисперсии [3]. Она представляет
распределение пространственной спектральной плотности выбранной компоненты поля
![]() над всей плоскостью волновых чисел в
ЗС
над всей плоскостью волновых чисел в
ЗС ![]() и в свободном пространстве
и в свободном пространстве ![]() . Поверхность определяется путем пространственного преобразования Фурье
электромагнитного поля, найденного по ЗD-кодам или более простым моделям. В периодических системах
эта поверхность вырождается в систему гребней, проекции которых на плоскость
. Поверхность определяется путем пространственного преобразования Фурье
электромагнитного поля, найденного по ЗD-кодам или более простым моделям. В периодических системах
эта поверхность вырождается в систему гребней, проекции которых на плоскость
![]() ,
,
![]() определяют дисперсионные
характеристики пространственных гармоник, т.е. диаграмму Бриллюэна. Для ППЗС
амплитуда одной рабочей пространственной гармоники (и высота соответствующего
ей гребня) сохраняются, амплитуды остальных пространственных гармоник
уменьшаются и получается непрерывный спектр
определяют дисперсионные
характеристики пространственных гармоник, т.е. диаграмму Бриллюэна. Для ППЗС
амплитуда одной рабочей пространственной гармоники (и высота соответствующего
ей гребня) сохраняются, амплитуды остальных пространственных гармоник
уменьшаются и получается непрерывный спектр ![]() .
.
Исследование полосовых частотных свойств и расчет передаточной АЧХ отрезка ППЗС проводится через входной коэффициент отражения или через параметры рассеяния с учетом нагрузок на концах этого отрезка. Из АЧХ находятся полосы пропускания по заданному уровню коэффициента отражения без решения дисперсионного уравнения. Подобный метод применяется и при расчете слоистых сред, однако в псевдопериодических волноводах возможны сложные зависимости параметров отдельных четырехполюсников (слоев) от частоты.
Метод расчета полосовых свойств псевдопериодических структур
Псевдопериодическая
структура является СВЧ-фильтром, АЧХ которого определяется свойствами элементов
и шагами их расположения. Для вычисления частотных характеристик представим
систему цепочкой четырехполюсников, с подключенными входной ![]() и выходной
и выходной ![]() проводимостями нагрузки (рис. 6).
проводимостями нагрузки (рис. 6).
|
|
|
Рис.6 Модель псевдопериодической структуры в виде четырёхполюсников. |
В
общем случае четырехполюсники не идентичны, а их число
Р для ЗС не совпадает с числом зазоров взаимодействия Q в резонаторных ЗС с дискретным взаимодействием электронного
потока и поля в вакуумных приборах СВЧ. Фильтровые
свойства, полосы пропускания и запирания системы описываются частотной
зависимостью входного коэффициента отражения ![]() .
.
Для
вычисления коэффициента отражения можно использовать стандартные процедуры перемножения
матриц передачи ![]() или
известные программы вычисления матриц рассеяния электродинамических систем.
или
известные программы вычисления матриц рассеяния электродинамических систем.
Рассмотрим
более простой способ вычисления ![]() . Введем локальный
. Введем локальный ![]() и полный
и полный ![]() коэффициенты отражения на входе p-го
четырехполюсника:
коэффициенты отражения на входе p-го
четырехполюсника:
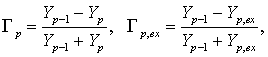 (1)
(1)
где ![]() ,
, ![]() - волновая и входная проводимость p-го
четырехполюсника соответственно. Будем считать четырехполюсники,
соответствующие отдельным элементам ППЗС, горизонтально симметричными.
Коэффициенты их матрицы передачи
- волновая и входная проводимость p-го
четырехполюсника соответственно. Будем считать четырехполюсники,
соответствующие отдельным элементам ППЗС, горизонтально симметричными.
Коэффициенты их матрицы передачи
![]() ,
обладают следующими свойствами:
,
обладают следующими свойствами: ![]() ,
, ![]() , а волновая проводимость
, а волновая проводимость ![]() и набег фазы
и набег фазы ![]() определяются соотношениями:
определяются соотношениями:
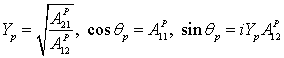 . (2)
. (2)
Входящий
в цепочку p-й четырехполюсник имеет нагрузку
![]() , и,
следовательно, его входная проводимость
, и,
следовательно, его входная проводимость
![]() определяется
рекуррентным выражением
определяется
рекуррентным выражением
 (3)
(3)
Оно
позволяет определить входную проводимость через проводимость нагрузки ![]() в конце цепочки.
Из выражений для
в конце цепочки.
Из выражений для ![]() ,
, ![]() и
и ![]() получаем рекуррентные соотношения для
коэффициента отражения
получаем рекуррентные соотношения для
коэффициента отражения
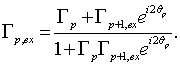 (4)
(4)
Соотношение
для ![]() и приведенное ниже
выражение для спектральной плотности поля
и приведенное ниже
выражение для спектральной плотности поля ![]() являются основой для совместного анализа полос
пропускания и существующих в них пространственных гармоник поля
псевдопериодических ЗС и слоистых сред. Значения входящих в них фаз
являются основой для совместного анализа полос
пропускания и существующих в них пространственных гармоник поля
псевдопериодических ЗС и слоистых сред. Значения входящих в них фаз ![]() и
и ![]() локальных коэффициентов отражения
локальных коэффициентов отражения ![]() определяются структурой
конкретных вариантов ЗС. В частности, в ВРМ в качестве отдельных элементов
берутся отрезки волноводов с длинами
определяются структурой
конкретных вариантов ЗС. В частности, в ВРМ в качестве отдельных элементов
берутся отрезки волноводов с длинами ![]() , фазовыми
постоянными
, фазовыми
постоянными ![]() и
эквивалентными волновыми проводимостями
и
эквивалентными волновыми проводимостями
![]() .
Элементы матрицы передачи для них имеют вид
.
Элементы матрицы передачи для них имеют вид
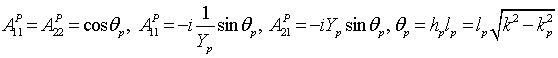 , (5)
, (5)
где ![]() волновое
число в свободном пространстве,
волновое
число в свободном пространстве, ![]() критическое
волновое число рассматриваемой моды
p-го отрезка волновода.
критическое
волновое число рассматриваемой моды
p-го отрезка волновода.
Каждый
элемент описывается двумя параметрами - волновой проводимостью ![]() и электрической
длиной
и электрической
длиной ![]() . Как видно из
приведенных выше соотношений, такое описание справедливо не только для отрезков
волноводов или длинных линий, но и для элементов другого вида, описываемых
симметричными четырехполюсниками. Отличаются только их зависимости
проводимости
. Как видно из
приведенных выше соотношений, такое описание справедливо не только для отрезков
волноводов или длинных линий, но и для элементов другого вида, описываемых
симметричными четырехполюсниками. Отличаются только их зависимости
проводимости ![]() и фазы
и фазы ![]() от частоты. Рекуррентные
соотношения для
от частоты. Рекуррентные
соотношения для ![]() позволяют
рассчитывать коэффициент отражения и АЧХ для разнообразных периодических и
непериодических структур в одномодовом приближении с учетом зависимости
параметров элементов от частоты.
позволяют
рассчитывать коэффициент отражения и АЧХ для разнообразных периодических и
непериодических структур в одномодовом приближении с учетом зависимости
параметров элементов от частоты.
Метод и программа анализа и селекции волн в псевдопериодических слоистых средах
Для выявления возможностей выделения обратных волн надо описать не только внешние частотные свойства, но и провести исследование структуры полей внутри системы.
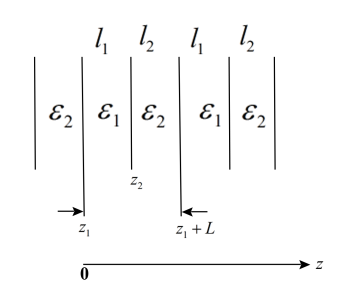
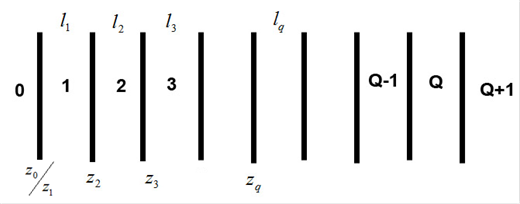
Рассматривается псевдопериодическая слоистая среда (рис.7).
|
|
|
Рис. 7. Псевдопериодическая слоистая среда. |
Система состоит из M слоёв, каждый
из которых может обладать произвольным значением диэлектрической ![]() и магнитной
и магнитной ![]() проницаемостей;
каждый слой имеет свою толщину
проницаемостей;
каждый слой имеет свою толщину![]() . Для упрощения
расчетов все переменные величины записываются в относительных единицах (
. Для упрощения
расчетов все переменные величины записываются в относительных единицах (![]() где
где ![]() и
и ![]() ―относительные электрическая и
магнитная проницаемости соответственно,
―относительные электрическая и
магнитная проницаемости соответственно, ![]() –
некоторое число, а
–
некоторое число, а ![]() полная длина системы).
полная длина системы).
Волна попадает на границу первого
слоя и, зная входной коэффициент отражения![]() последующего
слоя и локальный коэффициент отражения
последующего
слоя и локальный коэффициент отражения ![]() на
данном слое, можно рассчитать значение коэффициента отражения на входе
на
данном слое, можно рассчитать значение коэффициента отражения на входе ![]() :
:
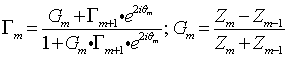 , (6)
, (6)
где 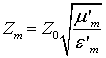 волновое
сопротивление каждого слоя, а
волновое
сопротивление каждого слоя, а 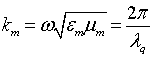 – волновое число,
длина волны в m-м слое
– волновое число,
длина волны в m-м слое 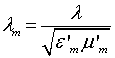 ,
, ![]() длина волны в вакууме,
длина волны в вакууме, 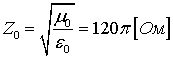 ― волновое сопротивление вакуума.
― волновое сопротивление вакуума.
Плоские волны, которые
распространяются поперёк слоев, имеют две компоненты ![]() и
и
![]() . Учитывая это при решении уравнений
Максвелла, получаем следующие выражения для поля в m-ом слое:
. Учитывая это при решении уравнений
Максвелла, получаем следующие выражения для поля в m-ом слое:
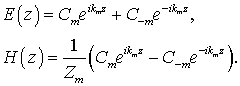 (7)
(7)
Используя условия непрерывности на
границах слоев ![]() , можно найти связь амплитуд
прямых и отраженных волн в m-ом слое и получить следующие рекуррентные
соотношения для амплитуд этих волн
, можно найти связь амплитуд
прямых и отраженных волн в m-ом слое и получить следующие рекуррентные
соотношения для амплитуд этих волн ![]() и
и ![]() соответственно:
соответственно:
|
и |
где ![]() ― толщина j-го
слоя. Далее необходимо записать распределение полей в каждом слое, для
последующего анализа.
― толщина j-го
слоя. Далее необходимо записать распределение полей в каждом слое, для
последующего анализа.
Для получения распределения поля по
волновым числам (![]() ), определенным всеми слоями,
необходимо провести преобразование Фурье по полю и вычислить спектральную
плотность.
), определенным всеми слоями,
необходимо провести преобразование Фурье по полю и вычислить спектральную
плотность.
Переходя к сумме интегралов по длине каждого слоя, получим:
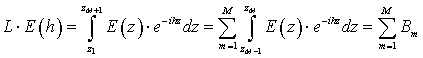 (10)
(10)
Проводя это преобразование и суммирование, учтем,
что 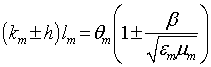 и обозначим
и обозначим ![]() . В
итоге получаем промежуточные выражения для спектральной плотности поля всей
псевдопериодической системы в зависимости от нормированного волнового числа
. В
итоге получаем промежуточные выражения для спектральной плотности поля всей
псевдопериодической системы в зависимости от нормированного волнового числа ![]()
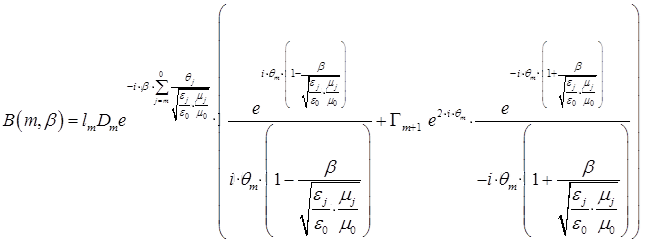
Пусть
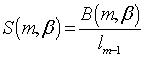 .
.
Производя подстановку, получаем выражение для спектральной плотности поля всей псевдопериодической системы от нормированного волнового числа.
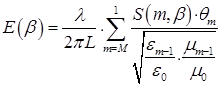
Программа анализа и селекция обратной волны в двухслойных псевдопериодических слоистых средах
Для исследования возможностей выделения обратной волны будем проводить расчеты в два этапа. Сначала рассматриваем двухслойную или четырехслойную периодическую среду и рассчитываем дисперсию и амплитуды пространственных гармоник в ней. Затем переходим к псевдопериодической среде, меняя параметры среды по парам или по четверкам слоёв с целью выделения обратной волны и подавления прямой волны.
Задается периодическая среда с периодом L, состоящим из двух слоев
на периоде. Для каждого слоя задаются значения диэлектрической ![]() , магнитной
, магнитной ![]() проницаемостей
и толщины
проницаемостей
и толщины ![]() . Общая схема представлена на рис. 8.
. Общая схема представлена на рис. 8.
|
|
|
Рис. 8 Двухслойная периодическая система с бесконечным числом периодов. |
Для начала определим частотные
характеристики данной системы. Представим её на одном периоде цепочкой двух
неидентичных четырехполюсников. Для вычисления дисперсии используем стандартные
процедуры перемножения матриц
передачи ![]() . Коэффициенты их матрицы передачи
. Коэффициенты их матрицы передачи
![]() , обладают следующими
свойствами:
, обладают следующими
свойствами: ![]() ,
, ![]() , где
, где
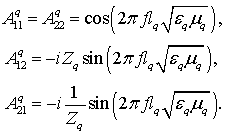 (11)
(11)
Перемножая матрицы ![]() и
и ![]() ,получаем уравнение дисперсии:
,получаем уравнение дисперсии:
где ![]() .
.
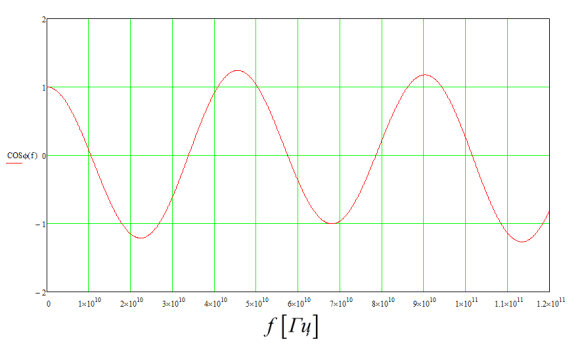
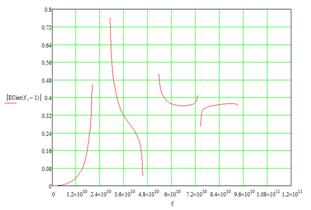
График зависимости дисперсии бесконечно периодической системы от частоты представлен на рис. 9.
|
|
|
Рис. 9. Дисперсия для конкретной
двухслойно-периодической структуры с параметрами: |
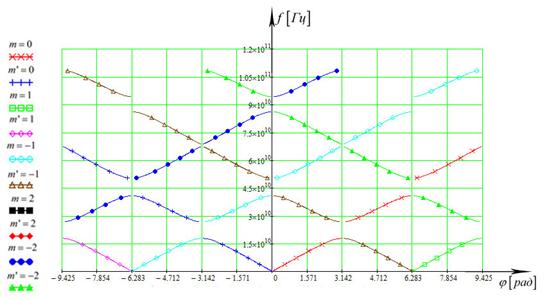
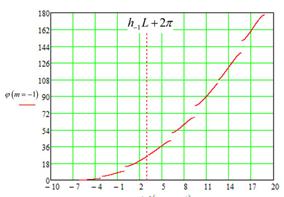
Теперь находим значение ![]() – набег фазы на периоде и строим
дисперсионные характеристики пространственных гармоник. Решая уравнение (12),
получим
– набег фазы на периоде и строим
дисперсионные характеристики пространственных гармоник. Решая уравнение (12),
получим 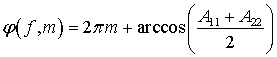 (рис.10), где m – номер пространственной гармоники.
(рис.10), где m – номер пространственной гармоники.
|
|
|
Рис. 10.
Дисперсионные характеристики пространственных гармоник для системы с
параметрами рис.9; |
Из рис. 3 видно, что меняя параметры
системы, можно менять ширину зон пропускания и запирания. Для определения
амплитуд пространственных гармоник учтем, что в данной системе (рис.4)
распространяются плоские волны, и, соответственно, они имеют две компоненты ![]() и
и ![]() .
Учитывая это при решении уравнений Максвелла, получаем:
.
Учитывая это при решении уравнений Максвелла, получаем:
для первого слоя
 (13)
(13)
и аналогично для второго слоя:
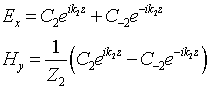 (14)
(14)
где ![]() – волновое
сопротивление каждого слоя,
– волновое
сопротивление каждого слоя, ![]() – волновое число.
– волновое число.
Запишем условие Флоке для одномерно-периодических структур в следующем виде:
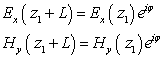 (15)
(15)
Далее воспользуемся
для (8) и (9) условием непрерывности поля при ![]() ,
получаем:
,
получаем:
а, учитывая теорему Флоке, имеем:
так как ![]() .
.
Теперь можно составить из (16) и (17)
систему линейных алгебраических уравнений и решить её, перенеся все члены с ![]() вправо. Далее выражаются все амплитуды
прямых и отраженных волн через амплитуду прямой волны первого слоя, которую мы
заранее задаём.
вправо. Далее выражаются все амплитуды
прямых и отраженных волн через амплитуду прямой волны первого слоя, которую мы
заранее задаём.
Для получения амплитуд
пространственных гармоник ![]() , необходимо провести
преобразование Фурье по полю.
, необходимо провести
преобразование Фурье по полю.
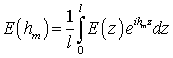 (18)
(18)
Разбивая интеграл на два, суммируем интегралы по длине каждого слоя. Для данного случая в итоге получаем
 (19)
(19)
где ![]() , а m – номер пространственной гармоники.
, а m – номер пространственной гармоники.
Выражая с помощью уравнений (16), (17) амплитуды прямых и отраженных волн через амплитуду прямой волны первого слоя, можно вычислить интегралы (19) и найти амплитуды для разных пространственных гармоник. Соответствующие графики приведены на рис.11.
|
а)
|
б)
|
в)
|
|
Рис. 11 Зависимость амплитуд пространственных гармоник от частоты в полосах пропускания для системы слоёв с параметрами: а) |
||
Дальнейшая задача заключается в выборе
частоты, которая попадает в полосу пропускания для минус первой гармоники (![]() , рис. 11) и для которой амплитуда
этой принимает большое значение (рис. 11в)
, рис. 11) и для которой амплитуда
этой принимает большое значение (рис. 11в) ![]() ).
).
Выбираем приемлемые значения
диэлектрической проницаемости ![]() и частоты
и частоты![]() .
.
Теперь задается псевдопериодическая слоистая среда (рис. 12).
|
|
|
Рис.12 Псевдопериодическая слоистая среда. |
Среда состоит из ![]() слоёв, которое задаются в самом начале
расчета. Соотношения диэлектрических проницаемостей
слоёв, которое задаются в самом начале
расчета. Соотношения диэлектрических проницаемостей ![]() и
толщин слоев
и
толщин слоев ![]() для исходной периодической
системы оставляем без изменений.
для исходной периодической
системы оставляем без изменений.
Следующий шаг заключается в выборе
параметров слоёв для псевдопериодической системы. Для этого на заданной частоте
![]() выбираем волновое число для
выбираем волновое число для ![]() -ой гармоники (рис. 12)
-ой гармоники (рис. 12)
![]() (20)
(20)
где ![]() – период бесконечно
периодической системы (рис.8).
– период бесконечно
периодической системы (рис.8).
Для выделения обратной волны необходимо, чтобы сохранялось условия синхронизма на каждом шаге:
![]() (21)
(21)
где ![]() меняются для каждой
пары слоёв, но соотношение между этими величинами остаётся постоянным
меняются для каждой
пары слоёв, но соотношение между этими величинами остаётся постоянным ![]() . Существует возможность подбора
параметров слоев за счет изменения толщины слоя или изменения диэлектрической
проницаемости слоя (рис. 13). Необходимо заметить, что эти зависимости могут
быль как линейными, так и иметь другой характер.
. Существует возможность подбора
параметров слоев за счет изменения толщины слоя или изменения диэлектрической
проницаемости слоя (рис. 13). Необходимо заметить, что эти зависимости могут
быль как линейными, так и иметь другой характер.
|
|
|
|
а) б) Рис.13. а) подбор параметров слоев за счет изменения диэлектрической проницаемости слоя; б) подбор параметров слоев за счет изменения толщины слоя |
|
По аналогии с предыдущей программой, необходимо найти амплитуды прямых и отраженных волн. Учитывая плоские волны, распространяющиеся поперёк q-го слоя, получаем выражение для поля в этом слое:
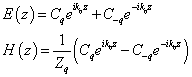 (22)
(22)
Для упрощения расчетов необходимо произвести нормировку амплитуд, для этого обозначим амплитуды следующим образом:
![]() (23)
(23)
В данной системе так же справедливо условие непрерывности:
![]() (24)
(24)
Таким образом, подставляя в (22) выражение (23) с учетом (24), получаем систему уравнений для нормированных амплитуд:
 (25)
(25)
где ![]() – прямая и встречная
нормированные амплитуды q+1-го
слоя.
– прямая и встречная
нормированные амплитуды q+1-го
слоя.
Существует два варианта, зависящих от расстановки
границ слоев, но в обоих случаях возникает мнимая граница, следовательно, для
удобства расчета совместим координаты ![]() и
и ![]() (рис.12). Применяя условие (24) для слоёв
«0» и «1» получаем следующие выражения:
(рис.12). Применяя условие (24) для слоёв
«0» и «1» получаем следующие выражения:
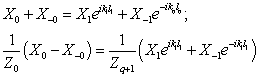 (26)
(26)
Далее составляем систему линейных алгебраических уравнений и решаем её.
Для получения распределения поля по
волновым числам (![]() ), определенным всеми слоями,
необходимо провести преобразование Фурье по полю и вычислить спектральную
плотность.
), определенным всеми слоями,
необходимо провести преобразование Фурье по полю и вычислить спектральную
плотность.
 (27)
(27)
где ![]() – полная длина всей
системы.
– полная длина всей
системы.
Суммируем интегралы по длине каждого слоя.
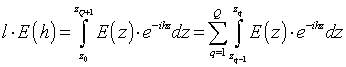 (28)
(28)
Проводя это преобразование и подставляя результаты решения СЛАУ (25, 26) получаем выражение для спектральной плотности поля всей псевдопериодической системы от нормированных амплитуд:
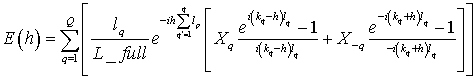 (28)
(28)
Выделение обратной волны в псевдопериодической среде
Выбираем параметры периодической системы, которые будут взяты за основу в наших расчетах.
Для этого рассмотрим три случая.
Возьмем бесконечно периодическую
двухслойную систему, для которой относительная диэлектрическая проницаемость
равна ![]() для первого и второго слоя соответственно.
для первого и второго слоя соответственно.
Рассчитаем спектральную плотность
данной системы для ![]() гармоники.
гармоники.
Рассмотрим три случая для ![]() :
:
А) ![]() ,
,
Б) ![]() ,
,
В) ![]() .
.
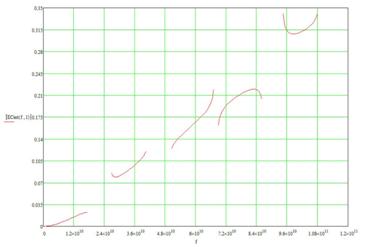
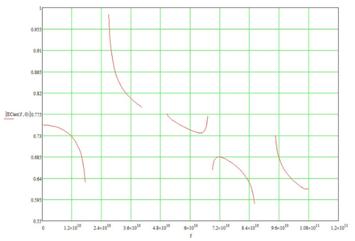
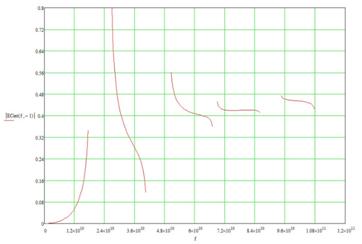
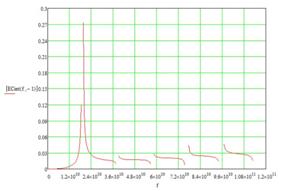
Графики спектральных плотностей для каждого случая представлены на рис.14
|
а) |
б) |
|
в) Рис.14 Спектральная плотность
бесконечно периодической системы а) б) в)
|
|
Как видно по рис. 14,
максимальное значение спектральная плотность достигает при ![]() во второй полосе пропускания. Значит, для
дальнейших расчетов предпочтительнее взять параметры системы рис.14 б).
во второй полосе пропускания. Значит, для
дальнейших расчетов предпочтительнее взять параметры системы рис.14 б).
Далее выбираем рабочую
частоту. Для расчета возьмем ![]() .
.
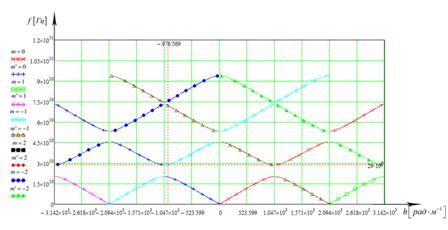
Построим
пространственные гармоники и вычисляем значения ![]() для
выбранной частоты (рис. 15).
для
выбранной частоты (рис. 15).
|
|
|
Рис.15 Выбор волнового числа для выделения обратной волны. |
Вычислив значения
волнового числа для ![]() -ой гармоники
-ой гармоники ![]() вычисляем параметры других слоёв ,
сохраняя при этом условие синхронизма
вычисляем параметры других слоёв ,
сохраняя при этом условие синхронизма![]() , которое для
, которое для ![]() -ой гармоники примет вид:
-ой гармоники примет вид:
![]() .
.
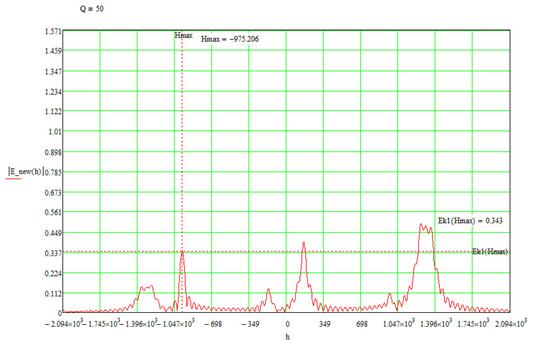
Далее представлены спектральные плотности рассматриваемой системы для Q=50(рис. 16) и Q=100 (рис. 17), где Q – количество слоев в системе. Нетрудно заметить, что с увеличением слоев, величина спектральной плотности начинает изменяться. Однако для обратной волны этот процесс происходит значительно медленнее, чем для других волн. При Q=100 видно, что спектральная плотность для большего числи слоёв (рис.17) для обратной волны больше, чем у прямой волны, хотя и меньше чем в периодической системе (рис.14б) ),. Возможность дальнейшего увеличения амплитуды обратной волны по сравнению с прямой волной требует дополнительных исследований. Варьируя параметры слоев и их количество, можно ожидать существенное выделение обратной волны.
|
|
|
Рис. 16. Псевдопериодическая система с
числом слоев |
|
|
|
Рис. 17. Псевдопериодическая система
с числом слоёв |
Заключение
Разработан комплекс программ, моделирующий на ПК распространение плоских электромагнитных волн в псевдопериодических средах и позволяющий найти распределение амплитуд и фаз волн по слоям при произвольном числе слоёв. Для ускорения расчетов применен метод решения получающейся системы линейных алгебраических уравнений высокого порядка, аналогичный методу прогонки. Существенным отличием разработанного комплекса является также возможность пространственного Фурье-анализа найденного распределения электромагнитного поля. Комплекс был применён для поиска псевдопериодических слоистых сред в два этапа. Сначала рассматривалась периодическая двухступенчатая среда с двумя слоями диэлектрика на периоде. Найдено сочетание толщины слоёв и их диэлектрической проницаемости, при котором получается наибольшая обратная пространственная гармоника волны при наличии интенсивной прямой гармоники. Далее для подавления прямой волны при сохранении обратной пространственной гармоники изменялась диэлектрическая проницаемость от периода к периоду. При выборе линейного закона изменения найдены варианты с преобладанием обратной волны над прямой. При дальнейших исследованиях необходимо рассмотреть и другие законы изменения, а также многоступенчатые периодические среды в качестве исходных.
Работа выполнена при финансовой поддержке Научного фонда Национального исследовательского университета «Высшая школа экономики» и Российского фонда фундаментальных исследований (проект №14-02-01013).
Литература
1. Солнцев В.А. «Плоские спиральные системы с постоянной радиальной фазовой скоростью волн» РЭ. 1994. Т. 39. № 4. С.552
2.В.А. Солнцев Псевдопериодические волноводы с селекцией пространственных гармоник и мод, Радиотехника и электроника, т. 43, № 11, 1998, с. 1285-1290.
3. В.А. Солнцев, Д.Ю. Никонов. Пространственная и частотная селекция волн в псевдопериодических замедляющих системах. Радиотехника и электроника, т. 51, № 8, 2006 , с. 1008-1018.
4. Силин Р.А. О дисперсионных свойствах двухмерно- и трехмерно периодических систем (искусственные диэлектрики) // Радиотехника и электроника 1960. - Т.5, вып.4. - С.688 - 691. Silin R.A. On dispersion properties of two- and three-periodical decelerating structures. // Journal of Communications Technology and Electronics. 1960. № 4. Pp. 983 - 991
5. С.Е. Банков Электромагнитные кристаллы.-М.: ФИЗМАТЛИТ,2010.
6. Мухин С.В., Ломакин О.Е., Солнцев В.А. // РЭ. 1988. Т.33. №8. С.1637