| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 4 , 2000 |
МЕТОД ФРАКТАЛЬНОЙ КЛАССИФИКАЦИИ СЛОЖНЫХ СИГНАЛОВ
Ю.Н. Кликушин
Омский государственный технический университет
Получена 24 марта 2000 г.
Описан метод, позволяющий классифицировать на одной фрактальной плоскости стационарные, нестационарные и квазипериодические сигналы. Представлены результаты моделирования сложных сигналов и измерения их характеристик с помощью специальных порядковых шкал, построенных на базе предложенного метода.1. Теоретические основы (R/R) – метода
Для того, чтобы иметь возможность сравнивать фрактальные свойства различных природных процессов, таких, как сток рек, отложение ила или рост колец деревьев, Херст
[1] использовал при анализе временных рядов наблюдений безразмерный показатель в виде отношения размаха (R) накопленного отклонения от среднего к среднеквадратическому отклонению (S) – (R/S) метод.Зависимость параметра (R/S) от времени наблюдения, построенная в двойном логарифмическом масштабе, представляет исследуемый процесс в виде фрактальной функции. При аппроксимации фрактальной функции прямой линией определяется угловой коэффициент Н, называемый показателем Херста. Показатель Херста используют для вычисления основного фрактального параметра процесса – размерности Хаусдорфа-Безиковича:
Размерность Хаусдорфа-Безиковича или фрактальная размерность является интегральной характеристикой объекта или процесса. Она обобщает понятие евклидовой геометрической размерности и, в отличие от последней, может принимать нецелочисленные значения.
Познавательная сила понятия фрактальной размерности состоит в том, что с его помощью можно упорядочивать исследуемые процессы по свойствам хаотичности или сложности и, таким образом, классифицировать (разделять) их. Теоретическое обобщение эмпирического метода Херста было проведено Б.Мандельбротом на основе анализа обобщенного броуновского движения в виде модели:
где:
a – некоторая постоянная, N – текущее значение объема выборки, Н – показатель Херста, принимающий значения от 0 до 1.Классификационные свойства фрактального показателя Н в методе Херста-Мандельброта иллюстрирует рис.1, на котором прямыми линиями изображены границы особых областей фрактальной плоскости, образованной координатами:
X=LOG(R/S), Y=LOG(N). Процессы, фрактальные линии которых расположены в области, где 0<H<0.5, называются антиперсистентными (пунктирная линия В) и для них характерна знакопеременная тенденция в сочетании с относительно высоким уровнем зашумленности. Процессы, фрактальные линии которых расположены в области, где 0.5<H<1, называются персистентными (пунктирная линия F) и для них характерно сохранение наблюдаемой тенденции в сочетании с относительно низким уровнем зашумленности. При H=0.5 имеют место процессы, в которых тренд отсутствует, а степень зашумленности определяется факторами, которые нельзя учесть в методе Херста-Мандельброта. В частности, фрактальные линии всех стационарных сигналов вырождаются в прямую с H=0.5 и, таким образом, никак не разделяются.Рис.1. Фрактальная плоскость (R/S) метода с примерами фрактальных линий персистентного (F) и антиперсистентного (В) процессов
Рис.2. Типовые реализации фрактальных временных рядов наблюдений c H=0.1; H=0.5; H=0.9 и белого шума с нормальным распределением
Общие закономерности связи степени зашумленности сигналов и их фрактальных свойств, выраженных показателем Херста Н, проиллюстрированы на рис.2, где изображены реализации временных рядов наблюдений (объем выборки N=1000), имеющие существенно различные фрактальные свойства и, соответственно, разные оценки показателя Херста.
Визуально можно определить, что стационарные случайные сигналы (например, шум с нормальным распределением) имеют максимальную зашумленность, а зашумленность фрактальных сигналов падает с увеличением показателя Н Херста.
Метод виртуальных объемов (МВО), наоборот, отличается тем, что хорошо разделяет стационарные случайные сигналы по форме их распределения вероятностей. Это позволяет строить специальные порядковые измерительные шкалы [2,3] и использовать их для оперативного решения задач измерений, контроля и диагностики. В отличие от метода Херста, в методе виртуальных объемов измеряется отношение размаха сигнала к среднеквадратическому отклонению.
Естественно предположить, что компиляция методов Херста и виртуальных объемов может быть полезной для построения универсальной шкалы, в которой единообразно, но раздельно представляются как стационарные, так и нестационарные сигналы.
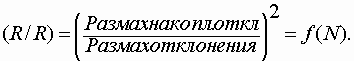
Суть предложения сводится к тому, чтобы исследовать свойства особых фрактальных (R/R) функций, представляющих собой зависимости квадрата отношения размаха накопленного отклонения от среднего к размаху отклонения от среднего, от времени наблюдения (объема выборки) N:
В качестве первого приближения, для аналитического описания указанных зависимостей предлагается использовать степенную модель вида:
где:
A, B, C – коэффициенты, зависящие от типа исследуемого процесса.Задача исследований сводится, таким образом, к установлению логической связи между совокупностью численных оценок классификационных параметров
A, B и С модели (3) и интегрированной, качественной характеристикой процесса, выраженной, например, в виде собственного имени этого процесса.2. Результаты измерения (
R/R) методом стационарных случайных сигналовМетодика измерения стационарных случайных сигналов заключалась в следующем. С помощью программных генераторов формировались выборки случайных чисел. От каждого генератора анализировалось по L – реализаций, объема N. Для каждой реализации вычислялась фрактальная (R/R) функция и оценивались параметры A, B и С ее степенной модели (3). Эти параметры усреднялись по числу реализаций, в результате чего формировались индивидуальные модельные коэффициенты, которые сопоставлялись с именем соответствующего программного генератора. В свою очередь, имя генератора совпадало с именем распределения вероятности, которому подчинялись случайные числа, извлекаемые из этого генератора.
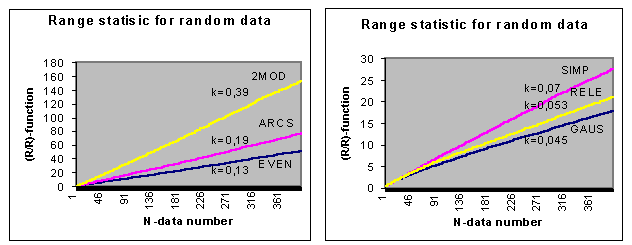
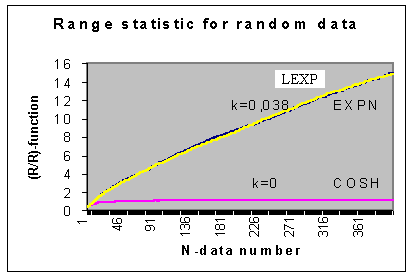
На рис.3 представлены усредненные по 1000 реализациям зависимости показателя (R/R) от объема выборки для стационарных сигналов с различной формой распределения вероятностей.
а) б)
в)
Рис.3. Фрактальные
(R/R) функции стационарных случайных сигналов с различными распределениями вероятности (а – 2МОД, АРКС и РАВН; б – СИМП, РЕЛЕ и НОРМ; в – ЛЭКС, ЭКСП и КОШИ)Вид полученных графиков четко указывает на линейный характер фрактальных функций
(R/R)=f(N), по крайней мере в пределах рассматриваемого диапазона объемов выборки N=400. Естественно, что в данных условиях, в качестве упорядочивающего идентификационного параметра проще всего взять коэффициент наклона фрактальной (R/R) линии к оси абсцисс – параметр B, т.к. при этом параметр С для всех распределений будет равен 1.По аналогии с методом виртуальных объемов параметру
B можно придать физический смысл коэффициента передачи некоторой линейной электрической цепи, на входе которой действует входная величина N, а на выходе – величина, равная NF=max(R/R). Однако, в отличие от МВО, фрактальные зависимости в (R/R) методе линейны, что упрощает построение классификационной шкалы распределений.В табл.1 представлены результаты анализа метрологических характеристик фрактальной идентификационной шкалы (ФИШ), основанной на
(R/R) – методе. В качестве оцениваемых параметров были приняты: средние значения для max(R/R) и B, систематическая погрешность (абсолютная и относительная) модели и случайная погрешность (абсолютная и относительная) для коэффициента B при уровне доверительной вероятности 95%.|
Вид распределения |
Max |
Оцифр отмет-ки |
B |
D B |
d B,% |
D cB |
g B,% |
|
153,03 |
150 |
0,3845 |
0.002 |
0,52 |
0,0769 |
20 |
|
|
АРКС |
76,959 |
75 |
0,1934 |
0.002 |
1,03 |
0,0424 |
21,9 |
|
РАВН |
50,971 |
50 |
0,1281 |
0.0005 |
0,39 |
0,0284 |
22,2 |
|
СИМП |
27,588 |
28 |
0,0693 |
0.0009 |
1,298 |
0,0133 |
19,2 |
|
РЕЛЕ |
21,013 |
21 |
0,0528 |
0.001 |
1,89 |
0,0125 |
23,8 |
|
НОРМ |
17,845 |
18 |
0,0448 |
0.0008 |
1,78 |
0,0099 |
22,2 |
|
ЛЭКС |
14,965 |
15 |
0,0376 |
0.0006 |
1,595 |
0,0080 |
21,25 |
|
ЭКСП |
14,849 |
15 |
0,0373 |
0.0005 |
1,340 |
0,0082 |
21,87 |
|
КОШИ |
1,0956 |
1 |
0,0028 |
0.0001 |
3,63 |
0,0202 |
733,9 |
Случайная погрешность, составляющая » 25%, на порядок и более превышает систематическую погрешность (1.6%). Поэтому можно округлить до целых значений оценки для max(R/R) и использовать эти оценки в качестве "оцифрованных" отметок шкалы при работе с постоянным объемом выборки N=400. Если же измерения предполагается вести в условиях, когда объем выборки может варьироваться, то рекомендуется использовать шкалу, оцифрованную в значениях углового коэффициента
B (табл.2).|
КОШИ |
ЭКСП |
ЛЭКС |
НОРМ |
РЕЛЕ |
СИМП |
РАВН |
АРКС |
2МОД |
|
|
Max(R/R) |
1 |
15 |
15 |
18 |
21 |
28 |
50 |
75 |
150 |
|
B |
0.00 |
0.04 |
0.04 |
0.045 |
0.05 |
0.07 |
0.13 |
0.2 |
0.4 |
Как и ожидалось, полученная ФИШ имеет обратную к шкале МВО упорядоченность имен распределений вероятности. Таким образом, для стационарных сигналов степенная модель переходит в линейную (параметр С модели равен 1), а разделение сигналов осуществляется с помощью коэффициента B, характеризующего упорядоченную систему распределений вероятностей.
3. Результаты измерения (
R/R) методом смеси периодического и стационарного случайного сигналовВ данном случае моделью входного сигнала является аддитивная смесь периодического сигнала и стационарного шума. Такая модель входного сигнала очень широко используется в задачах обнаружения и фильтрации полезных периодических сигналов на фоне шумов и помех.
Методология исследований основывается на измерении отклонений показаний по фрактальной шкале (
R/R) метода в зависимости от отношения сигнал-шум аддитивной смеси детерминированного периодического сигнала и стационарного шума с нормальным распределеним. В данном случае под отношением сигнал-шум (ОСШ) понимается отношение мощностей периодического и стационарного случайного сигналов.Представленные на рис.4 и 5 графики, иллюстрируют характерное поведение (
R/R)-функции при изменении отношения сигнал-шум, когда длительность интервала наблюдения не превышает половины периода детерминированного сигнала. В табл.3 приведены численные оценки коэффициентов A, B, C степенной модели для данного случая.Основной вывод, который следует из сравнительного анализа результатов моделирования, заключается в том, что наличие трендовых компонент в исследуемом сигнале идентифицируется в (
R/R) методе увеличением значения показателя степени С модели с 1 – для малых значений ОСШ, до примерно 2 – для ОСШ, равного 1. Таким образом, (R/R) метод может быть использован для выявления эффектов нестационарности исследуемых сигналов.Корреляция роста фрактального показателя С и ОСШ наблюдается для всех исследованных смесей, кроме тех, в которых случайная компонента имеет распределение (табл.2), КОШИ
.Особенность фрактальных
(R/R)-линий для периодических сигналов, когда длительность интервала наблюдения превышает период детерминированной составляющей, заключается в наличии уровня ограничения. Это непосредственно сказывается на значении фрактального показателя С, который становится меньше 1.В качестве примера на рис.
6 показана фрактальная (R/R)-функция выбрки синусоидального сигнала с 3-мя периодами. Оценка значения фрактального показателя С для такого сигнала составляет 0.38.Данное обстоятельство можно использовать для обнаружения скрытых периодичностей.

Рис.4. Пример (R/R)-функции смеси стационарного шума с НОРМ распределением и полупериода гармонического сигнала: ОСШ=0.1
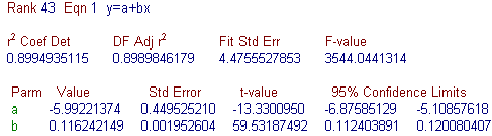
Рис.5. Пример (R/R)-функции смеси стационарного шума с НОРМ распределением и полупериода гармонического сигнала: ОСШ=0.25
|
НОРМ распределение |
Параметры степенной модели y=a+bxc фрактальных линий и их погрешности |
|||||
|
A |
D A |
B |
D B |
C |
D C |
|
|
ОСШ=0.1 |
0.81 |
± 0.21 |
0.038 |
± 0.006 |
1.08 |
± 0.03 |
|
ОСШ=0.25 |
1.38 |
± 0.22 |
0.010 |
± 0.001 |
1.43 |
± 0.02 |
|
ОСШ=0.5 |
1.86 |
± 0.32 |
0.009 |
± 0.001 |
1.62 |
± 0.01 |
|
ОСШ=1.0 |
2.80 |
± 0.65 |
0.011 |
± 0.001 |
1.74 |
± 0.02 |
Рис.
6. Пример фрактальной (R/R)-функции для выборки синусоидального сигнала с 3-мя периодамиОсобенность примера рис.7 состоит в том, что анализируемый сигнал 99 моделирует шум морского прибоя. Этот шум содержит периодическую компоненту, связанную с движением волн. Поскольку период наката волн на берег непостоянен, фрактальная линия на рис.7, б размыта. Однако, среднее значение фрактальной траектории совершенно четко указывает на сублинейный (С
<1, C = 0.23) характер имеющихся вариаций, сигнализируя о наличии фрактальной периодической закономерности.Если данные рассуждения, в отношении свойств периодичности, справедливы хоть отчасти, то появляется возможность связать значения фрактального параметра С степенной модели с числом периодов образцового гармонического сигнала и, таким образом, не только выявлять, но и оценивать периодичность сигналов. На рис.8 представлена зависимость фрактального показателя С от числа периодов синусоидального сигнала в аддитивной смеси с нормальным шумом. Замечательная особенность этой зависимости состоит в том, что, если время наблюдения совпадает с длительностью периода, фрактальный показатель С достигает максимума. Это свойство может быть использовано для формирования оптимизационных алгоритмов измерения длительности периода полезного сигнала в условиях значительной его зашумленности (когда ОСШ мало).
В частности, для примера с сигналом 99 оценка времени наблюдения, при которой фрактальный показатель С достигает максимума, равного 3.23, полученная методом последовательных приближений, составила
Nt = 117 отсчетов. Другой метод вычисления оценки Nt длительности скрытого периода состоит в совместном решении системы уравнений, определяющей равенство угловых коэффициентов хорды и касательной фрактальной (R/R) функции:a)
б)
Рис.7. Пример сублинейной (С<1) фрактальной (R/R)-функции (б) для выборки случайного сигнала 99 (а)
Рис.8. Зависимость фрактального параметра С(k) степенной модели (R/R)-функции аддитивной смеси сигнала с шумом от числа k периодов гармонического сигнала (ОСШ=0.1)
В уравнении (4): В и С – оценки параметров модели (3), К – угловой коэффициент хорды, соединяющей начальную и конечную точки (
R/R) функции, равный max(R/R)/max(N). Подстановка в (4) численных оценок параметров В=5.2; С=0.23 и К=13/400=0.03, дает: Nt=120. Следовательно, оба метода вычисления скрытой периодичности дают близкие результаты.Таким образом, параметр С степенной модели
(R/R) фрактальных линий служит переключателем типа исследуемого процесса следующим образом. При С=1 имеет место стационарный шум, фрактальные линии которого линейны, а вид распределения вероятностей идентифицируется коэффициентом наклона этих линий к оси абсцисс. Если С>1, значит во входном сигнале присутствует трендовая компонента. Когда С<1, фрактальные линии имеют уровень насыщения, а сигнал, соответственно, содержит явные или скрытые периодические составляющие. Эти составляющие могут быть оценены даже при малых уровнях отношения сигнал-шум, используя "резонансный" характер зависимости фрактального показателя С от соотношения длительности скрытого периода и времени наблюдения.Рассмотренная технология была использована для построения системы виртуальных анализаторов, обладающих большим динамическим диапазоном измерения форм сигналов. Соответствующее программное обеспечение можно получить на сервере Омского государственного технического университета:
http//www.omgtu.omskelecom.ru/~lab308 –
страница лаборатории Интеллектуальных систем измерения, контроля и диагностики при кафедре "Информационно-измерительная техника".ЛИТЕРАТУРА
Автор:
Кликушин Юрий Николаевич, доцент кафедры Информационно-измерительная
техника" Омского государственного
технического университета
Адрес: 644050, Омск-50, пр.Мира, 11,
ОмГТУ