"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 4 , 2000

оглавление

дискуссия

АНАЛИЗ РАССЕИВАЮЩИХ СВОЙСТВ НЕСФЕРИЧЕСКИХ ЧАСТИЦ В СЛОИСТОЙ СТРУКТУРЕ

Е.Ю. Еремина, А.Г. Свешников

Московский государственный университет им. М.В. Ломоносова,
Физический факультет

Получена 20 апреля 2000 г.

Работа посвящена разработке и реализации метода анализа рассеивающих свойств несферических проницаемых частиц, расположенных под поверхностью пленки, нанесенной на подложку. В качестве основы использован метод дискретных источников. Обсуждаются результаты моделирования, связанные с рассеивающими свойствами сфероидальных частиц. 

Прогресс в микроэлектронике приобретает в последние годы все более динамичный характер. Особенно это заметно в областях производства микропроцессоров для современных персональных компьютеров, элементов памяти и жестких дисков, а также совершенствовании схем сотовых телефонов и системных плат дисплеев. По мере миниатюризации и усложнения объемных интегральных схем проблема обеспечения чистоты их изготовления становится все более актуальной. Одним из аспектов стандартизации чистоты является проблема обнаружения загрязняющих частиц, попадающих на поверхность кремниевого вейфера на различных стадиях технологического процесса формирования интегральной схемы. Обнаружение загрязняющих частиц на вейфере осуществляется с помощью оптических поверхностных сканеров, конструкция которых включает в себя лазерный источник излучения и систему коллекторов рассеянного частицей излучения. Совершенствование конструкций поверхностных сканеров представляет приоритетную задачу для разработчиков и производителей измерительного оборудования для производства объемных интегральных схем [1].

Одним из возможных путей разработки конструкций интеллектуальных сканеров является использование средств математического моделирования процессов рассеяния электромагнитного излучения частицей на слоистой подложке. В настоящее время наиболее сложной и трудно поддающейся разрешению проблемой является обнаружение и идентификация микрочастиц, скрытых под пленкой, которая используется в процессе литографии кремниевых подложек. Проведение экспериментальных исследований осложняется отсутствием технологии калибровки частиц, за исключением полистироловых, и требует больших денежных затрат. В работе [2] , на основе метода дискретных источников (МДИ), проводился анализ рассеяния P/S поляризованного света частицами и ямами на кремниевой подложке. В работе [3] развитая методика была распространена на случай осесимметричной частицы, расположенной под пленкой на подложке. Однако вопрос о влиянии деформаций, ведущих к неосесимметричным структурам, на рассеивающие свойства микрочастиц практически не рассматривался. В данной работе проводится обобщение МДИ на случай произвольной проницаемой частицы, расположенной в слое на поверхности подложки. Особый интерес представляет тот случай, когда несферическая частица плюс слоистая подложка вместе уже не образуют осесимметричной структуры. На основе компьютерной реализации развитого подхода проводится анализ рассеивающих свойств эквиобъемных частиц различных геометрий. Установлено, что отклонение от сферической формы, в основном, приводит к снижению уровня рассеянного излучения.

Начнем с математической постановки рассматриваемой задачи. Пусть - поле плоской электромагнитной волны линейной поляризации, падающей под углом относительно нормали на плоскую границу раздела воздух-слой , а частица, занимающая область с гладкой границей , расположена целиком внутри слоя, ограниченного плоскостями и . Плоскость разделяет слой и подложку. Введем прямоугольную систему координат, выбрав ее начало на плоскости . Ось Oz направим вдоль нормали к подложке в область . Тогда математическая постановка задачи рассеяния принимает вид

условия излучения/затухания для рассеянных
полей на бесконечности (z ¹ 0,d).                                                                                                           (2.1д)

Здесь x – векторное произведение, - полное поле в соответствующей области , , а - нормаль к поверхности . Полагаем, что поверхность частицы является гладкой , а параметры сред удовлетворяющими условиям (временная зависимость выбрана в виде ). Тогда граничная задача (2.1) имеет единственное решение.

Прежде чем строить приближенное решения для рассеянных полей решим задачу дифракции поля плоской волны на слоистой структуре: воздух-слой-подложка. Как известно, это решение может быть записано в явном виде. Будем обозначать полученное поле . Пусть есть рассеянное поле в . Будем строить приближенное решение задачи (2.1) на основе базовой концепции МДИ, развитой в [4]. В данном случае, суть МДИ состоит в представлении для поля в виде конечной линейной комбинации полей диполей, которая удовлетворяет системе уравнений Максвелла в областях , условиям на бесконечности для рассеянного поля в , а также условиям сопряжения для тангенциальных компонент полей на . В этом случае решение граничной задачи рассеяния (2.1) сводится к задаче аппроксимации поля внешнего возбуждения на поверхности частицы полями диполей. Таким образом, определение неизвестных амплитуд ДИ производится из условий сопряжения для полей только на поверхности частицы:

Поскольку рассматриваемая структура частица-подложка более не является осесимметричной, то нет возможности использовать подход столь успешно реализованный в [3].

В основу представления для рассеянного частицей поля положим источники электрического типа, удовлетворяющие условиям сопряжения для полей на поверхностях . В этом случае поля выражаются через векторные потенциалы следующим образом

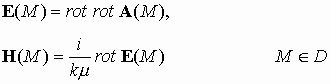
где векторный потенциал с точностью до нормирующего множителя принимает вид

Здесь - тензор Грина слоистой среды [5]

При этом для компонент тензора Грина справедливы следующие представления, включающие интегралы Зоммерфельда

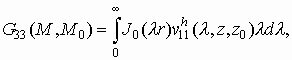
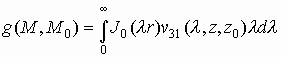                                                                                          (2.5а)

здесь - цилиндрическая функция Бесселя, , - цилиндрические координаты точки . В данном случае для спектральных функций имеют место представления:

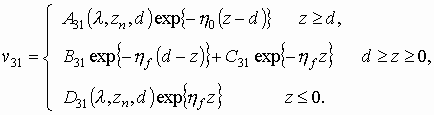                                                   (2.5б)

Решая задачу удовлетворения условиям сопряжения на границах z=0, d

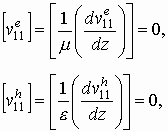
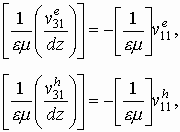
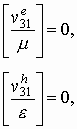
получим выражения для коэффициентов:

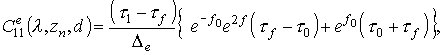                                                   (2.5в)

, , 

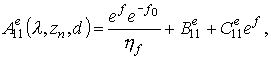
здесь . Выражения для получаются заменой на в формулах для .

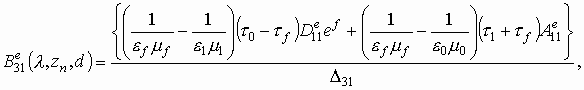
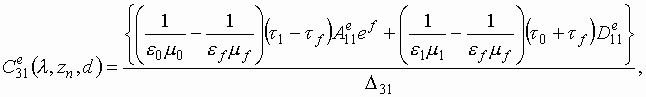
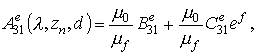
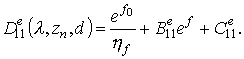
Переход от к осуществляется посредством замены на , на . Поскольку и инвариантны к подобному переходу, то 

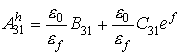Таким образом спектральные функции (2.5б) с соответствующими коэффициентами (2.5в) обеспечивают выполнение условий сопряжения на границе z=0, d .

Будем строить представление для рассеянного поля в на основе системы электрических диполей, локализованных в точках , которые распределены всюду плотно на вспомогательной поверхности . Поверхность располагается строго внутри . Будем полагать, что в каждой точке располагаются три линейно независимых диполя . Пусть диполи ориентированы в соответствии с локальной цилиндрической системой координат с началом в . В соответствии с (2.3), потенциалы, соответствующие каждому такому диполю, имеют вид

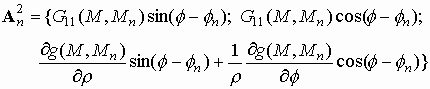                                                    (2.6)

Здесь соответствует диполю в точке , ориентированному по , - , - .

Итак, для рассеянного поля в , удовлетворяющего условиям сопряжения на границах , справедливо следующее представление

Приступим теперь к построению приближенного решения внутри проницаемой частицы . Введем в рассмотрение следующую систему векторных потенциалов

здесь - сферическая функция Бесселя. Тогда представление для полного поля внутри частицы принимает вид

Как уже отмечалось ранее, представление (2.7), (2.9) удовлетворяет всем условиям граничной задачи (2.1) за исключением условий сопряжения на поверхности частицы (2.2). Введем в рассмотрение вектор амплитуд ДИ , который будем определять из условия

Используя свойство полноты системы электрических диполей, всюду плотно расположенных на вспомогательной поверхности и теорему корректности [4], можно показать сходимость в равномерной норме приближенного решения (2.7), (2.9) к точному решению задачи (2.1) в любом компакте

Изложим кратко схему вычислительного алгоритма. Как уже отмечалось ранее, поле внешнего возбуждения, входящее в правую часть (2.2) , может быть получено в явном виде. Как уже отмечалось выше, определение вектора амплитуд ДИ проводится из требования приближенного выполнения с заданной точностью в норме условий сопряжения (2.2). Для приближенного решения задачи минимизации (2.10) используем обобщенный метод коллокаций [4]. Для этого выберем на поверхности частицы множество точек коллокаций , равномерно покрывающих поверхность целиком. Амплитуды дискретных источников, локализованных на вспомогательной поверхности внутри рассеивателя, определяем, решая полученную переопределенную систему линейных уравнений с матрицей размерности . Как и в осесимметричном случае, МДИ предоставляет возможность апостериорной оценки точности полученного решения посредством вычисления невязки на поверхности частицы в среднеквадратичной норме.

Отметим характерные отличия настоящего подхода от рассмотренного ранее случая осесимметричной структуры [3] . Основное состоит в том, что приближенное решение в данном случае не зависит от поляризации внешнего возбуждения. Это позволяет решать задачу рассеяния сразу для всего набора углов падения и двух поляризаций. Кроме того, в представление для рассеянного поля (2.7) входят лишь дипольные источники, а не мультиполи [3]. Последнее обстоятельство существенно облегчает расчет интегралов Зоммерфельда, что делает схему вычисления амплитуд более устойчивой.

Как и в осесимметричном случае, для вычисления интенсивности рассеянного поля на бесконечности необходимо иметь диаграмму рассеяния. Она определяется как:

.

Для получения конкретного вида диаграммы рассеяния достаточно использовать асимптотические представления для интегралов Зоммерфельда

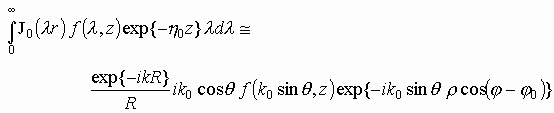
Тогда для - компонент диаграммы рассеяния получим

Здесь - цилиндрические координаты точки , а спектральные функции имеют вид

Таким образом, компоненты диаграммы рассеяния не содержат интегралов Зоммерфельда, и после определения неизвестных амплитуд дискретных источников для расчета характеристик рассеяния достаточно вычислить лишь комбинацию элементарных функций.

Загрязняющие микрочастицы, обладают широким набором веществ. Так как размеры частиц существенно меньше длины волны лазерного излучения и в сотни раз меньше диаметра лазерного пятна, модель P или S поляризованной плоской волны является приемлемой моделью внешнего возбуждения. В настоящее время поверхностные сканеры способны обнаруживать микрочастицы полистирола с эквиобъемным диаметром до 0,05мкм [1]. Наиболее распространенная длина волны лазера l =0,488мкм. Подобные микрочастицы часто называют “релеевскими” и используют в качестве модели подобной частицы эквиобъемный сферический шарик. Большинство результатов, положенных в основу современных конструкций поверхностных сканеров основано на анализе рассеивающих свойств сферических частиц.

В настоящей работе в качестве основной исследуемой характеристики рассеяния рассматривается интенсивность рассеяния

где - компоненты диаграммы рассеяния (3.1), соответствующие P/S поляризации возбуждающей плоской волны. Размерность интенсивности (4.1) – мкм². Также вычисляется интегральный поперечник рассеяния

здесь телесный угол .

Будем рассматривать микрочастицы сфероидальной формы, большая ось которых параллельна подложке. При этом малая ось должна быть меньше толщины слоя, то есть частица целиком расположена в слое. Будем полагать, что все частицы эквиобъемны сфере диаметром D=0.05мкм. толщина слоя во всех расчетах взята равной d=0.18мкм. Мы будем рассматривать два варианта расположения частицы по отношению к плоскости падения (ZX): когда большая ось сфероида параллельна плоскости падения (конфигурация ZX), и когда большая ось перпендикулярна плоскости падения (конфигурация ZY). Будем полагать, что подложка выполнена из кремния с индексом рефракции равным 4,37-0,08i, а пленка из оксида кремния с индексом рефракции 1,46. Здесь и далее приведены индексы рефракции, соответствующие длине волны l =0,488мкм.

В работе [7] было предложено использовать другую аппроксимацию для частиц несферической формы: вместо сферы эквиобъемного диаметра D=0.05мкм используется сфера, диаметр которой вычисляется по формуле D=6V/S. Подобная аппроксимация, в случае рассеяния на несферических частицах в свободном пространстве, давала гораздо лучшее приближение.

Во всех приведенных ниже рисунках показана только Р-поляризация, так как большинство современных конструкций оптических сканеров используют именно этот источник излучения [1].

На рисунках 1а,б приведена зависимость интегрального поперечника рассеяния от угла падения. Рисунок 1а соответствует кремниевому сфероиду с отношением осей (b/a) равным 2. Представлены две кривые для различных конфигураций (ZX, ZY). Для сравнения дана кривая, соответствующая сфере эквиобъемного диаметра D=0.05мкм, и кривая, соответствующая сфере диаметра D=6V/S=0.0464мкм. На рисунке 1б приведены аналогичные результаты для частицы из вольфрама (3,36-2,66i). Из рисунков видно, что для наиболее часто используемых в сканерах углах возбуждения () обе аппроксимации являются приемлемыми, причем для конфигурации ZX лучше подходит сфера диаметра D=0.05мкм, а для ZY сфера диаметра D=0.0464мкм.

На рисунках 2а,б приведено сравнение рассеянных интенсивностей в плоскости падения для сфероида (b/a=2) и сферических частиц D=0.05мкм, D=6V/S в зависимости от угла наблюдения. Рисунок 2а соответствует кремниевой частице, а 2б частице из вольфрама. Данные результаты иллюстрируют сильную зависимость интенсивности от формы микрочастицы. В частности в случае ZX конфигурации практически отсутствует характерный для сферических аппроксимаций провал кривой в районе нуля градусов.

На рисунке 3а,б приведен интегральный поперечник рассеяния в зависимости от соотношения осей сфероида при угле падения . Две кривые соответствуют различным конфигурациям сфероида, а две другие – сферическим частицам D=0.05мкм, D=6V/S. Рисунок 3а относится к кремниевой частице, 3б - к вольфрамовой. Из рисунков видно, что предложенные аппроксимации приемлемы лишь при небольших деформациях (приблизительно до соотношения b/a=1.75).

Кремний : 1 - ZX, 2 - ZY, 3 - сфера D=0.05мкм, 4 - сфера D=6V/S.

Рис. 1б.

Вольфрам : 1 - ZX, 2 - ZY, 3 - D=0.05мкм, 4 - D=6V/S.

Рис. 2а.

Кремний : 1 - ZX, b/a=2; 2 – ZY, b/a=2, 3 - D=0.05мкм, 4 - D=6V/S.

Вольфрам : 1 - ZX, b/a=2; 2 – ZY, b/a=2, 3 - D=0.05мкм, 4 - D=6V/S.

Кремний : 1 - ZX, 2 – ZY, 3 - D=0.05мкм, 4 - D=6V/S.

Вольфрам : 1 – ZX, 2 – ZY, 3 – D=0.05мкм, 4 – D=6V/S.

Кремний : 1 – b/a=1; 2 – b/a=1.5, 3 - b/a=2, 4 - b/a=2.5.

Вольфрам : 1 – b/a=1; 2 – b/a=1.5, 3 - b/a=2, 4 - b/a=2.5.

Время расчета для сфероидальной вольфрамовой частицы с соотношением осей 1:2 диаметром 0.05 мкм на PC Pentium-II 400 составило 4 минуты. При этом достижение невязки в норме 4% гарантировало погрешность расчета интенсивности менее 2%.

Предложен и реализован эффективный алгоритм анализа рассеивающих свойств неосесимметричных структур в пленке на подложке, позволяющий проводить апостериорную оценку точности окончательных результатов. Проведенный вычислительный эксперимент выявил существенную зависимость рассеянной интенсивности от формы (ориентации) несферической микрочастицы и позволил оценить границы применимости различных сферических аппроксимаций. 

СПИСОК ЛИТЕРАТУРЫ

1. Baliga J. Defect detection on patterened wafers//Semiconductor International. 1997. N4, pp 64-70.
2. Еремин Ю.А., Орлов Н.В. Свешников А.Г. Идентификация дефектов силиконовых подложек в устройствах микроэлектроники методом дискретных источников//Электромагнитные волны. 1998. №5. Стр. 34-43.
3. Еремина Е.Ю., Свешников А.Г. Анализ рассеяния света частицей внутри слоя на основе метода дискретных источников//Вестник Московского Университета. Сер.3. Физика. Астрономия. 1999. №1. Стр.12-17.
4. Еремин Ю.А., Свешников А.Г. Метод дискретных источников в задачах электромагнитной дифракции. - М.: Изд-во МГУ, 1992.
5. Дмитриев В.И. Поля в слоистых средах. - Изд-во МГУ, 1963.
6. Фелсен Л., Маркувиц Н. Излучение и рассеяние волн. Т. 1. - М.: Мир, 1978.
7. Grenfell T.C. and Warren S.G. Representation of a nonspherical ice particle by a collection of independent spheres for scattering and absorption of radiation//J. Geophysical Res. Vol.104, No.D24, pp.31,697-31,709, 1999.

Авторы:

Еремина Елена Юрьевна, e-mail: eremin@cs.msu.su
Свешников Алексей Георгиевич, e-mail: agsveshn@math380b.phys.msu.su
Московский государственный университет им. М.В. Ломоносова, Физический факультет.

оглавление

дискуссия