|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 4, 2002 |
|
ОПТИМАЛЬНЫЙ ПОИСК НЕПОДВИЖНОЙ ЦЕЛИ МНОГОПОЗИЦИОННОЙ
ИНФОРМАЦИОННОЙ СИСТЕМОЙ
А. А. Строцев, e-mail: jvalera@vsu.by
Ростовский военный институт ракетных войск.
Получена 10 апреля 2002 г.
В статье рассмотрена задача построения критерия оптимальности для процесса поиска неподвижного объекта многопозиционной информационной системой, обеспечивающего непосредственную реализацию управления и учёт апостериорной информации о результатах поиска.
Задачи поиска возникают в различных областях науки и её приложениях. В связи с этим существуют различные постановки задачи и определения понятия поиска. Основной целью поиска является обнаружение объектов, т.е. установление факта их присутствия в обследуемом пространстве, как правило, с определением их характера и местоположения. Часто требуется осуществить поиск неподвижной (статической) цели с помощью многопозиционной информационной системы (МИС). Подобного рода задачи рассмотрены, например, в [1]-[3]. При этом функционирование МИС представляется в виде некоторых функций, на которые наложены определённые ограничения. Эти функции с одной стороны описывают действия МИС, а с другой стороны являются искомым управлением. Так в [2] поисковая система описывается интенсивностью поиска или потенциалом обнаружения, а в [3] «большая поисковая система» описывается функцией плотности (стратегией) поиска. Однако реализация такого оптимального управления для конкретной системы является довольно трудной задачей [3]. Тем более что ограничения на возможность сосредоточения поисковых усилий в конкретной точке зоны поиска не рассматриваются или их учёт затруднён.
Отметим, что к задаче поиска статической цели можно прийти при поиске в ограниченной области (поиск на рубеже, поиск «по вызову» [2]) подвижной цели, обладающей небольшой динамикой по сравнению с возможностями МИС (например, состоящей из радиоэлектронных измерителей или при поиске наземных целей с помощью МИС воздушного базирования [4]).
Важным вопросом при синтезе оптимального управления поиском является выбор методологического подхода к решению этой задачи: априорного или апостериорного. Применительно к решению смежных задач – фильтрации и управления наблюдениями анализ этой проблемы дан в [5]. Предпочтение следует отдать апостериорному подходу, в силу его непосредственного соответствия реальной ситуации поиска, когда поиск объекта ведётся на заданном интервале времени и получается одна реализация выходного сигнала измерительных пунктов МИС. Однако применение чисто апостериорного подхода затруднено в виду необходимости решения задачи планирования – построения плана поиска до начала поискового процесса, в связи с чем, основные работы по теории поиска лежат в русле априорного подхода.
Таким образом, синтез оптимального управления МИС на уровне отдельных устройств при поиске целей с учётом апостериорной информации о положении цели является актуальной задачей.
Рассматривается МИС, включающая центральный пункт обработки (ЦПО) и
![]() управляемых
измерительных пунктов. Не снижая общности, положим, что все измерительные
пункты являются непрерывными, уравнения наблюдения которых в режиме поиска
имеют вид
управляемых
измерительных пунктов. Не снижая общности, положим, что все измерительные
пункты являются непрерывными, уравнения наблюдения которых в режиме поиска
имеют вид
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() -
вектор формирующих белых гауссовских шумов с нулевыми математическими
ожиданиями и единичными интенсивностями,
-
вектор формирующих белых гауссовских шумов с нулевыми математическими
ожиданиями и единичными интенсивностями,
![]() -
известные диагональные матрицы интенсивностей,
-
известные диагональные матрицы интенсивностей,
![]() -
случайная величина, характеризующая положение новой цели, а
-
случайная величина, характеризующая положение новой цели, а
![]() -
траекторию её поиска. Функции
-
траекторию её поиска. Функции
![]() полагаются
известными. Они характеризуют состав измеряемых параметров и зависимость их
значений от траектории поиска и положения цели. Функции
полагаются
известными. Они характеризуют состав измеряемых параметров и зависимость их
значений от траектории поиска и положения цели. Функции
![]() определяют
режим функционирования измерительных пунктов. Оптимизации подлежит совместная
траектория поиска
определяют
режим функционирования измерительных пунктов. Оптимизации подлежит совместная
траектория поиска
где
Т – знак операции транспонирования, реализующая управление поиском на
уровне отдельных измерительных пунктов. Положение искомой цели в области
![]() в
начальный момент времени задаётся априорной плотностью распределения
в
начальный момент времени задаётся априорной плотностью распределения
![]() ,
,
![]() .
Цель полагается неподвижной. Требуется на основе анализа уравнений (1.1)
ввести критерий оптимальности управления (1.2) МИС в режиме
писка, допускающий учёт апостериорной информации о положении цели, а также
определить пути нахождения (1.2), соответствующего этому
критерию оптимальности.
.
Цель полагается неподвижной. Требуется на основе анализа уравнений (1.1)
ввести критерий оптимальности управления (1.2) МИС в режиме
писка, допускающий учёт апостериорной информации о положении цели, а также
определить пути нахождения (1.2), соответствующего этому
критерию оптимальности.
3. Критерий оптимальности управления поиском
С вероятностной точки зрения наиболее полная информация о положении искомой
цели после проведения поиска содержится в апостериорной плотности
распределения
![]() .
Выражение для
.
Выражение для
![]() может
быть получено в соответствии с подходом (см., например, в [6]),
принятым при описании наблюдаемых процессов:
может
быть получено в соответствии с подходом (см., например, в [6]),
принятым при описании наблюдаемых процессов:
где
![]() -
отношение функционалов правдоподобия,
-
отношение функционалов правдоподобия,
С другой стороны, выражение апостериорной плотности распределения положения цели может быть получено в виде [3]
с
помощью т.н. функции плотности поиска (стратегии поиска)
![]() ,
которая обладает следующими свойствами:
,
которая обладает следующими свойствами:
1.
![]() для
всех
для
всех
![]() ,
,
![]() ;
;
2.
 для
всех
для
всех
![]() ;
;
3.
![]() -
есть вероятность обнаружения цели в интервале времени
-
есть вероятность обнаружения цели в интервале времени
![]() при
условии, что цель находится в точке
при
условии, что цель находится в точке
![]() и
не обнаружена до момента
и
не обнаружена до момента
![]() .
.
Приравнивая (2.1) и (2.5) несложно
показать, что для всех
![]()
где
![]() для
всех
для
всех
![]() .
.
Ясно, что по условиям рассматриваемой задачи критерий эффективности поиска должен принадлежать группе вероятностных критериев [2] (производительные критерии не позволяют учесть стохастическую сущность каналов поиска, хотя подходят для априорного, апостериорного и смешанного подходов к планированию и оценке результатов поиска).
Отметим, что вероятностные критерии позволяют оценить возможности поиска ещё
до его начала и соответствуют априорному подходу. Наибольшее распространение
из этой группы получил критерий максимизирующий вероятность обнаружения
объекта в течение заданного времени
![]() [1]-[3]
-
[1]-[3]
-
![]() .
В соответствии с [1]:
.
В соответствии с [1]:
Но тогда, учитывая (2.6) получим
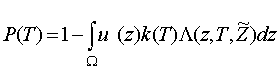 ,
,
а поскольку
![]() и
и
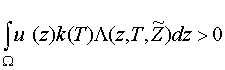 ,
то
,
то
эквивалентный критерий оптимальности можно представить в виде
Достоинства эквивалентного критерия апостериорной вероятности обнаружения объекта к заданному времени:
1. Оптимизации подлежат траектории поиска отдельных измерительных пунктов, т.е. получаемое оптимальное управление МИС в режиме поиска является легко реализуемым.
2. Оптимальные по (2.8) траекторий поиска максимизируют вероятность обнаружения объекта к заданному времени, при этом не требуется знания трудно определимых для конкретных систем функций, описывающих МИС в режиме поиска с вероятностной точки зрения (например, плотности поиска, интенсивности поиска, и т.д.). Однако при применении (2.8) значение оптимальной вероятности обнаружения объекта к заданному времени остаётся невычислимым и можно оперировать при необходимости только её относительным приращением.
3. Оптимальная по критерию (2.8) совместная траектория поиска соответствует апостериорному подходу, поскольку при определении (2.8) учитываются реализации (1.1).
4. При составлении моделей поисковых ситуаций на основе (2.8) можно учитывать ограничения на уровне отдельных измерительных пунктов, в том числе, как по времени, так и по пространству.
5. Синтез оптимального управления поиском в соответствующей поисковой ситуации по классическому критерию [3] основан на решении задачи оптимального управления с ограничениями в виде дифференциальных уравнений в частных производных. А некоторые задачи, построенные на критерии (2.8), могут быть отнесены даже к классу задач математического программирования.
4. Задачи оптимизации поиска по эквивалентному критерию апостериорной вероятности обнаружения объекта к заданному времени
На основе критерия (2.8) могут быть получены модели для
различных поисковых ситуаций. Однако следует отметить, что с помощью этого
критерия, учитывающего апостериорную информацию, можно оценить оптимальность
траектории поиска при конкретной реализации процессов
![]() ,
,
![]() ,
но осуществить планирование поиска непосредственно невозможно.
,
но осуществить планирование поиска непосредственно невозможно.
Положим, что процесс поиска формируется как последовательное чередование двух
этапов: планирования и реализации оптимального поиска. При этом для
этапа планирования применим гарантировано-стохастических подход: планирование
осуществляется в предположении, что сигнал в реализации процессов
![]() ,
,
![]() отсутствует,
и при расчёте (2.8) используется их математическое
ожидание. Таким образом, для решения задачи планирования поиска, реализуемого
на интервалах
отсутствует,
и при расчёте (2.8) используется их математическое
ожидание. Таким образом, для решения задачи планирования поиска, реализуемого
на интервалах
![]() ,
,
![]() ,
выражение (2.8) можно переписать в виде
,
выражение (2.8) можно переписать в виде
где
![]() ,
,
![]() -
для
-
для
![]() определяются
по выражению соответствующему (2.1)
определяются
по выражению соответствующему (2.1)
![]() ,
,
![]() .
.
Значения
![]() и
и
![]() выбираются
на основе анализа поисковой ситуации и ограничений на
выбираются
на основе анализа поисковой ситуации и ограничений на
![]() ,
например, вида
,
например, вида
Отметим, что при планировании поиска для последующих этапов используется апостериорная информация о результатах поиска на предыдущих.
При
применении (2.8) может быть учтён большой спектр
ограничений на
![]() ,
например,
,
например,
где
![]() ,
,
где
![]() ,
,![]() .
.
При этом в целях простоты реализации оптимальных траекторий поиска для конкретной системы, удобно получение их в виде полиномов различных степеней (для этого вводится ограничение, например, вида (3.5)).
Следовательно, для формирования оптимального управления поиском относительно максимума вероятности обнаружения цели к моменту времени Т задача должна содержать критерий (3.1), (3.2) и ограничения, например, вида (3.3)-(3.6). И, таким образом, построенная модель позволяет применить её к решению большого числа реальных поисковых ситуаций.
5. Пример задачи оптимизации поиска по эквивалентному критерию апостериорной вероятности обнаружения объекта к заданному времени
Для примера рассмотрим один этап планирования поиска
в следующей задаче:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() -
отрезок
-
отрезок
![]() ,
,
![]() ,
,
![]() ,
,
Задана априорная плотность распределения положения цели в виде
нормальной плотности распределения
![]() .
.
Требуется найти оптимальные по критерию (3.1) значения
величин
![]() .
.
В
результате решения задачи методом сопряжённых градиентов получим:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
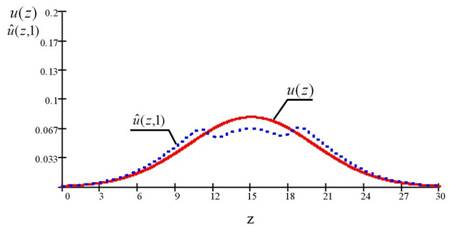
Вид априорного и апостериорного распределения положения цели в случае её отсутствия на оптимальной траектории поиска показан на рис. 1.
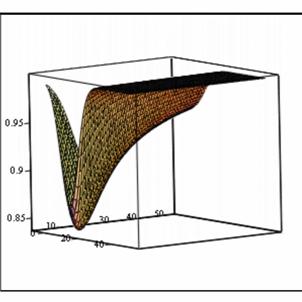
На
рис.2 показано сечение функционала (3.1)
при
![]() ,
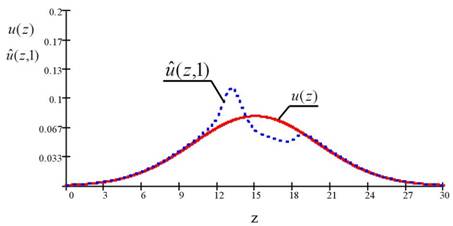
а на рис.3 вид априорного и апостериорного распределения положения цели при её
нахождении на траектории поиска (в точке
,
а на рис.3 вид априорного и апостериорного распределения положения цели при её
нахождении на траектории поиска (в точке
![]() .
.
Из анализа рис.1 видно, что полученное оптимальное управление в виде траектории поиска стремиться к равномерно оптимальной стратегии поиска [1],[3] и не достигает её из-за ограничения (4.3). Следовательно, оптимизация по критерию (3.1) эквивалентна получению равномерно оптимальных стратегий поиска, при этом имеется возможность последовательного учёта апостериорной информации о результатах поиска, а оптимальные стратегии поиска в виде траекторий поиска легко реализуемы.
В статье рассмотрены пути формирования моделей широкого круга задач оптимального поиска неподвижных объектов. Показано, что для получения адекватных моделей, позволяющих учитывать апостериорную информацию о результатах поиска и формировать легко реализуемое оптимальное управление, необходимо использовать эквивалентный критерий апостериорной вероятности обнаружения объекта к заданному времени.
1. Аркин В.И. Задачи оптимального распределения поисковых усилий. – Теория вероятностей и её применения, 1964, т. 9, № 1.
2. Абчук В.А., Суздаль В.Г. Поиск объектов. М.: Сов. радио, 1977.
3. Хеллман О. Введение в теорию оптимального поиска. – М.: Наука, 1985.
4. Керков В.Г. Скабаров М.М. Методика комплексной оценки эффективности радиолокационной системой в условиях конфликтного противодействия. – Интернет-публикация, М.: Журнал радиоэлектроники , №12, 2000.
5. Малышев В.В., Красильщиков М.Н., Карлов В.И. Оптимизация наблюдения и управления летательных аппаратов. – М.: Машиностроение, 1989.
6. Хуторцев В.В. Теоретические основы обработки сигналов и управление наблюдениями в радиотехнических системах. МО РФ, 1998.
7. Горбунов В.А. Эффективность обнаружения целей. М.: Воениздат, 1980.
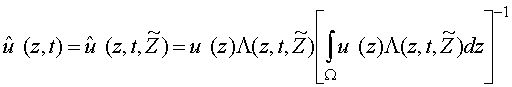
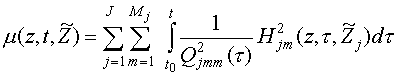 ,
(2.3)
,
(2.3) 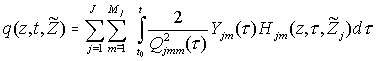 .
(2.4)
.
(2.4) 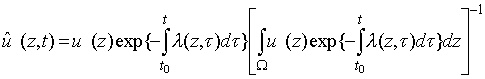
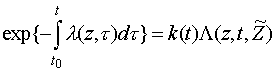
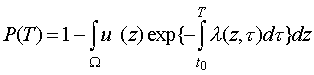
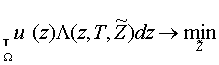
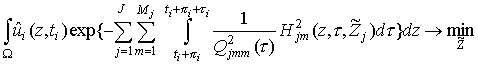
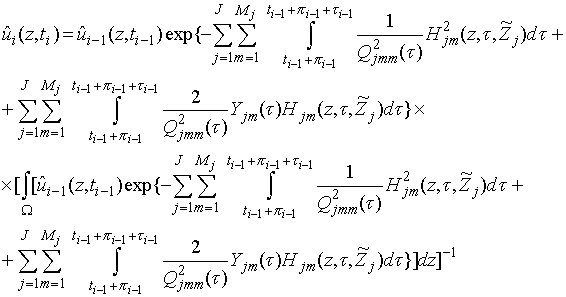
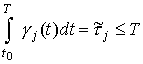 .
(3.3)
.
(3.3)