"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 4, 2004

оглавление

дискуссия

УДК 681.7.068.4

ВЛИЯНИЕ РЕЛАКСАЦИОННЫХ СВОЙСТВ МАТЕРИАЛОВ ПЕРВИЧНЫХ ПОКРЫТИЙ  НА ПРОЧНОСТЬ И ДОЛГОВЕЧНОСТЬ СВЕТОВОДОВ.

А.А. Дяченко^©, О.Е. Шушпанов^©, Л.П. Прокофьева^§, В.В. Щербаков^§

^©Институт радиотехники и электроники РАН

^§ ЗАО «Центр ВОСПИ»

Получено 13 апреля 2004 г.

 

Аннотация

Рассмотрено влияние релаксации модуля упругости материала, заполняющего внутренние полости дефектов световодов, на скорость развития поверхностных микротрещин под нагрузкой и на прочностные характеристики волокон. Показано, что процессы релаксации существенно ухудшают прочность и долговечность световодов.

 

Проблемы прочности и долговечности волоконно-оптических световодов интенсивно исследуются многими авторами на протяжении последних 30 лет. Однако до сих пор не разработана физическая модель, объясняющая все известные из экспериментов особенности поведения волокон при различных условиях испытаний и эксплуатации. Более того, многие явления, оказывающие значительное влияние на прочность и долговечность световодов, вообще выпали из поля зрения исследователей, например, процесс релаксации упругих характеристик материалов покрытий. Покажем, что релаксация оказывает существенное влияние на скорость развития под нагрузкой поверхностных микротрещин-концентраторов механических напряжений и, как правило, снижает прочностные характеристики световодов.

При расчетах долговечности или динамических разрушающих нагрузок волоконно-оптических световодов действующее растягивающее напряжение  на первой неразорванной межатомной связи в вершинах поверхностных микротрещин обычно задают в виде [ 1, 2 ]:

 

( 1 )

 

 

где  - приложенное к образцу растягивающее напряжение, l - глубина микротрещины,  - коэффициент интенсивности напряжений,  - среднее расстояние между соседними цепочками атомов в кварцевом стекле, Y – геометрический параметр, равный  для цилиндрических стержней, и b - коэффициент концентрации напряжений, причем, как следует из ( 1 ):

 

( 2 )

 

 

Уравнения ( 1 ) и ( 2 ) получены в предположении, что радиус кривизны в вершине трещины  и остается постоянным в процессе ее роста, то есть для «острой» микротрещины и справедливы при .

В волокнах с полимерными покрытиями внутренние полости микротрещин частично или полностью заполнены материалом наносимого покрытия, скрепляющим противоположные берега дефектов. При этом часть упругой энергии, пропорциональная отношению модулей упругости заполняющего материала и кварцевого стекла 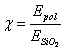, передается сквозь тело «залеченного» дефекта. Это приводит к уменьшению концентрации напряжений в вершине по сравнению с концентрацией, рассчитываемой по уравнению ( 2 ). Коэффициент b в этом случае становится равным:

 

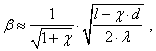
( 3 )

 

где d – глубина заполнения микротрещины, отсчитываемая от ее устья.

Можно предполагать, что из-за малых размеров внутренних полостей микротрещин и сильного влияния локальных электрических полей, ориентирующих оси молекул заполняющего материала перпендикулярно стенкам трещин, структура упаковки молекул материала внутри микротрещин близка к кристаллической. Поэтому значение модуля упругости «залечивающего» материала приближается к модулю упругости кварцевого стекла, так что .

Заполняющий микротрещину материал обладает свойством текучести под нагрузкой. Поэтому его модуль упругости изменяется во времени согласно уравнению релаксации [ 3 ]:

 

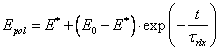
( 4 )

 

где ,  - значения модуля упругости в момент приложения нагрузки и после окончания процесса релаксации, t – время воздействия нагрузки,  - время релаксации процесса, определяемое уравнением Александрова-Гуревича [ 4 ]:

 

 

( 5 )

 

Здесь энергия активации релаксационного процесса , объем сегмента полимерной цепи , постоянная , Т- абсолютная температура среды.

Подставляя ( 5 ) и ( 4 ) в ( 3 ), получим выражение для коэффициента концентрации напряжений b с учетом релаксации модуля упругости материала, заполняющего микротрещины:

 

 

( 6 )

 

где  - коэффициент заполнения микротрещины «залечивающим» материалом.

Из уравнений ( 5 ) и ( 6 ) следует, что коэффициент b в «залеченных» микротрещинах зависит не только от глубины дефектов l, но и от величины прикладываемой растягивающей нагрузки. При больших  время релаксации  мало (), модуль упругости  уменьшается до минимального значения  за время порядка единиц секунд, коэффициент b возрастает до значения, определяемого линейными размерами дефекта, и трещина развивается с повышенной скоростью. При малых  время  большое (), и трещина растет при пониженных значениях b, то есть с меньшей скоростью. Этот эффект не учитывается исследователями, что приводит к существенным ошибкам, например, при расчетах долговечности световодов.

Покажем, что релаксация модуля упругости материала, заполняющего внутренние полости дефектов, приводит к увеличению скорости роста микротрещин в световодах с полимерными покрытиями по сравнению со скоростью развития дефектов в непокрытых волокнах при одинаковых начальных значениях коэффициента концентрации напряжений в вершинах и одинаковых скоростях нагружения .

Как известно, во влажной атмосфере скорость роста поверхностных микротрещин под нагрузкой определяется скоростью химической реакции гидролиза кварцевого стекла в локальных областях вблизи вершин дефектов [ 5, 6, 7 ]:

 

( 7 )

 

где  - энергия активации разрывов связей Si-O при гидролизе стекла, w - активационный объем, C – относительная влажность среды (в долях от единицы), k и h – постоянные Больцмана и Планка, e – близкий к единице трансмиссионный коэффициент. Обработка результатов измерений скоростей роста микротрещин в массивных образцах стекла [ 6, 8 ], дала значения энергии активации и активационного объема равные  и  при температуре среды . С ростом температуры  и w  уменьшаются. Интегрируя ( 7 ) с учетом ( 2 ) при , получаем выражение для долговечности непокрытых оболочками световодов:

 

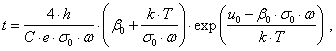
( 8 )

 

где  - начальное значение коэффициента концентрации напряжений в вершине микротрещины. Это уравнение с удовлетворительной точностью описывает результаты измерений долговечности непокрытых кварцевых волокон и массивных образцов из кварцевого стекла, приведенные, например, в работах [ 7, 9, 10 ].

При испытаниях волокон на разрывных машинах напряжение  изменяется по закону , и уравнение ( 7 ) аналитически не интегрируется. Проведено численное моделирование процесса этих испытаний, основанное на интегрировании выражения ( 7 ) для скорости роста микротрещин, которое позволило построить полиномиальные представления для разрывных нагрузок  как функции параметров ,  и . Обработка экспериментальных данных методом наименьших квадратов с использованием найденного представления для функции  позволяет находить значения ,  и получать аппроксимирующие уравнения для зависимости  от , которые обычно используются для определения параметра усталости n. (Разработанные методы расчетов будут опубликованы). Для волокон с , то есть для непокрытых световодов эта зависимость имеет вид (, ):

( 9 )

 

 

где  в МПа и в . Сравнивая ( 9 ) с известной зависимостью разрывной нагрузки от , полученной при представлении скорости роста дефекта степенной функцией [ 10 ]:

 

( 10 )

 

получим выражения для параметра усталости n и коэффициента В:

 

( 11 )

 

 

( 12 )

 

Начальное значение инертной прочности  определяется как значение напряжения , при котором показатель экспоненты в ( 7 ) обращается в нуль, поэтому:

 

( 13 )

 

Из ( 11 ) видно, что параметр n зависит от значения , то есть от начальной глубины микротрещины, и увеличивается с увеличением последней. Коэффициент В уменьшается с ростом . В непокрытых волокнах значения параметра n, рассчитанные по ( 11 ), равны 23,3 при  и 35,2 при , и совпадают по величине с типичными экспериментальными значениями, измеряемыми в массивных образцах кварцевого стекла [ 8 ].

Была проведена обработка приведенных в [ 11 ] результатов динамических испытаний покрытых оболочками волокон. Методом наименьших квадратов с использованием найденного представления для функции  определены значения энергии активации , и коэффициентов . Измеренные и расчетные значения , n и  приведены в столбцах 1 ¸ 5 таблицы 1.

Таблица 1.

Полученное при  уравнение для зависимости  от  имеет вид (, ):

 

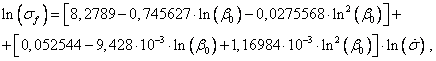
( 14 )

 

и отличается от ( 9 ) лишь значениями числовых коэффициентов. В столбце 3 таблицы 2 приведены рассчитанные по ( 14 ) значения  для волокна с начальной инертной прочностью , то есть при . Как видно, расчетные значения  хорошо согласуются с экспериментальными, приведенными в столбце 2.

Таблица 2.

Некоторое отличие расчетных значений инертной прочности от экспериментальных, приведенных в столбцах 2 и 1 таблицы 1, по-видимому, объясняются ошибками при считывании данных с графиков из статьи [ 11 ]. Значения n, вычисленные по формулам аналогичным ( 11 ), но с коэффициентами, взятыми из уравнения ( 14 ), близки к приводимым авторами значениям. Видно, что для покрытых волокон параметр n растет с ростом .

Из сказанного выше следует, что зависимость скорости роста микротрещин от нагрузки в покрытых волокнах хорошо аппроксимируется экспоненциальным уравнением ( 7 ), и процесс разрушения характеризуется энергией активации . Меньшее значение энергии активации означает, что скорость развития микротрещин под нагрузкой в покрытых световодах больше, чем в непокрытых волокнах при одинаковых начальных значениях  и скоростях нагружения . Значит, в покрытых волокнах существуют дополнительные механизмы, увеличивающие скорость роста трещин. К таким механизмам можно отнести разрушение под нагрузкой заполняющего микротрещины материала и релаксацию модуля упругости этого материала, о которой говорилось выше. Если бы процессом, определяющим энергию активации , являлось только разрушение полимерных связей, то такое же значение энергии активации должно было бы проявляться и при статических испытаниях волокон. Однако, результатам статических испытаний покрытых волокон, полученным, например, в работе [ 12 ], соответствует энергия активации , а не  как при динамических испытаниях. Такое несовпадение значений энергий активации возникает, когда начальные значения коэффициентов концентрации напряжений  в вершинах микротрещин монотонно возрастают при увеличении растягивающих напряжений при статических испытаниях или при уменьшении скоростей нагружения  при динамических испытаниях. Причиной таких изменений  может быть релаксация модуля упругости материала, заполняющего микротрещины, о чем говорилось в начале статьи. При малых скоростях  релаксация проходит более глубоко, что увеличивает начальные значения коэффициентов  и приводит к более быстрому росту микротрещин при этих скоростях. При этом скорость роста трещин описывается ( 7 ) с учетом уравнения ( 6 ).

Проявление релаксации модуля упругости материала, заполняющего микротрещины, можно проиллюстрировать следующим образом. Используя уравнение ( 9 ) для непокрытых волокон и приведенные в таблице 2 экспериментальные результаты для , можно рассчитать значения  при различных скоростях нагружения в предположении, что . Эти значения приведены в столбце 4 таблицы 2. Видно, что рассчитанные значения  уменьшаются с ростом . Наблюдаемое поведение  типично для релаксационных процессов. К сожалению, пока неизвестны параметры релаксационных процессов модуля упругости заполняющего материала, что затрудняет прямое интегрирование уравнения ( 7 ) с учетом выражения ( 6 ). Однако, некоторые оценки можно выполнить. Оценим, прежде всего, вклад релаксации упругих свойств заполняющего микротрещины материала в снижение прочности световодов. В соответствии с уравнением ( 13 ) при инертной прочности  и  коэффициент . Значение , рассчитанное с помощью уравнения ( 9 ) по экспериментальной разрывной нагрузке  при  [ 11 ], оказалось равным , что хорошо согласуется с приведенным выше значением. Можно предположить, что при столь высокой скорости нагружения релаксационные процессы не проявляются, так что найденное значение  определяется размерами дефекта. В отсутствии релаксации это значение  должно сохраняться при любых скоростях нагружения. В таком случае рассчитанные по уравнению( 9 ) разрывные нагрузки будут такими, как указано в столбце 5 таблицы 2. Из сравнения этих данных с экспериментальными видно, что релаксация значительно снижает прочность световодов.

Таким образом:

·        материал наносимого первичного покрытия частично или полностью заполняет поверхностные микротрещины, образующиеся при вытяжке световодов, и после полимеризации «залечивает» их. Это приводит  к снижению концентрации напряжений в вершинах дефектов и к повышению прочности световодов по сравнению с прочностью непокрытых волокон;

·        с другой стороны, текучесть материала, заполняющего микротрещины, приводит к постепенному уменьшению его модуля упругости при воздействии нагрузки и некоторому росту концентрации напряжений в вершинах дефектов. Это значительно ухудшает прочностные характеристики световодов, особенно при малых скоростях нагружения, по сравнению с характеристиками в отсутствие релаксации напряжений. Вызванное релаксацией уменьшение прочности может достигать 1 ¸ 1,5 ГПа;

·        с целью устранения релаксационных эффектов для первичных покрытий следует использовать материалы, имеющие меньшую текучесть под нагрузкой, например, полимеры с пространственной сшивкой молекул;

·        полученные уравнения ( 9 ) и ( 14 ), аппроксимирующие зависимости  от  для покрытых и не покрытых оболочками волокон, позволяют проводить сравнительный анализ релаксационных свойств материалов покрытий и значительно упрощают обработку экспериментальных данных, в частности, позволяют находить значения параметров В и n по задаваемым характеристикам микротрещин.

 

ЛИТЕРАТУРА

 

1.      Л.И. Седов: «Механика сплошной среды», т. 2., ((2.11), 530), М., «Наука», 1973 г., 584 стр.

2.      Г.М. Бартенев: «Прочность и механизм разрушения полимеров», ((4.14), 77 стр.), М. «Химия», 1984 г., 280 стр.

3.      В.Г. Зубчанинов: «Основы теории упругости и пластичности», «Высшая школа», 1990 г., ((13.9), стр. 293), 368 стр.

4.      В.Н. Кулезнев, В.А. Шершнев: «Химия и физика полимеров», М., «Высшая школа», 1988 г., ((10.2), стр. 150), 312 стр.

5.      Глесстон С., Лейдлер К., Эйринг Г., «Теория абсолютных скоростей реакций», Москва, Гос. изд-во иностр. лит., 1948.

6.      S.M. Wiederhorn: “Influence of water vapor on crack propagation in soda-lime glass”, J. Am. Ceram. Soc., 1967, v. 50, № 7-8, p.p. 407-414.

7.      В.А. Берштейн: «Механо-гидролитические процессы и прочность твердых тел», Л., «Наука», 1987 г., (стр. 50-57), 315 стр.

8.      Hibino J., Sakagushi S., Tajima Y., “Crack growth in silica glass under dynamic loading”, J. Am. Ceram. Soc., 1984, v. 67, № 1, p.p.64-68.

9.      B.A. Proctor, I. Whitney and J.W. Johnson: "The strength of fused silica", Proc. Roy. Soc., ser. A, v. 297, p.p. 534-542, 1967.

10.  Семенов С.Л., «Надежность, прочность, старение и деградация волоконных световодов», Волоконно-оптические технологии, материалы и устройства, Сборник трудов Учебно-научного центра волоконно-оптических материалов и устройств, Москва, 2000, № 3, стр. 47-63.

11.  Sergei.L. Semjonov, G.Scott Glaeseman, Donald A. Clark, Mikhail M. Bubnov: "Fatigue behavior of silica fibers with different defects", SPIE vol. 4215, p.p.28-35, 2001.

12.  Enrique Cuellar, Michael T. Kennedy, Daniel R. Roberts, John E. Ritter, Jr.: "Accelerated static fatigue behavior of optical glass fibers", SPIE, vol. 1973, p.p. 138-148, (1993).

 

 

Краткие сведения об авторах:

 

Дяченко Алексей Архипович, 1936 г., кандидат технических наук, ведущий научный сотрудник ИРЭ.

125009, Москва, Моховая ул., д. 11, ИРЭ РАН, тел. 203-48-36; 125445, Москва, Валдайский проезд, д. 15, кв. 61.

 

Шушпанов Олег Ефимович, 1939 г., доктор физико-математических наук, профессор, зав. лабораторией ИРЭ РАН.

125009, Москва, Моховая ул., д. 11, ИРЭ РАН, тел. 203-48-36; 125171, Москва, Ленинградское шоссе, д. 15, кв. 188, тел. 150-00-03. E-mail: oesh@cplire.ru

 

Прокофьева Лариса Петровна, 1938 г., кандидат технических наук, профессор, главный научный сотрудник ЗАО «Центр ВОСПИ».

117393, Москва ул. Обручева, д. 52, ЗАО «Центр ВОСПИ», тел. 718-38-55, 117452, Москва ул. генерала Тюленева д. 1, кв. 92, тел. 339-40-00. E-mail: center-vospi@mtu-net.ru

 

Щербаков Владислав Васильевич, 1937 г., кандидат технических наук, ведущий научный сотрудник ЗАО «Центр ВОСПИ».

117393, Москва ул. Обручева, д. 52, ЗАО «Центр ВОСПИ», тел. 718-38-55, 117452, Москва ул. генерала Тюленева д. 1, кв. 92, тел. 339-40-00. E-mail: center-vospi@mtu-net.ru

 

Таблица сокращений индексов

 

 

оглавление

дискуссия