Численное исследование СВЧ волноводных элементов на основе EBG-структуры

"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 4, 2009

ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ СВЧ ВОЛНОВОДНЫХ ЭЛЕМЕНТОВ НА ОСНОВЕ EBG СТРУКТУРЫ

С.Е. Банков¹, М.Д. Дупленкова²

¹Институт радиотехники и электроники им. В.А. Котельникова РАН

²Особое конструкторское бюро МЭИ

Получена 1 апреля 2009 г.

         Методом конечных элементов анализируются элементы волноводного тракта на основе EBG структуры из плоского волновода с решеткой металлических цилиндров. Рассматриваются различные переходы с прямоугольного металлического волновода на EBG волновод, исследуются возможности улучшения согласования за счет использования индуктивной и емкостной диафрагм, а также за счет сдвига плоскости волноводного сочленения. Исследуются переходы с EBG волновода на полосковую и коаксиальную линии, а также переходы между EBG волноводами, расположенными на разных слоях. Рассмотренные устройства оптимизируются с целью повышения их показателей качества.

Ключевые слова: EBG-волновод, численное моделирование в электродинамике.

1. Постановка задачи

         Интерес к волноводным устройствам на основе EBG структур обусловлен новыми возможностями, которые они предоставляют как с точки зрения улучшения электрических характеристик устройств, так и с точки зрения повышения их технологичности. Данное направление развивается применительно к оптическому [1] и микроволновому диапазонам [2]. В микроволновом диапазоне большой интерес представляют волноводы на основе EBG структуры (EBG волноводы) выполненной в виде двумерной решетки из металлических цилиндров, размещенных внутри плоского волновода [3]. В работе [3] предложен эффективный метод теоретического и численного анализа неоднородных EBG структур – метод компенсирующих источников. В работе [4] исследована основная волна EBG волновода, а в работе [5] представлены результаты теоретического и экспериментального исследования ряда простейших элементов.

         Целью данной работы является исследование элементов на основе EBG волноводов, имеющих более сложную структуру, чем элементы, рассмотренные в [5]. К их числу относятся, имеющие большое практическое значение, переходы, связывающие EBG волноводы с другими линиями передачи: металлическим волноводом, а также полосковой и коаксиальной линиями.

         В упомянутых выше работах устройства на основе EBG волноводов имели двумерную, однослойную структуру. Новые возможности представляют трехмерные, многослойные структуры, образованные набором плоских волноводов с решетками, имеющих общие металлические экраны. Связь между слоями обеспечивается применением специальных межслойных переходов, которые также рассматриваются в данной работе.

         Устройства, о которых говорилось выше, не могут моделироваться с помощью метода компенсирующих источников, поэтому для их анализа необходимо использовать общие подходы такие, например, как метод конечных элементов. Этот метод реализован в системе HFSS [6]. Особенностью HFSS и других систем электродинамического моделирования является то, что анализируемый многополюсник не может иметь выхода в виде периодического волновода, частным видом которого является EBG волновод. Поэтому в исследуемое устройство приходится вводить дополнительные элементы в виде переходов на стандартные линии передачи, которые имеют неидеальные параметры и не позволяют непосредственно рассчитывать матрицу рассеяния устройства с выходами в виде EBG волноводов. Для извлечения информации об исследуемом устройстве необходимо использовать дополнительную обработку результатов численных расчетов с целью исключения влияния указанных переходов. Способы обработки численных результатов рассматриваются в данной работе.

2. Переходы EBG волновод – металлический волновод

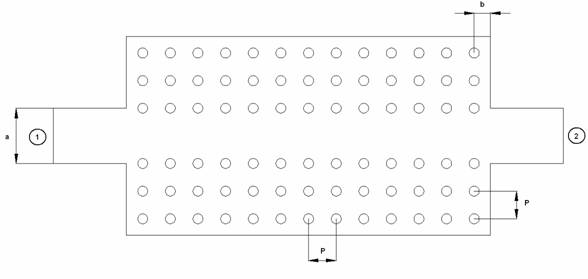
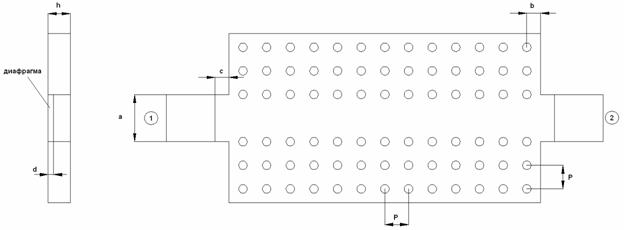
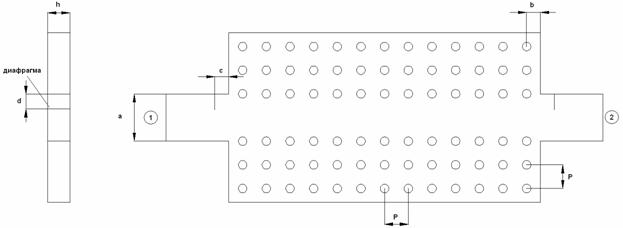
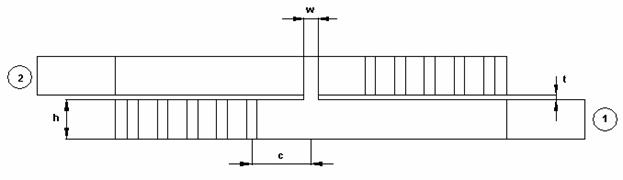
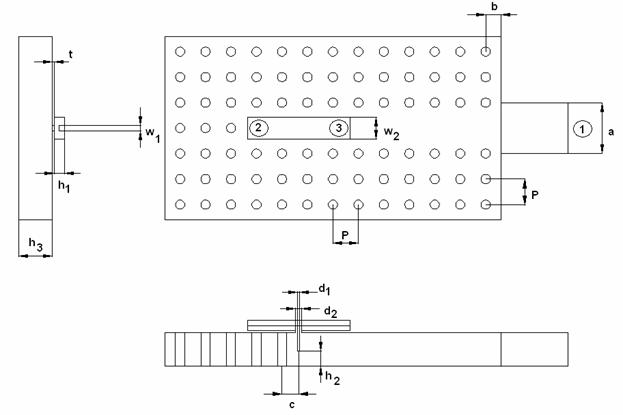
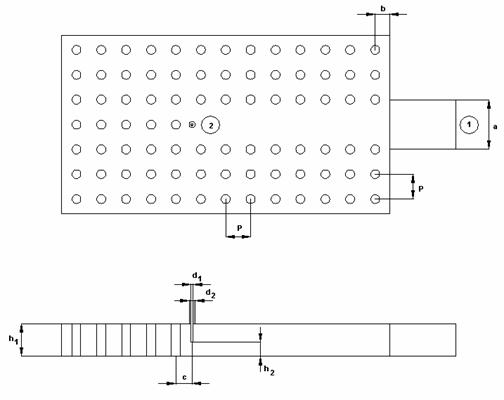
         Структура модели, использованной для численного анализа, показана на рис. 1.

Рис. 1. Модель для исследования перехода волновод – EBG волновод

Вообще говоря, нас интересует матрица рассеяния сочленения EBG волновода с металлическим волноводом. В тоже время, структура изображенная на рис. 1 включает в себя два сочленения, соединенных отрезком EBG волновода. Такое усложнение анализируемой структуры связано с отмеченной выше невозможностью установить порт в сечении периодического волновода.

         На первом этапе исследования мы изучим влияние на характеристики перехода двух параметров: ширины металлического волновода и положения плоскости сочленения волноводов двух типов, которое характеризуется расстоянием (см. рис. 1). Диаметр цилиндров, образующих периодическую структуру был принят равным 5 (здесь и далее все размеры приводятся в миллиметрах). Этот выбор определяется практическими соображениями, так как латунные цилиндры с таким диаметром являются стандартными изделиями и очень удобны для использования в диапазоне 8-12 ГГц. Следует также отметить, что их высота - совпадает с высотой стандартного металлического волновода сечением 23х10. Численные расчеты показали, что наилучшее согласование перехода достигается при равенстве высот волноводов. Поэтому использование стандартных цилиндров оказывается оптимальным с точки зрения выбора высоты EBG волновода.

         Отметим, что выбор положения плоскости сочленения двух волноводов обычно не влияет на модули элементов матрицы рассеяния их сочленения. В случае, когда один из волноводов является периодическим ситуация меняется, так как существенным фактором становится положение плоскости сочленения относительно элементов периодической решетки. Поэтому исследование влияния расстояния на характеристики перехода оказывается в нашем случае актуальной задачей.

         Предварительно период EBG структуры был выбран из условия максимальной близости постоянных распространения стандартного металлического волновода и EBG волновода в диапазоне частот 8-12 ГГц [5]. Обычно близость постоянных распространения обеспечивает наилучшее согласование волноводов. В последствии численные расчеты подтвердили справедливость этого предположения и период оставался неизменным и равным 12.5.

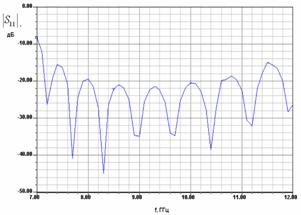
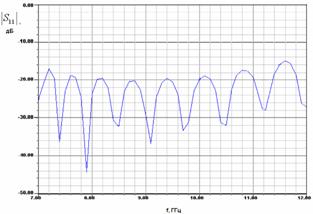
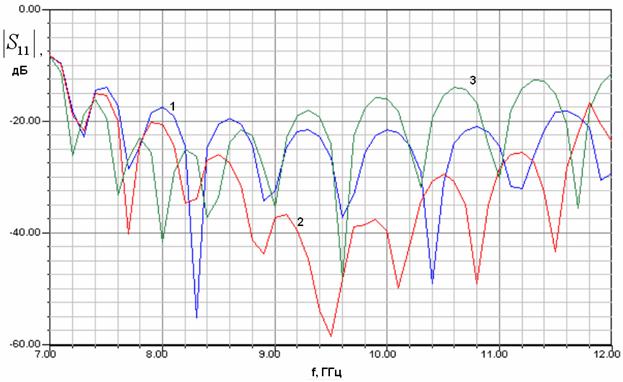
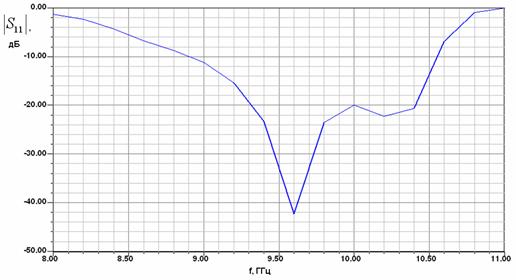
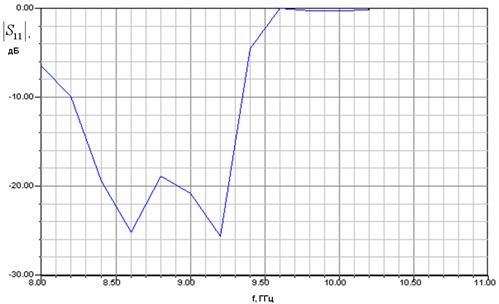
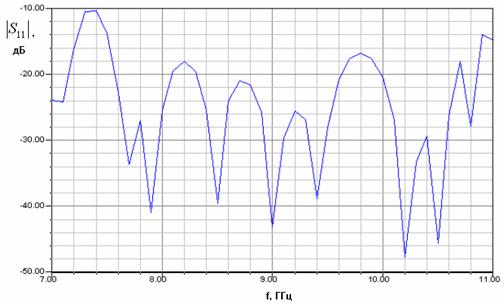
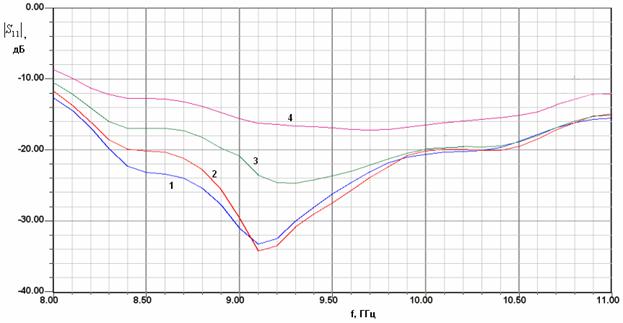
         На рис. 2 а-г показаны графики частотной зависимости модуля коэффициента отражения модели (см. рис. 1) с двумя переходами, соответствующие разным значениям ширины металлического волновода . Расстояние равно половине периода . Таким образом, длина EBG волновода, соединяющего переходы кратна целому числу периодов . Параметр был принят равным тринадцати.

                                 а                                                           б

                                 в                                                           г

Рис. 2. Частотные характеристики модели для исследования перехода волновод – EBG волновод

Кривые на рис. 2 носят осциллирующий характер типичный для двух четырехполюсников, соединенных волноводом достаточно большой длины. Перед нами стоит задача определения по матрице рассеяния численной модели матрицу рассеяния одного перехода . Изложим эту процедуру подробно. Отметим, что с небольшими изменениями она может использоваться для других устройств, рассмотренных в работе.

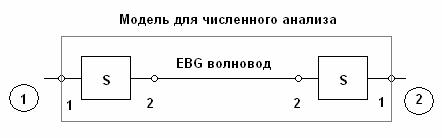
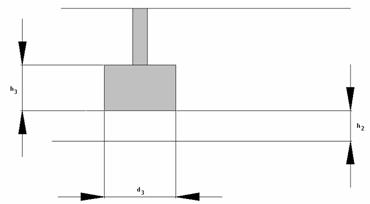
Для дальнейшего анализа нам будет полезна эквивалентная схема модели, показанная на рис. 3.

Рис. 3. Эквивалентная схема модели перехода волновод – EBG волновод

Она состоит из двух переходов, условно обозначенных прямоугольниками, и отрезка EBG волновода. Элементы матрицы рассеяния модели и можно выразить следующим образом [7]:

,                                           (1)

,

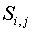
где   - элементы неизвестной матрицы рассеяния перехода, - постоянная распространения EBG волновода, а - его длина. Формулы в (1) записаны в предположении о взаимности переходов. Для достаточно хорошо согласованных переходов, которым мы относим переходы с коэффициентами отражения по модулю меньшими 0.1 знаменатель в формулах (1) мало отличается от единицы. В этом случае соотношения (1) можно записать в простой форме:

,                                                 (2)

.

Дальнейшее упрощение формул (2) связано с тем, что коэффициент передачи хорошо согласованного перехода отличается по модулю от единицы во втором порядке малости. Поэтому можно приближенно записать соотношение:

,                                                                                     (3)

где - фаза коэффициента передачи. Отметим, что фазы элементов матрицы рассеяния перехода в предположении об отсутствии у него тепловых потерь удовлетворяют следующему равенству [7]:

         ,                                                                   (4)

где - фазы коэффициентов отражения . Параметры у четырехполюсника без потерь равны по модулю:

         .                                                                                    (5)

         Считаем, что постоянная распространения EBG волновода известна. В работе [4] показано, что она с большой точностью может быть определена по методу компенсирующих источников.

         С учетом соотношений (3)-(5) для модуля коэффициента отражения модели можно записать соотношение:

         .                                                                    (6)

         Из формулы (6) видно, что модуль обращается в нуль при выполнении равенства:

         , ,                                                   (7)

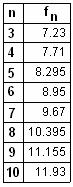
где - частоты, на которых обращается в нуль. Их можно определить из результатов численных расчетов. Частоты для волновода с приведены в табл. 1 в гигагерцах. При записи возникает проблема идентификации индекса , которую мы обсудим позднее.

         Наличие двух массивов данных и позволяет методами теории аппроксимации построить непрерывную функцию . Нами использовалась кубическая сплайн аппроксимация. Применение такого подхода оправданно только для функций, которые медленно меняются на интервалах между частотами . Это условие всегда может быть удовлетворено за счет увеличения длины EBG волновода.

         Следующий этап – определение фазы . Ее можно найти из второго уравнения (2):

         ,                                                                          (8)

где - фаза коэффициента передачи . Фазу находим из уравнения (4).

         Мы видим, что при использовании соотношения (4) возникает проблема выбора знака перед слагаемым , а в случае формулы (7) индекса . Для решения этих проблем зададимся интервалом определения фаз :

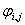
         .                                                                                (9)

         Также потребуем, чтобы фазы правой и левой частей первого уравнения (2) совпадали друг с другом. Из этих двух требований удается однозначно найти значения индекса и определить знак в (4). Окончательные значения приведены в табл. 1.

Таблица 1

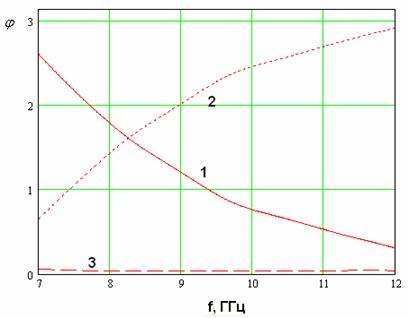
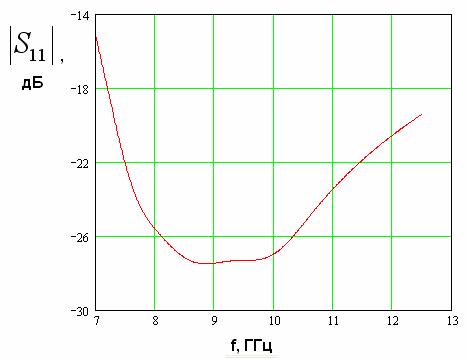
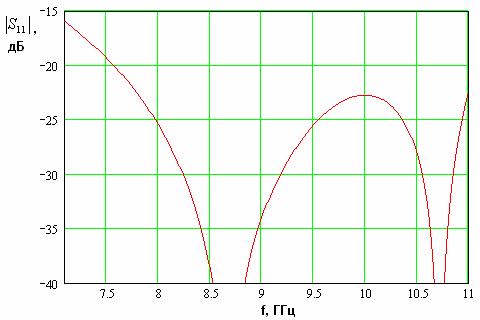
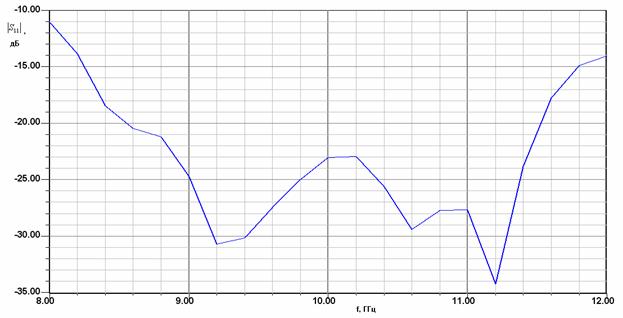
         После того как все фазы найдены, не составляет труда найти модуль коэффициента отражения из первого уравнения (2). Результаты для частотных характеристик элементов матрицы рассеяния перехода для случая показаны на рис. 4,5. На рис. 4 представлена зависимость фазы от частоты. Кривые 1-3 соответствуют , и . На рис. 5 показана зависимость модуля коэффициента отражения перехода, выраженного в децибелах, от частоты.

Рис. 4. Зависимости фаз элементов матрицы рассеяния перехода волновод – EBG волновод от частоты

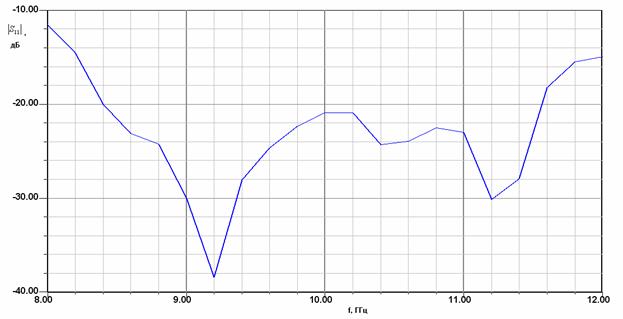
Рис. 5. Зависимость модуля коэффициента отражения перехода волновод – EBG волновод от частоты

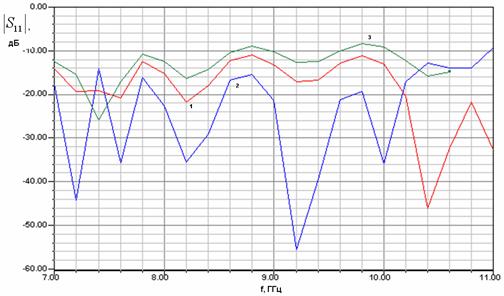
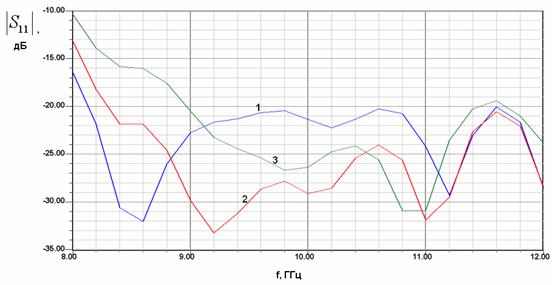
         Следующий этап исследование перехода: смещение плоскости сочленения волноводов. На рис. 6 показана частотная зависимость модуля коэффициента отражения перехода. Кривые 1-3 соответствуют , . Из рис. 6 видно, что лучшее согласование достигается, когда расстояние от центра крайнего цилиндра до плоскости сочленения равно 4.25, то есть на два миллиметра меньше половины периода EBG структуры. Графики на рис. 6 получены после обработки численных данных в соответствии с методикой описанной выше. Сдвиг плоскости сочленения позволил расширить полосу согласования перехода. Если для исходного положения (кривая 1) полоса согласования по уровню –25 дБ составляла 2.7 ГГц, то после смещения она увеличилась до 3.7 ГГц.

Рис. 6. Зависимость модуля коэффициента отражения перехода волновод – EBG волновод от частоты при разных положениях плоскости сочленения



Следующий этап исследования перехода: анализ возможностей его согласования с помощью реактивных диафрагм. Модель, использованная при численном решении в случае емкостной диафрагмы, показана на рис. 7, а на рис. 8 в случае индуктивной диафрагмы. При проведении оптимизации устройства мы предполагали, что плоскость сочленения не обязательно должна совпадать с плоскостью включения диафрагмы.

Рис. 7. Модель для исследования перехода волновод – EBG волновод с емкостной диафрагмой

Рис. 8. Модель для исследования перехода волновод – EBG волновод с индуктивной диафрагмой

         Исследование переходов данного типа показало, что лучшие результаты получаются с емкостными диафрагмами, когда они расположены в плоскости сочленения волноводов, то есть при . На рис. 9 показаны зависимости от частоты модуля коэффициента отражения модели при разных значениях размера диафрагмы , которым соответствуют кривые 1-3. Параметр при этом был равен 4.25. Ширина металлического волновода равна 23, что соответствуют размеру стандартного волновода. Период решетки и диаметр цилиндров такие же, как в случае перехода без диафрагм.

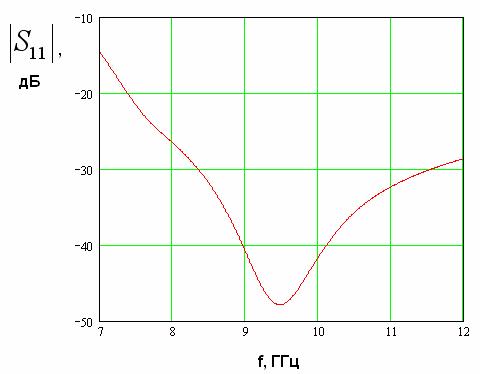
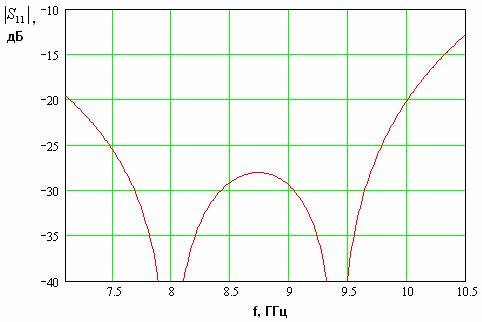
         После обработки численных данных были получены частотные зависимости элементов матрицы рассеяния перехода с емкостной диафрагмой. На рис. 10 представлена кривая частотной зависимости модуля коэффициента отражения для оптимального значения . Видно, что использование диафрагмы дополнительно увеличивает полосу согласования перехода по уровню – 25 дБ, которая теперь превышает значение 4.5 ГГц.

Рис. 9. Зависимости модуля коэффициента отражения модели перехода волновод – EBG волновод с емкостной диафрагмой от частоты при разных размерах диафрагмы

Рис. 10. Зависимость модуля коэффициента отражения перехода волновод – EBG волновод с емкостной диафрагмой от частоты

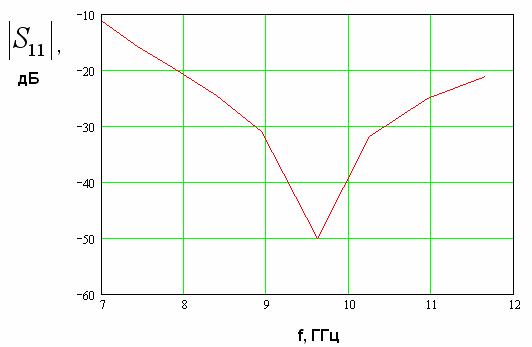
         Использование индуктивной диафрагмы дает существенно более узкую полосу согласования. Пример частной характеристики перехода в этом случае приведен на рис. 11. Зависимость модуля коэффициента отражения от частоты получена для , , . Сужение полосы согласования связано с тем, что индуктивную диафрагму приходится размещать на значительном расстоянии от плоскости сочленения волноводов, что всегда усиливает частотную зависимость параметров устройства.

Рис. 11. Зависимость модуля коэффициента отражения перехода волновод – EBG волновод с индуктивной диафрагмой от частоты

3. Межслойные переходы

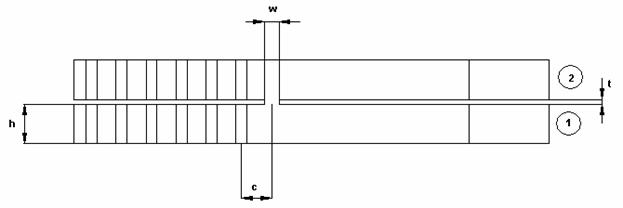
         Были рассмотрены два типа межслойных переходов: сонаправленный и противонаправленный. Конструкция модели, использованной для численного исследования сонаправленного перехода показана на рис. 12. Видно, что волны в плечах 1 и 2 при условии их согласования распространяются в одинаковых направлениях, что служит основанием для классификации перехода как сонаправленного. Ниже будет показано, что в противонаправленном переходе волны в разных плечах движутся в противоположных направлениях.

Рис. 12. Модель сонаправленного межслойного перехода

         Рассматриваемый межслойный переход образован двумя полубесконечными EBG волноводами, расположенными на разных уровнях. Они разделены общим металлическим экраном толщиной . Связь волноводов обеспечивается за счет щели связи, которая имеет ширину и длину . Нижний волновод «закорочен» слева цилиндрами EBG структуры, а верхний волновод «закорочен» справа. По этой причине в конструкции перехода присутствуют два короткозамкнутых шлейфа длиной .

         В функционировании межслойных переходов обоих типов можно выделить два режима, которые существенно отличаются друг от друга. Смена режима работы зависит от высоты плоского волновода , который образуется в области щели связи. В этом волноводе кроме основной Т-волны возбуждаются также высшие типы волн. Первый высший тип волны имеет критическое значение высоты равное половине длине волны в среде, которая заполняет волновод. Если параметр превышает критическое значение, то рассматриваемая волна становится распространяющейся, в противном случае она является нераспространяющейся, запредельной. Режим распространения волны определяет режимы функционирования перехода, которые можно назвать режимами распространения и запирания. По аналогии с работой [8], в которой рассматривался межслойный переход квазиоптического типа.

         Обработка численных результатов для межслойных переходов имеет ряд особенностей. Они связаны с тем, что теперь мы можем считать, что матрица рассеяния перехода металлический волновод – EBG волновод известна. Выразим в приближении малых коэффициентов отражения коэффициенты отражения и прохождения модели через известные элементы матрицы рассеяния перехода волновод – волновод и неизвестные S – параметры межслойного перехода:

         ,

,                                                     (10)

где - расстояние от входа модели до отсчетной плоскости межслойного перехода, которая расположена в центре щели связи. Индекс п в (10) означает, что данный параметр относится к переходу волновод – волновод. Параметры рассеяния межслойного перехода даны без индексов. Выражения (10) получены при условии взаимности и отсутствия тепловых потерь в модели. Переменные знаки появились в (10) из соотношения, связывающего фазы четырехполюсника без потерь:

         .                                                                               (11)

Из второго уравнения (10) сразу можно найти фазу коэффициента прохождения через межслойный переход :

.                                                            (12)

Далее из первого уравнения (10) не составляет труда определить знак в формуле (10) и модуль коэффициента отражения межслойного перехода:

.                                 (13)

         При проведении численных расчетов мы использовали два значения высоты плоского волновода равные 5 и 10. При реализуется режим запирания, а при режим распространения. Отметим, что в режиме распространения переходы имеют существенно более узкие полосы рабочих частот, в которых они хорошо согласованы. На рис. 13, 14 показаны типичные зависимости модуля коэффициента отражения от частоты модели сонаправленного перехода в режиме распространения. Кривые получены для следующих параметров: , , . Графики на рис. 13 соответствуют , , а на рис. 14 , . Объяснение относительно узкой полосы согласования перехода связано с необходимостью использования весьма длинных короткозамкнутых шлейфов.

Рис. 13. Частотная характеристика модели сонаправленного межслойного перехода в режиме распространения при настройке на частоту 10 ГГц

Рис. 14. Частотная характеристика модели сонаправленного межслойного перехода в режиме распространения при настройке на частоту 8.8 ГГц

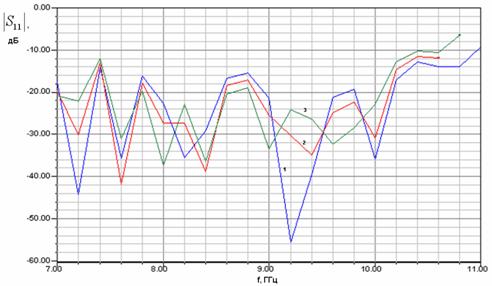
         На рис. 15,16 показана частотная зависимость модуля коэффициента отражения модели сонаправленного перехода в режиме запирания (). Кривые 1-3 на рис. 15 получены для w=1, 2, 3, L_s=27, c=6.5, а кривые 1-3 на рис. 16 для w=2, L_s=27,28,29, c=6.5. Лучшее согласование достигается при w=2, L_s=29. Оптимальным параметрам соответствует рис. 17, на котором показан модуль коэффициента сонаправленного перехода как функция частоты. Она была получена в результате обработки численных данных. Видно, что переход согласован по уровню –20 дБ в полосе около 3 ГГц.

Рис. 15. Частотная характеристика модели сонаправленного межслойного перехода в режиме запирания при разной ширине щели

Рис. 16. Частотная характеристика модели сонаправленного межслойного перехода в режиме запирания при разной длине щели

Рис. 17. Зависимость модуля коэффициента отражения сонаправленного межслойного перехода в режиме запирания от частоты

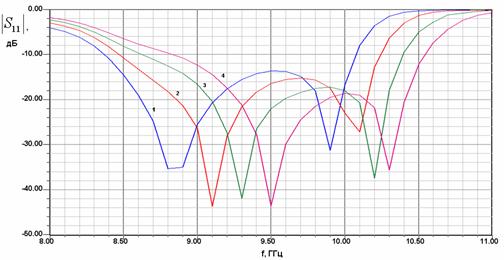
         Модель для численного исследования противонаправленного перехода изображена на рис. 18. На рис. 19 представлены графики зависимости модуля коэффициента отражения от частоты перехода в режиме распространения (). Кривые 1-4 соответствуют c=25,26,27,28. Остальные параметры имели следующие значения: L_s=19, t=1,w=7.

Рис. 18. Модель противонаправленного межслойного перехода

         Кривая на рис. 20 соответствует модели противонаправленного перехода в режиме запирания () с оптимальными геометрическими параметрами: w=3, L_s=24, c=4, t=1. Этим же параметрам соответствует рис. 21, на котором показан коэффициент отражения перехода после обработки данных. Из рис. 17,21 видно, что в режиме запирания переходы обоих типов имеют близкие частотные характеристики с двумя глубокими провалами. Их наличие обеспечивает относительно широкую полосу согласования.

Рис. 19. Частотная характеристика модели противонаправленного межслойного перехода в режиме распространения при разном расстоянии от щели до металлических цилиндров

Рис. 20. Частотная характеристика модели противонаправленного межслойного перехода в режиме запирания

Рис. 21. Зависимость модуля коэффициента отражения противонаправленного межслойного перехода в режиме запирания от частоты

4. Переход EBG волновод – полосковая линия

         Структура модели для численных исследований волноводно – полоскового перехода показана на рис. 22. Полосковая линия представляет собой металлическую полоску шириной помещенную между двумя горизонтальными экранами, расположенными на расстоянии друг от друга. Для численного анализа удобно также ввести вертикальные экраны, которые вместе с горизонтальными экранами образуют замкнутый объем. Таким образом, вместо полосковой линии, которая обычно содержит только горизонтальные экраны, мы получаем коаксиальную линию с плоским проводником. Однако, это отличие несущественно, так как, выбирая расстояние между вертикальными экранами достаточно большим, можно исключить их влияние на электрические характеристики полосковой линии. На практике достаточно, чтобы выполнялось следующее неравенство:

         .                                                                              (10)

Рис. 22. Модель волноводно – полоскового перехода

Волноводно – полосковый переход содержит короткозамкнутый отрезок EBG волновода, который связан с полосковой линией через зонд, выполненный в виде металлического цилиндра диаметром . В верхнем экране EBG имеется отверстие диаметром . Через это отверстие проходит зонд, имеющий электрический контакт с полосковым проводником. Глубина погружения зонда в EBG волновод - . Расстояние от центра зонда до центра ближайшего короткозамыкающего цилиндра - . Модель для численного анализа содержит три порта. Порт 1 волноводный, а порты 2 и 3 полосковые.

         Идентификация параметров волноводно – полоскового и волноводно – коаксиального переходов осуществляется элементарно и мы не будем останавливаться на ней подробно.

         На рис. 23 показаны графики частотной зависимости модуля коэффициента отражения модели, полученные при следующих параметрах: c=4.25, d₁=1, d₂=3, t=0.5, w₁=2, h₁=4, h₃=10, w₂=10, P=12.5, D=5. Параметры полосковой линии выбраны таким образом, что ее волновое сопротивление равно 100 Ом (см. [9]). Кривые 1-3 соответствуют разной глубине погружения зонда h₂=3.5,3.75,4. Из рис. 23 видно, что оптимальное значение параметра h₂, обеспечивающее максимальную полосу согласования перехода равно 3.5. Частотная характеристика самого перехода для оптимальной глубины погружения, полученная путем обработки численных результатов показана на рис. 24.

Рис. 23. Частотная характеристика модели волноводно – полоскового перехода при разной глубине погружения зонда

Рис. 24. Зависимость модуля коэффициента отражения волноводно – полоскового перехода от частоты

         Обращает на себя внимание весьма широкая полоса согласования устройства, определенная по уровню – 20 дБ. Она превышает величину 4 ГГц. Характерно, что внутри полосы согласования незначительно меньше контрольного уровня в – 20 дБ. Ниже уровня – 25 дБ он опускается в существенно более узкой полосе частот около 0.5 ГГц.

5. Переход EBG волновод – коаксиальная линия

         В ходе исследований были рассмотрены разные конструкции волноводно – коаксиальных переходов. Первым из них был зондовый переход, показанный на рис. 25. Он имеет структуру типичную для устройств такого класса. Модель для численных расчетов имеет два порта: порт 1 волноводный, а порт 2 – коаксиальный. Внешний и внутренний диаметры коаксиальной линии и были выбраны равными 3.5 и 1.0. Пространство коаксиальными проводниками заполнено фторопластом (). При этих условиях линия имеет характеристическое сопротивление равное 50 Ом.

Рис. 25. Модель зондового коаксиально – волноводного перехода

         Настройка перехода заключается в выборе глубины погружения центрального проводника линии в волновод, которая описывается параметром и расстоянием от центра проводника до центра ближайшего цилиндра, закорачивающего EBG волновод - . Процесс настройки показан на рис. 26, на котором представлена частотная зависимость модуля коэффициента отражения модели. Кривые 1-3 соответствуют разным значениям параметра . Расстояние равно 7.3. Высота плоского волновода принята равной 10. Период решетки и диаметры образующих ее цилиндров, как и раньше равны 12.5 и 5 соответственно.

Рис. 26. Частотная характеристика модели коаксиально – волноводного перехода при разной глубине погружения зонда

Рис. 27. Зонд с участком с увеличенным диаметром

         Наилучшему согласованию соответствует кривая 1 на рис. 26. Полоса согласования по уровню – 20 дБ не превышает 1 ГГц. Расширение полосы согласования можно добиться, изменяя форму части центрального проводника, погруженной в волновод, например, выполняя ее в форме цилиндра с диаметром большим , как показано на рис. 27.

         Типичная зависимость модуля коэффициента отражения модели перехода с расширенным центральным проводником от частоты показана на рис. 28. Расчеты проводились при , , . Кривые 1-4 соответствуют следующим значениям параметра =3.8, 3.9, 4.0, 4.2. Видно, что полоса согласования расширилась до значений близких к 2 ГГц.

Рис. 28. Частотная характеристика модели коаксиально – волноводного перехода с зондом, имеющим участок с увеличенным диаметром при разной глубине погружения зонда

         Следующий вариант волноводно – коаксиального перехода показан на рис. 29. Его отличие от рассмотренных выше в продольном расположении коаксиальной линии, которая размещается в отверстиях в цилиндрах, закорачивающих EBG волновод. Центральный проводник коаксиальной линии продолжается металлической лентой, которая вводится внутрь волновода. В конце лента соединяется с металлическим цилиндром диаметром . Таким образом, металлическая лента, цилиндр, участок стенки EBG волновода и цилиндр, закорачивающий EBG волновод образуют петлю, которая связывает волновод и коаксиальную линию по магнитному полю, в отличие от рассмотренных выше зондовых структур, осуществлявших связь по электрическому полю.

Рис. 29. Модель продольного коаксиально – волноводного перехода

         Численные расчеты показали, что продольное размещение коаксиальной линии существенно увеличивает полосу согласования перехода. В этом можно убедиться, анализируя рис. 30, 31, на которых показаны частотные зависимости модуля коэффициента отражения модели перехода со стороны волновода. График на рис. 30 получен для следующих параметров: h₂=3.1, d₁=1, d₂=3.5, d_c=2, L₁=7.5, L₂=0.6, h₁=10. Диаметр цилиндров, образующих EBG структуру и ее период равны 5 и 12.5 соответственно. График на рис. 31 получен для тех же параметров за исключением высоты h₂, которая равна 3.2.

Рис. 30. Частотная характеристика модели продольного коаксиально – волноводного перехода при h₂=3.1

Рис. 31. Частотная характеристика модели продольного коаксиально – волноводного перехода при h₂=3.2

         Работа выполнена при поддержке Российского фонда фундаментальных исследований, грант 08-08-12200-офи.

СПИСОК ЛИТЕРАТУРЫ

1.     Mekis A., Chen J.C., Kurland I. at all // Phys. Rev. Lett. 1996. V. 77, № 18. P. 3787.

2.     Simpson J.J, Taflove A., Mix J.A., Heck H. // IEEE Microwave and Wireless components letters. 2004. V. 14. №7. P. 356.

3.     Банков С.Е. // PЭ. 2005. Т. 50. №1. С. 23.

4.     Банков С.Е. // РЭ. 2006. Т.51. №5. С. 533.

5.     Банков С.Е., Пангонис Л.И. // РЭ. 2008. Т.53. №3. С. 295.

6.     С.Е. Банков, А.А. Курушин, В.Д. Разевиг. Анализ и оптимизация трехмерных СВЧ структур с помощью HFSS // М.: Солон-Пресс. 2005.

7.     Сазонов Д.М. Антенны и устройства СВЧ. М.: Высш. школа. 1988.

8.     С.Е. Банков. // РЭ. 2004. Т.49. №6. С. 701.