ВЫВОД ВЫРАЖЕНИЯ ДЛЯ ТЕРМОДИНАМИЧЕСКОГО ПОТЕНЦИАЛА «ГРЯЗНОГО» СВЕРХПРОВОДНИКА
А. В. Семенов1, И. А. Девятов2, А. А. Корнеев1,
К. В. Смирнов1,
Г. Н. Гольцман1, А. П. Мельников1
1 Московский Педагогический Государственный Университет
2 НИИЯФ
им. Д.В. Скобелицина МГУ им. М.В. Ломоносова
Получена 16 апреля 2012 г.
Аннотация. Получена формула для термодинамического потенциала «грязного» сверхпроводника, выражающая его через квазиклассические функции Грина теории Узаделя. Результат даёт возможность единообразного описания динамических процессов и флуктуаций в устройствах сверхпроводниковой наноэлектроники.
Ключевые слова: сверхпроводниковая наноэлектроника, теория Узаделя, термодинамический потенциал.
Abstract. We derive a formula for thermodynamic potential of dirty superconductor which express it via isotropic quasiclassical Green functions of Usadel theory. Our result allows unify description of dynamic processes and fluctuations in superconducting nano-electronic devices.
Keywords: superconducting nano-electronics, Usadel theory, thermodynamic potential.
Материалы, из которых изготавливаются современные устройства сверхпроводниковой наноэлектроники, в силу особенностей тонкоплёночной технологии обычно удовлетворяют условию грязного предела – длина свободного пробега в них мала по сравнению с длиной когерентности. Поэтому для описания работы таких устройств в случаях, когда требуется привлечение микроскопической теории, обычно используется подход, основанный на справедливых для грязных сверхпроводников уравнениях Узаделя [1-3]. Важным достоинством этих уравнений является их относительная простота, позволяющая практически всегда точно решить их численно и в некоторых случаях – аналитически.
При рассмотрении флуктауционных явлений удобно, наряду с динамическими величинами – параметром порядка, сверхтоком, функциями Грина, – оперировать термодинамическими потенциалами. Однако в литературе не имеется готовых выражений для термодинамических потенциалов сверхпроводника через изотропизированые функциями Грина G и F, что препятствует последовательному использованию теории Узаделя. Настоящая работа имеет своей целью заполнить этот пробел.
Мы будем исходить из результата теории Эйленбергера, выражающего термодинамический потенциал сверхпроводника через квазиклассические функции Грина g, f, f+, векторный потенциал A и параметр порядка Δ (предполагается сферическая симметрия поверхности Ферми) [4].
, (1)
,
, (1а)
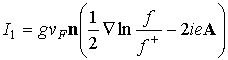, (1б)
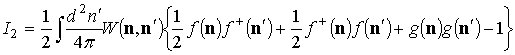. (1в)
Здесь N0 – плотность состояний на уровне Ферми, vF – скорость Ферми, W – матричный элемент упругого рассеяния, T – температура, ω – мацубаровская частота, n – единичный вектор в направлении скорости Ферми (g, f, f+ являются функциями n и ω). Даваемый этим выражением термодинамический потенциал отсчитывается от термодинамического потенциала нормального состояния.
Чтобы получить выражение для Φ через узаделевские функции Грина, нужно, как это обычно делается в диффузном пределе, разложить g, f, f+ в ряд по сферическим полиномам Лежандра, а затем выполнить усреднение по углам. При этом в членах I0, I1 достаточно ограничиться разложением до слагаемых первого порядка:
,
,
.
В силу соотношений f+(n)=f*(−n) [2], имеем F+=F*, F+=−F*.
Усреднение в члене I0 выполняется очевидно:
. (2)
Среднее по углам от члена I1 с точностью до первого порядка есть
.
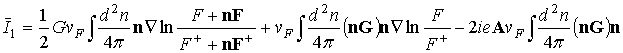Поскольку усреднение по направлениям вектора n и дифференцирование по координате не зависят друг от друга, в первом слагаемом можно сначала выполнить усреднение, а затем найти дивергенцию. При выполнении усреднения введём систему координат, положив F=e1F1.
,
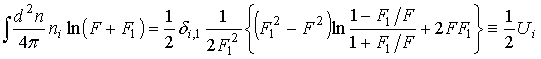Эти выражения не вполне удовлетворительны, поскольку F и F+, будучи выражены через F, F+, G и A (см. ниже формулы (6)), содержат в явном виде длину свободного пробега ℓ, а уравнению Узаделя формально соответствует предел ℓ→0. Тем самым необходимо сделать этот переход и во всех составляющих выражения для термодинамического потенциала. Это делается тривиально в случае, если F нигде не обращается в 0. Тогда отношение F1/F является малым параметром и достаточно просто разложить конструкции с логарифмом в фигурных скобках в ряд по F1/F с точностью до первых неисчезающих членов:
,
что даёт для 
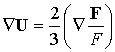. (3)
В случае, когда F в некоторой точке обращается в 0 (что реализуется,
например, для центра проскальзывания фазы при равном нулю токе), условие F1/F<<1
перестаёт выполняться в окрестности этой точки шириной порядка ℓ.
В точках, где F1=±F,
будет иметь особенности, хотя, как можно показать, и
интегрируемые. При этом ясно, что физического смысла резкие изменения (и с ней 
) на
масштабе длины порядка ℓ, несвойственном уравнению Узаделя, не
имеют. Очевидный способ регулярзовать член – сначала сгладить выражение для на масштабе длины порядка ℓ, а затем уже
произвести предельный переход ℓ→0.
Проще, однако, поступить иначе: изменить подынтегральное выражение в
формуле для термодинамического потенциала таким образом, чтобы интеграл по
объему сверхпроводника остался неизменным, а особенности в подынтегральном
выражении исчезли. Мы проведём эту процедуру для случая одномерной проволоки,
введя для удобства дополнительное предположение, что сверхпроводящее состояние
на концах проволоки однородно (окончательный результат от этого не зависит и
справедлив как для одномерного случая, так и для трёхмерного). Перепишем
интересующую нас часть члена в
виде
.
Интеграл от первого слагаемого по всей длине проволоки даст 0, поскольку на концах обращается в ноль U. Поэтому первое слагаемое можно опустить. Второе слагаемое перепишем так:
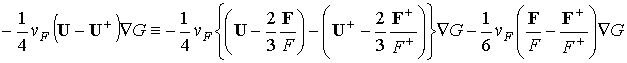
Вклад в интеграл от первого члена даёт лишь область размером порядка ℓ
вблизи нуля функции F, где отличен
от своего приближённого выражения. В пределе ℓ→0 вклад в
интеграл от первого члена исчезает, и, таким образом, для рассматриваемой части
можно использовать выражение
.
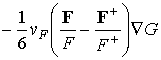При усреднении других слагаемых члена I1 подобных сложностей не возникает. Для всего члена получается
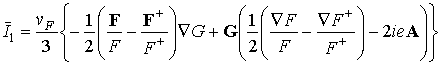. (4)
Теперь прейдём к усреднению по углам члена I2. Конструкция из функций Грина в фигурных скобках обращается в ноль как в нулевом, так и в первом порядке разложения в ряд по полиномам Лежандра, что, однако, не приводит к пренебрежимой малости члена I2 по сравнению с I0,1 благодаря наличию в I2 большого множителя W~τ−1 (частота упругого рассеяния τ−1 в грязном пределе велика по сравнению с Δ). Поэтому требуется проводить разложение до второго порядка:
,
,
.
Индексы нумеруют проекции на координатные оси, по дважды повторяющимся индексам подразумевается суммирование.
Конструкция в фигурных скобках из (1в) во втором порядке имеет вид
.
При усреднении I2 по углам учтём, что, в соответствии с определениями времён свободного пробега τ и τtr,
,
.
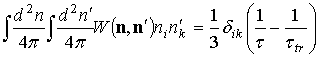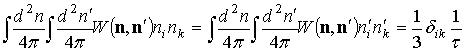Кроме того, воспользуемся тождеством
,
которое получается, если взять аналогичный интеграл от записанного во
втором порядке условия нормировки функций Грина 
:
.
В результате для 
приходим
к следующему компактному выражению
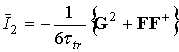. (5)
Для приведения выражения для термодинамического потенциала к окончательному виду осталось выразить входящие в (4) и (5) векторные функции Грина F, F+ и G через входящие в уравнения Узаделя F, F+, G, их градиенты и векторный потенциал:
, (6а)
, (6б)
, (6в)
После подстановки этих формул в (4) и (5) получается
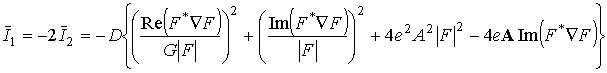, (7)
где D=vFℓ/3 – коэффициент диффузии
Таким образом, приходим к следующей формуле, выражающей термодинамический потенциал через функции Грина теории Узаделя:
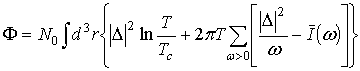, (8)
.
Формула (8) представляет собой основной результат настоящей работы.
Работа выполнена в рамках реализации ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России» на 2007—2012 гг.
1. K. D. Usadel, Phys. Rev. Lett. 25, 507 (1970).
2. W. Belzig, F. K. Wilhelm, C. Bruder, G. Schön and A. D.Zaikin, Superlattices and Microstructures, 25, 1251 (1999).
3. A. A. Golubov, M. Yu. Kupriyanov, E. Il’ichev, Rev. Mod. Phys. 76, 411 (2004).
4. G. Eilenberger, Zeitschrift fur Physik 214, 195 (1968).