Особенности восстановления искаженного оптической системой радиоизображения с помощью метода опорного изображения

 

А. Ю. Зражевский, В. А. Коротков

ИРЭ им. В.А. Котельникова РАН,  Фрязинский филиал

Получена 9 апреля 2013 г.

 

Аннотация. В работе рассмотрена возможность восстановления искаженного оптической системой радиоизображения с помощью метода опорного изображения. Показано, что эффективность метода определяется его способностью выделять спектральную область, содержащую шум произвольного происхождения.

Ключевые слова: радиовидение, миллиметровый диапазон волн, аппаратная  функция, радиотепловое изображение, восстановление изображения, опорное изображение.

Abstract. The possibility of using the reference image for the restoration of radio image, distorted by optical system, is considered.  It is shown that the efficiency of the method is determined by its ability to isolate the spectral region containing the origin of any noise.

Key words: radio-wave imaging, millimeter-wave instrument function, radiothermal image, image recovery, backup image.

 

В процессе формирования и получения (измерения) радиоизображения происходят неизбежные искажения, вызванные различными причинами. Эти причины могут быть обусловлены формирующими изображение (оптическими) системами.   Известно [1], что оптические искажения изображения определяются аппаратной функцией (АФ) приемной системы и сопровождаются изменениями в пространственном спектре изображения. Для компенсации этих изменений применяются различные методы [1,3]. Одна из основных задач, связанных с использованием этих методов, состоит в определении параметров всех шумов (помех), влияющих на приемный сигнал. Однако на практике обычно ограничиваются некими «разумными» предположениями о характере и параметрах возникающих шумов.

В данной работе применяется альтернативный метод [2,4], не требующий знания шумов влияющих на принимаемый сигнал. Этот метод основан на том, что пространственный спектр изображения имеет некоторые свойства, коренным образом отличающиеся от пространственных спектров шумов, искажающих полученное изображение.

Метод опорного изображения – МОИ [2],  основан на фильтрации спектра изображения с применением для сравнения опорного изображения. Поэтому такой подход позволяет отфильтровывать помехи вне зависимости от их параметров и источника. Следует отметить, что в этом методе помехой (шумом) считается та часть спектра, которая энергетически превосходит некий порог, заданный усредненным спектром опорного изображения.

Если известна аппаратная функция (АФ) системы h(x, y) и исходное  изображение f(x , y ), то изображение на выходе этой системы g(x,y) можно записать в виде свертки [1]:

                                               (1)

 

где D – область наблюдения, dx₁ dy₁  - элементарная площадка в точке (x₁ , y₁).

На АФ накладывается условие нормировки что обеспечивает сохранение средней яркости изображения.

Спектральные представлениям исходного изображения f(x,y), изображения, получаемого на выходе системы g(x,y), и аппаратной функции h(x, y) можно записать в виде:

                             (2)

,

,

 

В частотной области пространственный спектр G(w_x , w_y ) изображения на выходе системы выражается через спектр исходного изображения и H(w_x,w_y):

.                                                 (3)

 

Из этого следует, что если известна H(w_x, w_y), восстановленный спектр исходного изображения F (w_x , w_y ) можно получить по формуле (инверсная фильтрация):

                                                (4)

 

после чего «восстановленное» изображение f(x,y) рассчитывается по формуле обратного Фурье-преобразования:

         ,                             (5)

 

Выражение (4) показывает возможное сильное влияние малых значений H(w_x,w_y) спектра АФ.

Легко убедится, что использование (4) – так называемая инверсная фильтрация – часто приводит к печальным результатам. Восстановленное таким способом изображение не позволяет опознать находящиеся на нем объекты – Рис.6.

Выходом из этого может быть описанный в [2] метод опорного изображения (МОИ). Для применения этого метода следует выбрать опорное изображение, спектр которого имеет характеристики схожие со спектром восстанавливаемого. Для того, чтобы различия между этими спектрами не были слишком критичными, используется не сам спектр, а его усредненный согласно МОИ амплитудный спектр опорного изображения. Каждая точка этого спектра рассчитывается по следующему алгоритму. С помощью плавающего окна – спрайта, в центре которого находится рассматриваемая точка, рассчитывается средняя по спрайту амплитуда – m и среднеквадратичное отклонение – s и, наконец, находится по формуле (6) порог – n, превышение над которым амплитуды восстанавливаемого инверсной фильтрацией изображения говорит о том, что в данной точке содержится шум.

 

          n = m + a * s ,                                                                                (6)

 

где m – средняя амплитуда по спрайту спектра опорного сигнала, s – среднеквадратичное отклонение, a – варьируемый коэффициент. В дальнейшем при расчетах всюду a=4.

Сравнивая модуль спектра в данной точке (пикселе) с вычисленной в этом пикселе величиной n по МОИ определяется что находится в данной точке сигнал или шум. Если модуль спектра в данном пикселе превосходит n, то этот пиксель содержит сигнал, а иначе шум.

Если согласно МОИ в рассматриваемой точке спектра содержится сигнал, то значение в этой точке не меняется. Если по МОИ определено, что в данной точке спектра находится шум, то модуль спектра в этой точке приравнивается n, а фаза сохраняется неизменной. Что это значит?

Рассмотрим применение этого метода, используя для иллюстрации как сами изображения, так и их спектры. Спектры представим в виде десятичных логарифмов модулей, нормированных так, чтобы значения лежали в интервале 0-255, причем 255 соответствует белому цвету и большей интенсивности.

Возьмем для иллюстрации этого в качестве исходного изображения Рис 1.

 

Рис.1 Исходное изображение и его амплитудный спектр.

 

В качестве опорного изображения возьмем Рис.2.

 Рис.2. Опорное изображение и его амплитудный спектр.

 

В дальнейшем, для применения МОИ, будет использоваться не сам спектр опорного изображения, а его усредненный вариант, представленный на Рис.3.

 

Рис.3. Спектр усредненного опорного изображения согласно основной формуле (6) с использованием среднего по спрайту 4х4 и среднеквадратичного отклонения.

 

   Произведем фильтрацию изображения Рис.1 с помощью аппаратной функции Гаусса при S = 4 :

,

где S – среднеквадратичное отклонение.

Выбор такого фильтра определялся тем, что этот фильтр весьма эффективно подавляет высокие частоты за пределами полосы пропускания.

Получим Рис.4.

Рис.4. Расфокусированное изображение и его амплитудный спектр при S=4.

Далее мы запишем полученное изображение в BMP файл и считаем его. Считанное из файла изображение на глаз неотличимо от Рис.4. Однако его спектр изменится достаточно сильно – Рис.5.

 

Рис.5. Спектр расфокусированного изображения, показанного на Рис.4, после записи изображения в BMP файл и считывания из него.

 

Сравнение спектров на рис.1, 4 и 5 позволяет сделать очевидный вывод о сильном подавлении высоких пространственных частот Гауссовой фильтрацией и замене информации об изображении на высоких частотах цифровым шумом при операциях записи-чтения BMP файла.

Попытка восстановить исходное изображение с помощью метода инверсной фильтрации успеха не приносит – Рис.6.

а                                                           б

Рис.6. Результат применения метода инверсной фильтрации. Полученное изображение а и его амплитудный спектр б

 

Понятно, что применение инверсной фильтрации безуспешно именно из-за замены информации об изображении на шум на высоких частотах. Амплитуда этого шума после инверсной фильтрации будет полностью подавлять исходное изображение. Этот шум хорошо виден на спектре (см. Рис.6 ) в виде белого и светло-серого обрамления низкочастотного информативного темно-серого центрального пятна.

Применение метода опорного изображения более успешно – Рис.7.

  На Рис.7 хорошо видно, что МОИ правильно определил информативную часть спектра и нормировал остальную шумовую часть на усредненный спектр опорного сигнала. Информативная часть спектра на Рис.7 представляет собой светло серое пятно в центре спектра. Вокруг него располагается темно серая область – шумовая часть нормированная на усредненный спектр опорного сигнала. В результате изображение успешно восстановлено.

 

а                                                                         б

Рис.7. Результат применения МОИ – восстановленное изображение а и его амплитудный спектр.б

 

         На первый взгляд кажется, что при инверсной фильтрации можно просто ограничиться областью, содержащей сигнал, а оставшуюся часть занулить. Фактически так и поступают при регуляризации, например по Тихонову или Винеру [3]. Только не убирают шум полностью, а делают его малым за счет умножения на малое число (или деления на большое). Однако для этого необходимо хорошо знать параметры шума. Отметим, что обычно предполагают его изотропным.

А что будет, если исходный сигнал будет уже содержать шум (в определении МОИ) причем анизотропный?

Возьмем в качестве исходного изображение, показанное на Рис.8.

Изображение на Рис.8 было получено из изображения, помещенного на Рис.1, путем добавления в спектр изображения прямоугольных областей, содержащих белый шум и записи полученного изображения в BMP файл.

 

а                                                      б

Рис.8. Исходное изображение, содержащее анизотропный шум - а и его амплитудный спектр - б.

 

На спектре на Рис.8 б шум хорошо виден в виде двух светлых прямоугольных областей. Произведем фильтрацию изображения Рис.8а с помощью аппаратной функции Гаусса при S=4.

 

 Рис.9. Расфокусированное изображение Рис.8 при S=4   и его амплитудный спектр.

 

Далее запишем изображение Рис.9а в BMP файл и считаем его.

 

Рис.10. Спектр расфокусированного изображения, помещенного на рис.9, после записи его в BMP файл и считывания из него.

 

Из Рис.9-10 хорошо видно, эти операции ( фильтрации и записью-чтением из файла ) шумовые области затронули незначительно, а высокочастотная информация об изображении сильно повреждена.

Произведем теперь инверсную фильтрацию, но полученные спектральные значения за пределами круга радиусом 40 пикселов занулим. Радиус этого круга выбирался исходя из визуально лучшего результата восстановления изображения.

 

а                                                                        б

Рис.11. Результат применения метода инверсной фильтрации при полном  удалении сигнала вне области радиуса R=40 Восстановленное изображение а и его амплитудный спектр - б

 

Из Рис.11 видно, что такая инверсная фильтрация позволила незначительно улучшить расфокусированное изображение – Рис.9. Однако оставшиеся неотфильтрованными области, содержащие шум, не позволили улучшить изображение.

Применение МОИ позволило это сделать ( см. Рис.12).

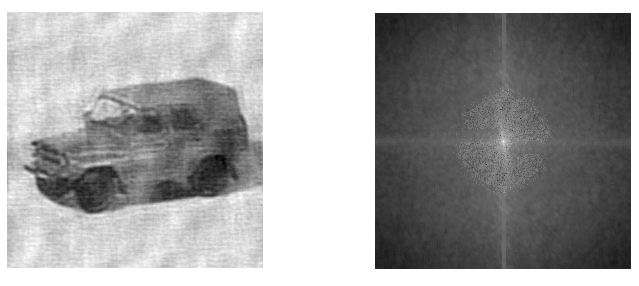
а                                                                         б

 

Рис.12. Результат применения МОИ. Восстановленное изображение а и его амплитудный спектр б.

 

Из Рис.12 видно, что применение МОИ позволяет получить лучший результат за счет правильного определения областей, содержащих шум на исходном изображении.

Таким образом, применение метода опорного изображения приводит к значительному улучшению качества вследствие учета априорной информации о свойствах формирующей оптической системы и выделения областей, содержащих шум произвольного происхождения при  последующей коррекции шума с учетом усредненного спектра опорного изображения.

 

Литература

1.     Р. Гонсалес,  Р. Вудс. Цифровая обработка изображений. М. «Техносфера» , 2005, 1071 стр.

2. Зражевский А.Ю., Кокошкин А.В., Новичихин Е.П., Титов С.В., «Повышение качества  радиоизображений». «Нелинейный Мир», № 9, 2010г., с. 582-590.

2.     Тихонов А.Н., Арсенин В.Я. - Методы решения некорректных задач.       М.Наука, 1979

3.     Зражевский А. Ю., Коротков В. А. Восстановление одномерных финитных сигналов, прошедших через фильтр низких частот. «Журнал Радиоэлектроники», №3, 2013г.

4.     Зражевский А. Ю., Коротков В.А. Восстановление искаженного оптической системой радиоизображения с помощью метода опорного изображения. Сб. Тезисы докладов IХ Всероссийский семинар по радиофизике миллиметровых и субмиллиметровых волн. С.122. Нижний Новгород. 2013.