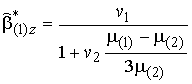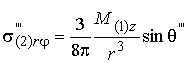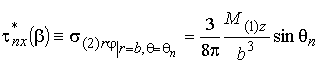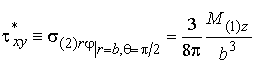УДК 539.3; 537.8

МАГНИТОДЕФОРМАЦИОННЫЙ ЭФФЕКТ ЭЛАСТОМЕРА С НАМАГНИЧЕННЫМИ ПОЛИДИСПЕРСНЫМИ СФЕРИЧЕСКИМИ ВКЛЮЧЕНИЯМИ

А. А. Паньков
Пермский национальный исследовательский политехнический университет

Статья получена 18 марта 2015 г.

Аннотация. На основе двухуровневых структурных математических моделей механики композитов исследован магнитодеформационный эффект ‑ уникальная способность эластомеров с магнитными микрочастицами к быстрым и контролируемым значительным деформациям в магнитных полях. Получено точное аналитическое решение для макроскопических и структурных магнитодеформационных полей, возникающих при изгибе цилиндрического полого консольного стержня с полидисперсной структурой из однонаправленно намагниченных сферических включений в эластомере во внешнем квазистатическом магнитном поле. Дано новое аналитическое решение для остаточной намагниченности композита и решение для деформационного поля в эластомере составной сферической ячейки от действия на включение вращающего магнитного момента. Обоснована и приведена постановка краевой задачи теории упругости для нахождения макроуровневых полей деформирования с формулировкой граничных условий в напряжениях на торцевой, внутренней и наружной боковых поверхностях полого цилиндрического консольного стержня с однородными эффективными упругими свойствами. Приведены расчетные схемы для решения этой задачи по теории упругости и в упрощенном виде для изогнутой оси полого стержня. Проведен анализ влияния объемной доли намагниченных сферических включений на изгибную деформативность композитного стержня. Установлен немонотонный характер этой зависимости и определены оптимальные значения объемной доли включений. Сделан вывод о необходимости выбора эластомера с высокой магнитной проницаемостью и малой жесткостью на растяжение.

Ключевые слова: магнитное поле, магнитоуправляемый эластомер, намагниченная структура, композит, эффективные свойства.

Abstract. On the basis of two-level structural mathematical models of mechanics of composites the magnetodeformation effect of unique ability of elastomers with magnetic microparticles to fast and controlled considerable deformations in magnetic fields is investigated. The exact analytical decision for the macroscopic and structural magnetodeformation fields arising at a bend of a cylindrical hollow console core with polydisperse structure from unidirectionally magnetized spherical inclusions in an elastomer in an external quasistatic magnetic field is received. The new analytical decision for residual magnetization of a composite and the decision for a deformation field in an elastomer of a compound spherical cell from action on inclusion of the rotating magnetic moment is given. Statement of a boundary-value problem of elasticity theory for finding of macro-level fields of deformation with the formulation of boundary conditions is proved and given in tension on face, internal and external lateral surfaces of a hollow cylindrical console core with uniform effective elastic properties. Settlement schemes for the solution of this problem on the elasticity theory and are provided in the simplified look for a curved axis of a hollow core. The analysis of influence of a volume fraction of the magnetized spherical inclusions on a flexural deformativnost of a composite core is carried out. Nonmonotonic nature of this dependence is established and optimum values of a volume fraction of inclusions are defined. The conclusion is drawn on need of a choice of an elastomer with high magnetic permeability and small rigidity on stretching.

Key words: magnetic field, magnetooperated elastomer, magnetized structure, composite, effective properties.

 

Введение

Магнитоуправляемые эластомеры представляют собой полимерные матрицы с внедренными в них магнитными частицами железа и его окислов нано и/или микро размера. Магнитные силы между частицами наполнителя соизмеримы с возникающими в податливом полимере упругими силами, что приводит к «магнитодеформационному эффекту» ‑ уникальной способности композита к быстрым и контролируемым значительным деформациям в магнитных полях [2‑8]. Магнитное поле действует на распределенные в эластомере намагниченные частицы и их смещения вызывают деформирование полимера и композита в целом [4]. Сделан вывод [5] о существенном влиянии на структурный механизм магнитодеформационного эффекта особенностей ближнего порядка пространственного расположения магнитных частиц в эластомерной матрице. Дополнительно отмечено наличие у магнитоэластомеров магнитореологического эффекта [6] и эффекта магнитоиндуцируемой пластичности или магнитной памяти формы [7, 8], например, для образцов мягкого силиконового эластомера, наполненного квазисферическими микрочастицами карбонильного железа.

Цель работы – обобщение известных аналитических решений для упругих [9] и пьезоупругих [10, 11] полидисперсных композитов на новый класс задач магнитоуправляемых структур с намагниченными полидисперсными сферическими включениями под воздействием внешнего магнитного поля.

1. Постановка задачи

Рассмотрим изгиб внешним магнитным полем  магнитоэластомерного двухфазного упругого полого цилиндрического стержня с однонаправлено намагниченными полидисперсными сферическими включениями (1-я фаза) в эластомере (2-я фаза). Магнитоупругие свойства фаз и композита изотропны. Размеры составных сферических ячеек – включений со сферическими оболочками из эластомера, намного меньше характерных размеров стержня и варьируются до бесконечно малых значений [9]. 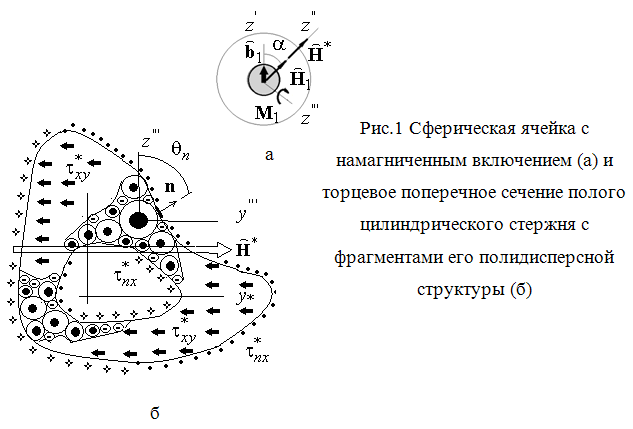Представительная ячейка ‑ сферическое включение с радиусом  и с вектором начальной магнитной индукции , окруженное концентрическим сферическим слоем радиуса  эластомера; относительная объемная доля 1-й фазы  в ячейке и в композите в целом,  (рис.1,а). Во всех ячейках полидисперсной структуры векторы начальной магнитной индукции  во включениях имеют одинаковую величину, ориентацию и лежат в плоскости ортогональной оси стержня . Вектор начальной магнитной индукции  составляет угол  с напряженностью  внешнего магнитного поля.

 

Объемный крутящий момент  одинаков для всех включений и не зависит от вариаций абсолютных размеров включений рассматриваемой полидисперсной структуры из однотипных сферических ячеек, так как  рассчитывается через векторное произведение

                                                   (1)

 

одинаковых для всех включений векторы намагниченности

                                              (2)

и магнитной индукции

                                                  (3)

внешнего поля для включений, где начальная намагниченность , магнитные восприимчивость  (2) и проницаемость  (3), вектор напряженности магнитного поля в сферических включениях  (2), (3), символ Кронекера , магнитная постоянная вакуума  Тл∙м/А [1]. Имеем зависимость

                                               (4)

между начальными намагниченностью  (2) и индукцией  включений. Для рассматриваемого случая изотропии магнитоупругих свойств (фаз и композита в целом) направления векторов напряженностей в фазах и на макроуровне  совпадают, поэтому , где коэффициент концентрации напряженности магнитного поля во включении

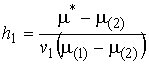                                         (5)

вычисляется через известное решение Хашина-Штрикмана [9] для эффективной магнитной проницаемости

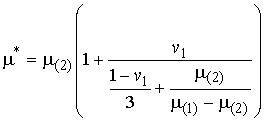                 (6)

композита, где магнитные проницаемости включений  и эластомера .

Таким образом, в сферических включениях вращательный объемный момент  (1) или

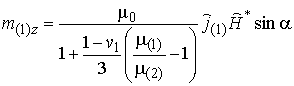,          (7)

с учетом (1)‑(6), начальная намагниченность

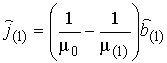                                    (8)

выражается через начальную магнитную индукцию.

Опуская промежуточные выкладки, приведем полученное новое аналитическое решение

                                               (9)

для эффективной остаточной магнитной индукции  композита с однонаправленно намагниченными полидисперсными сферическими включениями в эластомере, где коэффициент

,                                         (10)

объемная доля 2-й фазы .

2. Магнитоупругие поля в сферической ячейке

На основе принципа суперпозиции магнитные и деформационные упругие поля в сферической ячейке полидисперсной структуры цилиндрического полого стержня с намагниченными включениями представим суммой решений трех осесимметричных по осям , ,  (рис.1,а) задач:

1) расчет магнитного поля в ячейке через потенциалы

, ,

,

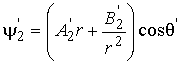от действия начальной намагниченности  по оси  включения (), где , константы интегрирования находим из условий непрерывностей потенциала  и индукции  на границе при  и условия  отсутствия внешнего магнитного поля:

,   ,

;

 

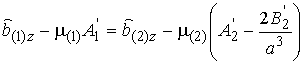2) расчет магнитного поля в ячейке

, ,

,

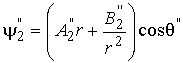от действия внешнего магнитного поля с напряженностью  по оси  () [9], константы интегрирования находим из условий

,   ,

;

 

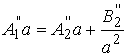3) расчет поля напряжений

                                          (11)

в сферическом слое эластомера  от действия на жесткое включение крутящего момента

                                               (12)

вокруг оси , обусловленного взаимодействием  и  при отсутствии перемещений внешних границ ячейки и, как следствие, отсутствие перемещений на всех внешних границах полого стержня в целом.

3. Макродеформирование композитного стержня и дополнительные упругие поля в ячейках

На основе решения (11) рассчитываем макроскопические реактивные неоднородные по окружной координате  и однородные по оси  осевые касательные напряжения

              (13)

на обеих цилиндрических поверхностях полого стержня с полидисперсной структурой из сферических ячеек в цилиндрической системе координат , , , ориентационный угол  нормали  к элементарной площадке  внутренней и внешней цилиндрических границ стержня; реактивные однородные поперечные касательные напряжения

                           (14)

на незакрепленном торцевом сечении () консольно закрепленного (в сечении ) полого стержня (рис.1,б) с учетом (11), ось стержня лежит на оси . Отметим, что на рис.1,б символами (•) и () отмечены участки поверхностей, на которых касательные напряжения  (13) направлены к нам (против оси ) и от нас (по оси ) соответственно. Напряжение  изменяется лишь по внутреннему и внешнему контурам полого сечения, как функция угла  и постоянны по длине стержня без зависимости от . Напряжение  равно нулю и меняет направление на обратное во всех точках контуров полого сечения, в которых касательные параллельны оси . На торцевой незакрепленной границе полого стержня касательные напряжения  (14) постоянны по всей этой границе, не зависят от геометрии поперечного сечения и направлены против оси .

Решение этой новой задачи об изгибе композитного стержня действующими на его внешних границах касательными напряжениями ,  получим из последовательного решения двух задач теории упругости на макро и микро уровнях:

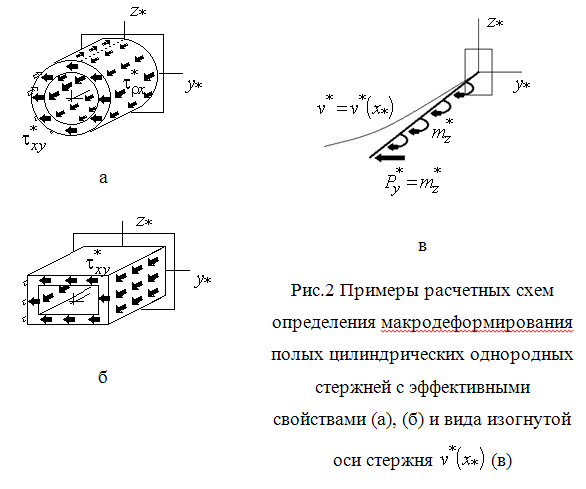
- расчет поля макронапряжений  в полом консольном стержне с эффективными упругими свойствами от действия касательных напряжений , , , (рис.2,а,б), например, на основе методов в [12];

- расчет по «трехфазной модели» ‑ составной сферической ячейке в эффективной упругой среде [9] поля напряжений в составной сферической ячейке для найденных ранее значений макронапряжений  в точке  стержня через известное [9] поле концентраций напряжений в ячейке.

 

В частном случае, для полого осесимметричного цилиндрического стержня с кольцевым поперечным сечением (рис.2,а) касательные напряжения на боковой поверхности

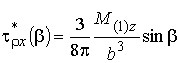                                          (15)

в цилиндрической системе координат , ,  с учетом равенства ; на торцевой незакрепленной границе стержня касательные напряжения  (14). От касательных напряжений  (13) с одинаковыми значениями на внутренней и внешней цилиндрических поверхностях полого стержня можно перейти к распределенному по длине стержня изгибающему моменту с интенсивностью

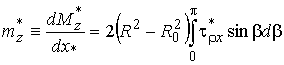                     (16)

и от касательных напряжений  (14) на незакрепленной при  торцевой границе стержня – к результирующей поперечной силе

                                               (17)

где внутренний  и внешний  радиусы кольцевого поперечного сечения стержня. Из (16), (17) с учетом (14), (15) следует равенство

                                   (18)

Таким образом, в произвольном с координатой  поперечном сечении полого стержня действует результирующий изгибающий момент

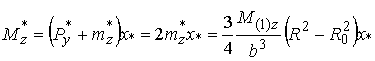
или

                                     (19)

с учетом (18) и связи (12) объемной плотности вращающего момента  в сферических включениях с результирующим вращающим моментом . Отметим, что решение (19) в точности совпадает с результирующим (по «отсеченной» сечением с координатой  области  стержня) моментом

,

где объем включений  и объем отсеченной части  длиной . Выполняется равенство

,                                  (20)

связывающее эффективный распределенный по длине стержня изгибаюший момент с интенсивностью  с плотностью  объемного крутящего магнитного момента с учетом (18), (19).

Изгибающий момент  (19) обуславливает возникновение кривизны  оси стержня, решение для эффективного модуля Юнга  композита дано в [9], осевой момент инерции  кольцевого поперечного сечения.

В результате получим решение

                   (21)

для градиента кривизны оси полидисперсного композитного полого стержня во внешнем магнитном поле, где зависимость от объемной доли  намагниченных сферических включений определяется концентрационной функцией

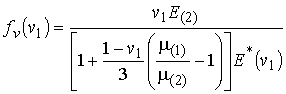,                     (22)

зависимость  от параметра  ‑ функцией

, .

Решение для изогнутой оси стержня

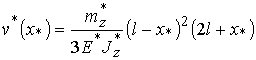
или

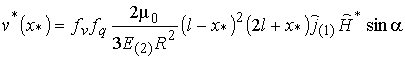
с учетом (20)‑(22).

4. Численный расчет

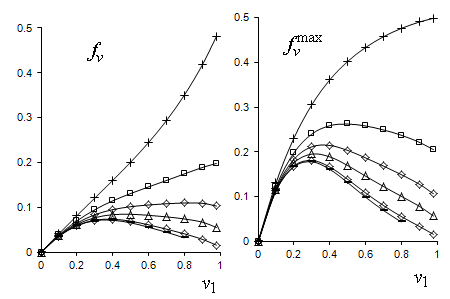
На рис.3,а представлены результаты расчета функции  (22) при коэффициентах Пуассона изотропных включений =0.1 и матрицы =0.45, отношения модулей Юнга  и магнитных проницаемостей  фаз.

 

а                                                   б

Рис. 3 Зависимости интенсивности изгиба  от объемной доли  включений,

параметр = 1000 (), 100 (), 20 (), 10 (), 5 (), 2 (+)

Видно (рис.3,а), что максимальный градиент  кривизны оси полидисперсного композитного стержня с намагниченными включениями во внешнем магнитном поле немонотонно изменяется от величины объемной доли включений  и максимальные значения  достигаются при 0.3, например, для жестких (), () и при 0.7 для менее жестких () включений. При малом () различии упругих свойств включений и матрицы зависимость величины  от  становится монотонно возрастающей (), (+). Отметим, что для магнитоэластомера имеет место сильное различие в упругих свойствах жестких намагниченных включений и податливой эластомерной матрицы [2].

Для повышения изгибной податливости стержня во внешнем магнитном поле необходимо выбирать для матрицы композита низкомодульный эластомер с высокой магнитной проницаемостью, так как выполняется неравенство для производной  функции  (22) для всех значений , . Для предельного случая  из (22) получим (рис.3,б)

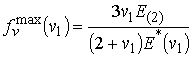                                        (23)

Из сравнения соответствующих кривых:  (22) на рис.3,а и  (23) на рис.3,б, например, для магнитоэластомера с жесткими () намагниченными сферическими включениями при оптимальной объемной доле 0.3 следует, что повышением магнитной проницаемости эластомера можно примерно в 3 раза увеличить изгибную деформируемость композитного стержня во внешнем магнитном поле.

Заключение

Получено точное аналитическое решение для макроскопических и структурных магнитодеформационных полей, возникающих при изгибе цилиндрического полого консольного стержня с полидисперсной структурой из однонаправленно намагниченных сферических включений в эластомере во внешнем квазистатическом магнитном поле. Дано новое аналитическое решение (9), (10) для остаточной намагниченности такого композита и решение (11) для деформационного поля в эластомере составной сферической ячейки от действия на включение вращающего магнитного момента. Обоснована и приведена постановка краевой задачи теории упругости для нахождения макроуровневых полей деформирования с формулировкой граничных условий в напряжениях (13)‑(15) на торцевой, внутренней и наружной боковых поверхностях полого цилиндрического консольного стержня с однородными эффективными упругими свойствами [9]. Приведены расчетные схемы (рис.2,а,б) для решения этой задачи в рамках теории упругости и в упрощенном виде (рис.2,в) для изогнутой оси полого стержня. Проведен анализ влияния объемной доли намагниченных сферических включений на изгибную деформативность композитного стержня во внешнем магнитном поле. Установлен (рис.3) немонотонный характер этой зависимости и определены оптимальные значения объемной доли включений. Сделан вывод о необходимости выбора эластомера с высокой магнитной проницаемостью и малой жесткостью на растяжение.

Работа выполнена при финансовой поддержке гранта РФФИ № 14-01-96004 р_урал_а.

 

Литература

1.      Вонсовский С.В. Магнетизм. Магнитные свойства диа-, пара-, ферро-, антиферро- и ферримагнетиков. ‑ М.: Наука, 1971. ‑1032 с.

2.      Чертович А.В., Степанов Г.В., Крамаренко Е.Ю. Магнитоуправляемые эластомеры: синтез, свойства, применение // XVII Зимняя школа по механике сплошных сред: сборник статей Международной научной конференции. ‑ Пермь, 2011. – С. 328

3.      Chertovich A.V., Stepanov G.V., Kramarenko E.Yu., Khokhlov A.R. New Composite Elastomers with Giant Magnetic Response // Macromolecular Materials and Engineering, 2010, Vol. 295, pp. 336

4.      Stolbov O. V., Raikher Yu. L., Balasoiu M. Modelling of magnetodipolar striction in soft magnetic elastomers // Soft Matter., 2011, No 7. ‑ pp. 8484-8487

5.      Райхер Ю. Л., Столобов О.В. Моделирование магнитострикционных деформаций в мягких магнитных эластомерах // Вычисл. механика сплошных сред, 2009, № 2. – С. 85-95

6.      Столбов О. В., Райхер Ю. Л., Степанов Г. В., Чертович А. В., Крамаренко Е. Ю., Хохлов А. Р. Низкочастотная реология магнитоуправляемых эластомеров с изотропной структурой // Высокомолекулярные соединения. Серия А, 2010, № 12. – С. 2158-2169

7.      Melenev P., Raikher Yu., Stepanov G., Rusakov V., Polygalova L. Modeling of the field-induced plasticity of soft magnetic elastomers // J. Intelligent Material Systems and Sructures, 2011, Vol. 22. – pp. 531-538

8.      Меленёв П. В., Райхер Ю. Л., Русаков В. В. Пластичность мягких магнитных эластомеров // Высокомолекулярные соединения. Серия А, 2010, № 4. – С. 628-633

9.      Кристенсен Р. Введение в механику композитов. ‑ М.: Мир, 1982. ‑ 334 с.

10.  Паньков А.А. Эффективные свойства намагниченных структур с полидисперсными сферическими включениями // Журнал радиоэлектроники: электронный журнал, 2014, №6 . URL: http://jre.cplire.ru/jre/jun14/4/text.pdf

11.  Pan’kov A.A. Correlation functions and piezoelektromagnetic properties of structures on the method of correlation components // Mechanics of Composite Materials, 2014, Vol. 50, No 6. ‑ pp.681-694

12.  Лехницкий С.Г. Кручение анизотропных и неоднородных стержней. – М.: Наука, 1971. – 240 с.