УДК 535.31; 001.891.573

Метод оптико-геометрического моделирования в  задаче определения габаритных и отражательных характеристик космических аппаратов

 

В. Р. Ахметьянов, И. О. Лутов, М. И. Олейников

Военно-космическая академия имени А.Ф. Можайского

 

Статья получена 16 апреля 2015 г.

 

Аннотация. В статье рассматривается метод оптико-геометрического моделирования в задаче определения габаритных и отражательных характеристик космических аппаратов, которые после  окончания срока активного существования переходят в разряд космического мусора и требуют непрерывного контроля, в том числе, наземными оптико-электронными средствами. Оптико-геометрическая модель включает в себя геометрическое описание космического аппарата как трехмерного тела, состоящего из функционально - конструктивных элементов (ФКЭ), и оптические характеристики материалов и покрытий ФКЭ. Для ряда космических аппаратов имеются исходные видовые данные, представляющие собой цифровые фотографические изображения, которые предъявляются разработчиками на этапе монтажных и испытательных работ. Относительные геометрические характеристики космического аппарата могут быть получены из анализа цифрового изображения. С этой целью предлагается использовать компактный алфавит геометрического описания контурной модели конструкции космического аппарата в виде совокупности примитивов, отображаемых на исходное изображение с учетом свойств центрального проецирования объекта наблюдения на картинную плоскость. Полученные оценки геометрических параметров космического аппарата позволяют осуществить анализ его отражательных характеристик с помощью математической модели численно-аналитического расчета в видимом диапазоне, которая основана на представлении космического аппарата в виде набора геометрических примитивов конического, сферического и плоского типов. В качестве модели отражения поверхности принята модель отражения Ламберта – Фонга, представляющая отраженное поверхностью излучение в заданных направлении и спектральном диапазоне в виде суммы двух независимых компонент, имеющих диффузный и зеркальный характер отражения. Предложенный в статье подход иллюстрируется на примере изображения космического аппарата «Космический телескоп Хаббла», полученного в 2009 году в ходе космического эксперимента «Атлантис» STS-125.

Ключевые слова: космический аппарат, космический мусор, оптико-электронные средства, геометрические характеристики, оптические характеристики материалов и покрытий.

Abstract. In the article the method of optical-geometrical modeling in a problem of definition of the dimensional and reflective characteristics of spacecraft is considered. After ending term of fissile existence spacecraft passes in the category of space debris and requires continuous check, including ground-level optical-electronic means. The optical-geometrical model includes the geometrical description of spacecraft as three-dimensional body composed from functional - constructive elements (FCE), and optical characteristics of materials and covers FCE. For a number of spacecraft there are source specific data representing digital photographic images, which one are presented by the developers at a stage of assembly and test operations. The relative geometrical performances of spacecraft can be received from analysis of the digital image. With this purpose it is offered to use the compact alphabet of the geometrical description of the contour pattern of a construction of spacecraft by the way collections of primitives mapped on the source image with allowance for of properties of a central projection of object of supervising on a picture plain. The received estimations of geometrical arguments of spacecraft allow to realize analysis of his reflective characteristics with the help of a mathematical model of numerically - analytical account in a visible band, which one is based on submission of spacecraft by the way of set of geometrical primitives of conical, spherical and flat types. As the pattern of reflex of a surface the pattern of reflex of a Lambert - Fong, exhibiting by a reflected surface radiating in a given direction and spectral range by the way sums two independent a components having diffuse and reflecting nature of reflex is accepted. The approach, offered in the article, is illustrated on an example of the image of spacecraft «Hubble Space telescope», received in 2009 during space experiment «Atlantis» STS-125.

Keywords: a spacecraft, space debris, optical-electronic means, geometrical characteristics, optical characteristics of materials and covers.

 

Выводимые на околоземную орбиту космические аппараты (КА) после окончания срока активного существования переходят в разряд космического мусора, требующего непрерывного контроля [1]. Для наблюдения космических аппаратов наземными оптико-электронными средствами (ОЭС) необходимо наличие оптических характеристик, позволяющих осуществлять надежное обнаружение и сопровождение КА, движущихся по орбитальным траекториям. Для ряда КА имеются исходные видовые данные, представляющие собой цифровые фотографические изображения. Эти изображения предъявляются разработчиками КА на этапе монтажных и испытательных работ, проводимых, в том числе, в условиях открытого космоса. Для получения оптических характеристик может быть использована трехмерная оптико-геометрическая модель (ОГМ) КА, определенная в работе [2].

Оптико-геометрическая модель включает в себя геометрическое описание КА как трехмерного тела, состоящего из функционально-конструктивных элементов (ФКЭ), и оптические характеристики материалов и покрытий ФКЭ. Относительные геометрические характеристики КА могут быть получены из анализа его изображения, представляющего собой двумерную проекцию трехмерного тела на картинную плоскость. Для этой цели возможно использование контурных рисунков, построенных с помощью структурированных геометрических моделей анализируемых объектов [3, 4]. Метрическая информация о КА в ряде случаев извлекается из габаритных ограничений на полезную нагрузку, которая выводится на орбиту ракетой-носителем.    Используемые ракеты-носители, как правило, являются адаптированными для КА заданного типа. В этом случае применимы методы калибровки изображений, основанные на совмещении объекта съемки и тест – объекта с калибровочными марками, размещенными в узлах пространственной решетки [5].

Рассмотрим основные свойства изображения, получаемого при центральном проецировании объекта наблюдения на картинную плоскость [4, с. 125-129]. Проецирование трехмерного объекта осуществляется с помощью прямых проецирующих лучей, которые называются проекторами. Они выходят из центра проекции, проходят через каждую точку объекта и, пересекая картинную плоскость, образуют проекцию. Так как проекция отрезка сама является отрезком, то достаточно спроектировать лишь конечные точки.

При фотографировании объекта картинная плоскость перпендикулярна оптической оси объектива. Для этого случая введем систему декартовых координат в объектном пространстве, связанную с картинной плоскостью следующим образом. Ось абсцисс OX расположена по горизонтали (в плоскости местного горизонта), ось ординат OY расположена по вертикали картинной плоскости. Ось аппликат OZ совпадает с оптической осью объектива, направлена в сторону наблюдателя и вместе с осями OX и OY образует правую систему координат (СК). Центр СК OXYZ расположен в точке пересечения оси OZ и ортогональной плоскости OXY, проходящей через некоторую опорную точку (ОТ) объекта наблюдения. Обозначим аппликату центра проекции как  (), а координаты опорной точки в плоскости OXY как . Тогда для любой точки , принадлежащей проектору, который пересекает плоскость OXY в точке , и имеющей  соблюдаются следующие соотношения [4, с. 134]:

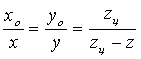.                                                                    (1)

Исходя из (1) смещения проективных координат  относительно координат  определяются как

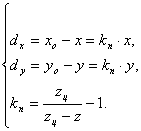                                                                     (2)

С учетом того, что координаты  являются результатом параллельного проецирования произвольной точки проектора на плоскость OXY, то выражение (2) позволяет осуществлять переход от параллельной проекции трехмерного объекта к центральной проекции в определенной выше системе координат OXYZ. Обозначим координаты точки в картинной плоскости как . Исходя из равного масштаба по координатным осям картинной плоскости, соотношения между координатами  и  определяется следующим образом:

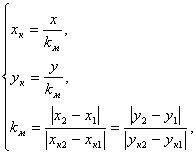                                                          (3)

где  - масштабный коэффициент,

       и  - координаты концевых точек отрезка в объектном пространстве,

       и  - координаты точек проекции отрезка в картинной плоскости.

Для построения трехмерной оптико-геометрической модели КА используются геометрические примитивы. Каждый примитив размещается в строительной системе координат (ССК) с осями, направленными аналогично осям СК OXYZ, и имеет следующие общие параметры:

-       координаты центра (опорной точки) примитива ;

-       углы разворота ССК: вокруг оси OX , вокруг оси OY , вокруг оси OZ ;

-       дополнительное смещение центра примитива: по оси OX , по оси OY , по углу вокруг оси OZ .

Все примитивы по типу формообразующей поверхности разделяются на две группы, образованные плоскими фигурами и поверхностями второго порядка. Основу плоских фигур составляют:

-                              прямоугольник шириной  с размером  по глубине, лежащий в плоскости OXZ и определенный концевыми точками со следующими координатами: , , , ;

-                              треугольник, лежащий в плоскости OXZ и заданный концевыми точками со следующими координатами: , , ;

-                              круг, лежащий в плоскости OXZ, имеющий радиус  и центр, расположенный в центре ССК.

В случае прямоугольника и круга центр примитива совпадает с центром ССК. У треугольника две точки одной стороны лежат на оси OX. При этом точка с координатами  центра ССК является опорной, а параметры  позволяют построить фигуру с произвольными размерами и ориентацией сторон, не лежащих на оси OX. В ряде случаев целесообразно использовать производный от круга примитив – сегмент, ограниченный начальным и конечным центральными углами, отсчитываемыми от оси OX.

С помощью прямоугольника и треугольника могут быть построены два объемных примитива, представляющих собой прямые призмы:

-                              параллелепипед с основаниями в виде прямоугольников, лежащих в параллельных плоскостях, пересекающих ось OY в нулевой точке и точке с ординатой ;

-       треугольную призму с треугольными основаниями, пересекающими ось OY в нулевой точке и точке с ординатой .

-       На основе круга может быть построен примитив, называемый обобщенным конусом (далее просто конусом) и объединяющий три объемных фигуры:

-                              усеченный прямой круговой конус с основанием радиуса  в плоскости OXZ и с основанием радиуса  в плоскости, которая пересекает ось OY в точке с ординатой ;

-                              прямой круговой конус высотой   с основанием радиуса  в плоскости OXZ, имеющий в параметрах усеченного конуса ;

-                              цилиндр высотой  , который в параметрах усеченного конуса имеет .

С помощью круга также может быть построен примитив, называемый обобщенной сферой (далее просто сферой) и объединяющий две объемные фигуры:

-                              сферу радиуса  с центром, расположенным в центре ССК;

-                              шаровой сегмент высотой , хорда которого пересекает ось OY в точке с ординатой  и который при высоте  превращается в сферу.

Кроме того, если вписать в круг правильный  – угольник (), то получится производный примитив, с помощью которого, в свою очередь, можно сформировать следующие объемные фигуры:

-                              на основе (обобщенного) конуса: усеченную (правильную) пирамиду с , пирамиду с , (правильную) призму с ;

-                              на основе шарового сегмента высотой  - фигуру типа зонтик.

Заданные выше примитивы позволяют построить в терминах функционально-конструктивных элементов геометрическое описание космического аппарата в целом. Назовем объединенный элемент трехмерного представления - конструкцией КА. Для отображения трехмерной геометрии на картинную плоскость конструкция КА определяется следующей группой параметров , где  - углы разворота строительной системы координат конструкции КА в целом относительно опорной точки, положение которой в проективной системе координат OXYZ задается параметрами: .

Совокупность определенных выше примитивов вместе с объединенным элементом можно трактовать как компактный алфавит геометрического описания контурной модели конструкции КА. Предложенный алфавит обладает свойством информационной полноты геометрического описания конструкции КА, ограниченного погрешностью метрического представления ФКЭ. В тоже время, задача оценки группы параметров  относится к классу обратных некорректных задач, характеризующихся наличием, как статистических погрешностей оценок параметров, так и достаточно значимой неопределенностью исходных данных. Именно поэтому в работе [5, с. 87,88] в качестве решения данной задачи предлагаются методы обратной пространственной засечки и построения одиночных объектных моделей методами последовательных приближений.

Из рассмотрения свойств изображения, получаемого при центральном проецировании объекта наблюдения на картинную плоскость, следует, что проекция отрезка сама является отрезком. Поэтому, в качестве маркеров для совмещения объекта съемки и геометрической модели могут выступать концевые точки примитивов, характеризующих положение пространственных осей КА. Для этой цели наиболее подходит параллелепипед, если КА имеет явно выраженные габариты блока служебных систем, как правило, называемого корпусом КА. Другим подходящим примитивом является прямоугольник в случае наличия у КА солнечных батарей. Одна из точек выбранного примитива служит в качестве опорной точки, относительно которой строится как «опорный» примитив, так и остальные элементы геометрического описания контурной модели конструкции КА. Тем самым устраняется пространственный сдвиг контурной модели относительно изображения объекта наблюдения в картинной плоскости и создаются предпосылки для последующего устранения неопределенности в ракурсе и масштабе модели конструкции КА.

Исходя из сказанного, методика совмещения объекта съемки и контурной модели конструкции КА включает следующие этапы:

1)       Выбор опорной точки и геометрического примитива, позволяющего в  наибольшей степени отобразить на картинную плоскость трехмерные характеристики доминирующего ФКЭ конструкции КА.

2)       Последовательное совмещение контурной модели опорного примитива и изображения объекта наблюдения посредством изменения масштабного коэффициента  и параметров ракурса  конструкции КА относительно опорной точки.

3)      Определение параметров  проецирования объекта наблюдения на картинную плоскость и дальнейшее согласование с ним контурной модели опорного примитива с учетом изменения параметров масштаба  и ракурса .

4)       Последовательное задание параметров, описывающих геометрические размеры и ракурсы примитивов наиболее значимых ФКЭ, которые определяются детальностью представления конструкции объекта, и проведение согласования каждого примитива с изображением КА.

 

Рисунок 1 – Изображение КА «Космический телескоп Хаббла»

Рассмотрим применимость предложенной методики на примере изображения  КА «Космический телескоп Хаббла» («КТХ»). Вид КА «КТХ» с борта космического корабля «Атлантис» STS-125 (2009 г.) [6] показан на рисунке 1. Целью использования предложенной методики будем считать определение геометрических размеров блока служебных систем (корпуса), солнечных батарей КА и экрана бленды. Так как корпус рассматриваемого КА имеет явно выраженную форму цилиндра (диаметр 4,3 м), то в качестве объекта для совмещения подходит «кормовая» часть корпуса. В центр торцевой поверхности цилиндра можно поставить опорную точку, положение которой показано на рисунке 2 крестом.

Последовательное совмещение контурной модели опорного цилиндра и изображения объекта наблюдения посредством изменения масштабного коэффициента и параметров ракурса конструкции КА относительно опорной точки приводит к следующим их значениям: , . Определение параметров проецирования объекта наблюдения на картинную плоскость и дальнейшее согласование с ним контурной модели опорного примитива с учетом изменения параметров масштаба и ракурса позволяет получить следующие значения . Положение точки, соответствующей данным координатам в картинной плоскости, показано на рисунке 2 вторым крестом, находящемся на цилиндрической поверхности средней части корпуса. В результате совмещения по параметрам проецирования, показанном на рисунке 3, получаются дальнейшее согласование цилиндрических примитивов, описывающих среднюю часть корпуса и бленду. В дальнейшем уточнения параметров проецирования, как правило, не требуется.

 

Рисунок 2 – Опорная точка на изображении КА

Рисунок 3 – Совмещение опорного примитива по масштабу и ракурсу

На рисунке 3 также показан результат совмещения изображения и примитивов, соответствующих солнечным батареям и описываемым прямоугольниками с параметрами , по геометрическим размерам, ракурсу и положению относительно опорной точки. Одна солнечная батарея состоит из двух фрагментов с размерами . Геометрические параметры экрана бленды определяются в результате согласования двух плоских примитивов: прямоугольника и сегмента круга (рисунок 3). Эквивалентный экрану бленды по площади прямоугольник имеет следующие геометрические параметры . Так как целью использования предложенной методики было определение геометрических размеров корпуса, солнечных батарей КА и экрана бленды, то для описания конструкции объекта оказалось достаточным применение трех примитивов: прямоугольника, сегмента круга и конуса.

Полученные оценки геометрических параметров КА позволяют осуществить анализ его отражательных характеристик с помощью математической модели численно-аналитического расчета в видимом диапазоне, которая основана на представлении КА в виде набора геометрических примитивов конического, сферического и плоского типов. В качестве модели отражения поверхности может быть принята модель отражения Ламберта – Фонга, представляющая отраженное поверхностью излучение в заданном направлении в спектральном диапазоне  в виде суммы двух независимых компонент [7, 8]:

,                                                (4)

где   – сила диффузно и зеркально отраженных излучений объекта, соответственно.

Диаграмма отражённого излучения аппроксимируется функцией y=cos^pa. Показатель степени p определяется при задании значения полу угла расходимости зеркального отражения α на уровне 0.5 по формуле:

.                                                                 (5)

При p=1 реализуется модель Ламберта, при p >>1 – модель Фонга. Для зеркального отражения величина  составляет единицы градусов. Направление максимума зеркально отраженного излучения определяется законом отражения геометрической оптики.

Тогда, выражение для силы диффузно-отраженного излучения будет иметь вид:

,                                                 (6)

где        – плотность падающего на объект солнечного потока в заданном диапазоне;

         S       – площадь элементарной площадки (ЭП);

            – косинус угла между вектором на Солнце и нормалью ЭП;

          – косинус угла между вектором на наблюдателя и нормалью ЭП.

Для силы зеркально-отраженного излучения:

,                                               (7)

где     – косинус угла между зеркальным вектором на Солнце и нормалью ЭП;

          – нормирующий множитель.

На рисунке 4 обозначены углы, определяющие направления на Солнце и на наблюдателя в  орбитальной системе координат (ОСК) [9]: начало – в центре масс КА, ось Z_О нормальна плоскости орбиты КА и коллинеарна вектору  кинетического момента движения КА (вектор интеграла площадей), ось Y_О направлена по радиус-вектору КА в сторону его возрастания, а ось X_О дополняет систему до правой. С учётом этого получим выражения направляющих косинусов для Солнца и наблюдателя:

, , ,                            (8)

, ,.                            (9)

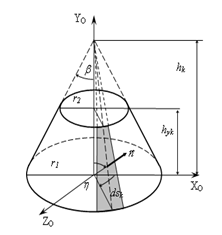
Для расчёта отражённого излучения конических поверхностей были определены их геометрические параметры (рисунок 5): положение и ориентация в ОСК и геометрические размеры (радиус нижнего и верхнего оснований и высота). Выражения для направляющих косинусов нормалей к элементарным площадкам имеют вид:

, , ,                             (10)

где .

Рисунок 4 – Углы, определяющие направление на Солнце и на наблюдателя в ОСК	Рисунок 5 – Параметры конуса, усечённого конуса, цилиндра

 

Сила диффузно и зеркально отраженного от поверхности конуса излучения Солнца определяется уравнениями:

,                                  (11)

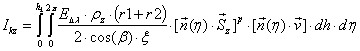.                                (12)

 

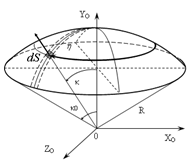
Рисунок 6 – Параметры сферы

 

Для расчёта отражённого излучения сферических поверхностей были определены их геометрические параметры (рисунок 6): ориентация в ОСК и геометрические размеры (радиус и высота усечения). Выражения для направляющих косинусов нормалей к элементарным площадкам имеют вид:    

, , ,                         (13)

где    , κ_о – центральный полу угол шарового сегмента (для сферы κ_о=π).

Площадь элементарной площадки с координатами η, κ определяется соотношением:

.                                                          (14)

Сила диффузно и зеркально отраженного от поверхности сегмента излучения Солнца определяется уравнениями:

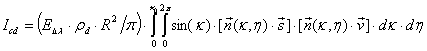,         (15)

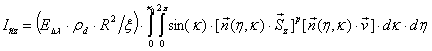.        (16)

 

В случае, когда требуется рассчитать отражённое излучение от полной сферы, незатенённой и неэкранированной другими элементами конструкции, то в таких случаях необходимо использовать значительно более простые расчётные аналитические соотношения:

,    .     (17)

Выражение для расчёта силы излучения от КА в целом можно представить в следующем виде:

                   (18)

где    – оператор диффузного отражения элемента конструкции;

                  – оператор зеркального отражения элемента конструкции.

 

Представленный подход к расчёту отражательных характеристик КА был реализован в программно-моделирующем комплексе (ПМК), который позволяет решать задачи построения ОГМ КА и расчёта на их основе характеристик отражения в видимом и ближнем ИК диапазонах.

 

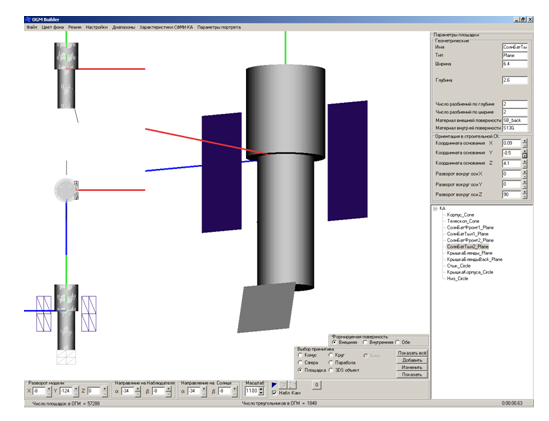
Рисунок 7 – Построение ОГМ КА

На рисунке 7 представлен вид главного окна ПМК (включен режим конструктора ОГМ), на котором отображена построенная ОГМ «Космического телескопа Хаббла», рассматриваемого в данной статье. Построение модели было осуществлено с учётом примитивов и их размеров, определённых по результатам анализа изображений.

Непосредственно анализ отражательных характеристик данного КА можно провести по результатам расчёта пространственного распределения отражённого Солнечного излучения в зависимости от ракурса наблюдателя при заданном положении источника подсветки – Солнца. На рисунке 8  приведена главная экранная форма ПМК в режиме расчёта отражённого излучения.

 

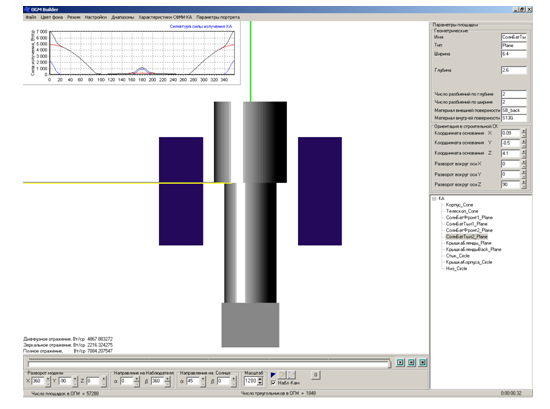
Рисунок 8 – Расчёт отражённого излучения
КА «Космический телескоп Хаббла»

В качестве условий расчёта были выбраны следующие (рисунок 4):

‑ углы разворота КА равны нулю;

‑ спектральные диапазоны Δl₁= 0.39…0.49 мкм, Δl₂= 0.51…0.59 мкм и Δl₃= 0.595…0.805 мкм, соответствующие фильтрам BVR стандартной фотометрической системы Джонсона;

‑ положение Солнце определено углами β_s=0⁰, α_s=45⁰;

‑ положение наблюдателя определено углами β_v=0⁰…360⁰, α_v=45⁰.

За счёт использования диапазона углов реализуется возможность построения и анализа срезов пространственных объёмных индикатрис анализируемого КА.

На рисунке 9 приведена иллюстрация индикатрисы отражённого излучения КА «Космический телескоп Хаббла», совмещённая с его ОГМ и сеткой углов β_s. Для удобства анализа результатов расчёта на рисунке 9 изображение КА повёрнуто на 90⁰ так чтобы плоскость среза сечения индикатрисы совпадала с плоскостью листа.

 

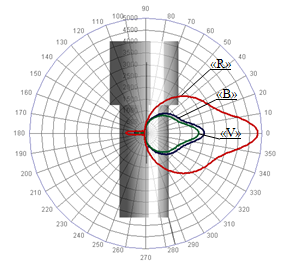
Рисунок 9 – Индикатриса отражённого излучения
КА  «Космический телескоп Хаббла»

 

Анализ среза приведённой индикатрисы позволяет сделать выводы о том, что для заданных условий подсветки и наблюдения отражение носит преимущественно диффузный характер. Увеличение энергии отражённого сигнала для углов β_v близких к 0⁰ и 180⁰ обусловлено наличием зеркального отражения от цилиндрического корпуса КА. Неравномерное распределение энергии по спектрам отражения в большей мере определяется тем, что диапазон «R» имеет наибольшую ширину.

В заключение отметим, что предложенный метод оптико-геометрического моделирования позволяет оценить отражательные характеристики движущихся по орбитальным траекториям космических аппаратов, сведения о которых весьма ограничены. Получаемые оценки отражательных характеристик, в свою очередь, дают возможность осуществлять надежное обнаружение и сопровождение наблюдаемых с помощью оптико-электронных средств как активных, так и выведенных из эксплуатации КА. Таким образом, благодаря разработанной методике решена одна из частных задач в проблеме экологического мониторинга ближнего космоса.

 

Литература

1         Назаренко А.И. Моделирование космического мусора / Серия «Механика, управление и  информатика». - М.: ИКИ РАН, 2013. – 216 с.

2         Корякин А.В., Лутов И.О. Распознавание космических объектов по разнородной видовой информации.- СПб.: ВИКУ, 2000.- 115 с.

3         Прэтт У. Цифровая обработка изображений: Пер. с англ.- М.: Мир, 1982.- Кн. 2.- 480 с.

4         Сиденко Л.А. Компьютерная графика и геометрическое моделирование: Учебное пособие.- СПб.: Питер, 2009.- 224 с.

5         Дубиновский В.Б. Калибровка снимков.- М.: Недра, 1982.- 224 с.

6         Космический телескоп «Хаббла». Международный научный сервер. - Htpp: // Scientificru.

7          Борн, М Основы оптики  / М. Борн, Э. Вольф; перевод с англ. – 2‑е изд. – М.: Наука, 1973. – 720 с.

8         Bui Tuong Phong Illumination for Computer Generated Pictures // Image Processing Editor University of Utah № 6 Vol. 18 1975 pp. 311 – 317.

9         Основы теории космического полёта : справочник / Г.С. Нариманов [и др.]; под. ред. Г.С. Нариманова и М.К. Тихонравова. – М.: Машиностроение, 1972. – 608 с.