| "ÆÓÐÍÀË ÐÀÄÈÎÝËÅÊÒÐÎÍÈÊÈ" "JOURNAL OF RADIOELECTRONICS" N 4, 1999 |
On mode dispersion properties of chiral optical planar waveguides
S.V. Demidov* , K.V. Kushnarev* , V.V. Shevchenko**
*Radiophysics Department , Russian People Friendship University ,
Mikluho-Maklay str. 6, Moscow 117198 , Russia
**Institute of Radioengineering and
Electronics of Russian Academy of Sciences,
Mokhovaya str.11, Moscow 103907, Russia
Received April 28, 1999.
1. Introduction
Functions ![]() and
and ![]() are used instead of fields
are used instead of fields ![]() and
and ![]() during studying and
constructing modes in planar waveguides . They are related to each other by expressions
during studying and
constructing modes in planar waveguides . They are related to each other by expressions
![]() (1)
(1)
where ![]() . At the same time
Drude-Born-Fedorv constitutive relations for the chiral media are taken as
. At the same time
Drude-Born-Fedorv constitutive relations for the chiral media are taken as
![]() ,
,![]() (2)
(2)
where ![]() ,
, ![]() are permittivity and permeability of the medium ,
are permittivity and permeability of the medium , ![]() is a chiral parameter [1-4]. Equations for
functions
is a chiral parameter [1-4]. Equations for
functions ![]() and
and ![]() can be obtained from Maxwell's equations as
can be obtained from Maxwell's equations as
![]() ,
, ![]() (3)
(3)
where
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() (4)
(4)
![]() - velocity of light in vacuum and
- velocity of light in vacuum and ![]() . Frome (1) the boundary conditions are
. Frome (1) the boundary conditions are
![]() ,
, ![]() (5)
(5)
Here index ![]() refers to the tangential
field components on the boundaries.
refers to the tangential
field components on the boundaries.
It is important to notice that in the boundless chiral medium the solutions of the equations (3) describe planar waves with right- and left-handed circular polarisation respectively .
2. Symmetrical planar waveguide
Let us consider symmetrical planar waveguide as a two-dimensional model of an optical fiber (Fig. 1) .
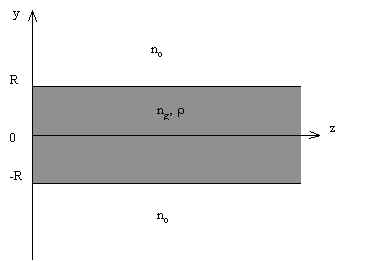
Fig.1. Symmetrical planar waveguide .
For modes of a planar waveguide
![]() (6)
(6)
where ![]() is propagation constant
is propagation constant
![]() ,
,  ,
,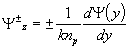 (7)
(7)
here index ![]() is
is ![]() for the field inside waveguiding layer and
for the field inside waveguiding layer and ![]() is
is ![]() outside layer
outside layer
![]() ,
, ![]() (8)
(8)
According to (3) functions ![]() and
and ![]() can be taken as
can be taken as
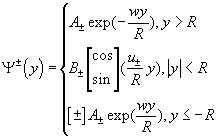 (9)
(9)
where
![]() ,
, ![]() (10)
(10)
for even ( symmetric ) and odd ( antisymmetric ) with ![]() ,
, ![]() and signs in
square brackets respectively .
and signs in
square brackets respectively .
Having put expressions (6) , (7) , (9) into (5) and having excluded coefficients ![]() and
and ![]() , we can obtain dispersion equations that give the relation between
propagation constant
, we can obtain dispersion equations that give the relation between
propagation constant ![]() and wave number
and wave number ![]() , wich is related to
, wich is related to ![]() according to (4) . For even modes this equation is
according to (4) . For even modes this equation is
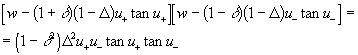 (11)
(11)
and for odd modes
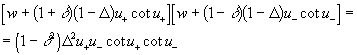 (12)
(12)
where we take in consideration (8) and
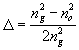 (13)
(13)
Because for optical waveguides
![]() (14)
(14)
right part the of equation that contains ![]() in (11) and (12) can be neglected , so it gives us the following equations
in (11) and (12) can be neglected , so it gives us the following equations
![]() (15)
(15)
![]()
where the equations with indexes ![]() and - are separated . It means that modes are divided into two classes ,
the first one is formed by planar waves with right-handed circular polarisation (described
by functions
and - are separated . It means that modes are divided into two classes ,
the first one is formed by planar waves with right-handed circular polarisation (described
by functions ![]() ) and the other is formed by
planar waves with left-handed circular polarisation (described by functions
) and the other is formed by
planar waves with left-handed circular polarisation (described by functions ![]() ) .
) .
Having introduced , as usual for the optical waveguides [5,6] , the normalised propagation constant and frequency
![]() ,
, ![]() (16)
(16)
where ![]() is related to
is related to![]() by expression
by expression
![]() (17)
(17)
so we will get
![]() ,
,  (18)
(18)
As far as according to (8) ![]() depends on
frequency , then
depends on
frequency , then
![]() ,
, 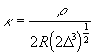 (19)
(19)
Including those expressions into (18) and then into equations (15) , than neglecting
small values ![]() and
and ![]() , with respect to 1 , but keeping their ratio
, with respect to 1 , but keeping their ratio ![]() , we receive the dispersion (eingenvalue)
equation
, we receive the dispersion (eingenvalue)
equation
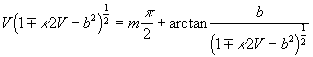 (20)
(20)
where ![]() is the number of a mode :
is the number of a mode : ![]() for even modes ,
for even modes , ![]() for odd modes . From (20) for
for odd modes . From (20) for ![]() we can derive an equation
we can derive an equation
![]() (21)
(21)
from which it is seen that a chiral waveguide in contrast to achiral has cut-off
frequencies both in lower and upper parts of friequency range . For the fundamental mode (![]() ) the frequency range where it exists is
determined by the relation
) the frequency range where it exists is
determined by the relation
![]() (22)
(22)
3. Asymmetrical planar waveguide
Asymmetrical planar waveguide is presented on Fig.2 , where ![]() is the refraction index of the substrate .
is the refraction index of the substrate .
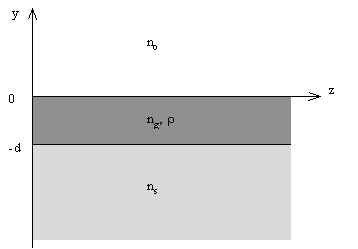
Fig.2. Asymmetrical planar waveguide .
The study of an asymmetrical waveguide is analogous to the case of a symmetrical waveguide . So we will give only the final result . The dispersion (eigenvalue) equation for modes of asymmetrical waveguide is
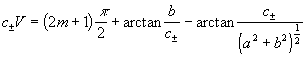 (23)
(23)
where
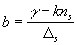 ,
, ![]() ,
, ![]()
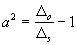 ,
, 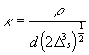 ,
, 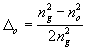 ,
, 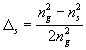 (24)
(24)
Because as usual ![]() ,
, ![]() , then
, then 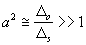 (25)
(25)
While ![]() we have an equation for cut-off
frequencies
we have an equation for cut-off
frequencies
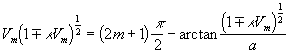 (26)
(26)
4. Dispersion characteristics
The dispersion dependencies ![]() for
symmetrical and asymmetrical chiral waveguide obtained by numerical solution of (20) and
(23) are shown on Fig. 3 and Fig. 4 . As we see the dispersion curves are divided into two
classes . One corresponds to the modes wich are described by function
for
symmetrical and asymmetrical chiral waveguide obtained by numerical solution of (20) and
(23) are shown on Fig. 3 and Fig. 4 . As we see the dispersion curves are divided into two
classes . One corresponds to the modes wich are described by function ![]() , the other one by
, the other one by ![]() . Every dispersion curve of the first class has cut-offs in lower
and upper parts of spectrum .This is a novel physical fact .
. Every dispersion curve of the first class has cut-offs in lower
and upper parts of spectrum .This is a novel physical fact .
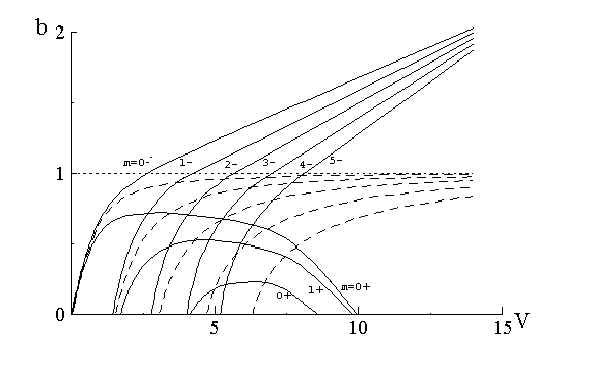
Fig.3. Mode dispersion characteristics for a symmetrical chiral waveguide for
. The dash lines stand for corresponding nonchiral waveguide .
Fig.4. Mode dispersion characteristics for an asymmetrical chiral waveguide for
,
,
. The dash lines stand for corresponding nonchiral waveguide .
It is shown in this paper that starting from a certain frequency ,chiral waveguides can guide modes of one polarisation in the multimode regime . They can be singlepolarising not only in singlemode regime as usual optical waveguides , but also in multimode operating regime .
These results were presented on International Workshop on Optical Waveguide Theory and Numerical Modelling, September 18-19, 1998, Hagen, Germany. Theory will be published in [7] completely with additional interesting details and interpretations.
References
Authors:
S.V. Demidov , K.V. Kushnarev ,
Victor Vasil'evich Shevchenko, e-mail: sto@mail.cplire.ru