| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 8 , 2000 |
ПОТЕНЦИАЛЬНАЯ ТОЧНОСТЬ РАДИОЛОКАЦИОННЫХ ИЗМЕРЕНИЙ ТОЛЩИНЫ СЛОИСТЫХ СРЕД
А.
Г. Оганесян, И. Б. Чайковский
Государственный
университет "Львовская политехника"
Получена 5 августа 2000 г.
Рассмотрены возможные оценки потенциальной точности измерения толщины слоистых сред и приведен сравнительный анализ с результатами имитационных и лётных испытаний радиолокационных станций проникающего (подповерхностного) зондирования.
В последние годы, после долгого перерыва, вновь возник интерес к проникающей (подповерхностной) радиолокации слоистых сред. Исследование возможностей РЛСПЗ (радиолокационных станций проникающего зондирования), применительно к измерению толщины льдов, начато чл. кор. АН СССР профессором В.В.Богородским (НИИ Арктики и Антарктики, С.-Петербург, Россия) в шестидесятых годах. Позже к работе подключились профессор М.И.Финкельштейн (Рижский институт инженеров Гражданской авиации – РИИГА, Рига, Латвия) и профессор А.Г.Оганесян (НИКИ ЭЛВИТ Государственного университета "Львiвська полiтехнiка", Львов, Украина). В лаборатории профессора М.И.Финкельштейна ещё 25 лет назад был создан первый самолётный измеритель толщины льда. В настоящее время РКИИГА закрыт, но лаборатория подповерхностного зондирования преобразована в независимую фирму "Радарные системы", которая создала целый ряд георадаров контактного типа (с её работами можно ознакомиться в Интернете: http://www.radsys.lv).
Времени прошло много, но до сих пор не рассмотрен вопрос о предельной точности измерения толщины слоя, например, дрейфующего морского льда. В большинстве случаев авторы ограничиваются демонстрацией картинок волновых полей отражённых сигналов.
Используем подход, предложенный Вудвордом [1] и применённый для оценки потенциальной точности радиовысотомеров [2] и систем ближней радиолокации [3]. Ограничимся однослойной средой, поскольку результат без труда обобщается на слоистую среду с произвольным количеством слоёв. Представим задачу измерения в дискретном виде. Для этого разобьём весь диапазон измеряемых толщин на
N интервалов. Обозначим интервал дискретизации где hmax и hmin – верхняя и нижняя границы диапазона измерения толщины слоя. Процедура измерения толщины сводится к определению номера интервала i, соответствующего толщине слоя hi=D h× i. Если априорная вероятность толщины hi равна p(hi), то величину полученной информации определяется как I[hi]=log2(1/p(hi))=-log2p(hi) (понятие меры информации было введено К. Шенноном). Ожидаемое, или среднее, значение этой информации, равно энтропии, которую записывают в виде бит]. (2)Энтропия максимальна, если априорное распределение
p(hi) равномерно. В этом случае p(hi)=1/N. Подставляя это значение в (2), получаем максимальное значение для энтропииЕсли измерение происходило без помех, то после него неопределённость исчезает, т. е. получается некоторое количество информации
I, равное величине энтропии, предшествующей измерению, т. е. I=H. Если же процессу измерения сопутствуют помехи, то после измерения энтропия полностью не исчезает, но убывает и при этом и при этом появляется некоторое количество информации I=H-Hx, где Hx - энтропия, оставшаяся после выполнения измерениягде
py(hi) - апостериорное распределение толщин.Необходимое для решения той или иной практической задачи количество информации
I должно быть получено в течение некоторого времени Tн (период наблюдения, время между двумя соседними измерениями (отсчётами) толщины слоя). Отсюда средняя скорость поступления информации [4]:или информационная способность. Для предельного случая равномерного априорного распределения и при апостериорном распределении вида сдвинутого импульса Кронекера
бит/с]. (6)Фундаментальное значение в теории информации имеют теоремы К.Шеннона, в которых он показал, что теоретический предел скорости передачи информации определяется пропускной способностью системы
бит/с], (7)где
Fc - полоса пропускания системы передачи информации, Pc и Pш – мощности соответственно сигнала и шумов в системе. В случае радиолокации Fc – эффективная ширина спектра принятого сигнала [1-4].Сравнивая (6) и (7) можно заметить следующее:
Если
R<C, то теоретически измерение возможно со сколь угодно малой погрешностью. Правда, для этого потребуется и неограниченно долгое время. При R>C измерение без погрешности невозможно принципиально.Очевидно, необходимо, чтобы выполнялось первое условие, поскольку в процессе преобразования принятого сигнала его объём уменьшается. Равенство
R=C возможно только в том случае, если в формуле (6) рассматривается сигнал на выходе, например, индикатора РЛСПЗ.Приравнивая (6) и (7), получаем
илигде
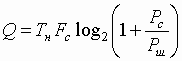 - объём сигнала.
- объём сигнала.
Формула (8) позволяет оценить абсолютную погрешность измерения (относительно измеряемого диапазона) по известному объёму сигнала. Для расчётов удобнее отношение сигнал/шум
D выразить в децибелах, время измерения как Тн=nTс, где Тс-длительность сигнала, а погрешность в процентах, тогдаОценки, даваемые теорией информации, справедливы асимптотически при беспредельном увеличении времени накопления, поэтому естественно возникает вопрос о достоверности таких оценок. Определённую сложность вызывает и оценка произведения
TнFc, поскольку сигнал не может одновременно быть ограниченным по длительности и ширине спектра. Марпл [5] рассматривает произведение эквивалентных величин TеFе:где Т – интервал дискретизации сигнала х(
t). Таким образом, эквивалентная длительность дискретизированного сигналаопределяется как "площадь"
этого сигнала, поделённая на его
центральное значение. Эквивалентная ширина
спектра определяется аналогично. При этом
для действительных симметричных сигналов с
максимальным значением в начале координат TеFе=1.
Для расширения класса сигналов используют
эквивалентные среднеквадратичные
длительность сигнала и ширину его спектра
[5], при
этом ![]() .
.
Кривая 2 на рис. 1 построена по формуле
(9) в предположении, что TеFе= TнFс=1. Аналогичная зависимость получена на цифровой имитационной (для желающих ознакомиться с имитационной моделью сообщаем свой адрес электронной почты: oganes@polynet.lviv.ua) модели корреляционной РЛСПЗ [6] при N=32 (кривая 3). Вычислялась среднеквадратичная погрешностьВеличина относительной погрешности (11) при малых средних значениях модуля
ho может быть весьма большой, что вызывает неудобства при вычислении и интерпретации результата. Лучше согласуется с информационной трактовкой процесса измерения и не вызывает проблем деления на нуль, если оценивать погрешность относительно величины измеряемого диапазона: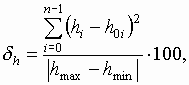 %.
%.
Поделив числитель и знаменатель этой формулы на цену единицы D , получим более удобную формулу
где D
i= ki-koi – разность между относительными значениями измеренной и истинной величин.Результат
получился довольно странный (см. рис.1): на большей части диапазона сигнал/шум погрешность оказалась меньше (кривая 3), чем теоретический предел, определяемый формулой (9) (кривая 2), справедливой при условии, что измеряемые величины равновероятны, а шум белый, нормальный. Эти же условия приняты и в имитационной модели.Иной результат получается, если принять во внимание, что дискретизированный сигнал длительностью
NT имеет бесконечный спектр с расстоянием между спектральными линиями 1/NT и периодом 1/Т. Поскольку один период полностью определяет весь спектр независимо от формы сигнала, примемДля этого случая построена кривая 1 (рис.1), которая значительно лучше согласуется с имитационными данными. Однако при малых отношениях сигнал/шум расхождения остаются и их нельзя отнести за счёт недостаточного объёма статистических испытаний. Дело в том, что формулы (6, 7) и полученная из них формула (9), не учитывают случайных совпадений истинной и измеренной величин (и испорченные часы
дважды в сутки показывают совершенно правильное время).Рис. 1. Зависимость погрешностей от отношения сигнал / шум.
Fc=32;1 – Теоретическая кривая, построенная по формуле (9) для Тн
Для оценки этого рассмотрим распределение вероятностей разности двух случайных последовательностей D
=h-ho. На рис. 2 показано распределение вероятностей p(D h) при r=0, т. е. когда последовательности h и ho независимы. Первая последовательность h формировалась датчиком случайных чисел, а вторая ho определялась на основе теоремы Винера-Колмогорова:![]()
![]()
(использован оператор Mathcad 6.0 Plus)
где
runif(300,0,32) – датчик 300 равновероятных случайных чисел в интервале 0…31, r – коэффициент корреляции между последовательностями. При r=0 оценка погрешностей по формулам (11) и (12) соответственно равна 81% или 41%, а не 100%, как следует из формулы (9). Кстати, на рис. 2 видно, что наиболее вероятное значение погрешности (мода) в этом случае равно нулю. Если r=1, т. е. когда h=ho, погрешность измерения равна нулю.Естественно, удобнее иметь оценку погрешности, которая для некоррелированных последовательностей равнялась бы 100
%, а не произвольному значению, кстати, зависящему от распределения вероятностей измеряемых величин. Такой оценкой может быть скорректированное значение среднеквадратичной погрешности d , зависящее от коэффициента взаимной корреляции R между измеренными и истинными значениями последовательностейгде a
- константа, величина которой выбирается произвольно, но так, чтобы, начиная с некоторого значения, влиянием коэффициента корреляции можно было бы пренебречь, т. е.Рис. 2. Распределение вероятностей абсолютных погрешностей
На рис. 3 показаны коэффициенты корреляции
R, полученные при имитационных испытаниях РЛСПЗ двух типов, а на рис. 1 показана кривая 4, которая получена путём коррекции кривой 3 по формуле (14) при a =500. Хорошо видно, что начиная с отношения сигнал/шум=-5 дБ, обе кривые практически совпадают. Теперь кривая 4 во всём диапазоне проходит выше кривой 1. Погрешность импульсной РЛСПЗ [6] представлена кривой 6.Рис. 3. Коэффициенты взаимной корреляции между истинными и измеренными значениями.
1 –
Корреляционная РЛСПЗ; 2 –импульсная РЛСПЗ.
Рассмотрим ещё одну оценку – неравенство Крамера-Рао, позволяющее определить нижнюю границу дисперсии несмещённой оценки скалярного параметра a по случайной последовательности
x: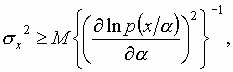
где
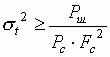
при оценке погрешности запаздывания отражённого сигнала независимо от используемого метода
[7]. Перейдём к относительным единицам:Эта граница погрешности показана на рис. 1 (кривая 7). На этом же рисунке показаны области погрешностей (эллипсы К и И), полученные во время лётных испытаний РЛСПЗ над дрейфующими льдами Арктического бассейна.
При отношениях сигнал/шум ниже –5 дБ, предельные значения погрешностей мало отличаются от соответствующих погрешностей, полученных при имитационных испытаниях. В рабочем же диапазоне РЛСПЗ, начиная с 10 дБ и выше, предельные значения погрешностей отличаются значительно, на несколько порядков, хотя результаты имитационных и натурных испытаний совпадают достаточно хорошо. Причина несоответствия в том, что формулы (9) и (15), по которым вычислялись предельные значения погрешностей, не учитывают дискретного характера измерительного устройства. Квантование измеряемой величины приводит к появлению погрешности, зависящей только от количества уровней квантования
N и равной [4]:которая при
N=32 равна примерно 1 %, как показано на рис. 4 (обозначения такие же, как и на рис. 1).Рис. 4. Зависимость погрешностей с учётом квантования (обозначения как и на рис. 1)
Таким образом,
Литература
Авторы:
Альберт Георгиевич ОГАНЕСЯНИгорь Борисович
ЧАЙКОВСКИЙ
Государственный университет "Львовская
политехника"
Ведущий инженер, аспирант.