| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 7, 2001 |  |
ОПТИМИЗАЦИЯ ПОСЛЕДОВАТЕЛЬНОГО И ДИХОТОМИЧЕСКОГО ПОИСКОВЫХ АЛГОРИТМОВ МЕТОДОМ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
А. Г. Филатов
Воронежский Научно-исследовательский Институт Связи
Получена 17 мая 2001 г.
Проведена оптимизация последовательной и дихотомической поисковых процедур методом динамического программирования с целью получения их потенциальных характеристик. Показано, что наибольший эффект достигается при оптимизации дихотомии. Проведен сравнительный анализ двух поисковых алгоритмов, применительно к поиску сигнала в частотном диапазоне, в ходе которого показано, что, начиная с некоторого, весьма низкого отношения сигнал/шум, дихотомия имеет выигрыш.
Введение
Большинство современных радиотехнических систем (РТС), включает процедуру оценивания параметров сигналов. Примером может служить определение частоты сигнала в системах с псевдослучайной перестройкой рабочей частоты (ППРЧ), определение задержки отраженного сигнала в системах радиолокации и навигации, синхронизация в цифровых системах связи и т.д.
Одним из методов оценки параметров является поиск. При поиске осуществляют пошаговый просмотр области неопределенности с помощью одноканального устройства (или устройства с приемлемым числом каналов). Канал оценки в данном случае представляет собой вычислитель функции правдоподобия и устройство вынесения решения по вычисленному значению. При этом на каждом шаге снижается неопределенность оцениваемого параметра. Существует две различные стратегии или вида поиска - последовательный и полихотомический. Все остальные алгоритмы, так или иначе, являются совокупностью этих двух.
При последовательном поиске область неопределенности разбивается на ячейки, величина которых определяется требованиями к точности определения параметра искомого сигнала (объекта). Затем выполняется последовательная проверка гипотез о наличии объекта поиска в одной из ячеек области неопределенности. По завершении проверки гипотезы выносится решение относительно двух альтернатив: значение параметра соответствует проверяемой гипотезе или нет, и во втором случае осуществляется переход к следующей гипотезе и т.д. Проверка простой гипотезы называется шагом поиска. В связи с тем, что решение на каждом шаге выносится относительно именно двух альтернатив, поиск получил название двоичного [1].
Полихотомический алгоритм представляет собой параллельный просмотр нескольких частей области неопределенности с последующим вынесением решения о присутствии объекта поиска в одной из них. На следующем шаге выполняется разбиение определенной на предыдущем шаге части области неопределенности и т.д. Поиск выполняется до тех пор, пока разбиение не приведет к требуемой точности искомого параметра. Другими словами, от шага к шагу поиска выполняется сужение области неопределенности. Частным и наиболее простым случаем полихотомии является дихотомическая поисковая процедура, где разбиение области выполняется на две части. Дихотомический поисковый алгоритм также относится к двоичным поисковым процедурам.
Обе описанные поисковые
процедуры могут быть однопроходными или циклическими. Однопроходные поисковые
процедуры предусматривают проведение поиска без повторных циклов сканирования
области неопределенности, в то время как циклические допускают возвращение к
предыдущим шагам поиска. Однопроходные процедуры характеризуются двумя
параметрами: вероятностью успешного завершения Q и средним временем
поиска Тср. Причем в [2] показано, что задачи
максимизации вероятности Q
при фиксированном времени Тср и минимизации Тср при
фиксированном Q
имеют общее решение, т.е. обе задачи приводят к одной и той же оптимальной
совокупности времен анализа на каждом шаге поиска
![]() и порогов обнаружения Vi
(в случае поиска с двухпороговым решающим устройством Вальда порогов V0i
и V1i
). Для решения задачи максимизации вероятности успеха Q
при фиксированном среднем времени применим метод динамического программирования.
и порогов обнаружения Vi
(в случае поиска с двухпороговым решающим устройством Вальда порогов V0i
и V1i
). Для решения задачи максимизации вероятности успеха Q
при фиксированном среднем времени применим метод динамического программирования.
Основной задачей данной работы является исследованию подходов к оптимизации последовательного и дихотомического поиска методом динамического программирования. Целью оптимизации является нахождение потенциальных характеристик данных процедур и их сравнительный анализ. Оптимизация проведена на примере поиска сигнала имеющего постоянную огибающую (ФМ или ЧМ сигнал) с шириной спектра Df0 в частотном диапазоне АDf0, в допущении что поиск проводится с помощью однопорогового обнаружителя без памяти, т.е. входной сигнал не может быть записан и для каждого нового шага поиска требуется его новая реализация.
1. Оптимизация последовательного поиска
Прямое использование метода динамического программирования предполагает одновременную оптимизацию времени анализа ячейки области неопределенности и порога обнаружения. Представим процедуру последовательного поиска в виде древовидного графа, вершиной которого является узел, соответствующий первому измерению (см. рис.1).
Рис. 1. Дерево однопроходного последовательного поиска.
Вероятность успешного завершения поиска из узла А-1 равна
где
![]() -
время анализа i-й
ячейки области неопределенности, Vi
– порог обнаружения,
-
время анализа i-й
ячейки области неопределенности, Vi
– порог обнаружения, ![]() - апостериорная вероятность присутствия
сигнала в А-1 ячейке области неопределенности. Если предположить, что сигнал
равновероятно может находиться в любой из ячеек и на i-1
предыдущих шагах не было пропуска сигнала, то вероятность присутствия сигнала
при анализе i-й
ячейки равна
- апостериорная вероятность присутствия
сигнала в А-1 ячейке области неопределенности. Если предположить, что сигнал
равновероятно может находиться в любой из ячеек и на i-1
предыдущих шагах не было пропуска сигнала, то вероятность присутствия сигнала
при анализе i-й
ячейки равна
Данное значение является верхней границей вероятности p(xi) при осуществлении поиска. Нижней границей является ноль - случай пропуска сигнала на предыдущих шагах.
В общем случае вероятность успешного поиска из i-го узла равна
где Ti - время, выделенное на поиск из i-го узла. Времена Ti , Ti+1 и ti связаны следующим выражением
Оптимизация
методом динамического программирования заключается в том, что для каждого узла
дерева поиска, начиная с последнего, рассчитывается вероятность успешного
завершения поиска для возможных пар величин
![]() и
и
![]() , причем расчет выполняется
следующим образом
, причем расчет выполняется
следующим образом
Вероятности присутствия сигнала на текущем и предыдущем шагах поиска связаны выражением
где
![]() - вероятность того, что при
вынесении решения "сигнала нет" его действительно нет, равная
- вероятность того, что при
вынесении решения "сигнала нет" его действительно нет, равная
В теории динамического
программирования [3] выражение (5)
называется функцией Беллмана. Таким образом, функция Беллмана, рассчитанная для
первого узла от аргументов T1=TСР
и
![]() ,
есть максимально достижимая вероятность успешного поиска при заданном времени
поиска TСР.
Повторный проход по дереву поиска, но
уже от первого узла к последнему, позволяет восстановить значения порогов
времен анализа
,
есть максимально достижимая вероятность успешного поиска при заданном времени
поиска TСР.
Повторный проход по дереву поиска, но
уже от первого узла к последнему, позволяет восстановить значения порогов
времен анализа
![]() и Vi,
приведших к найденной вероятности успеха.
и Vi,
приведших к найденной вероятности успеха.
Рассмотренный метод
представляет собой двумерную оптимизацию и весьма трудоемок. Гораздо более
приемлемым вариантом является одномерная оптимизация, когда в начале задаются
определенными значениями
![]() , например фиксированными
, например фиксированными
![]() , и затем
оптимизируют пороги обнаружения Vi,
таким образом, чтобы достичь максимальной вероятности успеха. Среднее время
поиска в таком случае можно вычислить с помощью следующего выражения
, и затем
оптимизируют пороги обнаружения Vi,
таким образом, чтобы достичь максимальной вероятности успеха. Среднее время
поиска в таком случае можно вычислить с помощью следующего выражения
где рi – вероятность того, что поиск дойдет до i-го шага поиска, получаемая рекуррентным образом, начиная с шага номер один.
Рассмотрим
случай, когда время анализа на всех шагах поиска одинаково, т.е.
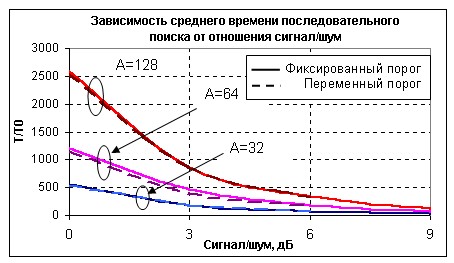
![]() . На рис.2
представлены зависимости среднего времени последовательного поиска,
оптимизированного методом динамического программирования, от отношения
сигнал/шум для А=32-128 и вероятностей успеха Q=0,9. Предполагается,
что искомый сигнал имеет постоянную огибающую, а время поиска представлено
относительно интервала времени T0=1/Df0.
На том же рисунке приведены зависимости среднего времени поиска для случая,
когда при проверке частотных каналов порог и время анализа были фиксированными.
. На рис.2
представлены зависимости среднего времени последовательного поиска,
оптимизированного методом динамического программирования, от отношения
сигнал/шум для А=32-128 и вероятностей успеха Q=0,9. Предполагается,
что искомый сигнал имеет постоянную огибающую, а время поиска представлено
относительно интервала времени T0=1/Df0.
На том же рисунке приведены зависимости среднего времени поиска для случая,
когда при проверке частотных каналов порог и время анализа были фиксированными.
Рис. 2. Сравнение последовательной поисковой
процедуры с фиксированным и переменным порогом
Среднее время поиска всегда ниже при перестраиваемом пороге, и также вероятность успешного поиска Q всегда несколько лучше, однако выигрыш не является существенным.
Был также рассмотрен
случай, когда время анализа
![]() линейно нарастает, т.е. имеет место
линейная зависимость времени анализа от номера проверяемой частотной ячейки. К
оптимизируемым параметрам в данном случае был добавлен наклон прямой
линейно нарастает, т.е. имеет место
линейная зависимость времени анализа от номера проверяемой частотной ячейки. К
оптимизируемым параметрам в данном случае был добавлен наклон прямой
![]() . Однако и
здесь выигрыша составляет единицы процентов.
. Однако и
здесь выигрыша составляет единицы процентов.
В результате можно
сказать, что метод динамического программирования, приводящий к переменным от
шага к шагу поиска порогам обнаружения Vi
и времени накопления
![]() , незначительно выигрывает у метода
оптимизации, который предполагает данные параметры фиксированными. В то же
время сложность оптимизации при последнем подходе ниже.
, незначительно выигрывает у метода
оптимизации, который предполагает данные параметры фиксированными. В то же
время сложность оптимизации при последнем подходе ниже.
2. Оптимизация дихотомического поиска
Рис. 3. Дерево дихотомического поиска
Однопроходный
дихотомический поиск узкополосного сигнала в частотном диапазоне предполагает
выполнение N=log2A
шагов, где на первом шаге весь анализируемый частотный диапазон разбивается на
две части и определяется, в какой половине находится искомый сигнал. На втором
шаге делится пополам поддиапазон, найденный на предыдущем шаге и т.д. В
результате на последнем шаге выбор осуществляется между поддиапазонами,
содержащими по одной ячейке. Финальная вероятность успешного поиска Q
в данном случае будет равна произведению вероятностей вынесения правильного
решения на каждом шаге Qi,
где i=1,N.
Если задано некоторое время Тср, в течение которого необходимо
провести поиск, то одним из вариантов распределения имеющегося общего времени
между шагами является такой, при котором вероятности вынесения правильного
решения на каждом шаге будут равны, т.е.
![]() . Назовем этот подход первым.
. Назовем этот подход первым.
Однако от шага к шагу
поиска ширина анализируемого частотного поддиапазона изменяется и,
следовательно, изменяется отношение сигнал/шум по входу решающего устройства,
выносящего решение в пользу одного или другого поддиапазона. Поэтому оправдано
предположить, что выбор вероятностей
![]() неоптимален. Проведем оптимизацию
распределения времени дихотомического поиска сигнала между шагами методом
динамического программирования и назовем этот подход вторым.
неоптимален. Проведем оптимизацию
распределения времени дихотомического поиска сигнала между шагами методом
динамического программирования и назовем этот подход вторым.
Предположим, что искомый сигнал имеет постоянную огибающую и время анализа на шаге поиска T>>1/Df0 и при этом поиск осуществляется с помощью двух фильтров с перестраиваемыми полосой и центральной частотой. Вычисляется разность выходных сигналов фильтров, детектирование и некогерентное накопление. Решение в пользу одного либо другого поддиапазона выносится с помощью решающего устройства (РУ), сравнивающего полученную величину с нулевым порогом. В таком случае вероятность вынесения правильного решения с помощью однопорогового РУ на i-м шаге поиска равна
где
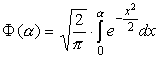 - функция Крампа;
- функция Крампа;
![]() - отношение
сигнал/шум по входу РУ на i-м
шаге поиска в отсутствии накопления, зависящее от номера шага поиска и
отношения сигнал/шум в элементарной ячейке
- отношение
сигнал/шум по входу РУ на i-м
шаге поиска в отсутствии накопления, зависящее от номера шага поиска и
отношения сигнал/шум в элементарной ячейке
![]() ;
;
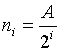 - число накапливаемых отсчетов
на интервале времени 1/Df0,
зависящее от номера шага дихотомического поиска; Т - время анализа на шаге
поиска, представленное относительно интервала 1/Df0.
Следует отметить, что в зависимости от номера шага поиска на интервале времени
1/Df0
может быть разное число накапливаемых отсчетов n, поскольку на разных
шагах анализируются частотные поддиапазоны разной ширины.
- число накапливаемых отсчетов
на интервале времени 1/Df0,
зависящее от номера шага дихотомического поиска; Т - время анализа на шаге
поиска, представленное относительно интервала 1/Df0.
Следует отметить, что в зависимости от номера шага поиска на интервале времени
1/Df0
может быть разное число накапливаемых отсчетов n, поскольку на разных
шагах анализируются частотные поддиапазоны разной ширины.
Если
на поиск из узла, находящегося на последнем уровне, выделено время t
и предыдущие шаги были безошибочными, то вероятность правильного завершения
поиска
![]() равна
равна
Та же вероятность для предпоследнего уровня равна
где
![]() –
время отводимое на (N-1)-й
шаг, а
–
время отводимое на (N-1)-й
шаг, а
![]() -
на следующий.
-
на следующий.
В общем случае для i-го шага имеем
Оптимизация методом
динамического программирования заключается в том, что для каждого уровня дерева
поиска, начиная с последнего, рассчитывается вероятность успешного завершения
поиска
![]() для
всех возможных значений
для
всех возможных значений
![]() , причем расчет выполняется следующим
образом
, причем расчет выполняется следующим
образом
Выражение (13) представляет собой функцию Беллмана и ее значение, рассчитанное для первого шага от аргумента Тср, есть максимально достижимая вероятность успеха при заданном времени поиска Тср. Повторный проход по дереву поиска, но уже от первого уровня к последнему, позволяет восстановить значения времен анализа Ti, приведших к найденной вероятности успеха. Исходя из известных Ti можно определить вероятности правильного решения на каждом из шагов поиска Qi .
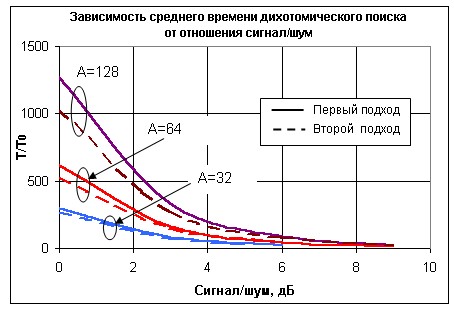
На
Рис.
4
представлены зависимости времени поиска сигнала в частотном диапазоне при
![]() (первый подход)
и поиска, оптимизированного методом динамического программирования (второй подход).
(первый подход)
и поиска, оптимизированного методом динамического программирования (второй подход).
Рис. 4. Сравнение двух подходов к построению дихотомического поиска
Как следует из рисунка, метод динамического программирования позволяет лучшим образом распределить общее время поиска между шагами. При этом распределение времени приводит к тому, что на первых шагах вероятность правильного решения ниже, чем на последних. В результате наблюдается выигрыш перед первым подходом, причем выигрыш растет с ростом величины частотного диапазона А и со снижением отношения сигнал/шум.
3. Сравнение последовательного и дихотомического поисковых алгоритмов
Полученные выше характеристики последовательного и дихотомического поисковых алгоритмов являются потенциальными, в связи с чем интересным является проведение их сравнительного анализа.
Сначала определим верхнюю и нижнюю границы отношения средних времен поиска. При большом отношении сигнал/шум для вынесения решения на шаге поиска, независимо от поискового алгоритма, требуется один отсчет. При последовательном поиске максимальное число шагов равно A-1 и при равновероятном нахождении сигнала в пределах частотного диапазона среднее число шагов равно (A-1)/2, а минимальное среднее время поиска равно
При дихотомии среднее время равно
В результате деления (14) на (15) получается R=A/4. Таким образом, предельный выигрыш дихотомии пропорционален величине области неопределенности А.
Анализ поведения кривых рис.2 и рис.4 в области низких отношений сигнал/шум h02, представленных в логарифмическом масштабе, дает основания аппроксимировать их следующими функциями:
где отношение сигнал/шум h02 выражено в децибелах, а KА – коэффициент определяемый величиной области неопределенности А. Так для последовательного поиска при Q=0.9 и А=32;64;128 коэффициент KА =2,678; 3,01; 3,346 соответственно. Для дихотомии KА =2,39; 2,704; 3,01. Исходя из выражений (16), (17) можно определить величину h02, ниже которой последовательный поиск будет быстрее дихотомического:
Для А=32;64;128 данная величина равна соответственно h02= -18; -19.1; -21 дБ.
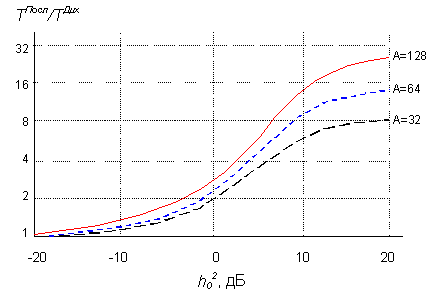
На рис.5 представлены зависимости отношения средних времен последовательного и дихотомического поиска. Из рисунка следует, что, начиная с весьма низкого отношения сигнал/шум, дихотомический поиск выигрывает.
Рис. 5. Отношение средних времен последовательного и дихотомического поиска
Заключение
В ходе работы была проведена адаптация метода динамического программирования к оптимизации последовательного и дихотомического алгоритмов поиска с целью нахождения их потенциальных характеристик. Поведена классификация параметров поисковых алгоритмов в результате которой число оптимизируемых параметров было ограничено, что привело к существенному упрощению оптимизации. Показано, что наибольший по времени поиска выигрыш динамическое программирование дает при оптимизации дихотомии.
Проведенное сравнение потенциальных характеристик последовательного поиска и дихотомии применительно к поиску сигнала в частотном диапазоне показало, что, начиная с некоторого, весьма низкого, отношения сигнал/шум, дихотомия выигрывает по среднему времени поиска.
Литература
1. Каневский З.М., Литвиненко В.П. Теория скрытности. – Воронеж: Изд-во ВГУ, 1991. – 144с.
2. Василенко О.О. Автореферат диссертационной работы "Оптимизация поиска сигналов связи и управления в задачах анализа скрытности". Воронеж, ВГТУ 1999.
3. Беллман Р. Процессы регулирования адаптацией. М., 1964.
Автор:
Филатов Анатолий Геннадьевич, е-mail: filatov@kodofon.vrn.ru,
Воронежский Научно-исследовательский Институт Связи

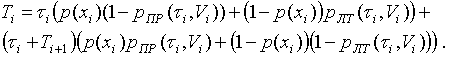
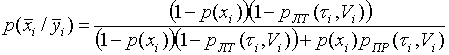 .
. 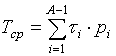 ,
, 

 ,
, 
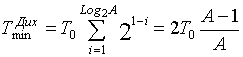 .
.  . ( 18 )
. ( 18 )