| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 9, 2001 |  |
ФАКТОРЫ, ВЛИЯЮЩИЕ НА РАСПРОСТРАНЕНИЕ ММ ВОЛН В ПРИЗЕМНОМ СЛОЕ АТМОСФЕРЫ
Г. К. Загорин, А. Ю. Зражевский, Е. В. Коньков, А. В. Соколов, С. В. Титов, Г. И. Хохлов, Л. Ф. Черная
Институт радиотехники и электроники РАН
Получена 3 августа 2001 г.
Приведены результаты теоретических и экспериментальных исследований влияния: молекулярного поглощения в атмосферных газах; спектральных и поляризационных особенностей рассеяния и ослабления радиоволн в гидрометеорах; вертикальной рефракции; турбулентности воздуха и отражения подстилающей поверхностью на распространение миллиметровых волн.
Введение
Понимание особенностей взаимодействия волн ММ диапазона с молекулами атмосферных газов, с гидрометеорами, с турбулентными неоднородностями воздуха, а также оценка влияния на характеристики принимаемых сигналов вертикальной стратификации атмосферы и отражений от подстилающей поверхности являются весьма важными во многих практических приложениях. В работе приведены результаты теоретических и экспериментальных исследований, выполненных в ИРЭ РАН в последние годы по этим направлениям [1-3].
Проблема описания микроволнового поглощения в газах интересует радиофизиков как в России, так и за рубежом более полувека. Однако, несмотря на значительные усилия специалистов по теоретическому описанию спектров полярных газов, до сих пор не удавалось создать теорию, адекватную измеряемым величинам поглощения. Из-за сложности способов учета межмолекулярных взаимодействий до сих пор еще не получены аналитические выражения для спектров поглощения воздуха в широком диапазоне частот, а также давлений и температур.
В ИРЭ РАН был предложен и развит новый подход к описанию молекулярного поглощения. Оказалось, что результаты теоретических расчетов на основе метода функций памяти и моделей обобщенной вращательной диффузии хорошо согласуются с экспериментом без привлечения других гипотез (например, димерного механизма поглощения). Этот подход позволил лучше понять механизм взаимодействия электромагнитных волн с молекулами паров воды и кислорода [4,5].
В окнах прозрачности атмосферы на приземных линиях связи миллиметровые волны (ММВ) наибольшее ослабление испытывают в осадках. Вызвано это двумя причинами: во-первых, тем, что характерные размеры капель того же порядка, что и длина волны излучения, из-за чего дифракционное рассеяние каплями носит резонансный характер; во-вторых, тем, что большие значения мнимой части комплексного показателя преломления воды, обусловливают высокий уровень поглощения энергии волны в объеме капли. Следует отметить, что весьма основательно экспериментально и теоретически изучено ослабление радиоволн в осадках, установлены его спектральные и температурные зависимости, а также статистические характеристики; заметно хуже исследовано рассеяние радиоволн в осадках.
Влияние рассеяния ММВ в осадках на работу приземных линий связи может быть крайне неблагоприятным, так как оно приводит к ухудшению условий электромагнитной совместимости линий связи между собой и с другими радиоэлектронными системами, уменьшает скрытность передачи информации, создает электромагнитные помехи различным службам, нарушает экологию окружающей среды.
Предпринятые нами теоретические исследования эффектов рассеяния радиоволн в осадках (в том числе и многократного) базируются на реализации строгого решения задачи дифракции плоской электромагнитной волны на однородном диэлектрическом шаре (теория Ми) и на численном решении краевой задачи для системы интегро-диференциальных уравнений теории переноса поляризованного излучения в осадках.
Вертикальная неоднородность атмосферы может приводить к искривлению траекторий распространения (рефракции), к смещению центра пучка, и соответствующему изменению уровня сигнала, к многолучевому и волноводному распространениям или даже к отсутствию связи между пунктами. Для определения рефракции в сферически-слоистой атмосфере был разработан алгоритм, позволяющий при любых вертикальных профилях коэффициента преломления находить траектории радиоволн по координатам источника и приемника. С помощью этого алгоритма по метеопараметрам, измеренным Институтом экспериментальной метеорологии (ИЭМ) на высотах от 0 до 300 м в течение года, исследована статистика траекторных параметров на различных трассах приземного слоя атмосферы (ПСА).
Для оценки влияния турбулентности воздуха на параметры волны решена задача нахождения статистических характеристик флуктуаций амплитуды, фазы и угла прихода гауссова пучка ММВ в слабопоглощающей турбулентной среде. Получены асимптотические выражения для среднего квадрата флуктуаций уровня амплитуды, флуктуаций угла прихода и корреляционной функции флуктуаций амплитуды. Исследовано влияние усредняющего действия приемной апертуры на интенсивность флуктуаций амплитуды.
Из-за влияния подстилающей
поверхности ПСА чрезвычайно изменчив в пространстве и времени и является самым
сложным для изучения слоем атмосферы. До сих пор для поля показателя
преломления в ПСА не существует достаточно надежной и универсальной
математической модели, позволяющей в любых ситуациях рассчитывать параметры,
распространяющихся в нем ММВ. Вариации амплитуды и угла прихода миллиметровых
волн (![]() =3,3 мм),
обусловленные турбулентностью и стратификацией приземного слоя атмосферы,
экспериментально исследовались на трассе длиной 14 км совместно с МГТУ им. Баумана.
В течение двух лет изучались статистические характеристики вертикальной и
горизонтальной составляющих угла прихода и их временные спектры в диапазоне 10-5
–10 Гц.
=3,3 мм),
обусловленные турбулентностью и стратификацией приземного слоя атмосферы,
экспериментально исследовались на трассе длиной 14 км совместно с МГТУ им. Баумана.
В течение двух лет изучались статистические характеристики вертикальной и
горизонтальной составляющих угла прихода и их временные спектры в диапазоне 10-5
–10 Гц.
При функционировании атмосферных радиоканалов систем передачи информации при небольших (~ 10 - 15 м) высотах корреспондирующих пунктов (малые углы скольжения) на вход приемной антенны из-за многолучевости могут поступать как прямые, так и отраженные подстилающей поверхностью сигналы, что вызывает различные интерференционные эффекты и приводит к существенным ограничениям ширины полосы. Проведены эксперименты по выявлению интерференционной структуры поля ММВ и получена оценка полосы пропускания радиоканала в условиях влияния подстилающей поверхности.
Ниже результаты этих исследований подробно изложены по разделам.
1. Молекулярное поглощение
При вычислении молекулярных спектров поглощения газовых компонент атмосферы в силу сложности теории приходится использовать многочисленные аппроксимации, влияющие на точность конечного результата или приводящие к асимптотическим зависимостям для отдельных областей спектра, отдельных линий и даже частей линий (крыла, периферии, центра). Существенным моментом в теоретическом анализе частотных зависимостей спектров поглощения полярных газов является вопрос о расхождении экспериментальных данных с результатами теоретических расчетов (например, в случае кислорода при больших давлениях, водяного пара), основанных на трактовках соударений, известных как приближения Лорентца, Ван Флека-Вейскопфа, Гросса и некоторых других [6-10]. В этих трактовках столкновительного уширения решение задачи об определении поглощения сводится к рассмотрению двухуровневой системы, обуславливающей отдельные спектральные линии. В результате спектр поглощения представляет собой совокупность вкладов от изолированных переходов. Для объяснения указанных расхождений теории с экспериментом вводят предположения о характере межмолекулярных взаимодействий (столкновений), требующие рассмотрения многоуровневых систем, и подчеркивается важность учета возникающих в таких системах эффектов интерференции линий. Выдвигаются также гипотезы о дополнительных механизмах молекулярного поглощения. При этом иногда возникает ряд противоречий в качественной трактовке расхождений теории с экспериментом [11-14].
В свете изложенного теоретически изучено распространение ММ и СБММ радиоволн в полярных атмосферных газах (кислороде, водяном паре) [1-12, 15]. Основные задачи исследования заключались в следующем:
- в разработке удобной для практических приложений методики численного расчета спектров поглощения полярных газов на основе метода функций памяти и моделей обобщенной вращательной диффузии, учитывающих интерференцию линий поглощения [15, 17-23];
- в изучении и объяснении на основе данной методики аномальных особенностей спектров поглощения полярных газов [1, 9-12, 16, 21];
- в создании модели молекулярного поглощения кислородом (квантового аналога модели J-диффузии) для объяснения особенностей его спин-вращательного спектра в широком диапазоне давлений [5, 7, 10];
- в изучении влияния интерференционных эффектов на спектры поглощения газов [1];
- в создании новой модели молекулярного поглощения, предназначенной для объяснения аномалий поглощения радиоволн в окнах прозрачности атмосферы и учитывающей конечную длительность соударений [2, 22, 24-28].
В результате теоретических и экспериментальных работ был развит метод функций памяти применительно к описанию на молекулярном уровне комплексной диэлектрической проницаемости полярных газов для молекул произвольной симметрии. Оказалось, что предложенный метод может использоваться в качестве эффективного инструмента в изучении особенностей распространения радиоволн в полярных газах [1, 3]. Существенными результатами развитой теории являются:
- учет различия в значениях полуширин линий в спектрах поглощения газов [21];
- вычисление в аналитическом виде функций памяти ряда квантовых аналогов моделей обобщенной вращательной диффузии [1, 8];
- учет конечной длительности столкновений молекул [2, 22].
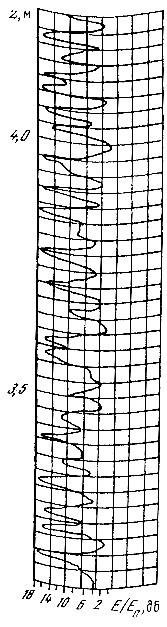
Было также установлено, что предложенная модель молекулярного поглощения в газах (квантовый аналог модели J-диффузии) адекватно описывает спин-вращательный спектр кислорода в широком диапазоне давлений (0,1-60 атм.) (см. рис.1, 2), а также растворов с газоподобными спектрами (рис.3) [5, 7, 10, 24-29].
Рис.1.
Отнесенный к давлению тангенс потерь ![]() молекулярного
кислорода как функция давления P на частоте n=0,3023 см-1,
рассчитанный для моделей J-диффузии (сплошная линия) и Ван Флека-Вайскопфа
(штриховая линия); квадратики - экспериментальные данные.
молекулярного
кислорода как функция давления P на частоте n=0,3023 см-1,
рассчитанный для моделей J-диффузии (сплошная линия) и Ван Флека-Вайскопфа
(штриховая линия); квадратики - экспериментальные данные.
Рис.2. Спектр поглощения кислорода в сухой атмосфере в диапазоне частот 54-66 ГГц при 29,7 оС. Сплошные линии - расчет в рамках модели J-диффузии, кружочки - экспериментальные данные. Кривые 1-6 соответствуют давлениям - кПа (высотам - км) 101,3 (0), 70,11 (3), 47,19 (6), 30,81 (9), 19,49 (12), 12,1 (15).
Рис.3. Нормированные спектры коэффициента поглощения растворов H2O (штриховая линия) и D2O (сплошная линия) в C6H6 для J-диффузии с конечной длительностью столкновений. Эксперимент для H2O (¨¨) и D2O (··) - из работы [24].
Кроме того предложена модель, учитывающая конечную длительность столкновений молекул и практически полностью соответствующая экспериментальным данным по поглощению ММ и СБММ радиоволн в окнах прозрачности атмосферных паров воды [2, 6, 9, 12, 16].
Как метод функций памяти, так и модели обобщенной вращательной диффузии нашли применение в теории диэлектрической релаксации [24-28], позволив добиться существенно лучшего согласия теории с экспериментом.
2. Особенности распространения миллиметровых волн в дожде
Как известно, максимум
ослабления радиоволн в дождях наблюдается в ММ диапазоне волн. Ослабление
обусловлено двумя механизмами: поглощением энергии волны в объеме капли дождя и
дифракционным рассеянием излучения каплей во внешнее пространство. При этом,
как отмечалось в работах [30-32], вклад в ослабление вносит лишь рассеяние в
направлении вперед, которое для очень разреженной среды случайно расположенных
капель, каким является дождь, всегда когерентно. Представление о его роли в
ослаблении радиоволн в дождях различной интенсивности можно получить с помощью
спектральной зависимости альбедо однократного рассеяния
![]() , численно равного
отношению коэффициента рассеяния
, численно равного
отношению коэффициента рассеяния ![]() к коэффициенту ослабления
к коэффициенту ослабления
![]() ,
,
![]() /
/![]() , (рис. 4).
, (рис. 4).
Рис.4.
Спектральная зависимость альбедо однократного рассеяния элемента объема дождя
![]() при интенсивностях дождя R, равных 1 – 100 мм/ч, 2 – 12,5
мм/ч, 3 – 1,5 мм/ч.
при интенсивностях дождя R, равных 1 – 100 мм/ч, 2 – 12,5
мм/ч, 3 – 1,5 мм/ч.
Зависимости 1, 2, 3 на
рисунке относятся к интенсивностям дождя R, соответственно 100; 12,5 и 1,56 мм/ч. В расчетах
использованы: распределение капель по размерам Лоуса-Парсонса и значения
показателя преломления воды в каплях, найденные по формулам Рэя [33] для
температуры воды Т=20° С. Из рисунка следует, что вклад рассеяния в ослабление
радиоволн ММ и СМ диапазонов существенно различается. Так ослабление ММВ на 50%
определяется рассеянием излучения, причем, как показывают расчеты, для этой
части диапазона волн
![]() практически
не зависит от длины волны, интенсивности дождя, распределения капель по
размерам и термодинамической температуры воды в каплях. В диапазоне СМ волн
практически
не зависит от длины волны, интенсивности дождя, распределения капель по
размерам и термодинамической температуры воды в каплях. В диапазоне СМ волн
![]() является убывающей
степенной функцией длины волны излучения, зависит, также, от интенсивности
дождя, распределения капель по размерам и термодинамической температуры капель [34].
является убывающей
степенной функцией длины волны излучения, зависит, также, от интенсивности
дождя, распределения капель по размерам и термодинамической температуры капель [34].
В обзорах [35, 36] подробно рассмотрены особенности распространения поляризованного излучения ММВ в дожде. Причинами их появления являются: несферичность падающих капель дождя и наличие направления предпочтительной ориентации осей симметрии таких капель [33, 35]. Это находит выражение в спектральных зависимостях комплексных волновых чисел волн разных поляризаций.
Важнейшим свойством рассеяния ММВ в направлениях, отличных от направления вперед, является то, что для случайно распределенных в пространстве капель дождя его можно считать независимым. Это следует из того, что капли достаточно далеко удалены друг от друга (находятся в дальней волновой зоне по отношению друг к другу) и, таким образом, каждая капля взаимодействует с электромагнитной волной так, как если бы других капель не существовало. Это обстоятельство позволяет полагать, что рассеянное совокупностью различных капель излучение является некогерентным.
Рис.5. Нормированные индикатрисы рассеяния элемента объема дождя:
1 -
![]() = 1,4 мм; R = 12,5 мм/ч,
= 1,4 мм; R = 12,5 мм/ч,
2 -
![]() = 1,4 мм; R=1,56 мм/ч,
= 1,4 мм; R=1,56 мм/ч,
3 -
![]() = 2,2 мм; R=12,5 мм/ч,
= 2,2 мм; R=12,5 мм/ч,
4 -
![]() = 2,2 мм; R=1,56 мм/ч,
= 2,2 мм; R=1,56 мм/ч,
5 -
![]() = 3,3 мм; R=12,5 мм/ч,
= 3,3 мм; R=12,5 мм/ч,
6 -
![]() =3,3 мм; R=1,56 мм/ч,
=3,3 мм; R=1,56 мм/ч,
7 -
![]() = 8,6 мм; R= 12,5 мм/ч,
= 8,6 мм; R= 12,5 мм/ч,
8 -
![]() =8,6 мм ; R=1,56 мм/ч.
=8,6 мм ; R=1,56 мм/ч.
Угловое распределение
рассеянного элементом объема дождя неполяризованного излучения характеризуют
нормированной индикатрисой рассеяния. На рис.5 представлены индикатрисы
рассеяния радиоволн длиной l = 1,4; 2,2; 3,3 и 8,6 мм в дождях с интенсивностями R = 1,56 и 12,5 мм/ч. Расчеты выполнены
по теории Ми [37, 38] для распределения капель по размерам в соответствии с
законом Лоуса-Парсонса [33]. Несмотря на то, что форма индикатрисы рассеяния
излучения отдельной частицей многолепестковая [37] (число лепестков ~
![]() где
где
![]() -
модуль комлексного показателя преломления вещества частицы, а
-
модуль комлексного показателя преломления вещества частицы, а
![]() , здесь
, здесь
![]() - длина волны излучения
в свободном пространстве,
- длина волны излучения
в свободном пространстве,
![]() - радиус частицы), форма индикатрисы
рассеяния полидисперсной среды (каковой является дождь) весьма сглажена, но
эффект Ми [30-32, 37] хорошо выражен в диапазоне ММВ в отличие от диапазона СМ
волн, где индикатриса рассеяния близка к релеевской.
- радиус частицы), форма индикатрисы
рассеяния полидисперсной среды (каковой является дождь) весьма сглажена, но
эффект Ми [30-32, 37] хорошо выражен в диапазоне ММВ в отличие от диапазона СМ
волн, где индикатриса рассеяния близка к релеевской.
Эффект Ми состоит в том, что:
-главный лепесток значительно вытянут в направлении распространения волны;
-степень вытянутости индикатрисы зависит от длины волны излучения (растет с уменьшением длины волны), интенсивности дождя (более вытянут у дождей с большей интенсивностью) и формы функции распределения капель по размерам.
Из рис.5 видно, что
индикатриса рассеяния элемента объема дождя на длине волны
![]() = 8,6 мм близка по форме к
релеевской, а с уменьшением длины волны передний лепесток вытягивается, причем
анизотропия рассеяния тем больше, чем больше интенсивность дождя. Последнее
обстоятельство связано с тем, что с ростом интенсивности дождя растут число и
размеры крупных капель. Знание индикатрис полезно на практике, для оценки
уровня возможных помех между радиосистемами при рассеянии радиоволн в дождях [39-41],
и в теоретических исследованиях переноса радиотеплового СВЧ излучения в осадках
[42,43].
= 8,6 мм близка по форме к
релеевской, а с уменьшением длины волны передний лепесток вытягивается, причем
анизотропия рассеяния тем больше, чем больше интенсивность дождя. Последнее
обстоятельство связано с тем, что с ростом интенсивности дождя растут число и
размеры крупных капель. Знание индикатрис полезно на практике, для оценки
уровня возможных помех между радиосистемами при рассеянии радиоволн в дождях [39-41],
и в теоретических исследованиях переноса радиотеплового СВЧ излучения в осадках
[42,43].
В [39] показано, что индикатрисы рассеяния ММВ в дожде можно, с хорошей для практических применений точностью, аппроксимировать однопараметрическим соотношением, представляющим собой произведение индикатрис Релея и Хеньи-Гринстейна. Большей точности аппроксимации удалось достичь в [40] с помощью двухпараметрического выражения.
Упомянутое выше предположение о независимом рассеянии СВЧ излучения отдельными каплями в дождях позволяет существенно упростить оценку эффектов некогерентного многократного рассеяния, используя для этого хорошо развитую феноменологическую теорию переноса излучения. Так в [41] на базе численного решения векторной задачи переноса СВЧ излучения в дожде проанализировано влияние многократного рассеяния излучения на уровень взаимных помех между спутниковыми и приземными линиями связи. В [42, 43] выполнен анализ эффектов многократного рассеяния радиотеплового излучения в осадках и облаках. Показано [44], что в диапазоне ММВ важно учитывать вклады рассеяний высоких кратностей даже в дождях небольшой интенсивности и облаках.
3. Рефракция на приземных трассах
Распространение ММВ в приближении геометрической оптики может быть описано траекторией луча, а во многих практических случаях набором траекторных параметров - углами выхода и прихода луча, полной рефракции, геометрическим и видимым расстояниями.
Существующие методы расчета таких параметров не пригодны для всех вертикальных структур поля преломления и не позволяют найти траекторию луча по заданным истинным координатам пунктов связи, а также не определяют видимые координаты источника, наблюдаемого под малыми отрицательными углами места. С целью учета рефракции для модели сферически-слоистой атмосферы в ИРЭ РАН был разработан такой алгоритм, который позволил находить траектории, связывающие источник и приемник излучения при любых заданных как их координатах, так и вертикальных профилях коэффициента преломления [45]. Этот алгоритм, состоящий из компактных выражений, приспособлен для численных расчетов на ЭВМ. Он пригоден также и для случаев многолучевого распространения, когда конечные пункты могут быть связаны несколькими траекториями.
Алгоритм основан на описании траектории в слоистой среде с постоянными grad n в слоях, что приводит к искривлению траектории только внутри слоя, при этом преломления на границах слоев нет. Все возможные траектории находятся при сканировании по углу места. После того, как траектории вычислены, по ним определяется ослабление на трассе по методике [46]. Предложенный алгоритм позволяет также определять истинные координаты источника по видимым. Погрешность метода при расчете угловых величин в атмосфере оценивается в 1 угл. сек.
Этот подход был применен для оценки влияния метеоусловий на траекторные параметры волн миллиметрового и оптического диапазонов, распространяющихся вблизи горизонта в приземном слое атмосферы, где поле коэффициента преломления n подвержено сильным вариациям.
На основе данных метеонаблюдений ИЭМ на 15-ти уровнях мачты высотой ~ 301 м, полученных в годовом цикле 2-х суточных сеансов с интервалами в 6 часов внутри сеанса и 12 между ними, были рассчитаны текущие вертикальные профили n в миллиметровом и оптическом диапазонах. Для расчета n в ММ диапазоне была применена созданная в ИРЭ РАН инженерная методика расчета вращательной части диэлектрической проницаемости водяного пара, учитывающая спектральные зависимости преломления [47] и не приводящая к потере точности по сравнению с полным квантово-механическим расчетом [48].
Численное моделирование распространения в приземном слое выполнено для трассы с высотами передатчика и приемника 10 и 70 м соответственно, и дальностью 15 км. Обнаружена существенная связь характера отклонений видимого угла прихода от направления на источник с метеообстановкой. Для такой трассы определены средние и среднеквадратичные величины ошибки определения координат источника, амплитуда и фаза ее суточной компоненты и их зависимости от синоптической обстановки [50]. Получено, например, что максимальное изменение видимого угла в ММ диапазоне может составить около 20 угл. мин. в антициклональной ситуации теплого дня. В оптическом диапазоне это изменение на порядок меньше и фаза его отстает от ММВ на 6 - 7 часов.
По этим же метеоданным за
годовой период был проведен расчет статистических характеристик отклонений
углов прихода и выхода от истинного направления R1 и R2 у
приемника и передатчика соответственно и электрической длины пути между ними -
![]() [51].
[51].
Были вычислены коэффициенты корреляции между различными траекторными параметрами в каждом диапазоне волн и между соответствующими траекторными параметрами радио и оптических волн. В январе в большинстве случаев значения R1 и R2 в радиодиапазоне меньше, чем в оптике. В июле существенное влияние влажности приводит наоборот к большему диапазону изменения R1 и R2 на ММ волнах.
Средние за сутки
значения
![]() в
радиодиапазоне всегда больше, чем в оптическом. Средняя ошибка радиодальности
для рассмотренной трассы изменяется от 4,6 м зимой до 4,84 м летом при девиации
5 и 17 см соответственно. Годовой ход
в
радиодиапазоне всегда больше, чем в оптическом. Средняя ошибка радиодальности
для рассмотренной трассы изменяется от 4,6 м зимой до 4,84 м летом при девиации
5 и 17 см соответственно. Годовой ход
![]() в оптическом и ММ диапазонах
противоположен по фазе.
в оптическом и ММ диапазонах
противоположен по фазе.
Из результатов расчета
следует, что в целом корреляция между R1, R2 и
![]() в каждом диапазоне волн
и между диапазонами отсутствует.
в каждом диапазоне волн
и между диапазонами отсутствует.
Вышеприведенные результаты относятся к случаю фиксированных высот приемника и передатчика. Поскольку по расчетам было замечено, что траектория между ними не существует при определенных метеоусловиях, то анализировалась возможность отсутствия связи при изменении высоты передатчика от 2 до 301 м. По месяцам года были определены те минимальные высоты H2, при расположении источника выше которых, уже не наблюдались случаи отсутствия связи [52]. Эти высоты имеют сезонный ход и меняются от ~ 20 м в январе до ~ 60 м в июле. Отсутствие связи происходит из-за наличия слоев воздуха со сверхрефракционными свойствами между конечными пунктами трассы. Расчеты показывают, что на приземной трассе возможно не только отсутствие связи, но и возникновение многолучевости, обусловленной только особенностями преломления в атмосфере.
Прогноз условий распространения на трассе возможен при контроле высотного хода метеопараметров. Ошибки при их измерении могут заметно влиять на точность такого прогноза. В работе [53] изучено влияние погрешностей метеоизмерений на точность расчета траекторных параметров.
При расчетах вертикальной
рефракции атмосфера предполагалась горизонтально однородной. Обоснованность
этого предположения подтверждалась тем, что, во-первых, в экспериментах по
наблюдению Солнца в МГТУ на
![]() =3,3 мм [54] при компенсации
астрономической рефракции в реальном масштабе времени по методике [55] были
получены максимально возможные величины горизонтальной рефракции вблизи
горизонта, меньшие 10 угл. сек, и естественно, что на приземной трассе эта
величина будет существенно меньшей. Во-вторых, при измерении на приземной
трассе максимально возможная горизонтальная рефракция всегда была меньше ошибки
измерений, то есть меньше 1 угл.сек (см. [49] и [65]).
=3,3 мм [54] при компенсации
астрономической рефракции в реальном масштабе времени по методике [55] были
получены максимально возможные величины горизонтальной рефракции вблизи
горизонта, меньшие 10 угл. сек, и естественно, что на приземной трассе эта
величина будет существенно меньшей. Во-вторых, при измерении на приземной
трассе максимально возможная горизонтальная рефракция всегда была меньше ошибки
измерений, то есть меньше 1 угл.сек (см. [49] и [65]).
4. Турбулентность
Рассмотрим особенности влияния турбулентности на распространение миллиметровых волн. Наиболее адекватной моделью тропосферной турбулентности является локально-однородная и изотропная среда с Кармановским спектром флуктуаций показателя преломления n:
где
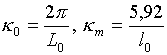 ,
,
![]() и
и ![]() - внешний и
внутренний масштабы турбулентности, Cn - структурная
характеристика показателя преломления. В окнах прозрачности ММ и СМ диапазонах
волн Cn, характеризующая интенсивность флуктуаций показателя
преломления, практически не зависит от длины волны. Такое
описание турбулентных неоднородностей показателя преломления применимо для
трасс с небольшим перепадом высот, когда ширина пучка много меньше высоты
трассы и влиянием конвекции можно пренебречь. Метод решения задачи
распространения в локально-однородной и изотропной среде зависит от соотношения
длины волны
- внешний и
внутренний масштабы турбулентности, Cn - структурная
характеристика показателя преломления. В окнах прозрачности ММ и СМ диапазонах
волн Cn, характеризующая интенсивность флуктуаций показателя
преломления, практически не зависит от длины волны. Такое
описание турбулентных неоднородностей показателя преломления применимо для
трасс с небольшим перепадом высот, когда ширина пучка много меньше высоты
трассы и влиянием конвекции можно пренебречь. Метод решения задачи
распространения в локально-однородной и изотропной среде зависит от соотношения
длины волны
![]() ,
протяженности трассы и внешнего и внутреннего масштабов турбулентности, а
именно, от соотношения между длиной трассы L,
,
протяженности трассы и внешнего и внутреннего масштабов турбулентности, а
именно, от соотношения между длиной трассы L, ![]() и
и
![]() . Для типичных значений параметров
. Для типичных значений параметров
![]() = 1 мм,
= 1 мм,
![]() = 10
м получаем, что в ММ и СМ диапазоне
= 10
м получаем, что в ММ и СМ диапазоне
![]() для всех длин волн этих диапазонов,
а
для всех длин волн этих диапазонов,
а ![]() может быть
как больше, так и меньше длины трассы L, т.е. в отличие от оптического
диапазона волн метод геометрической оптики не применим для описания
распространения ММВ в турбулентной среде. Для ММ и СМ волн наиболее приемлемым
для нахождения статистических характеристик флуктуации амплитуды и фазы
является метод плавных возмущений (МПВ), учитывающий многократное рассеяние и дифракционные
эффекты [56]. Для большинства задач, связанных с распространением узких
пучков излучения, можно положить
может быть
как больше, так и меньше длины трассы L, т.е. в отличие от оптического
диапазона волн метод геометрической оптики не применим для описания
распространения ММВ в турбулентной среде. Для ММ и СМ волн наиболее приемлемым
для нахождения статистических характеристик флуктуации амплитуды и фазы
является метод плавных возмущений (МПВ), учитывающий многократное рассеяние и дифракционные
эффекты [56]. Для большинства задач, связанных с распространением узких
пучков излучения, можно положить
![]() .
.
В развитие [56, 57], где рассмотрены случаи плоской и сферической волн в [58, 59] исследовано распространение гауссова пучка ММВ в приземном слое турбулентной атмосферы. Поскольку одним из преимуществ этого диапазона является возможность формирования узконаправленных пучков излучения, учет распределения поля по апертуре передающей антенны весьма важен для получения количественных оценок интенсивности флуктуаций амплитуды и фазы поля.
Основной параметр,
характеризующий распространение пучка в турбулентной среде, - это волновой
параметр
![]() , где
, где
![]() -
волновой вектор,
-
волновой вектор,
![]() -
эффективный радиус пучка вблизи передающей антенны. Предельные случаи P<<1 и P>>1 соответствуют плоской и сферической
волнам. Как в ММ, так и в СМ диапазоне для трасс порядка нескольких километров
в пределах прямой видимости значения P достаточно велики. Так например, при L = 10 км,
-
эффективный радиус пучка вблизи передающей антенны. Предельные случаи P<<1 и P>>1 соответствуют плоской и сферической
волнам. Как в ММ, так и в СМ диапазоне для трасс порядка нескольких километров
в пределах прямой видимости значения P достаточно велики. Так например, при L = 10 км,
![]() = 2,2 мм и
= 2,2 мм и
![]() = 0,5 м P =14.
= 0,5 м P =14.
Решена задача нахождения
статистических характеристик флуктуаций амплитуды, фазы, угла прихода гауссова
пучка ММВ в слабопоглощающей турбулентной среде с пространственным спектром флуктуаций
показателя преломления вида (1), причем для расчета структурной характеристики
показателя преломления использовалась методика, изложенная в [60].
Получены асимптотические формулы для среднеквадратичных флуктуаций уровня
амплитуды, угла прихода в случае точечного приемника, проанализированы
структурные и корреляционные функции флуктуаций уровня амплитуды и фазы как в
окнах прозрачности, так и вблизи линий поглощения ММ диапазона. Заметим, что
средний квадрат уровня амплитуды
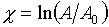 (A – амплитуда поля в турбулентной
среде, A0 - амплитуда поля в свободном пространстве) при
малых относительных флуктуациях амплитуды
(A – амплитуда поля в турбулентной
среде, A0 - амплитуда поля в свободном пространстве) при
малых относительных флуктуациях амплитуды
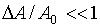 совпадает со средним квадратом этой
величины, т. е.
совпадает со средним квадратом этой
величины, т. е.
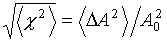 .
.
Показано, что средний
квадрат уровня амплитуды
![]() пучка ММВ зави-сит лишь от длины
волны и длины трассы и не зависит от размеров пучка:
пучка ММВ зави-сит лишь от длины
волны и длины трассы и не зависит от размеров пучка:
Среднеквадратичные флуктуации амплитуды пучка ММВ в 1,8 раза меньше, чем для плоской волны [56]. Следует отметить, что рассмотренная модель турбулентности применима для расчета флуктуаций амплитуды поля в полосе частот от десятых долей Гц до 20 Гц, вызванных быстрыми изменениями показателя преломления.
Структурная функций
флуктуаций фазы пучка ММВ Df монотонно возрастает с увеличением
разноса точек приема
![]() .
Так например при значении волнового параметра P =80 (это соответствует
.
Так например при значении волнового параметра P =80 (это соответствует
![]() = 2,2 мм,
= 2,2 мм,
![]() = 0,3 м и L = 20
км, Cn = 0,5´10-6 м-1/3 - лето)
для
= 0,3 м и L = 20
км, Cn = 0,5´10-6 м-1/3 - лето)
для
![]() = 1 м
= 1 м
![]() = 1,5x10-6, т. е.
среднеквадратичная разность фаз между точками, разнесенными на 1 м (одна из них
- на оси пучка) составляет 4 угл. мин.
= 1,5x10-6, т. е.
среднеквадратичная разность фаз между точками, разнесенными на 1 м (одна из них
- на оси пучка) составляет 4 угл. мин.
Исследовано также влияние
усредняющего действия приемной апертуры на интенсивность флуктуаций амплитуды.
Показано [58], что функция усреднения Qm,
характеризующая отношение дисперсии флуктуаций амплитуды на выходе приемной
антенны радиуса ![]() к
дисперсии флуктуаций амплитуды в случае точечного приемника, может быть
аппроксимирована выражением вида
к
дисперсии флуктуаций амплитуды в случае точечного приемника, может быть
аппроксимирована выражением вида
где b = 1,6 для длин волн ММ диапазона.
Среднеквадратичные флуктуации
направления распространения пучка ММВ в случае точечного приемника определяются
не внутренним масштабом турбулентности, как в случае плоской монохроматической
волны, а эффективным начальным радиусом пучка
![]() [58]:
[58]:
Установлено, что поглощение в ММ и СБММ диапазоне не оказывает существенного влияния на интенсивность флуктуаций амплитуды, фазы и направления распространения пучка ММВ – его влияние составляет доли процента даже вблизи линий поглощения.
В таблице 1 приведены
значения
![]() в
процентах и дисперсии направления распространения пучка ММВ
в
процентах и дисперсии направления распространения пучка ММВ
![]() в угловых
секундах для различных длин волн l в зависимости от длины трассы L при
в угловых
секундах для различных длин волн l в зависимости от длины трассы L при
![]() = 0,3 м, Cn = 0,5´10-6 м-1/3 (лето).
= 0,3 м, Cn = 0,5´10-6 м-1/3 (лето).
Таблица 1. Средний квадрат флуктуаций уровня амплитуды и дисперсия направления распространения пучка ММВ.
|
|
||||
|
длина волны, мм |
L, км |
|||
| 5 | 10 | 20 | 30 | |
|
2.20 |
3.8 | 7.2 | 13.6 | 19.8 |
|
3.30 |
3.0 | 5.7 | 10.8 | 15.6 |
|
8.60 |
1.7 | 3.3 | 6.2 | 8.9 |
|
дисперсия
направления распространения
|
||||
|
8.60 |
2.2-8.6 |
15.5 | 21.9 |
38.0 |
При сравнении экспериментальных данных с теоретическими расчетами следует иметь в виду, что для корректного сопоставления с приведенными в этом разделе результатами необходимо выделить в спектре амплитудных флуктуаций и флуктуаций угла прихода участок, соответствующий инерционному интервалу турбулентности – ориентировочно от 0,1 Гц до 20 Гц.
Исследовано также влияние турбулентности на распространение широкополосного сигнала ММ диапазона [61].
Расчеты, выполненные для трасс протяженностью 15 и 30 км, частот 34,9 и 136,4 ГГц, соответствующих окнам прозрачности атмосферы, и радиуса пучка 30 см, показали, что при разносе частот порядка 10 ГГц модуль функции когерентности спадает на 2 - 6%. При распространении одиночного гауссовского импульса с полушириной 0,1 нс в окнах прозрачности гауссовская форма огибающей практически сохраняется, а эффективная длительность незначительно увеличивается - например, на частоте 136,4 ГГц и трассе 30 км относительное уширение не превосходит 1 - 2 %.
5. Экспериментальные исследования
В ИРЭ РАН совместно МГТУ им. Баумана организована специальная трасса распространения на базе радиотелескопа ММ диапазона РТ-7,5, который использован в качестве приемной антенны.
В течение двух лет параллельно проведено две серии экспериментов. В одной из них исследовались статистические характеристики ММ волн, а именно: флуктуации интенсивности и угла прихода, обусловленные атмосферной турбулентностью. В другой серии исследовалась угловая рефракция, вызванная стратификацией приземного слоя атмосферы (ПСА).
Результаты этих исследований представлены также в [49, 62-66].
5.1. Аппаратура и методика экспериментов
Трасса распространения, на которой проводились эксперименты, создана в Дмитровском районе Московской области. Длина трассы, угол наклона и средняя высота составляют 13,7 км, 8 угл.мин и 35 м соответственно. Подстилающую поверхность трассы составляют сельскохозяйственные угодья, небольшие рощи, водный канал и часть города Дмитрова – места расположения передатчика. Точка приема – радиотелескоп РТ-7,5, диаметр апертуры которого 7,8 м, а угловое разрешение 2 угл.мин на частоте 90 ГГц [67, 68]. Столь высокое разрешение полностью устраняет возможность приема волн, отраженных от подстилающей поверхности трассы. Передатчик представляет собой стабилизированный по частоте и по мощности генератор на лампе обратной волны, питающий параболическую антенну с угловым разрешением 30 угл.мин.
5.1.1. Для измерений флуктуаций ММВ разработана специальная приемная система, основанная на принципе конического сканирования луча антенны РТ-7,5. Эта аппаратура обеспечивает одновременное измерение и регистрацию флуктуаций интенсивности, флуктуаций вертикальной и горизонтальной составляющих угла прихода, а также медленные (до 3-х часов) изменения вертикальной компоненты угла прихода, обусловленные рефракцией. Упрощенная блок-схема приемной системы представлена на рис. 6.
Рис.6. Блок-схема аппаратурного комплекса для исследования стохастических вариаций амплитуды и угла прихода ММ волн.
Коническое сканирование луча радиотелескопа обеспечивается с помощью дискового контррефлектора (К), расположенного у первичного фокуса РТ-7,5. Волна, сфокусированная антенной РТ-7,5 (А) и отраженная контррефлектором, поступает на вход супергетеродинного приемника (П) [69], находящегося во вторичном фокусе. Контррефлектор вращается с частотой 137 Гц вокруг своей оси с помощью электродвигателя (ЭД), а плоскость диска К слегка наклонена относительно оси вращения так, что луч антенны вращается по конической поверхности с образующим углом 110 угл.сек. Таким образом, если существует небольшая разность (менее 40 угл.сек) между видимым направлением на передатчик и осью антенны, то выходной сигнал приемника будет модулирован по амплитуде с частотой вращения контррефлектора. Глубина модуляции пропорциональна отклонению оси антенны от угла прихода волны, а фаза модуляции определяется направлением этого отклонения.
В низкочастотной части системы информация, содержащаяся в выходном сигнале приемника, обрабатывается и распределяется по пяти каналам. В двух каналах, снабженных синхронными детекторами (СДВ, СДГ), генератором опорной частоты (ГОЧ) и цифровым фазовращателем (ЦФВ) выходные напряжения определяются соответственно вертикальной и горизонтальной компонентами угла прихода, умноженными на интенсивность принимаемого излучения. Зависимости выходных напряжений от угла прихода в этих каналах описываются пеленгационными характеристиками, имеющими линейных участок шириной около 70 угл.сек. В двух других каналах с помощью полосового фильтра (ПФ), амплитудного детектора (АД) и селективных усилителей (СУБ, СУМ) формируются напряжения пропорциональные соответственно быстрым флуктуациям (10-1-10 Гц) и медленным изменениям (10-3 -10-1 Гц) интенсивности.
Из-за изменений стратификации атмосферы в ходе длительных измерений флуктуаций среднее значение вертикальной составляющей угла прихода может измениться на величину до нескольких угловых минут и выйти за пределы линейного участка пеленгационной характеристики. Для того, чтобы преодолеть это ограничение, ось вращения контррефлектора К автоматически поворачивается в вертикальной плоскости с помощью специального электро-механического привода (ЭМП), напряжением питания которого является интегрированный по времени выходной сигнал канала вертикальной составляющей угла прихода, подаваемый в виде отрицательной обратной связи через усилитель УМ. Угловое положение оси вращения, зависящее от среднего значения угла прихода волны, измеряется датчиком ДУ и регистрируется.
В ходе экспериментов вся выходная информация приемной системы регистрировалась на многоканальном магнитографе (М) с частотной модуляцией. Затем она оцифровывалась и вводилась в память компьютера (К) для последующей статистической обработки.
Параметры приемной системы были тщательно рассчитаны и измерены. Расчетная угловая чувствительность составила 0,01 угл.сек, измеренная – 0,06 угл.сек. Отношение "сигнал-шум" 60 дБ. Взаимное влияние вертикального и горизонтального угловых каналов –18 дБ. Частотный диапазон измеряемых флуктуаций 10-3 –10 Гц.
5.1.2. Долговременные (до 24-х часов) вариации угла прихода, обусловленные регулярной рефракцией, исследовались с помощью радиометрического приемника [69], установленного в первичном фокусе РТ-7,5, а диаграммная модуляция была заменена на амплитудную. Методика измерений состояла в сканировании антенны РТ-7,5 в вертикальной или горизонтальной плоскостях относительно направления на передатчик. Сканирование выполнялось в виде пятиминутных серий по 10 сканов каждая. Затем результаты каждой серии усреднялись. Случайная ошибка измерений составила 1 угл.сек. Во время получасовых интервалов между сериями приемная антенна наводилась на передатчик для того, чтобы измерять текущие значения флуктуаций интенсивности принимаемого излучения и найти связь между флуктуациями и рефракцией.
Некоторые измерения угловой рефракции ММВ сопровождались синхронными измерениями рефракции в оптическом (видимом) диапазоне. Оптические измерения выполнялись совместно с Горьковским инженерно-строительным институтом с помощью геодезического теодолита с точностью 1 угл.сек. Источником оптического излучения служил осветительный прожектор, установленный на передающем пункте.
5.2. Результаты
5.2.1. В различных погодных и
сезонных условиях проведено 9 сеансов непрерывных измерений флуктуаций с общим
временем 12 часов. Получены среднеквадратичные величины флуктуаций
интенсивности si, флуктуаций вертикальной sв и горизонтальной sг
составляющих угла прихода. Значения si, sв и sг вычислялись по 40-секундным
интервалам записи сигналов. С использованием теории распространения
электромагнитных волн, разработанной Татарским В.И. [56], и выражений для si, sв и sг для гауссового пучка
электромагнитных волн [58] по результатам каждого сеанса вычислялись значения
структурной характеристики турбулентности Cn. Полученные данные представлены в
таблице 2, где Cni и Cna - значения Cn , вычисленные отдельно по si и sв, sг, причем среднеквадратичная величина
флуктуаций угла прихода вычислялась как геометрическая сумма sв и sг; t и p соответственно температура и давление
воздуха, е- парциальное давление водяного пара, ![]() - скорость ветра.
Разность величин Cni и Cna достигает 250%, что в данном случае
определяет точность теоретических выражений для si, sв и sг.
- скорость ветра.
Разность величин Cni и Cna достигает 250%, что в данном случае
определяет точность теоретических выражений для si, sв и sг.
В большинстве экспериментов отмечалась существенная анизотропия турбулентности, которая проявлялась в отличии sв от sг. Иногда отношение sв и sг достигало 2,5.
Исследования спектрального состава флуктуаций показали, что в области частот, соответствующих инерционному интервалу турбулентности (порядка 0,1 Гц и выше) усредненный наклон спектров составляет –2,2, в то время как его теоретическое значение равно –2,67 (-8/3) [56]. В низкочастотной области (менее 0,1 Гц), которая не описывается теоретически, отмечается существенное отличие спектров для вертикальной и горизонтальной составляющих угла прихода, которое свидетельствует о возрастании степени анизотропии турбулентности с уменьшением пространственной частоты турбулентных неоднородностей. Это означает, что более крупные неоднородности имеют плоско-слоистую форму.
Таблица 2.
|
Дата, время |
si , % |
sв,, угл. сек. |
sг , угл. сек. |
Сni *107, м-1/3 |
Сna *107, м-1/3 |
Метеоусловия |
|||
|
t, oC |
p, мб |
е, мб |
v, м/с |
||||||
|
4 мая 16.03-16.50 |
0,61- -0,71 |
0,81- -1,6 |
0,96- -1,6 |
0,20- -0,39 |
0,64- -1,1 |
+8,8 |
992 |
9,8 |
2 |
|
4 мая 16.55-18.07 |
0,34- -0,64 |
0,45- -0,85 |
0,56- -1,0 |
0,18- -0,34 |
0,38- -0,70 |
+8,9 |
994 |
10,5 |
2 |
|
18 мая 00.23-02.42 |
0,91- -1,6 |
0,70- -2,1 |
1,32- -4,0 |
0,48- -0,86 |
0,82- -2,4 |
+10,5 |
992 |
10,2 |
1 |
|
18 мая 13.24-15.50 |
3,6- -6,1 |
1,0- -2,8 |
1,4- -4,2 |
1,8- -3,2 |
1,1- -2,8 |
+17,6 |
996 |
8,1 |
6 |
|
27 дек. 12.20-13.40 |
0,27- -0,88 |
0,40- -0,90 |
0,30- -0,81 |
0,14- -0,46 |
0,26- -0,64 |
-6,1 |
1004 |
3,5 |
4 |
|
27 дек. 13.50-16.10 |
0,56- -1,3 |
0,18- -0,30 |
0,15- -0,20 |
0,31- -0,69 |
0,16- -0,24 |
-5,5 |
1006 |
3,9 |
3 |
|
16 янв. 19.07-20.03 |
0,20- -0,61 |
0,70- -1,6 |
0,35- -0,70 |
0,11- -0,32 |
0,38- -0,91 |
-8,6 |
970 |
2,8 |
5 |
|
17 янв. 12.00-12.28 |
0,20- -0,30 |
0,25- -0,41 |
0,20- -0,35 |
0,10- -0,16 |
0,17- -0,26 |
-7,3 |
979 |
3,0 |
2 |
|
17 янв. 15.09-17.15 |
1,0- -1,8 |
0,41- -0,72 |
0,40- -0,68 |
0,53- -0,92 |
0,31- -0,53 |
-6,9 |
976 |
3,1 |
2 |
Относительное расхождение полученных экспериментальных данных и результатов теоретических расчетов по [56, 58] объясняется влиянием подстилающей поверхности на структуру турбулентности ПСА, особенно на ее крупномасштабную часть. Можно заключить, что модель однородной изотропной турбулентности, используемая в [56, 58], недостаточно точна для теоретических расчетов параметров ММВ в ПСА.
Обнаружено, что распределение флуктуаций интенсивности ММВ подчиняется логарифмически-нормальному закону, а распределение флуктуаций углов прихода – нормальному.
Флуктуации интенсивности и углов прихода между собой не коррелируют (коэффициенты корреляции на интервалах времени 40 сек всегда были меньше 0,2).
5.2.2. Эксперименты по угловой рефракции выполнялись в течение двух-годового цикла в форме тринадцати 30-часовых сеансов непрерывных измерений с общим временем 370 часов.
Измеренные максимальные величины угла рефракции (угловой разности между видимым и истинным направлением на передатчик) и скорости его изменения для вертикальной компоненты угла прихода по результатам всех экспериментов составили соответственно 5 угл. мин и 3 угл. мин/час осенью при антициклональной погоде.
При одновременных измерениях рефракции по вертикали и горизонтали изменение угла горизонтальной рефракции всегда было меньше ошибки измерений (1 угл. сек). Таким образом, горизонтальная рефракция, по крайней мере, на два порядка меньше вертикальной, что согласуется с известными данными о структуре ПСА [70]. Поэтому все приведенные ниже результаты относятся только к рефракции по вертикали.
По двух-годовому циклу измерений получен закон распределения углов рефракции, который оказался несимметричным и достаточно точно был аппроксимирован гамма-распределением. Среднее значение угла рефракции и его среднеквадратичный разброс составили соответственно 70 и 50 угл.сек.
В среднем рефракция ночью в 2-3 раза больше, чем днем; летом в 2 раза больше, чем зимой. В ряде экспериментов максимальные величины рефракции отмечались в моменты восхода и захода Солнца, что связано с подъемом инверсионных слоев температуры и влажности ПСА в утренние и вечерние часы.
Спектры изменений угла рефракции в диапазоне частот 10-5-10-3 Гц очень изменчивы в зависимости от погодных и сезонных условий. Однако, эти спектры, как правило, имеют два максимума, один из которых соответствует превышению дневной рефракции относительно ночной (период колебаний 24 часа), другой отражает эффект роста рефракции при восходе - заходе Солнца (период около 12 часов). В усредненном по всем измерениям спектре 24-часовой максимум в три раза больше 12-часового.
По результатам проведенных двух серий экспериментов построены обобщенные спектры вариаций вертикальной и горизонтальной составляющих угла прихода ММ излучения в диапазоне частот 10-5 -10 Гц (периоды колебаний от 0,1 сек до 30 часов). Эти спектры показаны на рис.7, где В - спектр вертикальной компоненты, Г – горизонтальной. Вертикальными отрезками на спектре В показаны диапазоны сезонных и погодных вариаций спектральной плотности.
Рис.7. Обобщенные спектры вариаций вертикальной (В) и горизонтальной (Г) составляющих угла прихода ММ волн. Вертикальными отрезками на кривых В и Г показан диапазон сезонных и погодных изменений спектральной плотности.
Какая-либо устойчивая связь между основными параметрами атмосферы, измеренными вблизи земной поверхности, рассчитанным по ним показателем преломления воздуха, уровнем флуктуаций интенсивности принимаемого излучения и углом рефракции не обнаружена. Коэффициенты корреляции между перечисленными величинами в среднем не превышали 0,2.
В результате одновременных измерений рефракции ММВ и оптического излучения обнаружено, что в летний период нет устойчивой связи между углами рефракции в этих диапазонах (коэффициент корреляции 0,4), тогда как зимой корреляция достигала значения 0,97. Это обусловлено тем, что с понижением температуры понижается абсолютная влажность воздуха и, следовательно, уменьшается вызванное ей различие в показателях преломления и траекториях лучей для ММ и оптических волн.
6. Влияние подстилающей поверхности на распространение миллиметровых волн
В дециметровом и сантиметровом диапазонах волн слабо шероховатые поверхности раздела воздуха и Земли являются зеркально отражающими. Такое отражение описывается формулами Френеля [73, 74]. В тех же условиях на ММВ среднеквадратичные неровности поверхностей соизмеримы с длиной волны. Неровности поверхности играют значительную роль и некогерентная составляющая рассеянного поля становится преобладающей. Но даже при этих условиях пространственная интерференционная структура поля ММВ на сравнительно малых расстояниях и малых углах скольжения проявляется [77]. С ростом расстояний от источника излучения до точки приема зона эффективного отражения, существенная для формирования интерференционной картины, увеличивается и включает как мелкомасштабные, так и крупномасштабные неровности, которые могут привести к разрушению интерференционной структуры. К тому же начинают проявляться флуктуации амплитуды, фазы и направления распространения, которые искажают интерференционную структуру суммарного поля [75-77].
В [77] была рассмотрена задача нахождения поля ММВ в канале связи с учетом турбулентности среды и подстилающей поверхности. Показано, что комплексная фаза флуктуационного поля определяется суммой трех слагаемых. Первое из них обусловлено прямой волной, второе и третье описывают суперпозицию волн, рассеянных на турбулентных неоднородностях и переотраженных поверхностью. Задача решалась в предположении высоко поднятых источника и приемника излучения. Однако больший интерес для практического использования представляет решение задачи при небольших высотах, на которых располагаются передающая и приемная антенны.
Для малых углов
скольжения до сих пор нет удовлетворительного теоретического решения задач
рассеяния поверхностями с хаотическими неровностями. Параметр Релея
![]() (где k – волновой вектор,
(где k – волновой вектор,
![]() - дисперсия высот неровностей,
- дисперсия высот неровностей,
![]() -угол
скольжения) при
-угол
скольжения) при
![]() ~ 2¸3 мм,
~ 2¸3 мм,
![]() = 2¸6°
становится много меньше единицы, а при выполнении условия
= 2¸6°
становится много меньше единицы, а при выполнении условия
![]() для описания структуры поля
справедлива формула, аналогичная формуле для гладкой поверхности [73] (здесь r¢ - расстояние от точки наблюдения до
зеркального изображения передатчика). Для неровностей с нормальным распределением
высот средний коэффициент отражения
для описания структуры поля
справедлива формула, аналогичная формуле для гладкой поверхности [73] (здесь r¢ - расстояние от точки наблюдения до
зеркального изображения передатчика). Для неровностей с нормальным распределением
высот средний коэффициент отражения
![]() в приближении метода касательной плоскости (МКП) записывается
в виде [75]:
в приближении метода касательной плоскости (МКП) записывается
в виде [75]:
где
![]() -модуль френелевского коэффициента
отражения по полю для вертикальной (В) и горизонтальной (Г) поляризаций.
-модуль френелевского коэффициента
отражения по полю для вертикальной (В) и горизонтальной (Г) поляризаций.
 Отсутствие строгих решений обусловило
необходимость получения экспериментальных данных, т.к. они дают не только
количественные сведения, но и позволяют сделать феноменологическое описание
процессов.
Отсутствие строгих решений обусловило
необходимость получения экспериментальных данных, т.к. они дают не только
количественные сведения, но и позволяют сделать феноменологическое описание
процессов.
Измерение интерференционной структуры поля на волне 2×мм проводилось в натурных условиях над специально подготовленной (выровненной и выдержанной при различных погодных условиях) песчаной поверхностью и над этой же площадкой, покрытой слоем снега толщиной 30 см. Для исключения влияния турбулентности атмосферы расстояние от передатчика до приемника составляло 150 м. Схема эксперимента описана в [75]. Приемник устанавливался на телескопической мачте, которая могла равномерно подниматься от 3 до 10 м. При перемещении приемника по вертикали регистрировались интерферограммы суммарного поля.
Рис.8. Интерферограмма структуры поля
ММВ (![]() =2×10-3
м) над песчаным покровом для горизонтальной
поляризации.
=2×10-3
м) над песчаным покровом для горизонтальной
поляризации.
По записям
интерференционной структуры поля по методике, описанной в [75], были рассчитаны
коэффициенты отражения для горизонтальной и вертикальной поляризаций от
песчаной и снежной поверхностей. На рис.8 приведен фрагмент зависимости глубины
интерференции от высоты приемника или угла скольжения ![]() над песчаным покровом
для горизонтальной поляризации. Интерферограммы для вертикальной поляризации и
над снежным покровом [75] аналогичны приведенной на
рис.8.
над песчаным покровом
для горизонтальной поляризации. Интерферограммы для вертикальной поляризации и
над снежным покровом [75] аналогичны приведенной на
рис.8.
Рис.9. Зависимость коэффициентов
отражения ММВ от угла скольжения υ на волне
![]() =2 мм для песчаной поверхности:
=2 мм для песчаной поверхности:
1, 2- расчет коэффициентов отражения по формулам Френеля для горизонтальной |V|Г и вертикальной |V|В
поляризаций для гладкой поверхности с
![]() =2,5 – i 6,2 ×10-2;
=2,5 – i 6,2 ×10-2;
3, 4 — аппроксимация
экспериментальных значений коэффициентов отражения выражением (5) по методу
наименьших квадратов, соответствующих
![]() , для горизонтальной и
вертикальной поляризаций
, для горизонтальной и
вертикальной поляризаций
соответственно;
5, 6 - экспериментальные значения соответственно для горизонтальной и вертикальной поляризаций.
На рис.9 показана
зависимость коэффициентов отражения ММВ от угла скольжения для песчаной
поверхности. Полученные коэффициенты отражения для песчаной и снежной
поверхностей использовались для оценки их среднеквадратичных неровностей.
Теоретические кривые на
рис.9 построены для
![]() Из этого следует, что при
Из этого следует, что при
![]() = 2,2 мм значения
= 2,2 мм значения
![]() 2,65 мм. Аналогично были
оценены среднеквадратичные неровности для снега, которые по порядку величин
совпали со значением
2,65 мм. Аналогично были
оценены среднеквадратичные неровности для снега, которые по порядку величин
совпали со значением
![]() для
песка.
для
песка.
При расстояниях между передающим и приемным пунктами несколько километров и высотах антенн над поверхностью земли ~ 10 ¸ 15 м суперпозиция когерентной составляющей волны, отраженной подстилающей поверхностью, и прямой волны приводит к интерференционному распределению суммарного поля с глубокими амплитудными замираниями [76]. Однако взаимодействие этих волн с турбулентными неоднородностями показателя преломления атмосферы обуславливает то, что поля этих волн в плоскости приема имеют случайную структуру. В результате происходит искажение интерференционной картины.
Решение задачи
было предложено в [76]. По аналогии с линейными радиотехническими фильтрами
вводят частотную характеристику атмосферного радиоканала
![]() , которую при линейном взаимодействии
электромагнитной волны с невозмущенной средой распространения определяют как
отношение поля
, которую при линейном взаимодействии
электромагнитной волны с невозмущенной средой распространения определяют как
отношение поля
![]() плоской волны на выходе канала
протяженностью x и поля на входе
плоской волны на выходе канала
протяженностью x и поля на входе
![]() :
:
Здесь
![]() ,
,
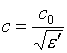 - скорость распространения волны в радиоканале,
- скорость распространения волны в радиоканале,
![]() - комплексный
показатель преломления. Модуль
- комплексный
показатель преломления. Модуль
![]() соответствует амплитудной частотной характеристике
(АЧХ), а
соответствует амплитудной частотной характеристике
(АЧХ), а
![]() -
фазочастотной характеристике. Таким образом, частотная характеристика
представляет собой комплексную амплитуду поля плоской волны с волновым числом,
выраженным через угловую частоту, показатель преломления n и коэффициент поглощения m среды распространения. Тогда влияние
турбулентности и отражений подстилающей поверхностью можно учесть
статистическим усреднением, в результате чего получим когерентную составляющую
комплексной амплитуды поля плоской волны.
-
фазочастотной характеристике. Таким образом, частотная характеристика
представляет собой комплексную амплитуду поля плоской волны с волновым числом,
выраженным через угловую частоту, показатель преломления n и коэффициент поглощения m среды распространения. Тогда влияние
турбулентности и отражений подстилающей поверхностью можно учесть
статистическим усреднением, в результате чего получим когерентную составляющую
комплексной амплитуды поля плоской волны.
Отсюда следует, что
среднестатистическую комплексную частотную характеристику (ЧХ) радиоканала с
учетом турбулентности атмосферы и отражений подстилающей поверхностью можно
представить в виде произведения парциальных ЧХ (по аналогии с многозвенным
линейным фильтром): ЧХ слоя протяженностью r турбулентной атмосферы ![]() и ЧХ полупространства, ограниченного подстилающей
поверхностью
и ЧХ полупространства, ограниченного подстилающей
поверхностью
![]()
В [76] показано, что для
реальных условий состояния турбулентной атмосферы влияние амплитудных и фазовых
флуктуаций на
![]() существенно
меньше влияния молекулярного поглощения, и АЧХ слоя турбулентной атмосферы
определяется спектральной зависимостью молекулярного поглощения [78].
существенно
меньше влияния молекулярного поглощения, и АЧХ слоя турбулентной атмосферы
определяется спектральной зависимостью молекулярного поглощения [78].
Так как ЧХ радиоканала с учетом подстилающей поверхности определяется через статистическое среднее поле волны в плоскости приема, то учет влияния неровностей подстилающей поверхности проводится с использованием статистических средних коэффициентов отражения <V> [75] , а среднюю суперпозицию полей в точке приема можно представить в виде
где Δr -разность
хода прямой и отраженной подстилающей поверхностью волн. Тогда для
![]() можно записать [76]:
можно записать [76]:
где
![]() - разность комплексных фаз
интерферирующих волн в точке приема.
- разность комплексных фаз
интерферирующих волн в точке приема.
Без учета
флуктуаций (![]() ) и
поглощения (m
= 0) при n = 1, для поверхности с
) и
поглощения (m
= 0) при n = 1, для поверхности с
![]() , т.е. │<V>│=│V│=1 и
, т.е. │<V>│=│V│=1 и
![]() , выражение (9)
преобразуется к виду [76]:
, выражение (9)
преобразуется к виду [76]:
В (10) учтено, что
![]() , где zi и z0 - высоты приемника и передатчика, L - расстояние между передатчиком и приемником. В
аргумент (10) высота приемника
, где zi и z0 - высоты приемника и передатчика, L - расстояние между передатчиком и приемником. В
аргумент (10) высота приемника
![]() и частота
и частота
![]() входят симметрично. Это было использовано
для получения экспериментальной реализации АЧХ, т.к. варьирование высотой
приемника (углы прихода
входят симметрично. Это было использовано
для получения экспериментальной реализации АЧХ, т.к. варьирование высотой
приемника (углы прихода
![]() ) эквивалентно изменению частоты
) эквивалентно изменению частоты
![]() . Максимум j -ого экстремума интерференционной
структуры поля соответствуют частотам
. Максимум j -ого экстремума интерференционной
структуры поля соответствуют частотам
![]() Тогда ширина полосы частот, пропускаемая
радиоканалом, будет определяться из условия
Тогда ширина полосы частот, пропускаемая
радиоканалом, будет определяться из условия
![]() , откуда следует, что
, откуда следует, что
Измерения АЧХ атмосферного радиоканала осуществлялись по схеме измерения интерференционной структуры поля – аналогично измерению эффективных коэффициентов отражения по той же методике и на той же аппаратуре. Они проводились на трассе протяженностью 3200 м над песчаной поверхностью. Ширина диаграммы направленности передающей антенны по половинному уровню мощности равна 20΄.
В [76] показано, что величина амплитудных флуктуаций сравнима с глубиной интерференционных замираний в отсутствии турбулентной среды, что затрудняет визуальное наблюдение периодической структуры суммарного поля в реальных условиях.
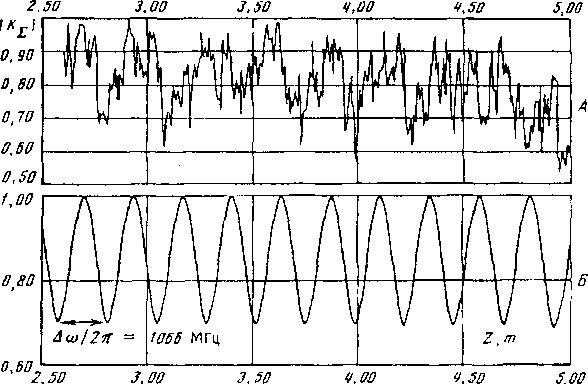
На рис.10а приведен фрагмент записи реализации АЧХ. Для построения среднеквадратической АЧХ, аналогично [75], по экспериментальной АЧХ для каждой пары максимум – минимум были вычислены коэффициенты отражения и определен усредненный по всей реализации АЧХ │<V>│ = 0,177. Вычисленная по (10) соответствующая условиям рис.10а теоретическая АЧХ атмосферного радиоканала над песчаной поверхностью приведена на рис.10б. Для указанных выше параметров геометрической схемы эксперимента полоса частот данного радиоканала составила около 1 ГГц.
Рис.10. Фрагмент записи (реализации) частотной характеристики атмосферного радиоканала над песчаной подстилающей поверхностью (А) и теоретическая АЧХ для эффективного коэффициента отражения |V|= 0,177 (Б)
Заключение
Рассмотрены различные факторы, влияющие на условия распространения ММВ в приземном слое атмосферы, а именно молекулярное поглощение в атмосферных газах, рассеяние в гидрометеорах, искривление траекторий из-за рефракции, флуктуации из-за турбулентности, отражение от подстилающей поверхности.
Развитый теоретический подход к описанию спектров газов, основанный на использовании метода функций памяти и моделей обобщенной вращательной диффузии, позволяет получать более полную и точную исходную спектроскопическую информации о газах для интерпретации дистанционных измерений, оценок ослабления излучения, моделирования радиационного переноса. Решен ряд задач по дальнейшему развитию способов качественного и количественного спектрального анализа состава газовых сред. Большую роль в этом играет задача интерпретации спектров, связанная с вопросами исследования строения молекул, их пространственной структуры, характера межмолекулярных движений и взаимодействий в газах. Такая связь объясняется тем, что расчеты макроскопических характеристик газов (например, комплексной диэлектрической проницаемости) основываются на микроскопическом рассмотрении динамических процессов в газах. Все эти прикладные аспекты, свидетельствующие о важности исследования дисперсии и поглощения электромагнитных волн ММ и СММ диапазона в полярных газах, нашли широкое освещение в публикациях ИРЭ РАН. Важным моментом предложенного теоретического подхода является применимость его не только для полярных газов, но и в случае растворов полярных жидкостей и жидких кристаллов.
Расчеты коэффициентов ослабления и рассеяния радиоволн в дожде показывают, что ослабление миллиметровых волн в дожде в равной степени обусловлено как поглощением энергии волны в объеме капель, так и дифракционным рассеянием падающей волны на каплях, причем это соотношение (между поглощением и рассеянием) практически не зависит ни от длины волны (в диапазоне ММВ), ни от интенсивности дождя, ни от спектра размеров капель. В диапазоне СМ волн, напротив, ослабление определяется, главным образом, поглощением, а роль рассеяния падает с увеличением длины волны, с уменьшением интенсивности дождя и зависит от вида распределения капель по размерам.
В отличие от релеевской индикатрисы рассеяния СМ волн в осадках, которая мало зависит от длины волны излучения, интенсивности дождя и распределения капель по размерам, индикатриса рассеяния ММВ в дожде демонстрирует ярко выраженный эффект Ми.
Разработан алгоритм, позволяющий находить траектории, связывающие источник и приемник излучения при любых заданных как их координатах, так и вертикальных профилях коэффициента преломления. Этот алгоритм, состоящий из компактных выражений, приспособлен для численных расчетов на ЭВМ и пригоден также и для случаев многолучевого распространения, когда конечные пункты могут быть связаны несколькими траекториями. Численное моделирование распространения в приземном слое выполнено для трассы, параметры которой близки к экспериментальной. Обнаружено качественное согласие характера отклонений видимого угла прихода, рассчитанных по измерениям веритикальных профилей атмосферы с измеренными. Расчеты показывают, что на приземной трассе возможно не только отсутствие связи, но и возникновение многолучевости, обусловленной только особенностями преломления в атмосфере.
В результате расчетов статистических характеристик флуктуаций амплитуды и фазы поля в приземном слое турбулентной атмосферы показано, что:
- средний квадрат уровня амплитуды
![]() пучка ММВ зависит лишь от длины волны и протяженности
трассы и не зависит от размеров пучка;
пучка ММВ зависит лишь от длины волны и протяженности
трассы и не зависит от размеров пучка;
- среднеквадратичные флуктуации амплитуды пучка ММВ в 1,8 раза меньше, чем для плоской волны;
- среднеквадратичные флуктуации направления распространения пучка ММВ в случае точечного приемника определяются не внутренним масштабом турбулентности, как в случае плоской монохроматической волны, а эффективным начальным радиусом пучка re.
Установлено, что поглощение в ММ и СБММ диапазоне не оказывает существенного влияния на интенсивность флуктуаций амплитуды, фазы и направления распространения пучка ММВ – его влияние составляет доли процента даже вблизи линий поглощения
В течение двух лет на приземной трассе параллельно проведены две серии экспериментов по исследованию как флуктуаций интенсивности и угла прихода, обусловленных атмосферной турбулентностью, так и рефракции, вызванной вертикальной стратификацией приземного слоя. Изучение спектрального состава флуктуаций показало, что в области частот, соответствующих инерционному интервалу турбулентности (порядка 0,1 Гц и выше) усредненный наклон спектров составляет –2,2, в то время как его теоретическое значение равно –2,67. В низкочастотной области (менее 0,1 Гц), которая не описывается теоретически, отмечается существенное отличие спектров для вертикальной и горизонтальной составляющих угла прихода, которое свидетельствует о возрастании степени анизотропии турбулентности с уменьшением пространственной частоты турбулентных неоднородностей.
Данных по температуре, влажности, давлению воздуха, скорости и направления ветра в приземном слое недостаточно для точного теоретического прогнозирования параметров ММ волн. Необходимы еще и данные по вертикальной стратификации, уровню и анизотропии турбулентности на высотах ПСА. К настоящему времени такие атмосферные модели не созданы. Необходимо развивать и методы расчета, использующие неизотропные модели турбулентности, зависящие от высоты над земной поверхностью.
В результате экспериментальных исследований при высотах корреспондирующих пунктов 10 – 15 м подтверждено наличие интерференционной структуры поля, которая сохраняется и на трассах, протяженностью несколько километров.
Показано, что при отражении от слабошероховатой поверхности для трассы, описанной в п. 6, полоса пропускания атмосферного радиоканала длиной несколько километров составляет ~ 1000 МГц.
Авторы выражают искреннюю признательность и благодарность участникам отдельных этапов этого исследования – Г. А. Андрееву, Б. А. Розанову, И. Н. Фетисову, Г. Н. Соловьеву, Ю. П. Калмыкову, В. А. Паршукову, C. А. Огареву, А. Н. Горбовой, З. А. Мартыновой, Е. П. Новичихину за помощь в выполнении экспериментальных и теоретических этапов и за удовольствие от общения в процессе работы.
Литература
1. Kalmykov Yu. P,. Titov S. V. A Semiclassical Theory of Dielectric Relaxation and Absorption in Polar Fluids: Memory Function Approach to the Extended Rotational Diffusion Models. - Relaxation Phenomena in Condensed Matter, Ed. W.T.Coffey, Advances in Chemical Physics, Series Editors I.Prigogine and S.A.Rice, Wiley, New York, 1994, v. 87, p. 31-122.
2. Калмыков Ю.П, Титов С.В. Молекулярное поглощение миллиметровых и субмиллиметровых волн в атмосферном кислороде и водяном паре. - Электромагнитные волны и электронные системы, 1997, т.2, N 4, с.80-86.
3. Калмыков Ю.П, Титов С.В. Обобщенная вращательная диффузия и молекулярное поглощение в газах: метод функций памяти. - Зарубежная радиоэлектроника, 1998, N 9, с.32-50.
4. Калмыков Ю.П, Титов С.В. Обобщенная вращательная диффузия с учетом конечной длительности соударений: полуклассическая теория. - Оптика и спектроскопия, 1995, т.79, N 6, с.929-935.
5. Калмыков Ю.П, Новскова Т.А., Титов С.В. Спектр поглощения молекулярного кислорода в диапазоне частот 50-70ГГц: уширение давлением в рамках модели J-диффузии. - Радиотехника и электроника, 1998, т.43, N 5, с. 613-621.
6. Калмыков Ю.П., Титов С.В. Применение метода функций памяти для расчета вращательного спектра поглощения паров воды. - Препринт ИРЭ АН СССР, N 14(473), 1987.
7. Калмыков Ю.П., Титов С.В. Использование модели J-диффузии Гордона для расчета 0-ТГц спектра поглощения молекулярного кислорода. – Тез. докл. 20 Всес. съезда. по спектроскопии. - Киев, 1988, т.1, с.257.
8. Титов С.В. Комплексная диэлектрическая проницаемость полярных газов в диапазоне частот 0-1ТГц. Метод функций памяти. – Диссертация на соискание ученой степени канд. физ.-мат. наук, 1989, М., МФТИ, 188 с.
9. Калмыков Ю.П, Титов С.В. Применение метода функций памяти для расчета вращательного спектра поглощения паров воды. - Радиотехника и электроника, 1989, т.34, N 1, с.13-20.
10. Калмыков Ю.П, Титов С.В. О спектре поглощения молекулярного кислорода в 0-ТГц диапазоне частот. – Изв. ВУЗов, Радиофизика, 1989, т.32, N 8, с.933-944.
11. Калмыков Ю.П, Титов С.В. K теории поглощения микроволнового излучения молекулярным кислородом. - Тез. докладов 3 Всес. школы по распространению мм и СБММ волн в атмосфере. - Харьков, 1989, с.39-40.
12. Калмыков Ю.П, Титов С.В. Модель молекулярнного поглощения миллиметровых и субмиллиметровых радиоволн в атмосферных парах воды. Тез. докладов 3 Всес. школы по распространению ММ и CБММ волн атмосфере. - Харьков, 1989, с.38.
13. Калмыков Ю.П, Титов С.В. К теории молекулярного поглощения сантиметровых и миллиметровых волн в кислороде. - Радиотехника и электроника, 1991, т.36, N 12, с.2281-2290.
14. Калмыков Ю.П, Титов С.В. О форме линии поглощения вращательных спектров полярных газов в приближении моделей сильных столкновений. - Оптика и спектроскопия, 1992, т.72, N 1, с.49-55.
15. Калмыков Ю.П., Титов С.В. Квантовая дипольная автокорреляционная функция модели свободного вращения. - Радиотехника и электроника, 1987, т.32, N 9, с.1902-1908.
16. Калмыков Ю.П, Титов С.В. О поглощении миллиметровых и субмиллиметровых радиоволн в водяном паре. - Оптика и спектроскопия, 1993, т.75, N 3, с.610-616.
17. Гайдук В.И., Титов С.В. Квантовая система линейных молекул при произвольном наборе времен релаксаций и вращательные спектры газоподобных жидкостей. - Препринт ИРЭ АН СССР, N 3 (504), 1989.
18. Гайдук В.И., Титов С.В. Приближенное описание квантовой системы линейных молекул при произвольном наборе времен релаксаций и вращательные спектры газоподобных жидкостей. - Оптика и спектроскопия, 1990, т.68, N5, с.1043-1049.
19. Калмыков Ю.П, Титов С.В. Комплексная проницаемость полярных газов в приближении сильных столкновений: метод функций памяти. Тез. докладов 4 Всес. школа по распространению ММ и СБММ волн в атмосфере. - Ниж. Новгород, 1991, с.37-38.
20. Калмыков Ю.П, Титов С.В. Диэлектрическая восприимчивость полярных сред в приближении сильных столкновений при произвольной зависимости частоты столкновений от вращательной энергии молекул. - Химическая физика, 1992, т.11, N 12, с.1612-1619.
21. Калмыков Ю.П, Титов С.В. Комплексная восприимчивость полярных газов в приближении сильных столкновений: метод функций памяти. - Оптика и спектроскопия, 1993, т.75, N 2, с.266-275.
22. Калмыков Ю.П, Титов С.В. Диэлектрическая релаксация и обобщенная вращательная диффузия молекул типа асимметричного волчка с учетом конечной длительности столкновений. - Химическая физика, 1998, т.17, N 12, с.116-128.
23. Kalmykov Yu. P,. Titov S. V. Absorption spectrum of molecular oxygen in 50-70 GHz frequency band: J-diffusion model. J.Communications Technology and Electronics, 1998, v.43, N 5, р 565-573.
24. Kalmykov Yu. P,. Titov S. V. Dielectric relaxation and extended rotational diffusion of asymmetric top molecules with account of finite duration of collisions. - J.Molecular Structure, 1999, v. 479, p. 123-133.
25. Kalmykov Yu. P,. Titov S. V. Dielectric relaxation and a generalized model of rotational diffusion of asymmetric-top molecules with regard for finite collision time. - Chem.Phys.Reports, 1999, v.17, N 12, p.2371-2388.
26. Kalmykov Yu. P,. Titov S. V. Extended rotational diffusion of asymmetric top molecules with account of finite duration of collisions, - Proc. 4th Liquid Matter Conf.,Granada, Spain, 1999, P1/34.
27. Kalmykov Yu. P.,. Perova T.S, Faurskov Nielsen J.K. Vij, O.,. Titov S. V. Far-infrared and low frequency Raman spectroscopy of orientational relaxation of polar liquids. - Proc. 4th Liquid Matter Conf.,Granada, Spain, 1999, P2/36.
28. Калмыков Ю.П, Титов С.В. Спектральные моменты и ориентационные корреляционные функции молекул типа асимметричного волчка. - Оптика и спектроскопия, 2000, т.89, N 1, с.29-36.
29. Pardoe G.W.F., Gebbie H.A.. Symposium on submillimeter waves. Brooklyn: Polytechnic Inst. 1970. р.643.
30. Шифрин К.С. Рассеяние света в мутной среде. - М.-Л., ГТИ, 1951, 430 с.
31. Ван де Хюлст. Рассеяние света малыми частицами. - М., ИЛ, 1961, 536 с.
32. Борен К.,.Хафлен Д. Поглощение и рассеяние света малыми частицами. - М., "Мир", 1986, 660 с.
33. Огути Т. Распространение и рассеяние электромагнитных волн в дожде и других гидрометеорах. - ТИИЭР, 1983, т. 71, N 9, с. 6-65.
34. Кутуза Б.Г, Загорин Г.К, Спектральные и поляризационные свойства ослабления и издучения осадков в миллиметровом диапазоне волн. - Сб. тез. докл. на школе-семинаре в Красновидово. Май 2000 г.
35. Загорин Г.К, Соколов. А.В. Поляризационные эффекты при распространении миллиметровых радиоволн в осадках. – Тез. лекций и докл. II Всес. школы-симпозиума по распространению миллиметровых и субмиллиметровых волн в атмосфере (под ред. проф. А.В.Соколова). - Фрунзе, "Илим", 1986, с. 157-167.
36. Загорин Г.К., Кутуза Б.Г. Особенности переноса поляризованного теплового СВЧ излучения в облаках и осадках. - Радиотехника, 1998, вып. 10, с. 21-31.
37. Дейрменджан Д, Рассеяние электромагнитного излучения сферическими полидисперсными частицами. - М., "Мир", 1971, 165 с.
38. Mie G. Beitrage zur optik truber medien speziel kolloidaler metallosungen. - Annalen Physik, 1908, v. 25, N 4, p. 377-445.
39. Загорин Г.К, Соколов. А.В. Сухонин Е.В. Взаимные помехи между радиосистемами при рассеянии радиоволн в дождях. - Труды I Всес. школы-симпозиума по распространению миллиметровых и субмиллиметровых волн в атмосфере. (10-17 февраля 1982), - М., 1983, с. 129-134.
40. Загорин Г.К, Соколов. А.В. Методика аналитических оценок уровня взаимных помех между радиоэлектронными системами из-за рассеяния радиоволн в дожде. - Труды IХ International Wroclaw Symposium on Electromagnetic Compatibility. June 28-30, 1988, pt.2, p.583-588.
41. Загорин Г.К, Соколов. А.В.. Многократное рассеяние миллиметрового излучения круговой поляризации в дожде. - В Сб. Электромагнитные волны в атмосфере и космическом пространстве. (Под ред. проф. А.В. Соколова и проф. А.А. Семенова) М., "Наука", 1986, с. 75-82.
42. Волчок Б.А., Черняк М.М. Перенос микроволнового излучения в облаках и осадках. - Труды ГГО, Л., Гидрометеоиздат, 1968, вып. 222, с. 83.
43. Загорин Г.К, Соколов. А.В. Радиотепловое излучение миллиметровых волн в дожде. – Тез. докл. XIV Всес. конф. по распространению радиоволн. (Ленинград 1984). М., "Наука", 1984, ч. 2, с. 19-21.
44. Загорин Г.К, Поляризационные характеристики (параметры Стокса) собственного и рассеянного СВЧ излучения в дожде. - Дис. на соискание ученой степени канд. Физ.-мат. наук, ИРЭ РАН, Москва, 1998 г.
45. Паршуков В.А., Зражевский А.Ю., Новичихин Е.П. Алгоритм расчета траекторных параметров электромагнитных волн в сферически-слоистой атмосфере. - Радиотехника и электроника. 1994, т. 39, № 6, , c. 915-922.
46. Зражевский А.Ю., Методика расчета поглощения в атмосферных парах воды в ММ и СБММ диапазонах. - Радиотехника и электроника, 1976, т.21, №5, с. 951-957.
47. Зражевский А.Ю., Малинкин В.Г. Инженерный метод расчета вращательной части диэлектрической проницаемости водяного пара для l³0,33 мм. - Радиотехника и электроника, , 1977, т.ХХ11, N 1, c. 176-178.
48. Зражевский А.Ю., Малинкин А.В., Соколов А.В. - Радиотехника и электроника ,1974, т. 19, N 11, с. 2392.
49. Розанов Б.А., Фетисов И.Н., Зражевский А.Ю., Коньков Е.В. Исследования распространения миллиметровых радиоволн в приземном слое атмосферы, - Вестник МГТУ, Серия "Приборостроение", 1990, N 1, с.60-66.
50. Зражевский А.Ю., Новичихин Е.П.,.Паршуков В.А., Рукина А.Н., Влияние условий приземного слоя на рефракцию ММ и оптических волн. - Труды 2 Всес. Школа-симпозиума по распространению ММ и СБММ волн в атмосфере, Фрунзе, Илим, 1986,с. 46-48.
51. Паршуков В.А., Зражевский А.Ю., Горбова А.Н. Годовая статистика траекторных параметров миллиметровых и оптических волн на приземной трассе. - Радиотехника и электроника, 1996, т. 41, N 9, с.1039-1044.
52. Паршуков В.А., Зражевский А.Ю., Новичихин Е.П., Мартынова З.А., Траектории радиоволн на приземных трассах в реальной атмосфере. - Электромагнитные волны и электронные системы, 1997, т. 2, N 3, с.66-70.
53. Паршуков В.А. Оценка влияния ошибок метеоизмерений на результаты расчета траекторных параметров радио- и оптических волн в приземном слое. - Радиотехника и электроника, 1998, т. 43, N 2, c.148-152.
54. Иванов В.Н, Паршуков В.А. и др. Учет радиорефракции при наблюдении Солнца вблизи горизонта. - Труды ХХУ Радиоастрономической конф. Пущино, 1993, с. 250-251.
55. Иванов В.Н, Паршуков В.А. и др. О возможности прогнозирования и компенсации астрономической рефракции вблизи горизонта. – Труды 3 Всес. Школа по распространению ММ и СБММ волн в атмосфере. Тез. докл. Н.Новгород, 1991,с.53.
56.Татарский В.И. Распространение волн в турбулентной атмосфере. - М., "Наука", 1967.
57.Исимару А. Распространение и рассеяние волн в случайно-неоднородных средах. - М., "Мир", 1981, ч. 2.
58. Андреев Г.А., Черная Л.Ф. Флуктуации пучка миллиметровых волн в турбулентной поглощающей тропосфере Земли. - Радиотехника, 1978, т. 33, N 1, с.16-29.
59. Черная Л.Ф. "Влияние хаотических неровностей земных покровов на распространение миллиметровых волн". – Дис. на соискание ученой степени канд. физ.-мат. наук. М., 1984
60. Андреев Г.А., Зражевский А.Ю., Изюмов А.О., Малинкин В.Г. Структурные характеристики показателя преломления турбулентной поглощающей атмосфере в субмиллиметровом диапазоне волн. - Препринт ИРЭ РАН СССР N 28(117), М., 1974, 12 с.
61. Мясин Е.А., Черная Л.Ф., Жаркова Н.В., Загорин Г.К, Коньков Е.В., Котов В.Д., Розанов Б.А., Титов С.В.. Исследование распространения широкополосных сигналов миллиметрового диапазона в приземном слое атмосферы и определение на этой основе ограничений, накладываемых на предельно достижимые характеристики локационных систем с шумовыми и широкополосными сигналами. – Сб. отчетов по научным проектам МНТП России "Физика микроволн", 1999, т.1, Нижний Новгород, с. 132-138.
62. Коньков Е.В., Амплитудные и фазовые характеристики миллиметровых радиоволн в приземном слое атмосферы, - Дис. на соискание ученой степени канд. физ.-мат. наук, Москва, ИРЭ АН СССР, 1990.
63. Konkov E.V., Zrazhevsky A.U., Solovev G.N. Investigations of the Near-Millimeter-Wave propagation on the surface boundary layer path, Int. Journal of Infrared and Millimeter Waves, v. 13, N.7, 1992, p. 955-969.
64. Konkov E.V., Zrazhevsky A.U., Angle-of-Arrival variations of millimeter waves on the terrestrial path, XXIV-th General Assembly of URSI, Kyoto, Japan, Aug.25-Sept.2, 1993, p.233.
65. Коньков Е.В., Зражевский А.Ю., Соловьев Г.Н. Влияние атмосферной рефракции на точность пеленга цели в коротковолновой части миллиметрового диапазона, - Электромагнитные волны и электронные системы, 1997, N1, т.2, с.72-76.
66. Коньков Е.В., Зражевский А.Ю., Соловьев Г.Н. Флуктуации интенсивности и угла прихода миллиметровых радиоволн на приземной трассе, - Электромагнитные волны и электронные системы, 1997, N 4, т.2, с. 877-882.
67. Кугушев А.М., Калачев П.Д., Парщиков А.А., Розанов Б.А., Фетисов И.Н. Антенны РТ-7,5 радиотелескопа миллиметровых волн МВТУ, - Сб. "Антенны", М.: Сов. Радио, 1980, вып.28, с. 3-12.
68. Розанов Б.А. Радиотелескоп ММ диапазона РТ-7,5 МВТУ,- Изв. Вузов СССР, сер. Радиоэлектроника, 1981, N 3, т. 24, с. 3-8.
69. Розанов Б.А., Жаркова Н.А., Михайлицкий В.П. Супергетеродинные радиометры миллиметрового диапазона с амплитудной и диаграммной модуляцией, - Тез. докл., 3-й Всес. Симпозиум по ММ и СБММ волнам, Горький, 1980, т.1, с. 169.
70 Казаков Л.Я., Ломакин А.Н. Неоднородности коэффициента преломления воздуха в тропосфере, - М.: Связь, 1976.
71. Propagation of short radio waves..Ed/ D/F/ Kerr., N.Y. Mc Grow-Hill, 1951, 792 p. (MTT Radiat. Lab. Ser., v. 13).
72. Аренберг А.Г. Распространение дециметровых и сантиметровых радиоволн. М., "Сов. Радио", 1957, 300 с.
73. Фейнберг Е.Л. Распространение радиоволн вдоль земной поверхности. М., Изд. АН СССР, 1961, 545 с.
74. Басс Ф.Г., Фукс И.М. Рассеяние радиоволн на статистически неровной поверхности. - М., "Наука", 1972, 424 с.
75. Андреев Г.А., Мартынова З.А., Хохлов Г.И. Влияние отражения подстилающей поверхности на прием ММВ. Радиотехника, 1979, т. 34, N 8, с. 73-74.
76. Андреев Г.А., Огарев С.А., Хохлов Г.И. Частотные характеристики в миллиметровом диапазоне волн турбулентного тропосферного радиоканала над хаотической подстилающей поверхностью. - Радиотехника и электроника, 1994, т. 39, N 11, с.1741-1750.
77. Андреев Г.А. , Хохлов Г.И., Черная Л.Ф. Влияние подстилающей поверхности на распространение миллиметровых волн в атмосфере. - В кн. Электромагнитные волны в атмосфере и космическом пространстве, М., Наука, 1986г.
78. Андреев Г.А. - Тез. докл. 3 Всес. школы по распространению ММ и СБММ волн в атмосфере, Харьков, октябрь 1989, Харьков, ИРЭ АН УССР 1989, с.167.
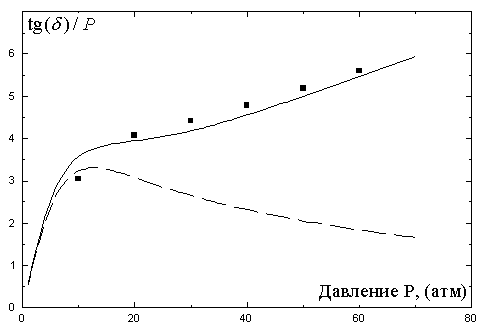

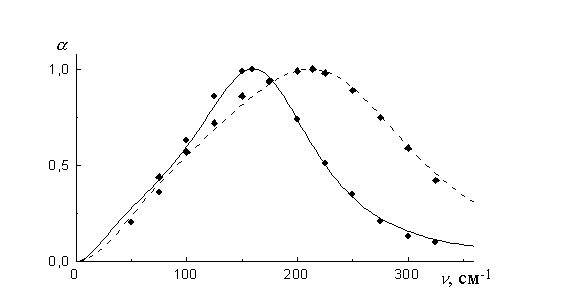
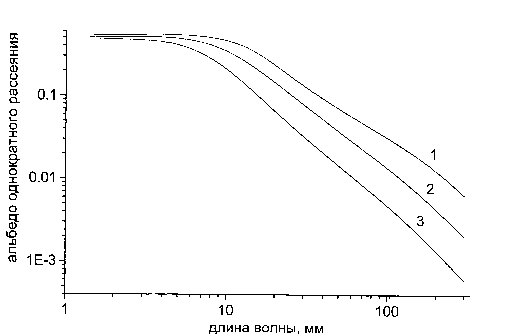
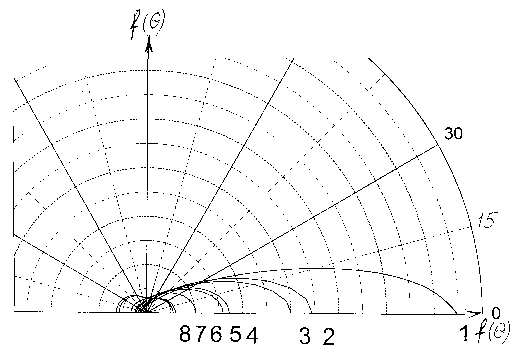
 ,
, 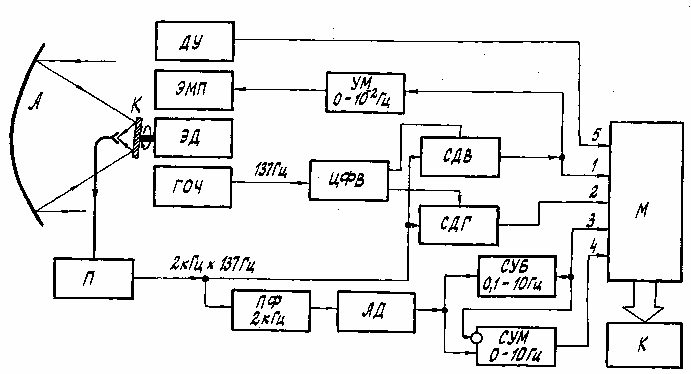
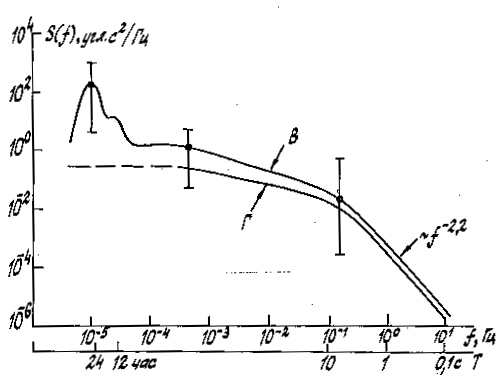
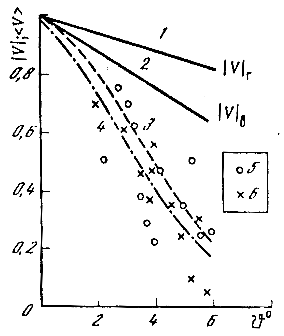
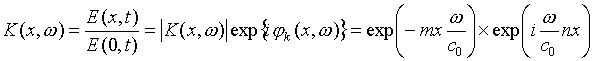
 . (10)
. (10)