|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 8, 2004 |
|
СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В ЗАДАЧАХ РАВНОМЕРНОЙ ОПТИМИЗАЦИИ
ПОИСКА СТОХАСТИЧЕСКОЙ ЦЕЛИ
А. А. Строцев
Ростовский военный институт ракетных войск
Получена 27 июля 2003 г.
В статье рассмотрен вопрос применимости статистического моделирования при синтезе равномерно оптимального управления поиском в большой поисковой системе, в случае, когда движение цели описывается стохастическими дифференциальными уравнениями.
Особенность равномерно оптимальных стратегий поиска связано с тем, что их применение приводит к реализации оптимального поиска в быстро меняющейся обстановке практически в каждый момент времени. В [1], [2] рассмотрены задачи синтеза равномерно оптимальных стратегий поиска неподвижных и условно детерминированных целей многопозиционной информационной системой (большой поисковой системой). Однако в виду влияния случайных факторов реальное движение цели в каждый момент времени носит стохастический характер. Получение условий оптимальности поиска таких целей на основе подхода Егорова [3] рассмотрено, например, в [4]. При этом оптимизационная задача сводится к краевой с движущейся границей, осложнённой тем, что граница области отличных от «0» значений оптимальной стратегии поиска является одной из неизвестных функций. Решение этой задачи связано с большими вычислительными и теоретическими трудностями.
С другой стороны для решения сложных задач в различных областях науки и техники разработан универсальный метод статистического моделирования [5], [6]. И хотя его применение требует проведения большого числа испытаний для достижения заданной точности результата в связи со значительным ростом вычислительной мощности современных ЭВМ актуальность статистического моделирования неуклонно возрастает [7]. Кроме того, разработаны и продолжают совершенствоваться методы ускоренного статистического моделирования [8], обеспечивающие сокращение затрат машинного времени в 2 - 6 раз по сравнению со статистическим моделированием по обычной схеме метода Монте-Карло при той же точности оценки.
Таким образом, синтез равномерно оптимального управления поиском стохастической цели на основе статистического моделирования является актуальной задачей.
Рассматривается большая поисковая система, действия отдельных поисковых
единиц которой описываются функцией плотности поиска (стратегией поиска) ![]() ,
, ![]() [4].
[4].
![]() - область поиска,
- область поиска, ![]() ,
, ![]() - известная функция,
- известная функция, ![]() - есть вероятность
обнаружения цели в интервале времени
- есть вероятность
обнаружения цели в интервале времени ![]() при условии, что цель находится в
некоторой небольшой области
при условии, что цель находится в
некоторой небольшой области ![]() точки
точки ![]() и не обнаружена до момента
и не обнаружена до момента ![]() .
.
Положение новой цели в области поиска ![]() задаётся начальной плотностью
распределения
задаётся начальной плотностью
распределения ![]() . Движение цели описывается
векторным стохастическим дифференциальным уравнением
. Движение цели описывается
векторным стохастическим дифференциальным уравнением
где ![]() ,
,
![]()
- случайная функция времени
- случайная функция времени ![]() с заданными статистическими свойствами,
с заданными статистическими свойствами, ![]() .
.
Полагается,
что область поиска ![]() ,
динамика цели, описываемая выражением (3), и начальная плотность распределения
положения цели
,
динамика цели, описываемая выражением (3), и начальная плотность распределения
положения цели ![]() таковы, что
таковы, что 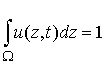 для всех
для всех ![]() .
.
Требуется обосновать применение статистического моделирования при синтезе
равномерно оптимальной стратегии поиска для задачи (1)-(3) по критерию минимума
вероятности ![]() необнаружения
цели к моменту времени
необнаружения
цели к моменту времени ![]() .
.
Сформулируем и докажем основную теорему, обосновывающую применение методов статистического моделирования для оптимизации поиска стохастических целей.
Теорема
Пусть ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() - ограниченные на
- ограниченные на ![]() функции, тогда для функционала
функции, тогда для функционала
справедливо соотношение
где
Доказательство.
Учитывая, что ![]() преобразуем
(4)
преобразуем
(4)
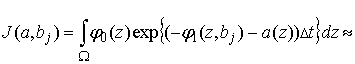
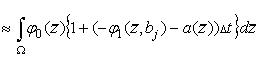 .
.
Тогда


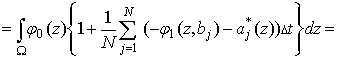
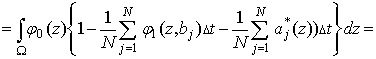
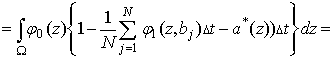
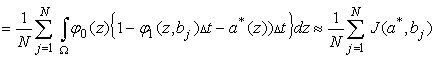 .
.
Т.е.  , откуда, учитывая
, откуда, учитывая
 , следует утверждение
теоремы.
, следует утверждение
теоремы.
4. Применение статистического моделирования в задачах поиска.
Для задачи (1) -
(3) получим уравнение динамики условной плотности распределения вероятностей
положения цели ![]() при
некоторой заданной j-ой реализации
при
некоторой заданной j-ой реализации ![]() случайного процесса
случайного процесса ![]() .
.
Скорость изменения по времени плотности распределения вероятностей
положения цели ![]() для (3)
описывается стохастическим уравнением Лиувилля [9]:
для (3)
описывается стохастическим уравнением Лиувилля [9]:
а влияние
процесса поиска на скорость ![]() изменения
по времени этой плотности распределения в условиях (1),(2), согласно
[4],
определяется выражением
изменения
по времени этой плотности распределения в условиях (1),(2), согласно
[4],
определяется выражением
Тогда из (7),
(8) следует, что уравнение динамики условной плотности распределения
вероятностей положения цели при некоторой заданной реализации ![]() случайного
процесса
случайного
процесса ![]() принимает
вид
принимает
вид
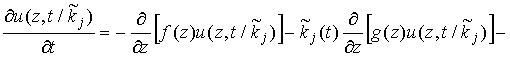
с начальными условиями
Далее, следуя [2], [4], из (9), (10) получим следующую задачу оптимизации с критерием минимума условной вероятности необнаружения цели к моменту времени T:
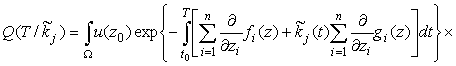
В (11) ![]() - решение (3) при
- решение (3) при ![]() с начальными условиями
с начальными условиями
![]() .
.
Аналогично
[10]
введём понятие ![]() -урезанной
стратегии поиска для задачи (11), (1), (2). Стратегию поиска
-урезанной
стратегии поиска для задачи (11), (1), (2). Стратегию поиска ![]() назовем
назовем ![]() -урезанной, если
-урезанной, если ![]() при
при ![]() . Пусть
. Пусть
Тогда стратегии
![]() ,
, ![]() будут равномерно
оптимальными, если любые соответствующие им
будут равномерно
оптимальными, если любые соответствующие им ![]() -урезанные стратегии будут оптимальны, т.е.
будут выполняться (12), (13).
-урезанные стратегии будут оптимальны, т.е.
будут выполняться (12), (13).
Положим ![]() известными.
Требуется определить
известными.
Требуется определить ![]() ,
где
,
где ![]() .
.
В соответствии с определением равномерно оптимальной стратегии поиска для
любого ![]()
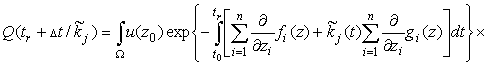
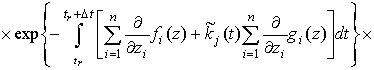
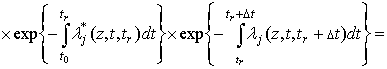
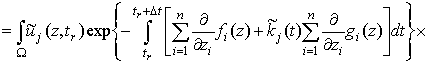
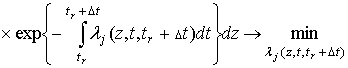 ,
,
где  .
.
Так как ![]() , то получим следующие
оптимизационные задачи
, то получим следующие
оптимизационные задачи
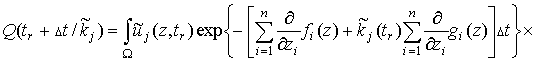
Введём обозначения 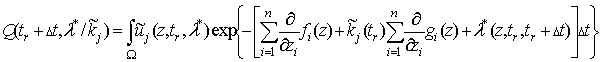 ,
,
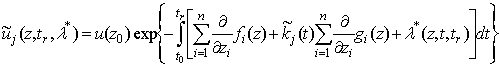 ,
,
тогда на
основании произвольности выбора ![]() и выражений (5), (6), (14) – (18)
справедливо соотношение
и выражений (5), (6), (14) – (18)
справедливо соотношение
Обобщая (19), получим
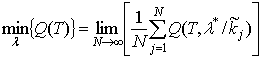 ,
,
где ![]() - оптимальные значения
функционала, а
- оптимальные значения
функционала, а ![]() -
оптимальные решения для задач (11), (1), (2).
-
оптимальные решения для задач (11), (1), (2).
Таким
образом, приближённое решение задачи синтеза равномерно оптимальной стратегии
поиска для (1) - (3) с применением статистического моделирования сводится к
последовательному моделированию случайного процесса ![]() , решению задач
(11), (1), (2) и на основе полученных результатов формированию оценки
, решению задач
(11), (1), (2) и на основе полученных результатов формированию оценки ![]() . Например, при
организации выборочной процедуры в соответствии с методом Монте-Карло
вычисление оценки
. Например, при
организации выборочной процедуры в соответствии с методом Монте-Карло
вычисление оценки ![]() следует
проводить по выражению (20).
следует
проводить по выражению (20).
Отметим, что задачи (11), (1), (2) являются более простыми по сравнению с исходной и их решение рассмотрено, например, в [2], [4].
Специальный вид функционала, используемый при синтезе равномерно оптимальных стратегий поиска стохастических целей, позволяет формировать оценку оптимальной стратегии с применением статистического моделирования на основе решения более простого класса задач – с условно детерминированным движением цели.
Точность полученной оценки определяется значением ![]() и выбором конкретного метода
организации статистического моделирования [8].
и выбором конкретного метода
организации статистического моделирования [8].
1. Строцев А.А. Оптимальный поиск неподвижной цели многопозиционной информационной системой. – Интернет-публикация, М.: Журнал радиоэлектроники , № 4, 2002.
2. Строцев А.А. Оптимизация поиска условно детерминированной динамической цели большой поисковой системой. – Интернет-публикация, М.: Журнал радиоэлектроники , № 12, 2002.
3. Егоров А.И. Необходимые условия оптимальности для систем с распределёнными параметрами. – Математический сборник, 1966, т. 69, №3.
4. Хеллман О. Введение в теорию оптимального поиска. – М.: Наука, 1985.
5. Кокрен У. Методы выборочного исследования. М.: Статистика, 1976.
6. Пугачёв В.Н. Комбинированные методы определения вероятностных характеристик. М.: Советское радио, 1973.
7. Котельников В.П. Компьютерные процедуры для статистических выводов. – Обозрение прикладной и промышленной математики, 1998, т.5, вып. 2.
8. Васильев Д.В., Сабинин О.Ю. Ускоренное статистическое моделирование систем управления. – Л.: Энергоатомиздат. Ленингр. отделение, 1987.
9. Кляцкин В.И. Стохастические уравнения и волны в случайно-неопределённых средах. – М.: Наука, 1980.
10. Аркин В.И. Равномерно-оптимальные стратегии в задачах поиска. – Теория вероятностей и её применения, 1964, т. 9, № 4.
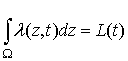 для всех
для всех 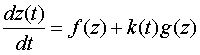
 ,
(4)
,
(4)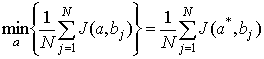 ,
(5)
,
(5)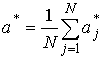 ,
,
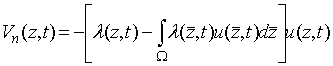
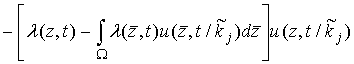 , (9)
, (9)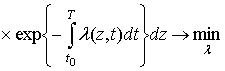
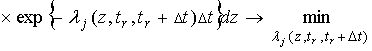 ,
(14)
,
(14)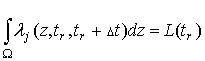 для всех
для всех 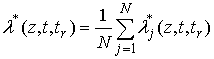 ,
(17)
,
(17)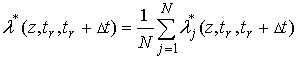 ,
(18)
,
(18)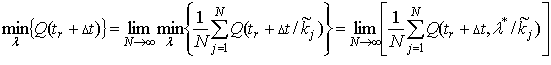 .
.
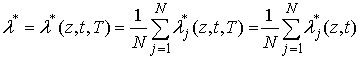 ,
(20)
,
(20)