|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 8, 2007 |
|
УДК 538.566.2;621.371
О ПРЕЛОМЛЕНИИ И ОТРАЖЕНИИИ ВОЛН ПРИЗМОЙ ИЗ МЕТАМАТЕРИАЛА С ПОТЕРЯМИ
Российский Новый Университет, Москва
Получена 9 августа 2007 г.
Приводятся результаты строгих расчетов диаграммы рассеяния гауссова пучка призмой конечных размеров изготовленной из метаматериала с различными значениями показателя преломления
и потерь среды
. Показано, что геометрическая оптика позволяет правильно предсказать отклонение такого пучка , а учет потерь среды при
сказывается на амплитуде прошедшего и отраженного полей.
ВВЕДЕНИЕ
В последнее время наблюдается значительный интерес к эффектам, возникающим при взаимодействии электромагнитных волн со средой, относительная диэлектрическая
и магнитная
проницаемости которой одновременно являются отрицательными величинами (
). Такую среду принято называть средой с отрицательной рефракцией (метаматериалом, средой Веселаго), поскольку впервые задача распространения электромагнитных волн в среде с
была теоретически рассмотрена В.Веселаго еще в 1968 г. [1]. В этой работе он исследовал прохождение плоской гармонической волны через плоский слой среды с
конечной толщины
. При этом, исходя из анализа лучей геометрической оптики (ГО), соответствующей прохождению волны через слой без переотражений на его границах, В. Веселаго сделал ряд необычных предсказаний относительно поведения поля волны, прошедшей через такой слой. В частности, им было указано на то, что плоский слой среды с
позволяет осуществить идеальную (с позиций ГО) фокусировку преломленных и прошедших ГО лучей, когда все прошедшие (преломленные) ГО лучи сходятся в одной точке. Иными словами, плоский слой такой среды преобразует расходящийся фронт падающей цилиндрической волны в сходящийся цилиндрический фронт прошедшей волны. Другой предсказанный эффект был связан с необычным отклонением преломленного луча ГО от нормали к поверхности раздела двух сред, представляющих собой метаматериал и свободное пространство - луч отклоняется в противоположную сторону по отношению к случаю границы раздела обычный диэлектрик и свободное пространство.
Число публикаций, в которых рассматриваются как теоретические, так и экспериментальные аспекты этой проблемы к настоящему времени весьма велико (см. [2-11] и цитируемую там литературу) и все время увеличивается. При этом следует отметить, что во многих работах два подхода – теоретический и экспериментальный, на наш взгляд, не обоснованно противопоставляются друг другу. Хорошо известно, что вплоть до настоящего времени не известны результаты корректно поставленных экспериментов, которые бы противоречили правильно поставленным и решенным численно задачам (строгому численному эксперименту) и наоборот. Из этого следует, что ни один путь не имеет каких либо преимуществ друг перед другом и выбор способа исследования конкретной задачи является делом личного предпочтения исследователя. Поэтому упрекать его в том, что он предпочел тот или иной способ исследования (см. например [10]) не является корректным упреком (или недостатком работы).
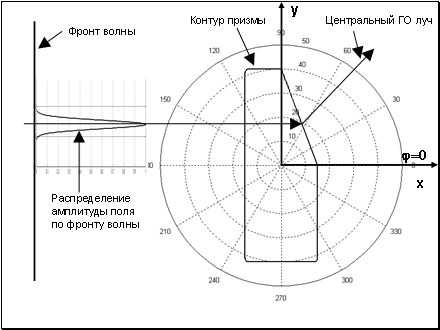
Целью этой работы является дать строгий электродинамический расчет явлений, связанных с преломлением ограниченного пучка волн (например, лазерного пучка) взаимодействующего с призмой состоящей из метаматериала, геометрия которой изображена на Рис.1. Отметим, что экспериментально, такая задача исследовалась в работе [4]. Таким образом, мы, по-видимому, впервые приведем строгие теоретические результаты, подтверждающие влияние отрицательной рефракции на прохождение ограниченного пучка волн через призму. При этом мы покажем, что геометрическая оптика (ГО) позволяет правильно предсказать угол отклонения максимума диаграммы рассеяния в такой призме и его изменение при изменении модуля показателя преломления среды, а учет потерь приводит к изменению амплитуды преломленного и отраженного поля.
ПОСТАНОВКА ЗАДАЧИ И ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Рассмотрим задачу рассеяния волны
, заданной при
декартовой системы координат
в виде гауссова пучка:
двухмерной диэлектрической призмой, форма поперечного сечения
, которой описывается уравнением:
при
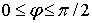
Отметим, что при значения параметра
, контур призмы в полярной системе координат близок к прямоугольнику в области углов
, а при углах
описывается линейной функцией (см. Рис. 1, где приведен рассчитанный контур призмы). Такой выбор формы контура призмы связан с тем, что он позволяет моделировать существенно различные условия преломления пучка волн (1) призмой, меняя значение координаты центра пучка
относительно оси
(
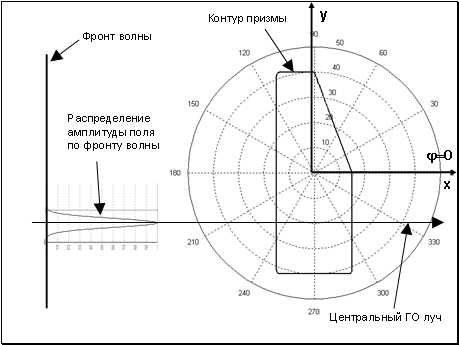
) призмы (см. Рис.1а,б).
а
бРис.1 Геометрия задачи
Считается, что среда пластины имеет относительную диэлектрическую проницаемость
и относительную магнитную проницаемость
одновременно, т.е. представляет собой среду с отрицательным показателем преломления
(где величины :
и
- характеризует показатель преломления и потери среды соответственно).
Входящие в выражения (1), (2) величины представляют собой: {
} – пространственные координаты точки наблюдения в цилиндрической системе координат; величины
- характеризуют геометрию призмы (
- ее высоту,
- ее ширину);
- волновое число вакуума (свободного пространства), соответственно; величины
- определяют первоначальное положение пучка и его эффективную ширину.
Представим полное поле
вне призмы (2) в виде суперпозиции поля падающей волны (1) и рассеянного поля
, а поле внутри пластины (2) обозначим
.
Как известно, поля
и
должны удовлетворять уравнениям Гельмгольца вне и внутри пластины соответственно, а также граничным условиям на контуре
призмы, заключающимся в непрерывности полного поля
и рассеянного поля
, непрерывности их нормальных производных на контуре
и условию излучения на бесконечности (условию Зоммерфельда), т.е. являться решением граничной задачи. Решение такой граничной задачи мы будем строить на основе модифицированного метода дискретных источников (ММДИ) [12-14], который позволяет получить численное решение граничной задачи с контролируемой точностью. Используемое в этом методе представление для полей
,
в виде суперпозиции полей вспомогательных цилиндрических источников, расположенных на вспомогательных контурах внутри и вне контура пластины заведомо удовлетворяет уравнениям Гельмгольца и условию Зоммерфельда. Амплитудные коэффициенты для полей вспомогательных цилиндрических источников в методе ММДИ находятся из условия выполнения граничных условий в
точках контура линзы (2). При этом точность решения задачи определяется невязкой двух граничных условий на контуре призмы и контролируется путем ее вычисления в точках, расположенных в середине между точками, где граничные условия выполняются точно (в таких точках граничные условия выполняются наихудшим образом [12-14]). Поскольку метод ММДИ и техника его применение к ряду задач с аналогичной конфигурацией контура рассеивающего тела описан достаточно подробно в работах [12-14], то мы не будем обсуждать особенности его применения в рассматриваемом случае, а лишь укажем, что при всех расчетах невязка граничных условий
в логарифмическом масштабе вдоль контура призмы не превышала величины
даже при числе вспомогательных источников
и параметрах призмы, указанных ниже.
Обсудим теперь результаты численных расчетов нормированной диаграммы рассеяния
. При расчете нормированной диаграммы рассеяния призмой (2) полагалось, что параметры, характеризующие контур призмы были равны:
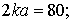
, а показатель преломления
. Таким образом, призма имела скошенную часть, угол наклона которой по отношению к оси
(или
см. Рис.1) был равен
[град.]. Соответственно при этом нормаль
к этой части призмы имела угол наклона
[град.].
Гауссов пучок (1) имел следующие значения параметров
или
. При такой геометрии призмы и параметре пучка
угол падения центрального луча
на скошенную грань призмы был равен
. Следовательно, согласно законам ГО, при показателе преломления
центральный луч ГО должен отклониться в лево от нормали
на угол
, т.е. его общее отклонение от оси
должно составить величину
[град.].
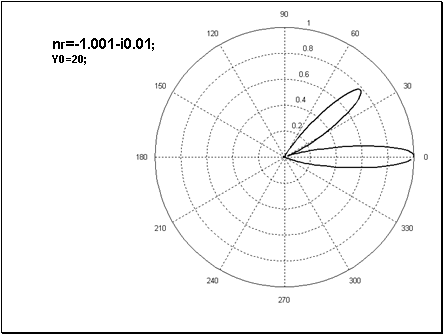
На Рис.2 представлены результаты расчетов нормированной диаграммы рассеяния такой призмой построенные в полярной системе координат. Из рисунка видно, что нормированная диаграмма рассеяния имеет два ярко выраженных лепестка. Первый лепесток имеет максимум в направлении
, а второй лепесток - в направлении
[град.], соответствующем направлению, предсказанному ГО . Поскольку полное поле состоит из поля падающей волны и рассеянного поля, то поле первого лепестка компенсирует поле падающей волны и диаграмма рассеяния полного поля состоит только из одного – второго лепестка с максимумом в направлении
[град.]. Таким образом результаты расчетов задачи рассеяния пучка волн такой призмой (с показателем преломления
) подтверждают предсказанный ГО угол преломления . Отметим, что при координате центра пучка
, т.е. ситуации, когда центральный луч проходит только через прямоугольную часть призмы, эффекта преломления не наблюдается. Это иллюстрируется результатом расчета нормированной диаграммы рассеяния, представленной на Рис.3.
Рис. 2 Нормированная диаграмма рассеяния (случай Рис.1а) для среды линзы с показателем преломления
.
Из результатов, представленных на Рис.2 и Рис.3 так же следует, что такая призма практически не отражает поле в обратном направлении (в области углов
[град.]) поскольку уровень поля в области углов
близко к нулю.
Влияние потерь
и
среды призмы на рассеянное поле иллюстрируют результаты, представленные на Рис.4 и Рис.5 соответственно. Видно, что увеличение потерь в таком диапазоне (
) сначала приводит сначала к уменьшению амплитуды преломленного поля, а затем и к увеличению уровня рассеянного назад поля.
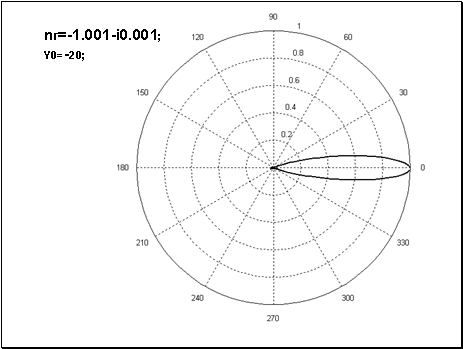
Рис.3 Нормированная диаграмма рассеяния (случай Рис.1б) для среды линзы с показателем преломления
.
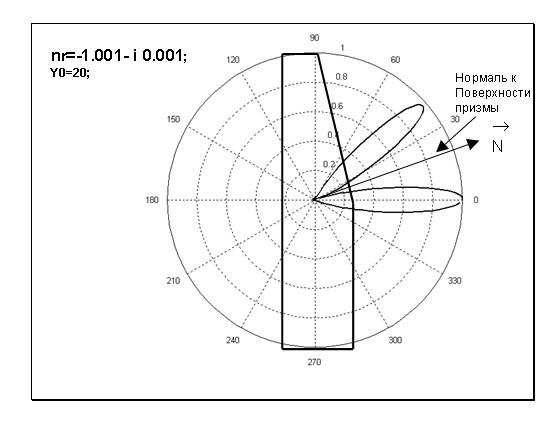
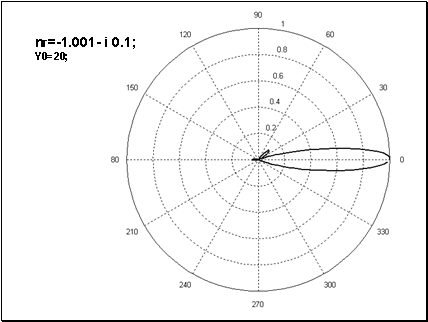
Рис. 4 Нормированная диаграмма рассеяния (случай Рис.1а) для среды линзы с показателем преломления
.
Рис. 5 Нормированная диаграмма рассеяния (случай Рис.1а) для среды линзы с показателем преломления .
.
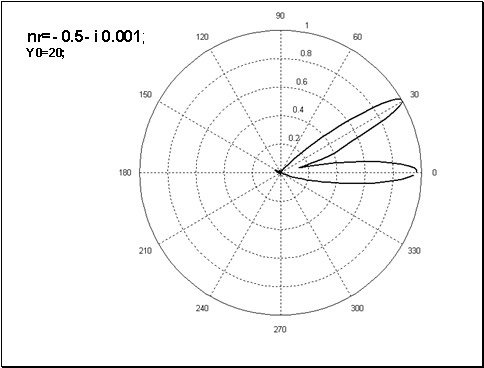
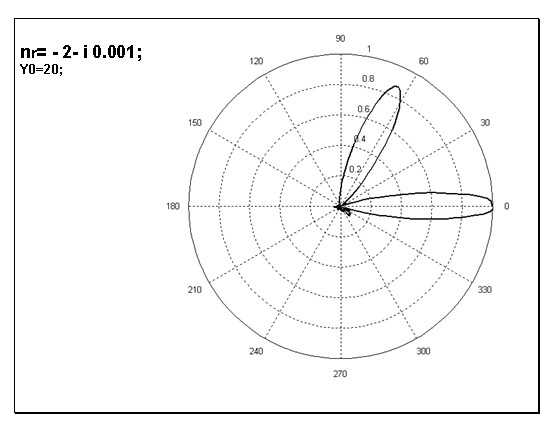
На Рис.6 и Рис.7 изображены нормированные диаграммы рассеяния для призмы, показатель преломления которой был равен
и
соответственно, при этом центра падающего на призму пучка располагался при
, т.е. напротив “скошенной” части призмы . Из рисунков следует, что максимум преломленного поля располагается соответственно при углах
[град.] и
[град.]. К таким же значениям углов преломления приводит и приближение ГО. Отметим появления дополнительного максимума в области углов
[град.] для случая среды с показателем преломления
, который может быть интерпретирован как влияние переотражений на гранях призмы.
Рис. 6 Нормированная диаграмма рассеяния (случай Рис.1а и
)
Рис. 7 Нормированная диаграмма рассеяния (случай Рис.1а и
)
В заключении отметим, что полученные в работе результаты строгого решения задачи рассеяния пучка волн призмой, среда которой представляет собой метаматериал с показателем преломления
, позволяют сделать следующие выводы:
- геометрическая оптика правильно предсказывает положение максимума диаграммы рассеяния призмой, среда которой представляет собой метаматериал с различными значениями показателя преломления;
- учет потерь
такой среды приводит лишь к изменению амплитуды “преломленной” и “отраженной” частей рассеянного поля;
- появление дополнительных максимумов рассеянного поля при показателе преломления
обусловлено влиянием переотражений на гранях призмы.
Работа выполнена при поддержке Российского Фонда Фундаментальных исследований (грант № 06-02-16804, № 06-02-16483).
Литература
1. V.G. Veselago, "Тhe Electrodynamics of Substances with Simultaneously Negative Values of
and
", Sov. Phys. Usp., vol. 10, рр. 509, 1968.
2. Р. Силин,“Possibility of creating plane-parallel lenses ”, Opt. Spectrosc., 44,109,1978
3. D.R. Smith et аl., "Composite Medium with Simultaneously Negative Permeability and Permittivity", Phys. Rev. Lett., vol. 84, р. 4184, 2000.
4. J.B. Pendry and D.R. Smith, "Reversing Light with Negative Refraction", Physics Today, June 2004, рр. 37, 2004.
5. J.B. Pendry, ''Negative Refraction Makes а Perfect Lens", Phys. Rev. Lett., vol. 85, рр. 3966, 2000.
6. GW. 't Hooft, "Comment оп ''Negative Refraction Makes а Perfect Lens"", Phys. Rev. Lett., vol. 87, рр. 249701.1, 2001.
7. George V. Eleftheriades, Ashwin К. Iyer and Peter С. Кremer, “Planar Negative Refractive Index Media Using Periodically L-C Loaded Transmission Lines”, IEEE Tr.MTT,vol.50,N 12, pp. 2702, December 2002
8. В.В Шевченко , “Об обратных плоских волнах в однородных изотропных средах”, РЭ, т.48, N 10, с. 1202, 2003.
9. A.V. Dorofeenko , A.A. Lisyansky , A.M. Merzlikin , A.P. Vinogradov , “Full-wave analysis of imaging by the Pendry-Ramakrishna stackable lens”, Physical Review,
B 73, 235126, 2006 .
10. P.G. Tassin, G. Van der Sande , I. Veretennicoff , “Left-handed materials: the kay to subwavelength resolution?”, Proceedings Symposium IEEE/LEOS Benelux Chapter, Ghent, p.41, 2004.
11. А.П. Анютин, “О расчете поля в области фокуса идеальной линзы Веселаго конечных размеров”, Журнал Радиоэлектроники, N 6 (июнь), 2007.
12. A.P. Anioutine, A.G. Kyurkchan, S.A. Minaev, “About universal modification to the method of discrete sources and its application”, JQSRT, Vol. 79-80, pp.509, 2003
13. А.П. Анютин, А.Г. Кюркчан, С.А. Минаев, “О новой модификации метода дискретных источников”, Радиотехника и Электроника, т.47, N 6, c.688, 2002
14. A.P. Anioutine, A.G. Kyurkchan, S. A. Manenkov, S.A. Minaev, “About 3D solution of diffraction problems by MMDS”, JQSRT, v.100, N1-3, pp.26, 2006 (July/Augest).
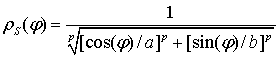 при
при