УДК 621.396.677
СВЕРХРАЗРЕШЕНИЕ ПО ДАЛЬНОСТИ ПРИ ОБРАБОТКЕ РАДИОЛОКАЦИОННЫХ СИГНАЛОВ С ЛИНЕЙНОЙ ЧАСТОТНОЙ МОДУЛЯЦИЕЙ КОГЕРЕНТНЫМ МЕТОДОМ ЛИНЕЙНОГО ПРЕДСКАЗАНИЯ ВПЕРЕД-НАЗАД С ПРОРЕЖИВАНИЕМ ДАННЫХ
Д. С. Григорян 1, С. М. Семченков 2
1лаборатория проблем обработки радиолокационной информации
2 кафедра радиолокационного вооружения военной академии войсковой ПВО
имени маршала Советского Союза А. М. Василевского, Смоленск
Получена 20 июля 2011 г.
Аннотация. С помощью когерентного метода линейного предсказания вперед-назад обработаны спектры моделей эхо сигналов с линейной частотной модуляцией, отраженных от нескольких точечных источников, удаление которых друг от друга меньше ширины релеевского элемента разрешения, определяемого длительностью сжатого импульса. Получены временные функции со сверхразрешением источников по радиальному профилю.
Ключевые слова: сверхразрешение, линейное предсказание, линейная частотная модуляция, вектор весовых коэффициентов, обусловленность, временная функция, спектральная функция, строб дальности.
Abstract. Be founded on weight vector disturbances connection with back-forward linear prediction equations conditionality number the methods of data matrix forming by samples primary processing with coherent accumulation are proposed. By test samples processing the preference of coherent linear prediction with decimation in harmonics superresolution in comparison with primary linear prediction methods is shown.
Keywords: superresolution, linear prediction, weight vector, conditionality, time function.
Введение
В современных радиолокационных системах в настоящее время большое
распространение получили сигналы с линейной частотной модуляцией (ЛЧМ) несущей
частоты, относящиеся к классу широкополосных сигналов, обеспечивающих высокую
разрешающую способность по дальности без уменьшения длительности зондирующих
импульсов [1]. Известно, что длительность ![]() сжатого
сигнала с ЛЧМ длительностью
сжатого
сигнала с ЛЧМ длительностью ![]() обратно
пропорциональна эффективной ширине его спектра [1–4], определяемого девиацией
частоты
обратно
пропорциональна эффективной ширине его спектра [1–4], определяемого девиацией
частоты ![]()
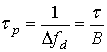 ,
,
где B – база ЛЧМ сигнала. Это свойство объективно вытекает из свойств преобразования Фурье из частотной области во временную область комплексного спектра, ширина которого связана с длительностью временной функции сигнала обратной пропорциональностью. Очевидное достоинство ЛЧМ сигнала это легкость аппаратной реализации широкополосного сигнала путем устройств, обеспечивающих постепенное линейное нарастание частоты. Это позволяет при относительно небольшой пиковой мощности передатчика сконцентрировать в длительном импульсе большую энергию, собираемую в пик сжатого ЛЧМ импульса после его согласованной обработки, что не требует передатчика большой мощности, излучающего короткий импульс.
Необходимость повышения разрешающей способности когерентно-импульсных локаторов приводит к необходимости увеличивать девиацию частоты ЛЧМ радиоимпульсов и прибегать к различным процедурам весовой обработки спектра для уменьшения боковых лепестков сжатых импульсов. Однако ограниченные тактовые частоты (как правило, от 250 – 500 МГц) современных популярных устройств цифровой обработки сигналов (ЦОС) зачастую не позволяют формировать и обрабатывать ЛЧМ импульсы с большой девиацией частоты. Для реализации цифровых когерентно-импульсных и импульсно-доплеровских радиолокаторов с цифровыми фазированными антенными решетками высокие тактовые частоты, определяемые шириной спектра ЛЧМ сигналов, приводят к существенному увеличению объемов информации передаваемой в единицу времени. Это требует использования высокоскоростных микросхем ЦОС в каждом приемо-передающем модуле, что неоправданно повышает стоимость таких систем. Поэтому повышение разрешающей способности ЛЧМ сигналов по дальности сверх элемента разрешения, определяемого длительностью сжатого импульса, на сегодняшнем этапе развития техники ЦОС является актуальной задачей.
Эффект сверхразрешения источников, разность измеряемых параметров которых меньше ширины основного лепестка дискретного преобразования Фурье (ДПФ) выборки, описан во многих работах, среди которых следует отметить известные монографии по классическим методам спектрального оценивания Марпла [5] и Стоицы [6]. Как показывают многие исследования, на которые ссылаются, в том числе, и авторы [5] и [6], сверхразрешение классических методов спектрального анализа достигается, как правило, при больших отношениях «сигнал/шум» (ОСШ). Высокой разрешающей способностью обладают параметрические методы спектрального анализа, основанные на анализе модели авторегресии, коэффициенты которой вычисляются из анализа выборочных оценок корреляционных матриц разными методами (линейное предсказание, ESPRIT, EV, MUSIC и т. д.)
Целью работы является обоснование способа обработки одиночного импульса с линейной частотной модуляцией методом линейного предсказания вперед-назад с когерентным накоплением и прореживанием для сверхразрешения нескольких целей в пределах элемента разрешения по дальности, позволяющего уменьшить порядок модели авторегрессии и улучшить разрешающую способность по сравнению с исходным методом линейного предсказания.
Тестируемая модель сигналов
Рассмотрим модель комплексного прямоугольного ЛЧМ сигнала длительностью τ =50 мкс, девиация частоты которого равна Δfd = 2 МГц. Запишем модель зондирующего сигнала в виде
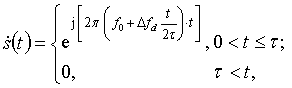
где f0 – несущая частота зондирующего сигнала, определяющая длину волны λ; t – текущее время. На входе приемника сигнал, отраженный от каждого m-го источника можно формально записать в виде
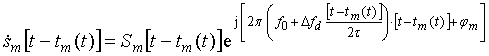 , (1)
, (1)
где
![]() > – время задержки фронта волны, отраженной
от m-го источника;
> – время задержки фронта волны, отраженной
от m-го источника;
![]() – дальность до m-го источника;
– дальность до m-го источника;
![]() ,
, ![]() –
дальность и скорость m-го источника
на момент начала зондирования;
–
дальность и скорость m-го источника
на момент начала зондирования;
![]() – скорость света;
– скорость света;
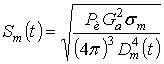 –
амплитудная функция времени;
–
амплитудная функция времени;
![]() –
пиковая мощность зондирующего сигнала;
–
пиковая мощность зондирующего сигнала;
![]() –
коэффициент направленного действия антенны в направлении главного максимума ее
диаграммы направленности;
–
коэффициент направленного действия антенны в направлении главного максимума ее
диаграммы направленности;
![]() –
эффективная поверхность рассеяния m-го
источника;
–
эффективная поверхность рассеяния m-го
источника;
![]() – начальная фаза волны, отраженной от m-го источника;
– начальная фаза волны, отраженной от m-го источника;
Модель сигнала, отраженного от M источников можно представить в виде
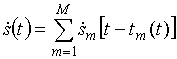 .
.
Как правило, до согласованной обработки ЛЧМ сигнала осуществляется его линейное усиление и неоднократное аналоговое, а затем и цифровое преобразование частоты с помощью DDC (Digital Down Converter) устройств [7] с получением квадратур [7] на нулевой частоте. Считая операции усиления и преобразования ЛЧМ сигналов линейными, n-й отсчет модели цифрового сигнала m-го источника, следующий с интервалом дискретизации по времени Δt после несложных преобразований может быть представлен в виде
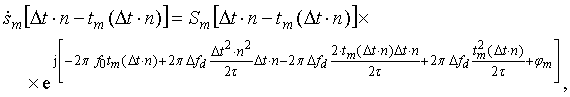 (2)
(2)
а модель дискретного эхо-сигнала от многоточечной цели как
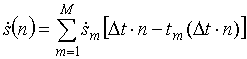 .
.
Обработка ЛЧМ радиоимпульса когерентным методом
линейного предсказания вперед-назад с прореживанием данных
Прежде
чем решать задачу сверхрелеевского разрешения, необходимо сначала обнаружить наличие
сигнала в заданном элементе дальности известными методами. Для примера
рассмотрим стандартную согласованную обработку аддитивной смеси ЛЧМ сигналов
трех источников, второй из которых удален от первого на 30 м, а третий от
первого на 60 м (рис.1). Релеевский элемент разрешения по дальности импульса с
девиацией частоты 2 МГц составляет 75 м (0,5 мкс в сжатом импульсе). Интервал
дискретизации выбран обратно пропорциональным величине девиации, т. е. ![]() .
.
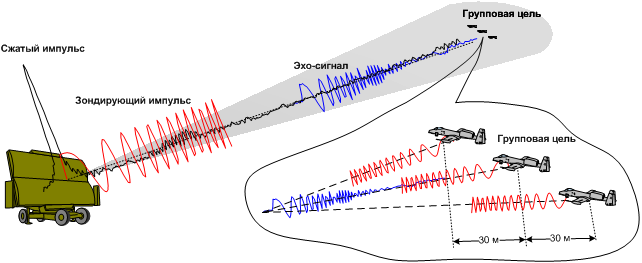
Рис. 1. Моделируемая ситуация зондирования трех целей ЛЧМ импульсом, находящихся на расстоянии 30 м друг от друга.
С целью стандартной согласованной обработки использовалось движущееся окно на N=128 точек (рис.2, кривая 3), отсекающее выборку из 128 отсчетов отраженного сигнала (рис.2, кривая 4). Причем окно смещалось относительно предыдущей позиции через 128 отсчетов.
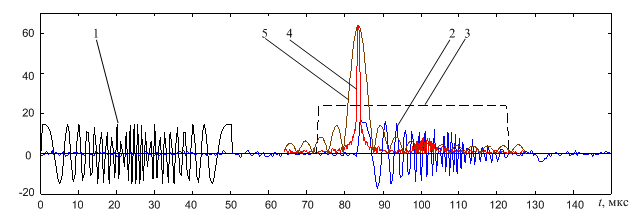
Рис. 2. Вещественные значения комплексных цифровых сигналов:
зондирующий сигнал –1; сигнал, отраженный от трех точечных целей на дальностях 12500 м, 12530 м и 12560 м, движущихся со скоростью 100 м/с в направлении локатора –2; текущее положение движущегося окна –3; модуль сжатого отраженного сигнала –4; (ОСШ для пика сжатого сигнала каждой из целей составляло 36 дБ); временная функция строба дальности, определяемого фильтром предварительной обработки с прямоугольной АЧХ – 5.
К выборке отраженного сигнала, стробированной движущимся окном, применяется операция ДПФ
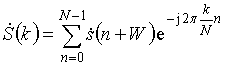 ,
,
где ![]() – номер
отсчета начала движущегося окна; k – индекс частоты (рис.3).
– номер
отсчета начала движущегося окна; k – индекс частоты (рис.3).
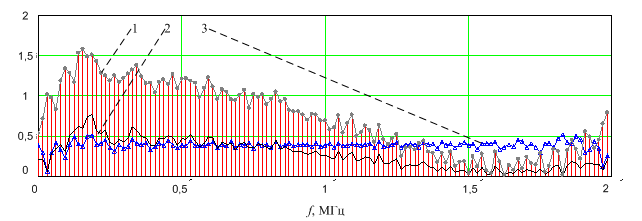
Рис. 3. Модули спектральных функций полученных с помощью ДПФ:
модуль ДПФ сигнала,
отраженного от трех точечных целей на дальностях 12500 м, 12530 м и 12560 м
–1;
модуль сжатого отраженного сигнала –2; АЧХ согласованного фильтра– 3.
Умножая k-е значения ДПФ выборки ![]() (рис. 3, кривая 1) на k-е
значения ДПФ (рис.3, кривая 2)
(рис. 3, кривая 1) на k-е
значения ДПФ (рис.3, кривая 2)
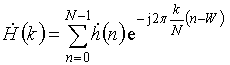
импульсной характеристики согласованного
фильтра ![]() , являющейся комплексно-сопряженной копией
зондирующего сигнала, получим спектр (рис.3, кривая 3)
, являющейся комплексно-сопряженной копией
зондирующего сигнала, получим спектр (рис.3, кривая 3) ![]() ,
обратный ДПФ
,
обратный ДПФ
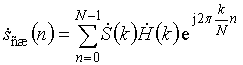
которого даст временную функцию сжатого сигнала (рис. 2, кривая 4). Как видно из рисунка 2 по отклику согласованного фильтра ЛЧМ сигнала цели не разрешаются, так как находятся в пределах релеевского элемента разрешения, то есть разность радиальных расстояний не превышает величины 75 м.
Обнаружив сжатый сигнал
по превышению установленного порога его пиком, перейдем к спектральной
обработке когерентным методом линейного предсказания с прореживанием. Для этого
разобьем выборку из 128 отсчетов ДПФ (спектра) сжатого сигнала ![]() на Q=8 (q=0..Q-1) субвыборок по N1=16 отсчетов (рис.4). Когерентно просуммируем N1 комплексных отсчетов субвыборок ДПФ
на Q=8 (q=0..Q-1) субвыборок по N1=16 отсчетов (рис.4). Когерентно просуммируем N1 комплексных отсчетов субвыборок ДПФ ![]() по частотному индексу k, предварительно умножая их на
комплексные значения фильтра с прямоугольной АЧХ, КЧХ которого представляет
комплексную экспоненту
по частотному индексу k, предварительно умножая их на
комплексные значения фильтра с прямоугольной АЧХ, КЧХ которого представляет
комплексную экспоненту ![]() (рис.4). Получим отсчеты прореженного
спектра (вторичной выборки) вида
(рис.4). Получим отсчеты прореженного
спектра (вторичной выборки) вида
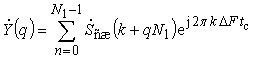 , (3)
, (3)
где ![]() – разрешающая способность по частоте
ДПФ из 128 отсчетов, определяемая как
– разрешающая способность по частоте
ДПФ из 128 отсчетов, определяемая как ![]() ;
;![]() – временное положение пика импульсной
характеристики, т. е. строба дальности (рис.2, кривая 5). Сама импульсная
характеристика q-го строба
дальности определяется как обратное ДПФ экспоненты
– временное положение пика импульсной
характеристики, т. е. строба дальности (рис.2, кривая 5). Сама импульсная
характеристика q-го строба
дальности определяется как обратное ДПФ экспоненты ![]()
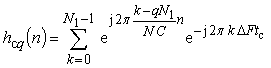 , (4)
, (4)
где n = 0..(N –1)∙C – индекс временных отсчетов; C –скважность при дополнении нулями
для построения значений импульсной характеристики внутри строба дальности. Каждый
q-й строб дальности имеет форму функции
sinN1x/sinx (рис.2, кривая 5), ширина которого определяется как ![]() . Отличаются стробы дальности лишь фазовым
множителем
. Отличаются стробы дальности лишь фазовым
множителем ![]() , величина фазового сдвига которого влияет
на обусловленность системы уравнений.
, величина фазового сдвига которого влияет
на обусловленность системы уравнений.
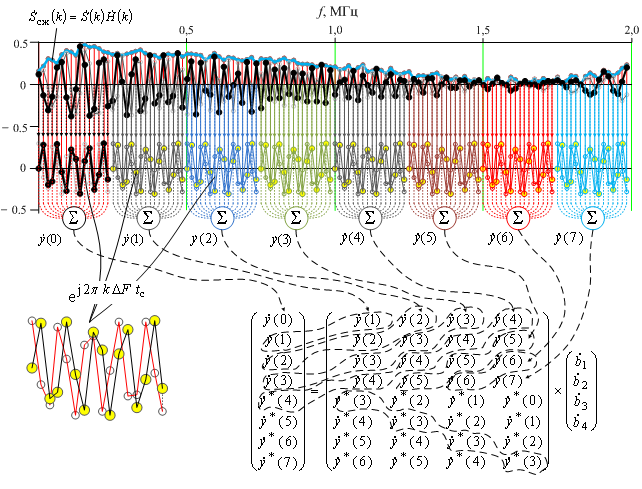
Рис. 4. Схема
формирования матрицы данных и системы уравнений когерентного
метода линейного
предсказания вперед-назад с прореживанием данных и порядком модели
P=4.
Эффективная длительность
импульсной характеристики строба дальности ![]() настолько
больше длительности сжатого импульса, насколько короче субвыборка частотного
спектра длиной N1 по сравнению с длиной всей частотной выборки
N. В рассматриваемом случае N1=16, а N=128, откуда следует, что длительность импульсной характеристики-строба
дальности в 8 раз больше ширины сжатого импульса.
настолько
больше длительности сжатого импульса, насколько короче субвыборка частотного
спектра длиной N1 по сравнению с длиной всей частотной выборки
N. В рассматриваемом случае N1=16, а N=128, откуда следует, что длительность импульсной характеристики-строба
дальности в 8 раз больше ширины сжатого импульса.
Для приведенного выше
примера зададим порядок модели линейного предсказания P=5. Имея Q = N/
N1 (в нашем случае Q = 8) отсчетов ![]() прореженного
спектра, сформируем блочную матрицу линейного предсказания вперед-назад
прореженного
спектра, сформируем блочную матрицу линейного предсказания вперед-назад ![]() вида
вида
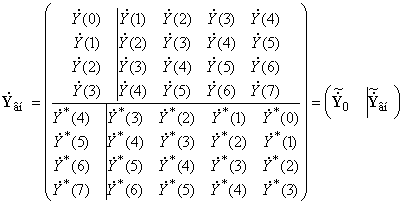 , (5)
, (5)
первые четыре строки которой
формируют ганкелеву матрицу, а вторые четыре строки – тёплицеву матрицу.
Составим из матрицы ![]() систему линейных уравнений
систему линейных уравнений
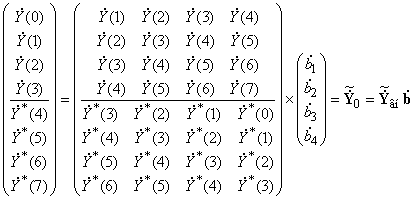 , (6)
, (6)
которую решая методом наименьших
квадратов, получим вектор весовых коэффициентов (ВВК) линейного предсказания
вперед-назад ![]() вида
вида
![]() , (7)
, (7)
![]() –
оператор эрмитового сопряжения. Несложно определить, что q-я импульсная характеристика (4),
представленная в виде
–
оператор эрмитового сопряжения. Несложно определить, что q-я импульсная характеристика (4),
представленная в виде
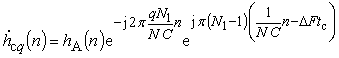 (8)
(8)
отличается от q+1-й фазовым множителем ![]() и имеет идентичную с остальными амплитудно-временную функцию
вида
и имеет идентичную с остальными амплитудно-временную функцию
вида
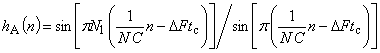 . (9)
. (9)
Оценка результирующей импульсной характеристики, определяемая как взвешенная сумма Q импульсных характеристик, имеет вид
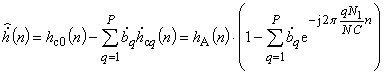 ,
,
откуда вычислим временную функцию линейного предсказания
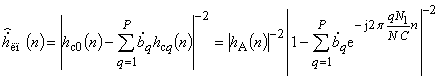 , (10)
, (10)
которая является разрешающей функцией.
Результаты моделирования
Моделировалась описанная выше ситуация отражения сигналов от трех точечных целей, находящихся на дальностях 12500 м, 12530 м и 12560 м и движущихся со скоростью 100 м/с в направлении радиолокатора. Девиация частоты 2 МГц с 0,5 мкс сжатого импульса обеспечивает величину релеевского элемента разрешения 75 м. На рисунке 5 показана временная функция одиночного сжатого ЛЧМ импульса (кривая 1) и результат обработки его спектра когерентным методом линейного предсказания вперед-назад с прореживанием (кривая 2). На временной функции линейного предсказания видны раздельные пики в окрестностях значений временных задержек, соответствующих истинному положению рассеивающих центров по дальности. Весовые коэффициенты использовались также для составления и нахождения корней характеристического полинома вида
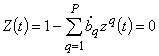 , (11)
, (11)
где ![]() –
аргумент полинома. После вычисления корней по их фазе, равной
–
аргумент полинома. После вычисления корней по их фазе, равной
![]()
вычисляются временные задержки
![]() .
.
При переходе от дискретных отсчетов к непрерывному времени, временная функция строба дальности будет иметь вид
![]() ,
,
где
![]() .
.
Вычисление амплитуд источников
выполнялось решением обратной задачи. Для оценок временных задержек ![]() определялась матрица
определялась матрица
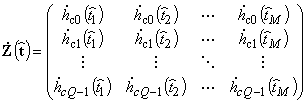 и
вектор
и
вектор
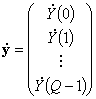 ,
,
связанные системой уравнений
![]() ,
,
откуда ![]() .
.
Вертикальные линии на рисунке 5 (линии 5) показывают значения амплитуд источников, соответствующие временным задержкам, определяемым через корни характеристического полинома.
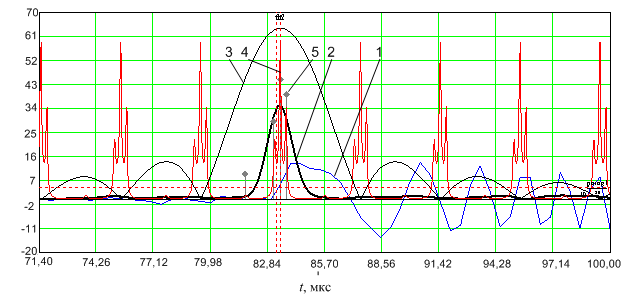
Рис. 5. Временные функции радиального профиля
сигнал, отраженный от трех точечных целей на дальностях 12500 м, 12530 м и 12560 м –1; модуль сжатого отраженного сигнала –2; временная функция строба дальности, определяемого фильтром предварительной обработки с прямоугольной АЧХ – 3; временная функция когерентного метода линейного предсказания вперед-назад с прореживанием –4; амплитуды, соответствующие корням характеристического полинома – 5.
Результаты моделирования показали, что три источника в пределах релеевского элемента, определяемого шириной сжатого ЛЧМ импульса, наблюдаются раздельно. При этом ОСШ первого источника с учетом накопления при обработке выборки составило 36 дБ, а ОСШ второго и третьего источников – 34 дБ и 32 дБ соответственно.
Статистический анализ разрешающей способности
Тем не менее, в задачах сверхразрешения важное значениие имеет статистический анализ процедуры оценивания для разных сигнальных ситуаций. Например, при фиксированных ОСШ следует исследовать вероятность обнаружения одной из трех, двух из трех и трех из трех источников, а также дисперсии измерения их временных задержек для разных расстояний центров отражения друг от друга. В классических задачах разрешающую способность по измеряемому параметру определяют как минимальную величину разности параметров двух источников. Однако в задаче сверхразрешения присутствие третьего, четвертого и более источников существенно влияет на обусловленность систем уравнений относительно ВВК. Поэтому для исследования разрешающей способности методов спектрального анализа имеет смысл рассматривать задачу разрешения двух источников в присутствии остальных.
Для наглядности представления результатов на график (рис. 6) выведены 10 из 200 временных функций радиального профиля, полученных для приведенной выше сигнальной ситуации при разных реализациях шума.
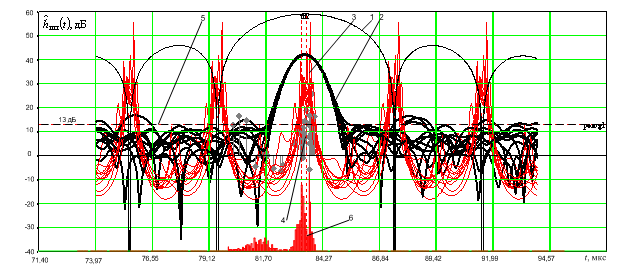
Рис. 6. Ансамбль из 10 реализаций временных функций радиального профиля
временная функция строба дальности, определяемого фильтром предварительной обработки с прямоугольной АЧХ – 1; модуль сжатого отраженного сигнала –2; временная функция когерентного метода линейного предсказания вперед-назад с прореживанием –3; амплитуды, соответствующие корням характеристического полинома – 4; линия порога 13 дБ – 5; гистограмма распределения значений корней характеристического полинома, с превышающими порог 13 дБ значениями амплитуды –6.
Вероятности одновременного обнаружения источников по превышению амплитуд корней порога в 13 дБ исследовались по 200 реализациям (рис. 6, гистограмма 6) одной и той же смеси сигналов при разных шумах. Исследование показало, что при ОСШ 36 дБ вероятности обнаружения первого, второго и третьего источников в отдельности составили P1=0,69, P2=0,96, P3=0,8. Вероятности совместного обнаружения первого второго, первого третьего и второго третьего источников составили P12=0,65, P13=0,49, P23=0,78 (рис.7). Вероятность одновременного обнаружения трех источников составила P123=0,47. Очевидно, что с увеличением ОСШ вероятности одновременного обнаружения нескольких источников будет возрастать.
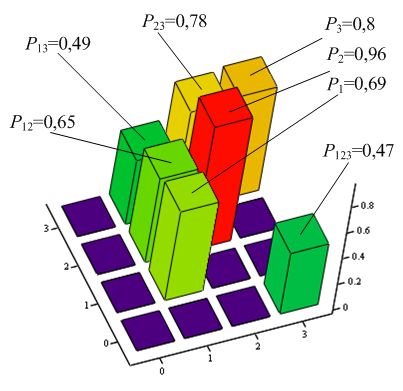
Рис. 7. Вероятности одновременного обнаружения нескольких источников при ОСШ 36 дБ.
По сравнению с рассмотренным методом линейного предсказания с когерентным накоплением и прореживанием исходный метод линейного предсказания с порядком модели 40, использующий 128 отсчетов выборки дает уверенное разрешение всего лишь двух источников на дальностях 12500м и 12560 м (рис.8). Из рисунка видно, что ни одна из реализаций не обеспечивает разрешения источника на дальности 12630 м, что свидетельствует о большей эффективности метода линейного предсказания с когерентным накоплением и прореживанием. Улучшение разрешающей способности когерентного метода по сравнению с исходным является лучшая обусловленность системы уравнений благодаря прореживанию данных и предварительной обработке с когерентным накоплением. использование временного строба (когерентного суммирования в частотной области) позволяет не терять энергию при прореживании данных, а само прореживание снижает линейную зависимость столбцов и строк матрицы данных, формирующей корреляционную матрицу сигналов. Это и позволяет снизить обусловленность системы уравнений линейного предсказания и повысить эффективность сверхразрешения источников.
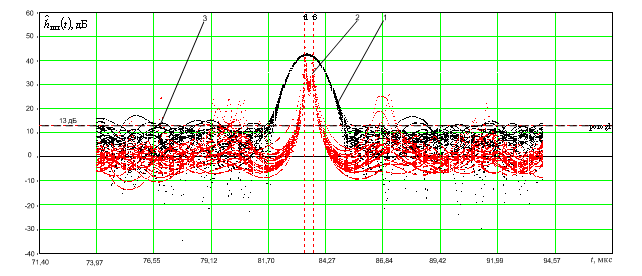
Рис. 8. Ансамбль из 200 реализаций временных функций радиального профиля исходного метода линейного предсказания вперед-назад
модуль сжатого отраженного сигнала –1; временная функция исходного метода линейного предсказания вперед-назад –2; порог 13 дБ – 3.
Заключение
Рассмотренный в статье когерентный подход применим к обработке любых импульсных сигналов, а также сигналов с перестройкой частоты. Основной особенностью является обработка данных в частотной области с их преобразованием во временную область аналогично подходам, при оценивании частотного или пространственного спектров, в которых осуществляется переход от времени к частоте или от пространственной выборки к пространственной частоте.
Метод, рассмотренный в статье, может применяться при обработке, как отсчетов частотного спектра, так и пространственных отсчетов или отсчетов времени.
Исследование показало, что из-за лучшей обусловленности КМ приведенный когерентный подход обеспечивает сверхразрешение при более низких ОСШ, чем исходный метод линейного предсказания, а также лучшую чувствительность к наличию или отсутствию источников в смеси сигнала и шума. При этом порядок модели существенно ниже, что приводит к большому выигрышу в вычислительных затратах. Оценка корреляционной матрицы может быть использована для получения спектральных функций методов MUSIC, EV, ESPRIT обеспечивающих сверхрелеевское разрешение.
В заключение авторы выражают благодарность профессору В.В.Абраменкову и Ю.И.Савинову за плодотворные дискуссии, позволившие лучше осмыслить вопросы данной тематики и более качественно подготовить материал.
Литература
1. Cook C. E., Bernfeld M. Radar Signals. An Introduction To Theory And Application. Academic Press New York, London, 1967
2. Теоретические основы радиолокации / Под ред. Ширмана Я. Д. Учебное пособие для вузов. М., Советское радио, 1970, 560 с.
3. Ширман Я. Д. Разрешение и сжатие сигналов. М., «Сов. Радио», 1974, 360 с.
4. Радиоэлектронные системы: основы построения и теория. Справочник. Изд. 2-е, перераб. и доп. / Под ред. Я. Д. Ширмана – М., Радиотехника, 2007, 512 с.
5. Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения / Пер. с англ. М.: Мир, 1990.
6. Stoica P, Moses R. L. Introduction to Spectral Analysis. New Jersey, Prentice-Hall, Inc. 1997, 319 p.
7. Лайонс Ричард. Цифровая обработка сигналов/ Пер. с англ. Под ред. А. А. Бритова. М., Бином, 2006, 654 с.