УДК 621.391
ГЕНЕРАТОР ФРАКТАЛЬНОГО ШУМА ПРОИЗВОЛЬНОЙ РАЗМЕРНОСТИ
С. А. Останин
Алтайский государственный университет, г. Барнаул
Получена 26 июня 2012 г., после доработки - 2 июля 2012 г.
Аннотация. Описан генератор электрического, акустического и оптического шума произвольной фрактальной размерности. Генератор может быть использован, в том числе, для целей математического моделирования. Приведены основные блок-схемы программ генератора, выполненных на LabVIEW, осциллограммы и спектрограммы сигналов генератора.
Ключевые слова: генератор шума, фракталы, дробные размерности, LabVIEW.
Abstract. We describe
a generator of
electric, acoustic and optical noise of arbitrary fractal dimension.
The
generator can be used, including for the purposes of mathematical
modeling. The
basic flow chart generator software implemented using LabVIEW, waveform and
spectrogram signal generator.
Keywords: noise generator, fractals, fractional dimension, LabVIEW.
Фрактальные свойства присущи характеристикам различных объектов и процессов, которые являются предметом исследования физики [1-6], геометрии и топологии [7], медицины и биологии [8], экономики [9]. В связи с этим представляет интерес создание приборов генерирующих физические сигналы различной природы со свойствами стохастических фракталов с целью изучения свойств фрактальных объектов и процессов. Генераторы фрактального шума используют, например, для математического моделирования фрактальных шероховатых поверхностей [10, 11], рассеивающих поверхностей [12], сетевого трафика в компьютерных сетях [13], фрактальных сигналов [14-17], описания кинетики фазовых превращений [18], моделирования экономических систем со свойствами самоподобия [19, 20]. Генераторы акустического фрактального шума используются, для проверки оценки акустических свойств помещений, концертных залов [21, 22], защиты речевой информации [23]. Генераторы фрактального шума напряжения применяются для проверки и настройки радиоэлектронных устройств, каналов связи, при поверке и калибровке средств измерений [24].
В основе работы аналоговых генераторов фрактального шума положен принцип прямого усиления шумового сигнала источника шума (полупроводниковых диодных генераторов шума). Для получения «розового» шума используют резистивно-емкостные фильтры со спадающим спектром [24]. Другие аналоговые генераторы используют источники шума со спадающей спектральной характеристикой. К недостатку аналоговых способов генерации фрактального шума относится зависимость свойств генерируемого сигнала от набора используемых компонентов, вследствие чего отсутствует возможность выбора произвольного значения фрактальной размерности шума. Известны также цифровые генераторы шума, работа которых основана на формировании бинарных псевдослучайных последовательностей с дальнейшей аналоговой или цифровой фильтрацией для получения необходимых статистических свойств выходного сигнала (СССР, а.с. 1665492). Цифровые способ генерации отличается высокой стабильностью работы и высокой степенью стохастичности в пределах большого периода времени, однако и для них существует проблема произвольного выбора фрактальной размерности. Для создания математической модели фрактального шума используют, например, функцию Вейерштрасса [15]. Фрактальная размерность генерируемого массива числовых значений является параметром этой функции и может принимать произвольные значения на ограниченном интервале. Особенностью такого генератора является не случайный характер шума, что ограничивает его сферу применения в области моделирования природных явлений.
Предлагаемый простой генератор фрактального шума отличается тем, что генерирует стохастический шум произвольной размерности и может быть использован в целях математического моделирования и физического эксперимента.
Математической основой созданного нами генератора шума является Фурье-преобразование белого шума с нормальным распределением с последующей модификацией спектра и выполнением обратного Фурье-преобразования.
Известно, что
Фурье-преобразование
сигнала ![]() имеет
вид:
имеет
вид:
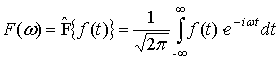 ,
(1)
,
(1)
здесь ![]() –
оператор
Фурье-преобразования. В пространстве частот дифференцированию функции
–
оператор
Фурье-преобразования. В пространстве частот дифференцированию функции ![]() соответствует
произведение вида
соответствует
произведение вида
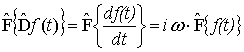 ,
(2)
,
(2)
где ![]() –
оператор
однократного дифференцирования.
–
оператор
однократного дифференцирования.
Производную по времени
функции ![]() можно
получить следующим образом:
можно
получить следующим образом:
![]() .
(3)
.
(3)
Для производной
произвольного порядка ![]() , в том
числе не целого, вводится
обобщение [25]:
, в том
числе не целого, вводится
обобщение [25]:
![]() .
(4)
.
(4)
Для интеграла
произвольного порядка ![]() справедливо
справедливо
![]() ,
(5)
,
(5)
где ![]() – оператор
интегрирования порядка
– оператор
интегрирования порядка ![]() .
.
Правые части выражений (4)
и (5)
отличаются только знаком перед ![]() , следовательно,
построив прибор осуществляющий преобразование вида (4), можно выполнять
интегро-дифференцирование произвольного, в том числе дробного, порядка.
В
результате дробного интегрирования нормального шума мы получим
стохастический
фрактал. В работе [26] показано, что при
, следовательно,
построив прибор осуществляющий преобразование вида (4), можно выполнять
интегро-дифференцирование произвольного, в том числе дробного, порядка.
В
результате дробного интегрирования нормального шума мы получим
стохастический
фрактал. В работе [26] показано, что при ![]() ,
для интеграла вида (5), показатель Херста Н линейно
связан с
,
для интеграла вида (5), показатель Херста Н линейно
связан с ![]() как
как
![]() ,
следовательно,
фрактальная размерность
,
следовательно,
фрактальная размерность ![]() фрактального
шума
определяется как
фрактального
шума
определяется как
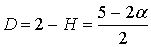 .
(6)
.
(6)
Заметим, что выражения (4) и (5) представляют
собой фильтр с
передаточной характеристикой, определяемой константой ![]() .
Фильтр такого типа
.
Фильтр такого типа ![]() имеется
в составе виртуальных
приборов среды визуального программирования LabVIEW. С учетом ранее введенных
обозначений
имеется
в составе виртуальных
приборов среды визуального программирования LabVIEW. С учетом ранее введенных
обозначений
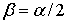 ,
, 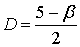 .
(7)
.
(7)
На рисунке 1 представлена блок-диаграмма генератора шума произвольной фрактальной размерности, построенная с использованием такого инверсного фильтра.
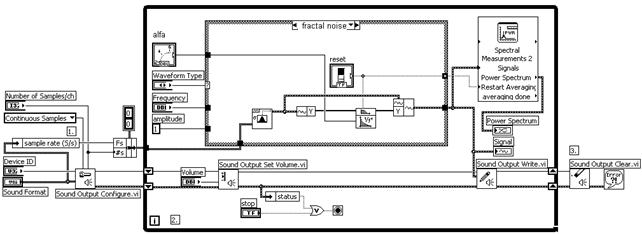
Рис. 1. Блок-диаграмма генератора шума произвольной фрактальной размерности.
В качестве источника
исходного сигнала использовался генератор белого шума с нормальным
распределением, имеющийся в наборе виртуальных приборов LabVIEW. Белый шум проходит через
инверсный
фильтр с показателем ![]() ,
значение которого
можно устанавливать средствами контроля лицевой панели прибора.
Цифровой сигнал
поступает на вход аналого-цифрового преобразователя звуковой карты
компьютера
или подключаемого аналого-цифрового преобразователя. К линейному выходу
звуковой
карты подключен усилитель, нагрузкой которого является динамическая
головка. Ширина
полосы спектра определяется максимальной частотой преобразования
код-напряжение
аналого-цифрового преобразователя. Кроме динамической головки нагрузкой
служили
диоды, излучающие в видимом и инфракрасном диапазоне (ток покоя
диодов
задавался внешним источником). Таким образом, описанное
устройство
представляет собой генератор электрического, акустического и
оптического шума
произвольной фрактальной размерности. На рисунках 2-5 показаны
осциллограммы
сигналов генератора при некоторых часто используемых
значениях показателя
,
значение которого
можно устанавливать средствами контроля лицевой панели прибора.
Цифровой сигнал
поступает на вход аналого-цифрового преобразователя звуковой карты
компьютера
или подключаемого аналого-цифрового преобразователя. К линейному выходу
звуковой
карты подключен усилитель, нагрузкой которого является динамическая
головка. Ширина
полосы спектра определяется максимальной частотой преобразования
код-напряжение
аналого-цифрового преобразователя. Кроме динамической головки нагрузкой
служили
диоды, излучающие в видимом и инфракрасном диапазоне (ток покоя
диодов
задавался внешним источником). Таким образом, описанное
устройство
представляет собой генератор электрического, акустического и
оптического шума
произвольной фрактальной размерности. На рисунках 2-5 показаны
осциллограммы
сигналов генератора при некоторых часто используемых
значениях показателя ![]() . Как
видно из рисунков, с ростом
. Как
видно из рисунков, с ростом ![]() сигнал
становится более «гладким»,
доля высокочастотных составляющих в шуме уменьшается. При
сигнал
становится более «гладким»,
доля высокочастотных составляющих в шуме уменьшается. При ![]() (рисунок
2) генерируется белый шум,
эквивалентный исходному. При
(рисунок
2) генерируется белый шум,
эквивалентный исходному. При ![]() (рисунок
3) генерируется
шум с размерностью
(рисунок
3) генерируется
шум с размерностью ![]() . Шум
такого вида характерен,
например, для некоторых радиотехнических цепей и элементов, профиля
шероховатых
поверхностей. На рисунке 4 показан сигнал генератора при
. Шум
такого вида характерен,
например, для некоторых радиотехнических цепей и элементов, профиля
шероховатых
поверхностей. На рисунке 4 показан сигнал генератора при ![]() ,
которому соответствует броуновский
процесс с дробной размерностью
,
которому соответствует броуновский
процесс с дробной размерностью ![]() . Сигналы
такого вида можно
использовать, например, для моделирования временных рядов финансовых
рынков
[27]. При увеличении показателя
. Сигналы
такого вида можно
использовать, например, для моделирования временных рядов финансовых
рынков
[27]. При увеличении показателя ![]() до
3 шум
становиться одномерным (
до
3 шум
становиться одномерным (![]() ). Таким
шумом
моделируют процесс «инфракрасной катастрофы» (процессы с неограниченной
дисперсией) [28, 29].
). Таким
шумом
моделируют процесс «инфракрасной катастрофы» (процессы с неограниченной
дисперсией) [28, 29].
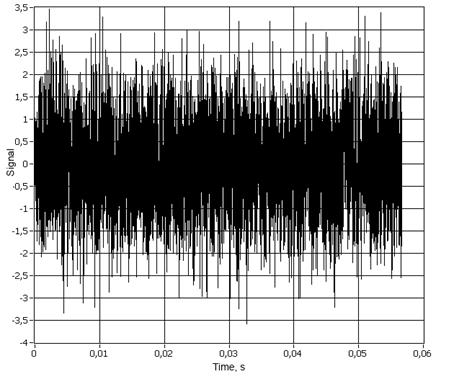
Рис.
2. Сигнал генератора при ![]() .
.
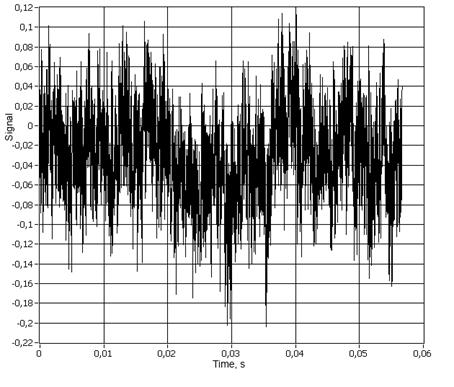
Рис.
3. Сигнал генератора при ![]() .
.
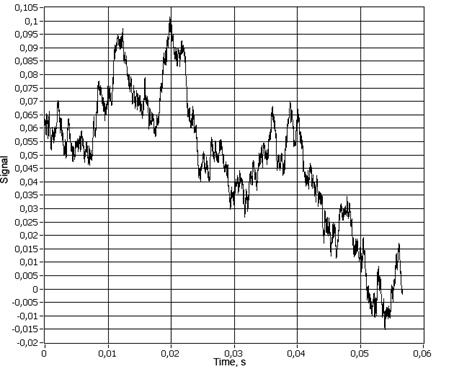
Рис.
4. Сигнал генератора при ![]() .
.
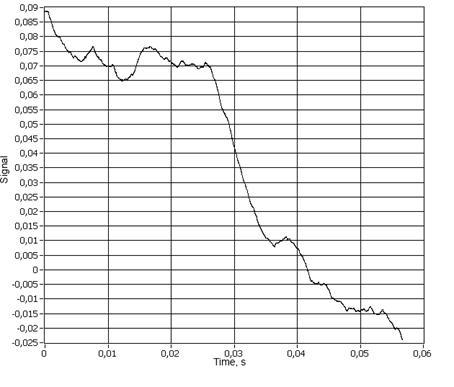
Рис.
5. Сигнал генератора при ![]() .
.
Размерность ![]() сигналов
генератора шума (рисунки 2-5) была
оценена по их спектрам мощности (рисунки 6-9), построенным в двойном
логарифмическом масштабе. С ростом
сигналов
генератора шума (рисунки 2-5) была
оценена по их спектрам мощности (рисунки 6-9), построенным в двойном
логарифмическом масштабе. С ростом ![]() изменяется
отношение приращения логарифма спектральной мощности к приращению
логарифма
частоты. По значениям спектров методом наименьших квадратов строились
прямые
линии, наклон которых давал оценку показателя
изменяется
отношение приращения логарифма спектральной мощности к приращению
логарифма
частоты. По значениям спектров методом наименьших квадратов строились
прямые
линии, наклон которых давал оценку показателя ![]() и
размерности
и
размерности ![]() .
Относительное отклонение оценок
размерности шума
.
Относительное отклонение оценок
размерности шума ![]() от
заданных в программе
генератора составило 0,5%. Кроме того, по нелинейности спектра
мощности в
двойном логарифмическом масштабе можно оценить качество (фрактальность)
шума
генератора. Как видно из рисунков 6-9, линейная зависимость наблюдается
в
широком диапазоне частот (от 50Гц до 20кГц) при различных значениях
от
заданных в программе
генератора составило 0,5%. Кроме того, по нелинейности спектра
мощности в
двойном логарифмическом масштабе можно оценить качество (фрактальность)
шума
генератора. Как видно из рисунков 6-9, линейная зависимость наблюдается
в
широком диапазоне частот (от 50Гц до 20кГц) при различных значениях ![]() (от
0 до 3) и
(от
0 до 3) и ![]() (от
1 до 2). Нелинейность логарифмического спектра мощности в области от
20кГц до
верхней границы 88.2кГц обусловлена близостью к частоте выборки и
преобразования сигнала (88.2кГц).
(от
1 до 2). Нелинейность логарифмического спектра мощности в области от
20кГц до
верхней границы 88.2кГц обусловлена близостью к частоте выборки и
преобразования сигнала (88.2кГц).
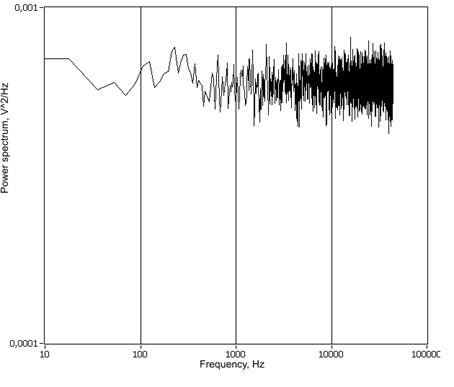
Рис.
6. Спектр мощности сигнала
генератора шума при ![]() .
.
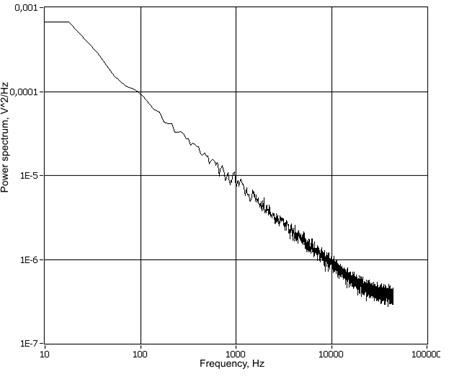
Рис.
7. Спектр мощности сигнала
генератора шума при ![]() .
.
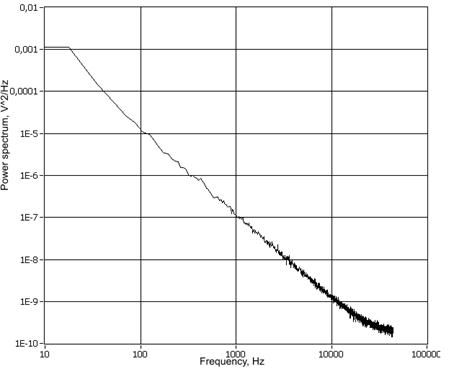
Рис.
8. Спектр мощности сигнала
генератора шума при ![]() .
.
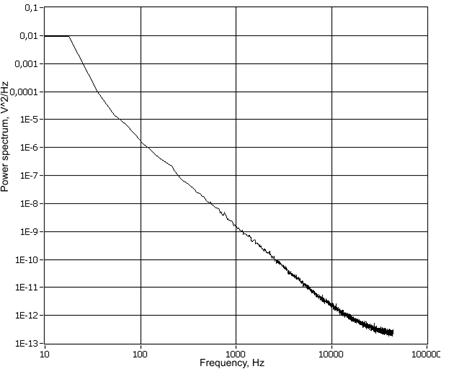
Рис.
9. Спектр мощности сигнала
генератора шума при ![]() .
.
С целью дополнительной верификации генератора шума был создан прибор интегро-дифференцирования дробного порядка, блок-диаграмма которого показана на рисунке 10. В качестве тестовой функции использовался моноимпульс Гаусса вида
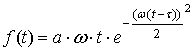 ,
(8)
,
(8)
где а –
параметр определяющий
амплитуду импульса, ![]() – задержка
импульса. Этот тип
функции выбран для простоты анализа полученных результатов (вид
производной и
интеграла первого порядка моноимпульса Гаусса хорошо известен).
Сравнивая
интеграл моноимпульса Гаусса, полученный аналитически, с
генерируемым
интегралом, можно оценить погрешность генератора шума. Прибор
представляет
собой модификацию генератора шума (рисунок 1): генератор белого шума
заменен на
генератор моноимпульса Гаусса. Для интегро-дифференцирования
дробного порядка
функций любого вида достаточно установить блок чтения данных из файла
(он
имеется в стандартном наборе виртуальных приборов LabVIEW) вместо генератора
моноимпульса Гаусса. Файл должен
содержать одномерный массив описывающий функцию. Формат представления
данных –
один текстовый столбец, по одному значению функции в строке. На рисунке
11
показан исходный моноимпульса Гаусса (
– задержка
импульса. Этот тип
функции выбран для простоты анализа полученных результатов (вид
производной и
интеграла первого порядка моноимпульса Гаусса хорошо известен).
Сравнивая
интеграл моноимпульса Гаусса, полученный аналитически, с
генерируемым
интегралом, можно оценить погрешность генератора шума. Прибор
представляет
собой модификацию генератора шума (рисунок 1): генератор белого шума
заменен на
генератор моноимпульса Гаусса. Для интегро-дифференцирования
дробного порядка
функций любого вида достаточно установить блок чтения данных из файла
(он
имеется в стандартном наборе виртуальных приборов LabVIEW) вместо генератора
моноимпульса Гаусса. Файл должен
содержать одномерный массив описывающий функцию. Формат представления
данных –
один текстовый столбец, по одному значению функции в строке. На рисунке
11
показан исходный моноимпульса Гаусса (![]() ,
интеграл нулевого порядка).
,
интеграл нулевого порядка).
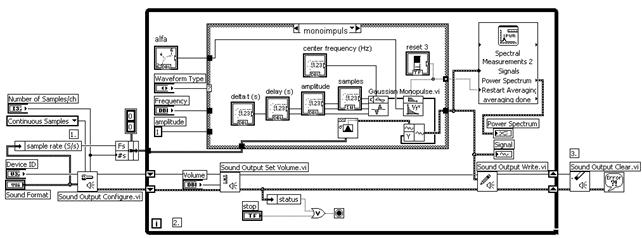
Рис. 10. Блок-диаграмма прибора дробного интегро-дифференцирования.
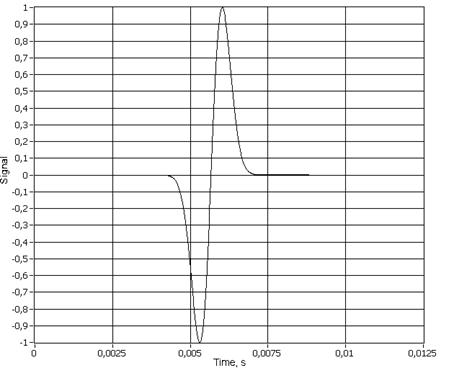
Рис.
11. Моноимпульс Гаусса (![]() ).
).
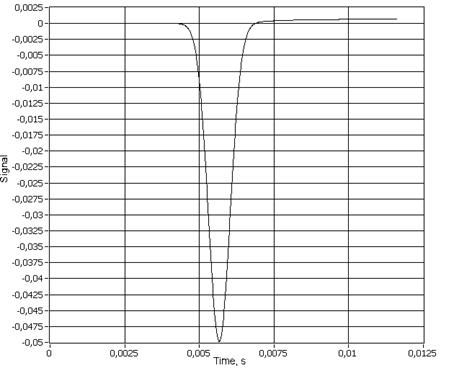
Рис.
12. Интеграл моноимпульса Гаусса
первого порядка (![]() ).
).
Интеграл первого порядка
моноимпульса
Гаусса (рисунок 12) представляет собой функцию Гаусса. Статистический
анализ
показал, что операция интегрирования первого порядка выполняется с
относительной погрешностью около 1%. Полученные удовлетворительные
оценки
погрешностей интегралов 1% и относительного отклонения оценок
размерности шума ![]() 0,5%
позволяют сделать заключение о возможности
использования описанного генератора для создания физических
стохастических
фрактальных сигналов [30] и математического моделирования
фрактального шума.
0,5%
позволяют сделать заключение о возможности
использования описанного генератора для создания физических
стохастических
фрактальных сигналов [30] и математического моделирования
фрактального шума.
Литература
1. Мандельброт Б. Фрактальная геометрия природы. – М.: «Институт компьютерных исследований», 2002.
2. Федер Е. Фракталы. – М: «Мир», 1991.
3. Фракталы в физике. Труды 6-го международного симпозиума по фракталам в физике, 1985. – М.: «Мир», 1988.
4. Локшин А.А., Суворова Ю.В. Математическая теория распространения волн в средах с памятью – М.: МГУ, 1982.
. Волынцев А. Б. Наследственная механика дислокационных ансамблей. Компьютерные модели и эксперимент – Иркутск: Изд-во Иркутского ун-та, 1990.
6. Работнов Ю.Н. Элементы наследственной механики твердых тел – М.: Наука, 1977.
7. Фоменко А.Т. Наглядная геометрия и топология. – М.: изд-во МГУ, 1993.
8. Лебедева Н.Н., Бецкий О.В. Фракталы в биологии и медицине // Биомедицинские технологии и радиоэлектроника, №10, 2002. с.49-59.
9. Мандельброт Б., Ричард Л. Хадсон Непослушные рынки: фрактальная революция в финансах. – М.: «Вильямс», 2006.
10. В.И. Курдюков, А.К. Остапчук, В.Е. Овсянников, Е.Ю. Рогов Разработка фрактальной математической модели шероховатости поверхности // Вестник КузГУ. – Кемерово: Изд-во кузбасского государственного технического университета. – 2008. - №5. – с. 43-46.
11. Горохов Д.Б., Огар П.М. Моделирование фрактальных шероховатых поверхностей // Математическое моделирование, численные методы и комплексы программ: СПбГАСУ. СПб, - 2004. - Вып. 10 - С. 235-240.
12. Лактюнькин А.В. Моделирование фрактальных недифференцируемых поверхностей и процессов рассеяния ими электромагнитных волн // Нелинейный мир. 2007. Т. 5. № 5. С. 286 -287.
13. Фрактальный анализ и процессы в компьютерных сетях : учеб. пособие / Ю.Ю. Громов, Н.А. Земской, О.Г. Иванова, А.В. Лагутин, В.М. Тютюнник. – 2-е изд., стереотип. – Тамбов : Изд-во Тамб. гос. техн. ун-та, 2007.
14. Капранов М.В., Хандурин А.В. Сигналы с аддитивной фрактальной структурой для передачи информации. // Электромагнитные волны и электронные системы. №2, Т.16., 2011. с.23-36.
15. Короленко П.В., Маганова М.С., Меснянкин А.В. Новационные методы анализа стохастических процессов и структур в оптике. Фрактальные и мультифрактальные методы, вейвлет-преобразования. Учебное пособие. – М.: Изд-во Моск. ун-та, Научно-исследовательский институт ядерной физики им. Д.В. Скобельцына, 2004.
16. Потапов А.А. Фракталы в радиофизике и радиолокации. – М.: Логос, 2002
17. Потапов А.А. Фракталы в радиофизике и радиолокации: Топология выборки – 2-е изд., перераб. и доп. – М.: Университетская книга, 2005.
18. Д.В. Пелегов, Использование фрактального формализма для описания кинетики фазовых превращений в конечных системах. Диссертация на соискание ученой степени кандидата физико-математических наук /: Урал. Гос. Ун-т. Екатеринбург, 2000.
19. Ширяев А.Н. Основы стохастической финансовой математики – М.: «Фазис», 1998.
20. Соловьёв В.И. Стохастические модели математической экономики и финансовой математики: Учебное пособие. – М.: ГУУ, 2001.
21. Мунин А.Г., Диева Е.А. Акустика Рахманиновского зала // Промышленное и гражданское строительство, №1, 2007.
22. Ковригин С.Д. Архитектурно-строительная акустика: Учеб. пособие для вузов. – М.: Высш. школа, 1980.
23. Хорев А.А. и Макаров Ю.К. К оценке эффективности защиты акустической (речевой) информации // Специальная Техника, №5, 2000.
24. Справочник по радиоизмерительным приборам: В 3-х т.; Под ред. В. С. Насонова – М.: Сов. радио, 1979.
25. Kilbas A.A., Srivastava H.M., Trujillo J.J. Theory and Application of Fractional Differential Equations. – Amsterdam, Elsevier, 2006.
26.
Flandrin
P. On the Spectrum of Fractional Brownian Motions //
IEEE Trans. on Info. Theory, 1989, Vol. IT-35, No.1, p.197-199.
27. Петерс Э. Фрактальный анализ финансовых рынков: применение теории хаоса в инвестициях и экономике – М.: Интернет-трейдинг, 2004.
28. Mandelbrot B. B. Weierstrass Functions and Kin. Ultraviolet and Infrared Catastrophe. – The Fractal Geometry of Nature. New York: W. H. Freeman, 1983.
29. Mandelbrot B. B. Gaussian Self-affinity and Fractals: Globality, the Earth, 1/f Noise and R/S. – Springer, 2002.
30. Останин С.А. Оценка параметров фракталов в смеси хаотических сигналов по спектру мощности // Журнал радиоэлектроники [электронный журнал]. – 2012 г. - №5 - Режим доступа: http://jre.cplire.ru/jre/may12/3/text.html