УДК: 004.8, 004.94, 51-74, 621.37

ПОСТРОЕНИЕ НЕЙРОННЫХ СЕТЕЙ ПРЯМОГО РАСПРОСТРАНЕНИЯ С ИСПОЛЬЗОВАНИЕМ АДАПТИВНЫХ ЭЛЕМЕНТОВ

Е. Н. Ефимов, Т. Я. Шевгунов

Московский авиационный институт

(национальный исследовательский университет)

 

Получена 13 августа 2012 г.
 

Аннотация. В данной работе рассматриваются сети прямого распространения сигнала, обучение которых проводится с использованием методов, основанных на процессе обратного распространения ошибки. Нейронная сеть описывается в виде системы связанных двунаправленными сигнальными связями адаптивных элементов, обеспечивающих преобразования сигналов при прямом и обратном распространении. Ключевым преимуществом такого подхода является то, что элементы, входящие в состав сети, могут представлять собой не только классические нейроны или их слои, но могут быть сложными подсистемами, реализующими требуемые передаточные функции. Разработанная методика построения нейронной сети реализована в виде прототипа программного обеспечения, включающего библиотеку классов адаптивных элементов. В работе приведены результаты численного моделирования для решения задачи аппроксимации сверхкороткоимпульсного радиолокационного сигнала и классификации случайного процесса.

Ключевые слова: нейронная сеть; обратное распространение ошибки; адаптивный элемент; сигналы и системы; метод градиентного спуска; SageMath; Python.

Abstract. This article deals with feedforward artificial neural networks learned by supervised methods based on the error backpropagation. The artificial neural networks of mentioned type can be defined as the systems of interconnected adaptive elements transforming signals in two concurrent directions: either backward or forward. The key advantage of approach proposed is that the single adaptive element is no longer necessary to be a classical neuron or a layer of neurons, but it can be an arbitrary subsystem with any desirable transfer function. The presented method of neural network design is implemented in the developed software prototype along with the library of common adaptive elements. This paper also demonstrates the comparison of the results obtained by numerical simulation of the ultra-short-pulse radar response and by the classification of two random processes.

Keywords: neural network, backpropagation, adaptive element, signals and systems, gradient descent, Sage Math, Python.

Введение

Традиционная нейронная сеть прямого распространения представляет собой систему взаимодействующих адаптивных элементов – нейронов [1, 2], каждый из которых выполняет определенное функциональное преобразование над сигналами. Существуют два основных методологических подхода к описанию процессов нейросетевой обработки сигналов: математический, основанный на описании сети в терминах функциональных преобразований, и системный, представляющий сеть в форме взаимодействующих подсистем, в которых происходит преобразование входных сигналов и сигналов. В настоящем исследовании используется системный подход, на основе которого предложена методика, предполагающая разбиение всей нейронной сети на блоки простых адаптивных элементов.

Так в работе [3] было впервые предложено представить процесс обратного распространения ошибки с помощью функциональной схемы, которая получила название системной диаграммы представления обратного распространения (backpropagation diagrammatic representation). Такая диаграмма является наглядным средством, позволяющим описать функционирования алгоритма обратного распространения. Однако в своей работе авторы используют её как вспомогательный инструмент для упрощения вывода необходимых выражений при анализе динамических нейронных сетей, предназначенных для обработки сигналов, являющихся функциями времени. Этот инструмент также был заимствован впоследствии другими авторами, например [2, 4], как наглядный способ представления правил обратного распространения при изучении предмета нейронных сетей.

В настоящей работе сделана попытка развить и систематизировать предложенный способ описания. Для этого авторы предлагают построить нейронную сеть на основе адаптивных элементов, которые предполагается сохранять отдельными друг от друга при построении математической модели сети. Между элементами организуются двунаправленными связи, которые в целом образуют два совмещенных графа для описания прямого и обратного распространения сигнала. Каждый элемент осуществляет обработку сигналов в прямом и обратном направлении, а также выполняет подстройку своих адаптируемых параметров в фазе обучения сети с использованием одного из известных методов обучения [5].

В общем виде некоторый адаптивный элемент осуществляет преобразование T входного вектора x в выходной вектор y:

                                                                                                        (1)

где под вектором θ подразумевается вектор параметров этого преобразования. Каждый адаптивный элемент обладает некоторым вектором параметров, значение которого определяется в процессе обучения. Адаптивные элементы связаны в структуре сети между собой при помощи двунаправленных каналов, обеспечивающих прохождение сигналов в прямом и обратном направлениях, что схематично показано на рис. 1.

 

 

Рис. 1. Структура сигнальных связей адаптивного элемента.

 

Предполагается, что для нейронной сети существует два основных рабочих режима: режим эксплуатация и режим обучения. В режиме эксплуатации используется прямое прохождение, которое позволяет при известной форме преобразования T и векторе параметров θ получить отклик y_F элемента на некоторый входной сигнал x_F. В режиме обучения выполнятся корректировка вектора параметров на основе сигнала ошибки x_B.

Обучение нейронной сети

В данной работе рассмотрено обучение с учителем (supervised learning), при котором обучаемой сети последовательно представляется набор примеров из обучающего множества. Примеры представляют собой пары эталонных входных воздействий и желаемых выходных сигналов. Процесс обучения проходит циклически, на каждой итерации выполняется расчет сигналов при прямом и обратном распространениях, после чего сигналы ошибок используются для формирования локальных градиентов векторов адаптируемых параметров. Вычисленные локальные градиенты используются для последующей корректировки адаптируемых параметров [2, 6]. Используемые режимы обучения – это последовательный режим (online), при котором подстройка параметров происходит после каждого примера, и пакетный (batch), при котором подстройка осуществляется на основе кумулятивного локального градиента – суммы локальных градиентов по всем итерациям примеров из обучающего множества. В обоих режимах полный цикл представления множества шаблонов обучения, завершающийся подстройкой параметров, называется эпохой обучения сети. Для количественной оценки качества работы сети вводится функция потерь, имеющая смысл среднеквадратической ошибки (СКО):

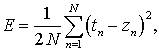                                                                                          (2)

где N – количество представленных шаблонов; t_n – желаемый, или целевой (target), выходной сигнал сети в n-ом шаблоне; z_n –выходной сигнал, вычисляемый сетью при подаче входного сигнала из n-ого шаблона.

На данном этапе исследования авторами рассматриваются только автономные методы обучения, которые для подстройки вектора параметров адаптивного элемента используют только те сигналы, которые присутствуют в самом рассматриваемом элементе. Корректирующее изменение Δθ_т для m-го элемента θ_т из вектора адаптируемых параметров θ вычисляется, на основе информации, полученной только из его локального градиента δθ_m и истории изменения этого локального градиента с течением эпох.

Метод градиентного спуска является самым простым методом обучения сети. Адаптируемый параметров  корректируется на величину  согласно выражению:

                                                                                                    (3)

где  – скорректированное значение параметра,  – исходное значение параметра,  – корректирующее изменение. При этом величина корректирующего изменения определяется выражением:

                                                                                                     (4)

где  – коэффициент скорости обучения,  – локальный градиент элемента.

В выражении (4) знак минус перед коэффициентом необходим для изменения параметра  как аргумента функции  в сторону уменьшения значения последней. Важно уделять особое внимание выбору коэффициента скорости обучения : маленькая величина коэффициента приведёт к увеличению времени (количества итераций), необходимого для обучения, однако слишком большая величина приведёт к дестабилизации обучения ввиду чрезмерного приращения параметра так, что он будет «проскакивать» оптимальное значение. О влиянии коэффициента обучения будет сказано позднее в результатах численного моделирования. Как привило, значение коэффициента  принимают из условия:

                                                                                                             (5)

Метод градиентного спуска является базовым методом, на основе которого строятся другие автономные методы первого и так называемого квазивторого порядка.

Одним из очевидных усовершенствований метода градиентного спуска является добавление эффекта инерции (momentum) при изменении параметров является методикой усреднения, позволяющей в ряде случаем значительно повысить стабильность процесса обучения (достижения параметрами своих оптимальных значений ). Данный метод, в целом, использует усреднённое значение изменений параметров в предыдущих эпохах для вычисления измерения параметра в текущей эпохе, что позволяет сделать изменение параметров более плавным. Используется экспоненциальное среднее значений измерений параметров за все предыдущие эпохи, в этом случае выражение для вычисления коррекции (4) принимает вид :

                                                                                (6)

где  – корректирующее изменение текущей (-ой) эпохи,  корректирующее изменение предыдущей эпохи,  – коэффициент инерции,  – коэффициент скорости обучения,  – локальный градиент элемента.

Коэффициент инерции  определяет меру влияния предыдущих подстроек на текущую и, как правило, выбирается исходя из условия:  

                                                                                                       

Левая часть в выражении (6) представляет собой влияние предыдущих подстроек значения параметра  на текущую подстройку, при этом корректирующее изменение предыдущей эпохи  взвешено коэффициентом инерции , следовательно, чем больше коэффициент инерции, тем более сильное влияние оказывает история изменения параметра на текущее изменение. Правая часть выражения повторяет соответствующее выражение (4) для метода градиентного спуска, однако включает взвешивающий коэффициент  для учёта доли влияния предыдущих эпох. В случае, когда коэффициент инерции  равен 0, метод Momentum вырождается в метод градиентного спуска, при этом история измерения корректирующих значений за предыдущие эпохи не влияет на корректирующее значение текущей эпохи (выражение (6) формально переходит в (4)).

В работе [3] подробно рассмотрен метод, известный под названием Delta-Bar-Delta. В отличие от метода градиентного спуска и момента, принципиальное расширение данного метода заключается в том, что для каждого адаптивного параметра вводится индивидуальный коэффициент скорости обучения. После каждой эпохи обучения происходит как подстройка адаптируемых параметров, так и подстройка коэффициента скорости обучения. Для упрощения выкладок рассмотрим один из адаптируемых параметров, который обозначим через . Для корректировки его скорости изменения вводится вспомогательный параметр (который мы обозначим через f) также изменяющийся с течением номера эпохи по правилу (7).

                                                                                          (7)

где коэффициент  () определяет «глубину памяти» накопления истории предыдущих значений градиента. Для текущей эпохи вспомогательный параметр  определяет градиент, накопленный за предыдущие эпохи. Если знак величины градиента текущей эпохи  совпадает со знаком коэффициента , то скорость обучения увеличивается, иначе – уменьшается. Величины изменений скорости обучения определяются выражением:

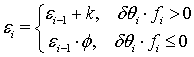                                                                          (8)

 

Параметры  и , выбираемые в диапазоне от нуля до единицы, определяют, насколько велико будет изменение скорости обучения при каждой подстройке. Вектор, составленный из значений скоростей , вычисляемых по формуле (8), и значение градиента  используются в формуле (4) для вычисления нового значения вектора адаптируемых параметров.

Адаптивные элементы

Использование автономных методов обучения позволяет построить сравнительно простые модели элементов, простейшие из которых показаны на рис. 2 а) – г).

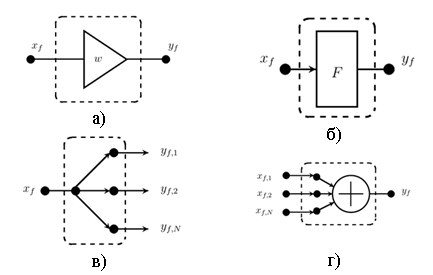
Рис. 2. Простейшие элементы нейронной сети:
а) адаптивный умножитель, б) безынерционный функциональный преобразователь, в)  разветвитель, г) сумматор.

 

Среди адаптивных элементов усилитель занимает центральное место, т.к. именно в нем реализуется подстройка коэффициентов сети в соответствие с выбранным методом обучения. Схематически усилитель представлен на рис. 2 а), он имеет один вход и один выход, при этом выходной сигнал определяется выражением:

                                                        .                                                   (9)

При обратном распространении сигнала усилитель не изменяет своего поведения, т.е. выходной сигнал является в  раз усиленным входным сигналом:

                                                                                                  (10)

Усилитель в процессе обучения нейронной сети способен изменять собственный коэффициент усиления, реализуя при этом адаптивные свойства сети.

Функциональный преобразователь является в общем виде элементом с одним входом, одним выходом и известной передаточной функцией . Поведение всех функциональных преобразователей при прямом и обратном прохождении сигналов определяются их функциями  и первыми производными .

Функциональный преобразователь показан на рис. 2 б), его выходной сигнал при прямом распространении определяется выражением 11.

                                                                                                      (11)

где  – входной сигнал при прямом распространении,  – выходной сигнал при прямом распространении,  – функция преобразования. При обратном распространении функциональный преобразователь представляет собой усилитель, при этом выходной сигнал определяется выражением:

                                                                                                          (12)

где  - входной сигнал при обратном распространении,  - выходной сигнал при обратном распространении,  - коэффициент усиления:

                                                                                                        (13)

Коэффициент усиления определяется выражением (13), что показывает зависимость поведения элемента при обратном распространении от значения первой производной функции f в точке x_f

Функциональные преобразователи входят в состав нейронов, формируя различные виды последних, при этом функция преобразования является функцией активации нейрона.

Для представленных элементов были получены функции преобразования сигналов при прямом прохождении сигнала и обратном распространении ошибки. Композиция простейших элементов позволяет построить классические структурные элементы сети прямого распространения – нейрон и нейронный слой, которые в свою очередь также могут быть описаны с использованием нотации адаптивных элементов.

 

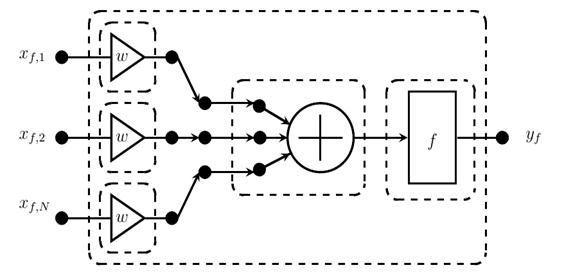
Рис. 3. Декомпозиция нейрона при прямом прохождении сигнала.

«Классический» нейрон модели МакКаллока-Питтса в парадигме построения нейронной сети на основе простых адаптивных элементов может быть реализован алгоритмически, либо композицией простейших элементов (сумматоров, усилителей и функциональных преобразователей). Алгоритмическая реализация, несомненно, обладает лучшей производительностью, однако для большей наглядности будет рассмотрена композиционная модель, она показана на рис. 3. Входные усилители индивидуальны для каждого входного сигнала, таким образом их коэффициенты, фактически, являются синоптическими весами  нейрона. Функциональный преобразователь на выходе в качестве функции преобразования содержит функцию активации нейрона .

 

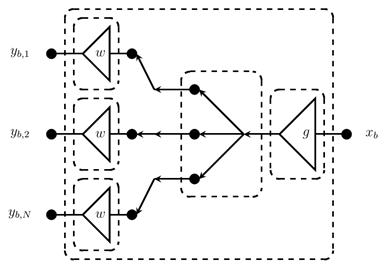
Рис. 4. Декомпозиция нейрона при обратном распространении ошибки.

Выходной сигнал нейрона формируется как результат прохождения суммы взвешенных входных сигналов через функциональный преобразователь:

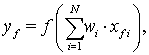                                                                                           (14)
где  – выходной сигнал при прямом прохождении,  – функция активации,  – -ый входной сигнал,  – -ый синоптический вес.

При обратном распространении сигнала поведение нейрона определяется поведением его составных элементов, рассмотренных ранее, в общем случае выходной сигнал определяется выражением 15.

                                                                                        (15)

где  – -ый выходной сигнал сети при обратном распространении,  – входной сигнал сети при обратном распространении,  – коэффициент усиления функционально преобразователя при обратном распространении,  – -ый синоптический вес. Учитывая поведение функционально преобразователя (14), выражение (15) принимает вид:

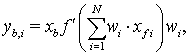                                                                                   (16)

Структурная схема нейрона при обратном распространении показана на рис. 4. В данном исследовании были реализованы различные виды нейронов, формируемые различными блоками функционального преобразования, входящими в состав нейрона.

Программная реализация

Для реализации прототипа программного обеспечения при помощи языка универсального моделирования (UML) [7] была разработана иерархия классов, в качестве языка программирования использовался Python, предоставляющий с одной стороны простую форму записи математических выражений, с другой – широкие возможности в области объектно-ориентированного программирования. Программная реализация разделена на две части – базовую и дополнительную. Базовая часть выполнена в качестве пакета и включает необходимую для работы приложения логику, однако не содержит инструментов ввода и вывода данных. Дополнительная часть предназначена для работы в интерактивном режиме в составе системы компьютерной математики Sage, пакете программ со свободной лицензией, объединенных единым пользовательским и программным интерфейсами. Дополнительная часть использует возможности Sage для ввода и вывода данных: генерация обучающих последовательностей, отображение графов, построение графиков и таблиц.

Результаты численного моделирования

Разработанный программный прототип был использован для численного моделирования применения нейронной сети для решения задачи аппроксимации и классификации входных данных.

 

 

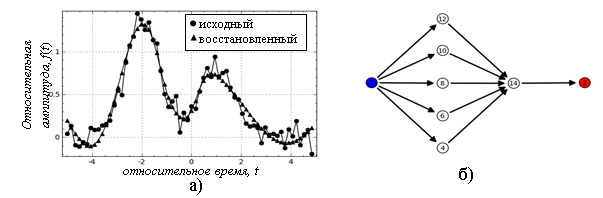
Рис 5. а) Входные данные и результат аппроксимации,

б) конфигурация нейронной сети, построенная прототипом программного обеспечения.

 

В качестве входного сигнала в задаче аппроксимации была использована аддитивная смесь суммы импульсов в форме функции Гаусса и шума:

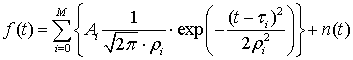                            ,                     (17)

где A_i – амплитуда импульса, ρ_i – параметр ширины импульса, τ_i – временная задержка прихода импульса, M – количество импульсов, n(t) – белый гауссовский шум. Практическое использование модель такого сигнала находит, например, в задачах идентификации точечных рассеивателей в сверхкороткоимпульсной радиолокации [8].

Входные данные показаны на рис. 5, a) точками, которые аппроксимированы ломанными для удобства восприятия. На рис. 5, б) представлен граф нейронной сети, построенный непосредственно с помощью средств разработанного программного прототипа.

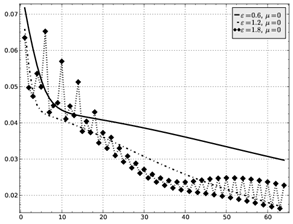
Зависимость среднеквадратической ошибки (СКО) за время обучения для метода градиентного спуска показана на рис. 6 (а), как видно из рисунка, увеличение исходного коэффициента скорости обучения  с 0.6 (непрерывная линия) до 1,2 (штрихпунктирная линия) позволяет несколько ускорить процесс обучения и добиться лучших результатов за меньшее время. Однако дальнейшее увеличение коэффициента скорости обучения приводит к слишком быстрой корректировке синаптических весов. Это приводит к тому, что веса осциллируют вокруг оптимальных значений, не достигая их, – аналогичный колебательный характер принимает и СКО.

 

  

а)                                                            б)

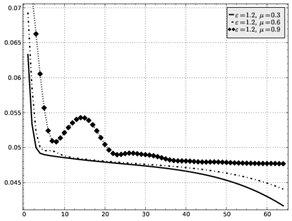
Рис. 6: Изменение среднеквадратической ошибки за время обучения для методов а) градиентного спуска, б) градиентного спуска с инерцией.

Для демонстрации эффекта инерции выбран коэффициент скорости обучения , затем проведено обучение сети при трех различных коэффициентах инерции . Результаты влияния эффекта инерции показаны на рис. 6 (б). Увеличение коэффициента инерции в ряде случаев приводит к незначительному изменению скорости обучения, причём дальнейшее увеличение приводит к негативному эффекту – дестабилизации процесса обучения сети в целом.

 

   

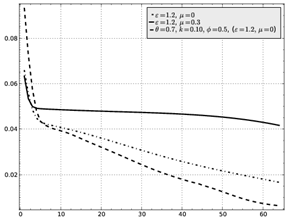
а)                                                             б)

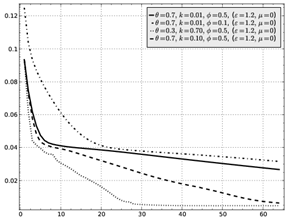
Рис. 7: Изменение среднеквадратической ошибки за время обучения
а) для метода Delta-Bar-Delta, б) всех представленных методов.

Наибольший интерес представляет метод Delta-Bar-Delta, результаты применения которого показаны на рис. 7 а). В [8] высказано предположение, что в большинстве случаев оптимальным набором параметров для данного метода являются следующие значения параметров формул (7, 8): , которым на рис. 7 соответствует непрерывная линия. Как видно из этого графика, отклонение параметров от оптимальных значений могут в конкретном случае приводить как к положительным, так и к отрицательным результатам. В случае чрезмерного уменьшения коэффициента скорости обучения (пунктирная линия) наблюдается значительное отставание в обучении. Уменьшение коэффициента γ, определяющего степень влияния градиентов ошибки, полученных в предыдущих эпохах и, одновременное, увеличение коэффициента , и, как следствие, ускорение роста коэффициента скорости, позволяет получить значительное улучшение качества обучения.

В зависимости от использованного метода обучения за некоторое количество итераций синаптические веса нейронной сети приближаются к оптимальным значениям. На рис. 5, а) треугольниками показан полученный выходной сигнал сети, аппроксимированный ломаной линией совместно с исходным сигналом.

Под классификацией понимают процедуру отнесения объекта (одного примера входных данных) к одному из двух или более классов. Для демонстрации применения нейронных сетей для решения этой задачи в работе рассматривается двумерный случай классификации. Практическое приложение этой задачи следующее. Посредством квадратурного демодулятора наблюдается один из двух узкополосных случайных процессов (СП). Известно, что плотность вероятности каждого из процессов описывается выражением:

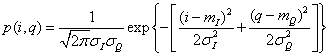                                                       (18)

где σ_I , σ_Q – дисперсии, а m_I , m_Q – математические ожидания составляющих СП.

 

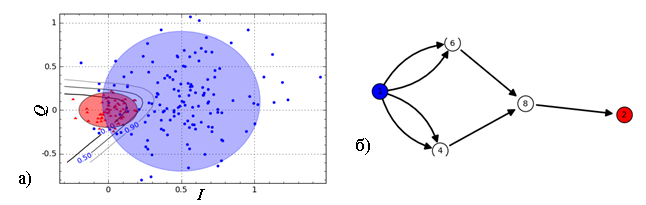
Рис 8. а) данные двух классов и граничные линии по уровням 0.1, 0.5 и 0,9,

б) нейронная сеть для решения задачи классификации.

 

В качестве входных данных для нейронной сети выступают координаты точек (рис. 8, а) на плоскости {I, Q}, принадлежащие одному из двух различаемых классов, соответствующих двум случайным процессам, параметры выражения (18) для которых различны. Выход сети должен определять принадлежность точки к первому или второму классу. Создана сеть с двумя входными нейронами, двумя нейронами в скрытом слое с сигмоидными функциями активации. Выходной нейрон сети так же имеет сигмоидную функцию активации, что необходимо для получения ограниченного по величине выходного сигнала. Предполагается, что выходной сигнал сети будет близок к нулю, если точка принадлежит к классу «A» и близок к единице, если точки принадлежит к классу «B». Созданная нейронная сеть показана на рис. 8, б.

Обучение сети проведено методом Delta-Bar-Delta [6] с коэффициентом скорости обучения 0,4, без коэффициента инерции и параметрами γ =0,3, φ=0,7, κ =0,5. На рис. 8, а) показана итоговая граница по уровню 0,5, которая принята при классификации. Подробное теоретическое решение этой задачи методом оптимального Байесовского классификатора представлено в монографии [2].

Заключение

В работе рассмотрены сети прямого прохождения сигнала, построенные на основе простых адаптивных элементов. Разработан прототип программного обеспечения, реализующий адаптивные элементы в рамках объектно-ориентированного подхода. Была разработана специализированная библиотека классов на языке Python для работы в среде Sage. В работе представлены результаты численного моделирования, проведенные с данным ПО. Примеры включают в себя обучение сетей, предназначенных для решения задач аппроксимации и классификации. Дальнейшее развитие данной методики состоит в расширении списка адаптируемых элементов, включение в него элементов с многомерными входами и выходами. Также большой практический интерес, по мнению авторов, представляет использование в адаптивных элементах методов второго порядка [5], которое потребует некоторого расширения и последующего обобщения рассмотренных подходов.

Литература

1.     M. H. Hassoun, Fundamentals of Artificial Neural Networks, The MIT Press, 1995, 511 p.

2.     С. Хайкин, Нейронные сети: полный курс, 2-е изд., испр. : Пер. с англ. –
М.: ООО «И.Д. Вильямс», 2006, 1104 стр.

3.     K. S. Narendra, K. Parthasarathy, Identification and Control of Dynamical Systems Using Neural Networks // IEEE Transactions on Neural Networks, Vol. 1, No. 1, March 1990, pp. 4–27.

4.     M.T. Hagan, H.B. Demuth, M.H. Beale, Neural Network Design, Martin Hagan, 2002, 736 p.

5.     R. Battiti, First- and Second-Order Methods for Learning: Between Steepest Descent and Newton's Method // Neural Computation, MIT, Vol. 4, No. 2, March 1992, pp. 141–166

6.     S. Samarasinghe, Neural Networks for Applied Sciences and Engineering: From Fundamentals to Complex Pattern Recognition, Auerbach Publications; 1 ed., 2006, 570 p.

7.     Г. Буч, Дж. Рамбо, А. Джекобсон, Язык UML. Руководство пользователя, Изд-во: «ДМК Пресс», 2007, 496 стр.

8.     Коновалюк М.А., Горбунова  А.А., Кузнецов Ю.В., Баев А.Б., Алгоритм извлечения информации из комплексного радиолокационного изображения сложной цели, 4-я всероссийская конференция «Радиолокация и радиосвязь», Москва, ИРЭ РАН, дек. 2010 г.