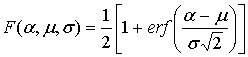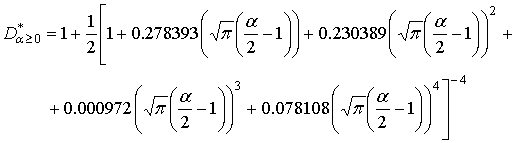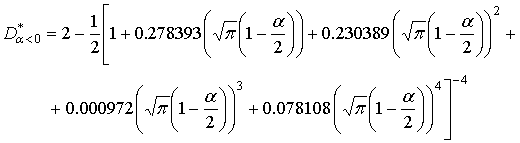УДК 621.391
УТОЧНЕНИЕ ОТНОШЕНИЯ МЕЖДУ ФРАКТАЛЬНОЙ РАЗМЕРНОСТЬЮ И СТЕПЕНЬЮ СПЕКТРА МОЩНОСТИ СИГНАЛА
С. А. Останин, А. М. Шайдук
Алтайский государственный университет, г. Барнаул
Получена
29 июля 2012 г.
Аннотация. Показана возможность уточнить отношение между фрактальной размерностью и степенью спектра мощности сигнала. Для аппроксимации использована функция распределения для нормального закона.
Ключевые слова: фрактальная размерность, спектр мощности.
Abstract. The possibility to increase the accuracy of the relationship between the fractal dimension and the degree of the power spectrum of the signal is proved. The distribution function for the normal law is used for approximation.
Keywords: fractal dimension, the power spectrum.
Фрактальную размерность
используют, например, в качестве меры сложности хаотических
сигналов или меры
статистического самоподобия случайных процессов [1-4] . Один из
способов оценки
фрактальной размерности ![]() сигнала
сигнала
![]() заключается
в использовании соотношения
заключается
в использовании соотношения
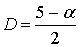 ,
(1)
,
(1)
где ![]() –
степень
частоты
–
степень
частоты ![]() спектра мощности
сигнала
спектра мощности
сигнала ![]() [5-8]:
[5-8]:
![]() (2)
(2)
при
![]() .
(3)
.
(3)
Этот способ нашел широкое применение при оценке фрактальной размерности радиосигналов [9], шумов различной природы [10], изображений [11-13] геологических поверхностей [14].
Поскольку связь спектра с
фрактальной размерностью ![]() в
виде
в
виде
![]() (4)
(4)
носит оценочный характер
(она является
асимптотическим решением интегрального уравнения [5-8,
10]), а простота
способа
определения фрактальной размерности сделала этот инструмент измерения
популярным,
представляет интерес выяснение границ применимости соотношения (4). Во
многих работах,
например [15-18], в ходе численного моделирования, была обнаружена
нелинейная
зависимость фрактальной размерности ![]() от
степени
от
степени ![]() спектра
мощности. Авторы работ [15-18] указывают
на существенно нелинейный характер зависимости вблизи границ диапазона
значений
параметра
спектра
мощности. Авторы работ [15-18] указывают
на существенно нелинейный характер зависимости вблизи границ диапазона
значений
параметра ![]() :
: ![]() . Однако
авторы не приводят выражения пригодного для аппроксимации зависимости
размерности
. Однако
авторы не приводят выражения пригодного для аппроксимации зависимости
размерности ![]() от
степени
от
степени ![]() спектра
сигнала, что ограничивает возможность использования полученных
результатов.
спектра
сигнала, что ограничивает возможность использования полученных
результатов.
Для решения задачи
уточнения
связи между фрактальной размерностью и степенью спектра мощности
сигнала был
выполнен численный эксперимент по генерации сигналов различной
фрактальной
размерности, определению их спектров мощности, степени ![]() спектра
сигнала, аппроксимации экспериментально полученной зависимости
спектра
сигнала, аппроксимации экспериментально полученной зависимости ![]() различными
функциями. Критерием выбора
оптимальной функции был минимум среднеквадратичного отклонения значений
аппроксимирующей функции от экспериментально полученных значений
фрактальной
размерности
различными
функциями. Критерием выбора
оптимальной функции был минимум среднеквадратичного отклонения значений
аппроксимирующей функции от экспериментально полученных значений
фрактальной
размерности ![]() .
.
Поскольку экспериментально
зависимости ![]() ,
полученные разными авторами, имели S-образный вид, в качестве
аппроксимирующих
функций для численных экспериментов были выбраны наиболее простые
сигмоиды:
,
полученные разными авторами, имели S-образный вид, в качестве
аппроксимирующих
функций для численных экспериментов были выбраны наиболее простые
сигмоиды:
функция Ферми (экспоненциальная сигмоида)
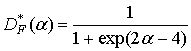 (5)
(5)
рациональная сигмоида
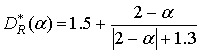 .
(6)
.
(6)
Кроме того, значения
фрактальной
размерности ![]() ,
вычисленные при различных значениях
степени
,
вычисленные при различных значениях
степени ![]() спектра
мощности, были аппроксимированы
функцией
спектра
мощности, были аппроксимированы
функцией
![]() ,
(7)
,
(7)
![]() имеет
вид функции распределения для нормального закона:
имеет
вид функции распределения для нормального закона:
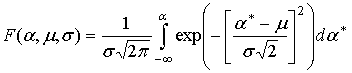 ,
(8)
,
(8)
где ![]() –
степень
спектра мощности,
–
степень
спектра мощности, ![]() –
положение центра симметрии
функций
–
положение центра симметрии
функций ![]() и
и ![]() на
оси
на
оси ![]() ,
, ![]() –
параметр,
определяющий максимальное значение производной функции
–
параметр,
определяющий максимальное значение производной функции ![]() .
.
Величина ![]() определяется
из условия равенства производной функции
определяется
из условия равенства производной функции ![]() в
точке перегиба (
в
точке перегиба (![]() )
)
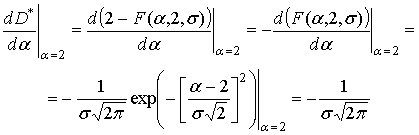 (9)
(9)
производной функции
размерности ![]() по
параметру
по
параметру ![]() :
:
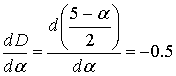 .
(10)
.
(10)
Приравнивая (9) и (10)
получаем
параметр ![]() :
:
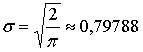 .
(11)
.
(11)
При ![]() фрактальная
размерность
фрактальная
размерность ![]() , что
соответствует размерности
броуновского движения, поэтому значение
, что
соответствует размерности
броуновского движения, поэтому значение ![]() определяется
из соотношения
определяется
из соотношения
![]() ,
(12)
,
(12)
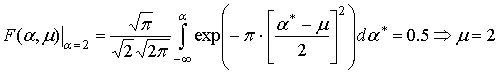 .
(13)
.
(13)
Таким образом, аппроксимирующая функция имеет вид:
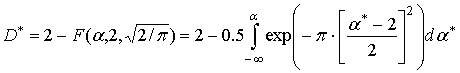 .
(14)
.
(14)
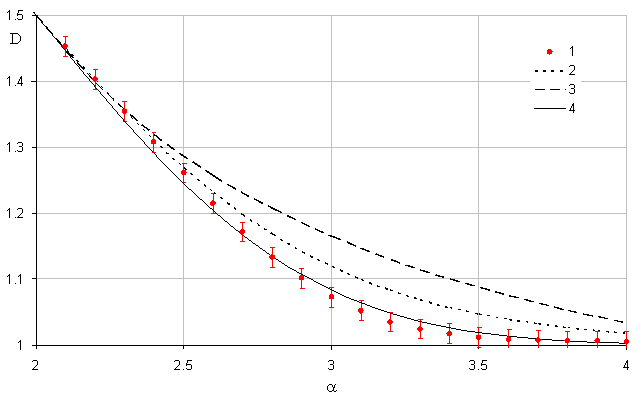
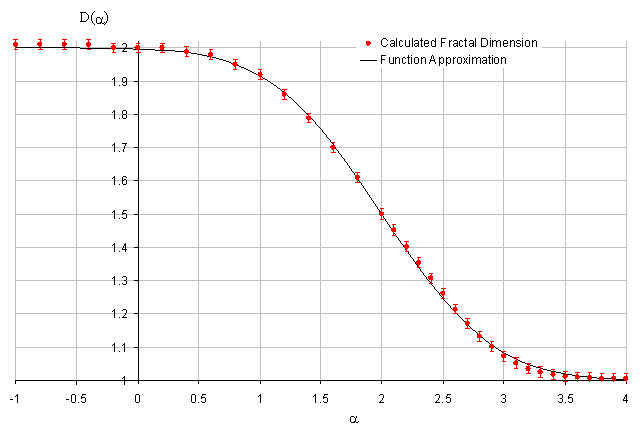
Рис. 1. Зависимость фрактальной размерности от параметра спектра:
1 – численный эксперимент ![]() ; 2 –
рациональная
сигмоида
; 2 –
рациональная
сигмоида ![]() ;
;
3 – функция Ферми ![]() ; 4 –
функция
; 4 –
функция ![]() .
.
В ходе численного
эксперимента генерировались сигналы ![]() различной
фрактальной
размерности со спектром вида
различной
фрактальной
размерности со спектром вида ![]() с
помощью программы,
реализованной на LabVIEW.
Фрактальная размерность модельных сигналов оценивалась с использованием
алгоритма Higuchi [19].
Фрагменты графиков зависимости фрактальной
размерности от параметра спектра
с
помощью программы,
реализованной на LabVIEW.
Фрактальная размерность модельных сигналов оценивалась с использованием
алгоритма Higuchi [19].
Фрагменты графиков зависимости фрактальной
размерности от параметра спектра ![]() показаны
на рисунке 1.
Из рисунка видно, что для аппроксимации следует использовать
функцию вида (7).
Среднеквадратичное отклонение (СКО) значений аппроксимирующей функции
показаны
на рисунке 1.
Из рисунка видно, что для аппроксимации следует использовать
функцию вида (7).
Среднеквадратичное отклонение (СКО) значений аппроксимирующей функции ![]() от
экспериментально полученных значений
фрактальной размерности
от
экспериментально полученных значений
фрактальной размерности ![]() является
наименьшим из
трех и составило величину около 0.005 (в единицах фрактальной
размерности).
является
наименьшим из
трех и составило величину около 0.005 (в единицах фрактальной
размерности).
Зависимость фрактальной
размерности ![]() модельного
сигнала
модельного
сигнала ![]() от
параметра спектра
от
параметра спектра ![]() и
аппроксимирующая функция
и
аппроксимирующая функция ![]() , для
диапазона значений
, для
диапазона значений ![]() показана
на рисунке 2. Величина
погрешности оценки экспериментально полученных значений
фрактальной
размерности
показана
на рисунке 2. Величина
погрешности оценки экспериментально полученных значений
фрактальной
размерности ![]() составила
величину 0.015. Для оценки
увеличения точности определения фрактальной размерности сигнала
при
использовании выражения (7) по сравнению с выражением (1),
построим функцию
разности
составила
величину 0.015. Для оценки
увеличения точности определения фрактальной размерности сигнала
при
использовании выражения (7) по сравнению с выражением (1),
построим функцию
разности ![]() :
:
![]() .
(15)
.
(15)