УДК 621.391
ИСПОЛЬЗОВАНИЕ ПОЧТИПЕРИОДИЧЕСКИХ ФУНКЦИЙ ДЛЯ СОЗДАНИЯ ХАОТИЧЕСКИХ СИГНАЛОВ
В. В. Егоров, М. С. Смаль
ОАО «Российский институт
мощного радиостроения
Получена 25 июня 2013 г.
Аннотация. Рассмотрен способ формирования хаотических сигналов с локализованным в заданной полосе частот спектром, изучены свойства таких сигналов и показана возможность их применения для передачи данных.
Ключевые слова: хаотический сигнал, полоса частот, передача данных.
Abstract: Method of forming chaotic signal with spectrum, localized in specified bandwidth is reviewed in the article. Properties of such signals are investigated and possibility of application for data communications is shown.
Key words: chaotic signal, bandwidth, data communications.
Одним из развивающихся в настоящее время направлений радиосвязи является использование хаотических сигналов для передачи данных. Известно множество подходов для создания таких сигналов [1,2]. Однако, большинство таких подходов содержат существенный недостаток, который затрудняет использование таких сигналов в реальных системах связи. Проблема состоит в том, что для практического использования необходимы сигналы, спектр которых локализован в строго заданных пределах по частоте, а формируемые хаотические сигналы, как правило, не локализованы в частотной области. Поэтому, задача создания хаотических сигналов с заданной шириной спектра является актуальной задачей.
Известно, что сумма двух периодических функций не всегда будет периодической функцией. Так, например функция вида:
![]()
является периодической только в том случае, если ![]() и
и ![]() являются соразмерными (имеют общее кратное).
Если
являются соразмерными (имеют общее кратное).
Если ![]() и
и ![]() не имеют общего кратного (например,
не имеют общего кратного (например, ![]() является целым, а
является целым, а ![]() иррациональным), то функция
иррациональным), то функция ![]() не имеет периода и называется
почтипериодической [3].
не имеет периода и называется
почтипериодической [3].
Рассмотрим сигнал следующего вида:
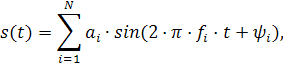
где ![]() параметры, от которых сильно зависит
вид
параметры, от которых сильно зависит
вид ![]() . Известно [3], что при определённом
выборе
. Известно [3], что при определённом
выборе ![]() сигнал
сигнал ![]() будет иметь стремящийся к
бесконечности период, а амплитудный спектр будет сосредоточен в ограниченной
полосе. Однако, в реальности использовать иррациональные числа для параметров
будет иметь стремящийся к
бесконечности период, а амплитудный спектр будет сосредоточен в ограниченной
полосе. Однако, в реальности использовать иррациональные числа для параметров ![]() нет возможности, так как все
используемые числа в вычислителях представлены с определённой точностью. Если в
этом случае они выбраны такими, что имеют очень большое общее кратное, то
функция
нет возможности, так как все
используемые числа в вычислителях представлены с определённой точностью. Если в
этом случае они выбраны такими, что имеют очень большое общее кратное, то
функция ![]() имеет очень большой период.
имеет очень большой период.
Рассмотрим задачу генерации хаотического сигнала в полосе телефонного
канала (300-3400 Гц). При использовании выражения можно
выбрать в качестве ![]() любое число,
любое число, ![]() выбрать постоянными, значения частот
выбрать постоянными, значения частот
![]() случайными числами, равномерно
распределенными на интервале [300, 3400], а фазы
случайными числами, равномерно
распределенными на интервале [300, 3400], а фазы ![]() – случайными числами в интервале [0,
– случайными числами в интервале [0, ![]() ].
].
Для моделирования было принято ![]() = 60.
= 60.
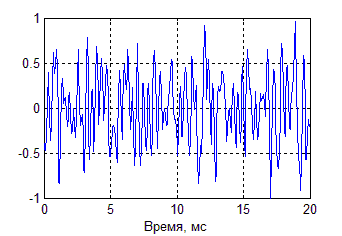
На рисунке 1 представлена реализация данного сигнала на длительности 20 мс.
Для определения периода такого сигнала было проведено моделирование, которое показало, что на интервале 10^9 отсчетов (при частоте дискретизации равной 16 кГц) использованная почтипериодическая функция не имеет периода.
На рисунке 2 представлен амплитудный спектр реализации данного сигнала на длительности 20 мс.
|
Рисунок 1. Реализация хаотического сигнала на длительности 20 мс. |
Рисунок 2. Амплитудный спектр реализации хаотического колебания. |
Из рисунка 2 видно, что спектр сигнала сосредоточен в заданной полосе. Поэтому отсутствует необходимость в дополнительной фильтрации такого сигнала после его формирования. При этом в независимости от реализации, основные спектральные составляющие не выходят за заданную полосу.
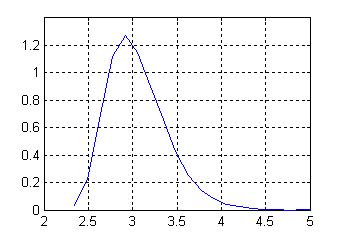
Для исследования эффективности использования передающей аппаратурой данного сигнала был исследован его пик-фактор, и построена выборочная плотность распределения, изображённая на рисунка 3. При этом, значение пик-фактора вычислялось на отрезках сигнала длительностью 20 мс, по формуле:

где ![]() максимальная мгновенная мощность,
максимальная мгновенная мощность, ![]() средняя мощность на длительности элементарной
посылки,
средняя мощность на длительности элементарной
посылки, ![]() номер посылки.
номер посылки.
Из рисунка 3. видно, что такой сигнал имеет в большинстве случаев пик-фактор не превышающий значений, свойственным классически используемым сигналам для передачи данных.
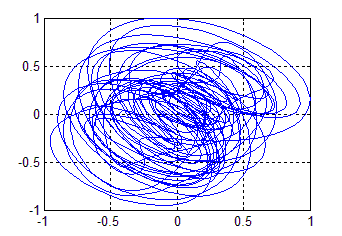
Для исследования хаотической структуры данного сигнала на рисунке 4 представлено отображение хаотического сигнала в координатах по Такенсу [1] с задержкой 1/8 мс на длительности 100 мс. Видно, что данному сигналу действительно характерны хаотические колебания.
|
Рисунок 3. Плотность распределения пик-фактора. |
Рисунок 4. Отображение хаотического сигнала в координатах по Такенсу с задержкой 1/8 мс. |
Использование таких сигналов для передачи данных возможно,
например, в режиме переключения сигналов. Тогда для передачи ![]() бит необходим ансамбль хаотических отрезков заданной
длительности объемом
бит необходим ансамбль хаотических отрезков заданной
длительности объемом ![]() , которые можно сформировать
предлагаемым способом с различными начальными условиями. На приёмной стороне
при этом необходимо, после установления синхронизации выделять отрезок сигнала,
соответствующий элементарной посылке и осуществлять демодуляцию на данном
отрезке времени одним из традиционных методов [4]. При этом при передаче данных
сигнал постоянно меняется и за время передачи данных ни разу не повторится. На
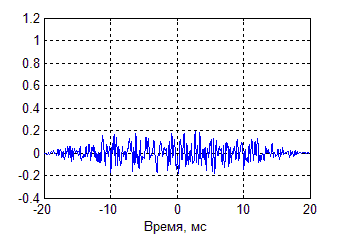
рисунке 5 изображена функция автокорреляции отрезка такого сигнала,
длительностью 20 мс, а на рисунке 6 функция взаимокорреляции двух отрезков
хаотического колебания. Из графиков видно, что для демодуляции можно использовать
корреляционный способ приема, так как автокорреляционная функция
характеризуется четким одиночным пиком, а взаимокорреляционная функция имеет
достаточно низкие значения. Кроме этого, такие свойства автокорреляционной
функции можно использовать для подстройки тактовой синхронизации.
, которые можно сформировать
предлагаемым способом с различными начальными условиями. На приёмной стороне
при этом необходимо, после установления синхронизации выделять отрезок сигнала,
соответствующий элементарной посылке и осуществлять демодуляцию на данном
отрезке времени одним из традиционных методов [4]. При этом при передаче данных
сигнал постоянно меняется и за время передачи данных ни разу не повторится. На
рисунке 5 изображена функция автокорреляции отрезка такого сигнала,
длительностью 20 мс, а на рисунке 6 функция взаимокорреляции двух отрезков
хаотического колебания. Из графиков видно, что для демодуляции можно использовать
корреляционный способ приема, так как автокорреляционная функция
характеризуется четким одиночным пиком, а взаимокорреляционная функция имеет
достаточно низкие значения. Кроме этого, такие свойства автокорреляционной
функции можно использовать для подстройки тактовой синхронизации.
|
Рисунок 5. Нормированная функция автокорреляции отрезка хаотического колебания |
Рисунок 6. Нормированная функция взаимокорреляции различных отрезков хаотического колебания.
|
Стоит отметить, что при рассмотренном выше способе выбора
номиналов частот присутствует вероятность их достаточно близкого расположения,
что может привести к увеличению энергии, сосредоточенной в определенной узкой
полосе, что в свою очередь может вызвать помехи сторонним станциям. Чтобы
избавиться от этого, можно использовать способ, который заведомо накладывает
ограничение на взаимное расположение частот, основанный на
применении методов порядковых статистик [5]. Суть способа заключается в том, что в единой
вычислительной схеме формируется список случайных частот, имеющих равномерное
распределение в выделенной полосе с условием, что расстояние между любыми двумя
соседними частотами, а также от границ полосы больше заданного ![]() :
:
Если каждая из ![]() равномерно распределенных величин
равномерно распределенных величин ![]() является равномерно распределенной в
интервале
является равномерно распределенной в
интервале ![]() , то закон распределения максимума
случайной величины
, то закон распределения максимума
случайной величины ![]() является законом распределения
является законом распределения ![]() ой порядковой статистики и
характеризуется следующей функцией распределения:
ой порядковой статистики и
характеризуется следующей функцией распределения:
![]()
Функция распределения случайной величины, расположенной в
интервале ![]() будет иметь вид:
будет иметь вид:
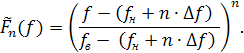
Получить значение ![]() можно получить из следующего
соотношения:
можно получить из следующего
соотношения:
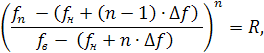
Где ![]() случайное число, равномерно
распределенное на интервале [0, 1].
случайное число, равномерно
распределенное на интервале [0, 1].
Тогда
![]()
Следующая величина ![]() будет являться
будет являться ![]() -ой порядковой статистикой и иметь
область определения
-ой порядковой статистикой и иметь
область определения ![]() , и её можно найти следующим образом:
, и её можно найти следующим образом:
![]()
Соответственно далее, для нахождения ![]() ой величины можно воспользоваться
правилом:
ой величины можно воспользоваться
правилом:
![]()
Полученный таким образом набор ![]() равномерно распределенных величин будет удовлетворять
условию (1) и отсортирован по убыванию.
равномерно распределенных величин будет удовлетворять
условию (1) и отсортирован по убыванию.
Применение данного способа для выбора номиналов частот на
каждом новом символе значительно снизит регулярность такого сигнала и уменьшит помехи
сторонним станциям. При этом начальные условия алгоритма формирования ![]() должны быть известны на приемной и
на передающей стороне. Кроме того, для надежной работы систем связи необходимо
поддерживать временную синхронизацию.
должны быть известны на приемной и
на передающей стороне. Кроме того, для надежной работы систем связи необходимо
поддерживать временную синхронизацию.
Таким образом, предложенный способ формирования хаотического сигнала легко реализуем на практике, позволяет на приёмной и передающей стороне создавать абсолютно идентичные хаотические сигналы, амплитудный спектр которых может быть задан в любой частотной полосе без использования дополнительной фильтрации.
1. Н.Н. Залогин, В.В. Кислов «Широкополосные хаотические сигналы в радиотехнических и информационных системах» - М. : Радиотехника, 2006.
2. F.C.M. Lau, C.K.Tse «Chaos-Based Digital Communication Systems» - Springer, 2003.
3. Г. Бор «Почти периодические функции» Пер. с нем. / Под ред. А.И. Плеснера. Изд. 2-е, стереотипное. – М. : Едиториал УРСС, 2005
4. Л.М.Финк. Теория передачи дискретных сообщений. — М. : Советское радио, 1970.
5. К.Г.Мазур, А.Н.Мингалев, М.С.Смаль. «Формирование частотно-временной матрицы с ограничениями на взаимное расположение частот». Вестник академии военных наук №3 (28) 2009.