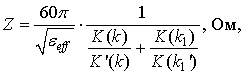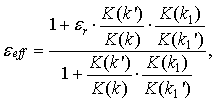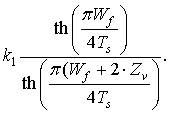УДК 621.396

фрактальная сверхширокополосная антенна на основе кругового монополя

 

Г. И. Абдрахманова

Уфимский государственный авиационный технический университет,

Universita degli studi di Trento

Получена 10 апреля 2013 г., после доработки – 12 августа 2013 г.

 

Аннотация. В статье рассмотрена задача проектирования сверхширокополосной антенны на основе фрактальной технологии. Представлены результаты исследований изменения характеристик излучения в зависимости от величины коэффициента масштаба и уровня итерации. Проведена параметрическая оптимизация геометрии антенны на соответствие требованиям коэффициента отражения. Размеры разработанной антенны составляют 34 × 28 мм², а диапазон рабочих частот – 3,09 ÷ 15 ГГц.

Ключевые слова: сверхширокополосная радиосвязь, фрактальная технология, антенны, коэффициент отражения.

Abstract: The development of a new ultra-wideband antenna on the basis of fractal technology is described in the paper. The research results on radiation characteristics changes depending on the value of scale factor and iteration level are presented. The parametric optimization of the antenna geometry for satisfying the reflection coefficient requirements was applied. The developed antenna size is 28 × 34 mm², and the bandwidth – 3,09 ÷ 15 GHz.

Key words: ultra-wideband radio communication, fractal technology, antennas, reflection coefficient.

 

1 Введение

На сегодняшний день  сверхширокополосные (СШП) системы связи представляют большой интерес для разработчиков и производителей телекоммуникационного оборудования, поскольку позволяют передавать огромные потоки данных с высокой скоростью в сверхширокой полосе частот на безлицензионной основе. Особенности передаваемых сигналов подразумевают отсутствие мощных усилителей и сложных компонентов обработки сигналов в составе приемо-передающих комплексов, но ограничивают дальность действия (5-10 м).

Отсутствие соответствующей элементной базы, способной эффективно работать со сверхкороткими импульсами, сдерживает массовое внедрение СШП технологии.

Приемо-передающие антенны являются одним из ключевых элементов, влияющих на качество передачи/приема сигналов. Основное направление патентов и исследований в области проектирования антенной техники для СШП устройств состоит в миниатюризации и снижении производственных затрат при обеспечении требуемых частотных и энергетических характеристик, а также в применении новых форм и структур.

Так, в [1] геометрия антенны построена на основе сплайна с прямоугольной П-образной прорезью в центре, что позволяет оперировать в СШП полосе с функцией заграждения WLAN-диапазона, размеры антенны – 45,6×29 мм². Ассиметричная Е-образная фигура размером 28×10 мм², расположенная на высоте 7 мм относительно проводящей плоскости         (50×50 мм²) выбрана в качестве излучающего элемента в [2]. Планарная монопольная антенна (22×22 мм²), спроектированная на основе прямоугольного излучающего элемента и лестничной резонансной структуры на оборотной стороне, представлена  [3].

2 Постановка задачи

Ввиду того, что круговые структуры могут обеспечивать довольно широкую полосу пропускания, упрощение конструкции, малые размеры и снижение затрат при производстве, в данной работе предлагается разработать СШП антенну на основе кругового монополя. Требуемый диапазон рабочих частот – 3,1 ÷ 10,6 ГГц по уровню -10 дБ коэффициента отражения S₁₁ [4],   (рис. 1). 

 

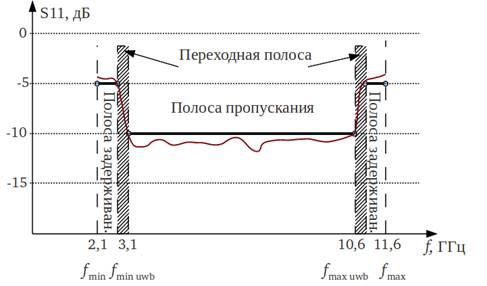
Рис. 1. Требуемая маска для коэффициента отражения S₁₁

 

С целью миниатюризации геометрия антенны будет модернизирована за счет применения  фрактальной технологии, что также позволит исследовать зависимость характеристик излучения от значения коэффициента масштаба δ и уровня итерации фрактала.

Далее поставлена задача оптимизации разработанной фрактальной антенны с целью расширения рабочего диапазона за счет изменения следующих параметров: длины центрального проводника (ЦП) компланарного волновода (КВ), длины плоскости земли (ПЗ) КВ, расстояния «ПЗ КВ - излучающий элемент (ИЭ)».

Моделирование антенны и численные эксперименты проводятся в среде «CST Microwave Studio».

3 Выбор геометрии антенны

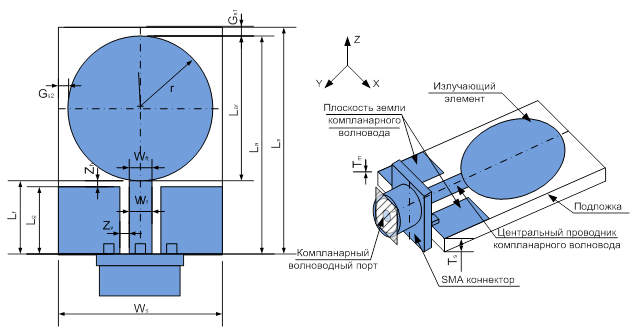
В качестве базового элемента выбран круговой монополь, размеры которого составляют четверть длины волны требуемого диапазона:

(1)

где L_ar – длина излучающего элемента антенны без учета ЦП; f_L – нижняя граничная частота, f_L = f _{min uwb} = 3,1·10⁹ Гц; с – скорость света, с = 3·10⁸ м/с².

Получаем L_ar = 24,19 мм ≈ 24 мм. Учитывая, что в качестве ИЭ выбран круг радиусом r = L_ar / 2 = 12 мм, и принимая первоначальную длину ЦП L_f  также равной r, получаем нулевую итерацию (рис. 2).

 

Рис. 2. Нулевая итерация антенны

 

Диэлектрическая подложка толщиной T_s и со значениями параметров      ε_s = 3,38, tg δ = 0,0025 используется как основа, на лицевой стороне которой размещены ИЭ, ЦП и ПЗ. При этом расстояния «ПЗ-ЦП» Z_v и «ПЗ-ИЭ» Z_h  приняты равными 0,76 мм. Значения остальных параметров, используемых в процессе моделирования, представлены в таблице 1.

 

Таблица 1. Параметры антенны (δ = 2)

Название	Описание	Формула	Значение
La	Длина антенны	2 ∙ r + Lf	36 мм
Wa	Ширина антенны	2 ∙ r	24 мм
Lf	Длина ЦП	r + 0,1	12,1 мм
Wf	Ширина ЦП		1,66 мм
Lg	Длина ПЗ	r – Ts	11,24 мм
Ls	Длина подложки	La + Gs	37 мм
Ws	Ширина подложки	Wa+ 2 ∙ Gs	26 мм
Gs1	Зазор подложки по вертикали		1 мм
Gs2	Зазор подложки по горизонтали		1 мм
Tm	Толщина металла		0,035 мм
Ts	Толщина подложки		0,76 мм
r	Радиус круга 0ой итерации		12 мм
r1	Радиус круга 1ой итерации	r /2	6 мм
r2	Радиус круга 2ой итерации	r1 /2	3 мм
r3	Радиус круга 3ей итерации	r2 /2	1,5 мм
εs	Диэлектрическая проницаемость		3,38

 

Антенна запитана при помощи компланарного волновода, состоящего из центрального проводника и плоскости земли, SMA-коннектора и расположенного перпендикулярно ему компланарного волноводного порта (КВП) (рис. 3).

 

Рис. 3. Компланарный волноводный порт и SMA-коннектор

 

Ширина ЦП W_f  рассчитана исходя из величины волнового сопротивления Z = 50 Ом:

(2)

где ε_eff  – эффективная диэлектрическая проницаемость:

(3)

K – полный эллиптический интеграл первого рода;         

	(4)
	(5)
	(6)

Фрактальность при построении антенны заключается в особом способе упаковки элементов: последующие итерации антенны образуются за счет размещения кругов меньшего радиуса в элементах предыдущей итерации. При этом коэффициент масштаба δ определяет, во сколько раз будут отличаться размеры соседних итераций. Данный процесс для случая δ = 2 представлен на рис. 4.

 

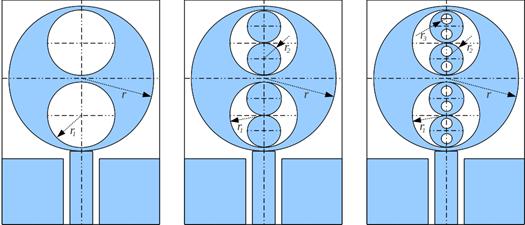
Рис. 4. Первая, вторая и третья итерации антенны (δ = 2)

 

Так, первая итерация получена за счет вычитания двух кругов радиусом r₁ из исходного элемента. Вторая итерация образована за счет размещения уменьшенных в два раза металлических кругов радиусом r₂ в каждом круге первой  итерации. Третья итерация аналогична первой, но радиус при этом r₃. В работе рассматривается вертикальное и горизонтальное расположение кругов.

3.1 Горизонтальное расположение элементов

Динамика изменения коэффициента отражения в зависимости от уровня итерации представлена на рис. 5 для δ = 2 и на рис. 6 для δ = 3. Каждому новому порядку соответствует одна дополнительная резонансная частота. Так, нулевой итерации в рассматриваемом диапазоне 0 ÷ 15 ГГц соответствуют 4 резонанса, первой итерации – 5 и т. д. При этом, начиная со второй итерации, изменения в поведении характеристик становятся менее заметными. 

Рис. 5. Зависимость коэффициента отражения от порядка итерации (δ = 2)

 

Суть моделирования заключается в том, что на каждом этапе из рассматриваемых характеристик выбирается та, которая определена как наиболее перспективная. В связи с этим введено правило:

Если превышение (разница) в диапазоне, где полки выше -10 дБ, невелико, то следует выбирать ту характеристику, у которой ниже полки в рабочем диапазоне (ниже -10 дБ), т. к. в результате оптимизации первые будут устранены, а вторые опущены еще ниже.

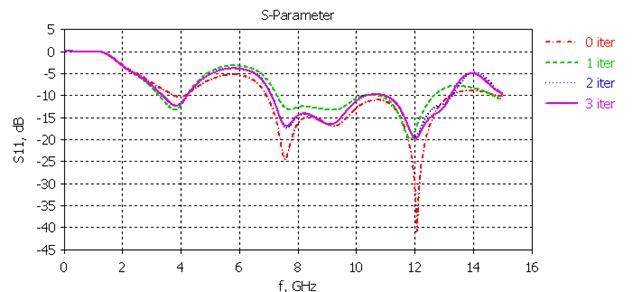
Рис. 6. Зависимость коэффициента отражения от порядка итерации (δ = 3)

На основании полученных данных и в соответствии с данным правилом для δ = 2 выбрана кривая, соответствующая первой итерации, для δ = 3 – второй итерации.

Далее предлагается исследовать зависимость коэффициента отражения от значения коэффициента масштаба. Рассмотрим изменение δ в диапазоне 2 ÷ 6 с шагом 1 в пределах первой и второй итераций (рис. 7, 8).

Интересное поведение графиков состоит в том, что, начиная с δ = 3, характеристики становятся более пологими и гладкими, количество  резонансов остается постоянным, а рост δ сопровождается повышением уровня S₁₁ в четных диапазонах и снижением – в нечетных.

Рис. 7. Зависимость коэффициента отражения от коэффициента масштаба для первой итерации (δ = 2; 3; 4; 5; 6)

 

В данном случае для обеих итераций выбрано значение δ = 6.

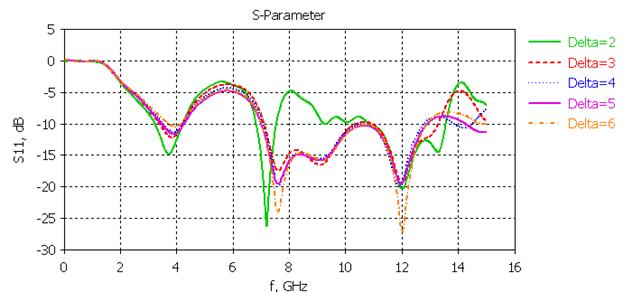
Рис. 8. Зависимость коэффициента отражения от коэффициента масштаба для второй итерации (δ = 2; 3; 4; 5; 6)

 

Таким образом, из четырех сравниваемых вариантов выбрана кривая, соответствующая второй итерации, δ = 6, поскольку она характеризуется самыми низкими полками и глубокими резонансами (рис. 9). 

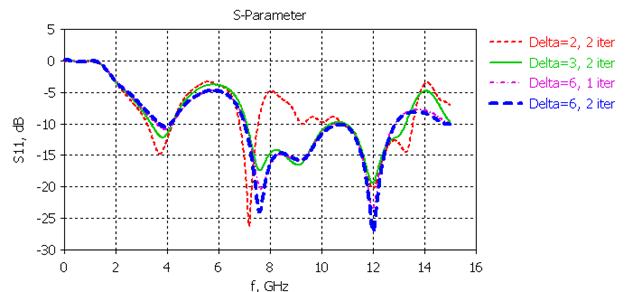
Рис. 9. Сравнение S₁₁ для четырех рассматриваемых геометрий антенны

3.2 Вертикальное расположение элементов

Динамика изменения коэффициента отражения в зависимости от уровня итерации для случая вертикального расположения кругов представлена на    рис. 10 для δ = 2 и на рис. 11 для δ = 3.

Рис. 10. Зависимость коэффициента отражения от порядка итерации (δ = 2)

 

На основании полученных данных и в соответствии с правилом для δ = 2 и δ = 3 выбрана кривая, соответствующая третьей итерации.

Рис. 11. Зависимость коэффициента отражения от порядка итерации (δ = 3)

 

Рассмотрение зависимости коэффициента отражения от значения коэффициента масштаба в пределах первой и второй итераций (рис. 12, 13) выявляет оптимальное значение δ = 6, как и в случае горизонтального расположения.

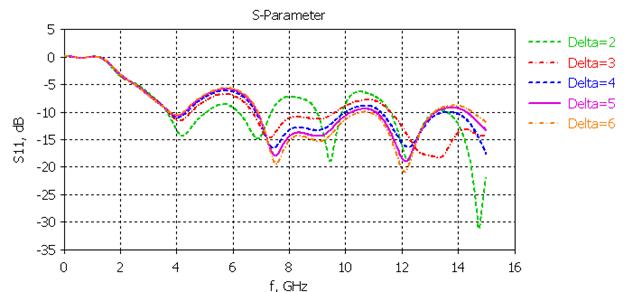
Рис. 12. Зависимость коэффициента отражения от коэффициента масштаба для первой итерации (δ = 2; 3; 4; 5; 6)

В данном случае для обоих итераций выбрано значение δ = 6, которое также представляет собой n-кратный фрактал, а значит, возможно, должен совмещать в себе особенности δ = 2 и δ = 3.

Рис. 13. Зависимость коэффициента отражения от коэффициента масштаба для второй итерации (δ = 2; 3; 4; 5; 6)

 

Таким образом, из четырех сравниваемых вариантов выбрана кривая, соответствующая второй итерации, δ = 6, как и в предыдущем случае (рис. 14).

Рис. 14. Сравнение S₁₁ для четырех рассматриваемых геометрий антенны

 

3.3 Сравнение

Рассматривая лучшие варианты вертикальной и горизонтальной геометрий, полученные в двух предыдущих подразделах, выбор останавливается на первой (рис. 15), хотя в данном случае разница между этими вариантами не столь велика. Рабочие диапазоны частот: 3,825÷4,242 ГГц и 6,969÷13,2 ГГц. Далее конструкция будет модернизирована с целью разработки антенны, функционирующей во всем СШП диапазоне.

 

Рис. 15. Сравнение S₁₁ для выбора итогового варианта

4 Оптимизация

В данном разделе рассматривается оптимизация антенны на основе второй итерации фрактала со значением коэффициента δ = 6. Варьируемые параметры представлены на рис. 2, а диапазоны их изменений – в таблице 2.

 

Таблица 2. Оптимизируемые параметры антенны

Название	Описание	Диапазон изменений, мм	Исх. значение, мм
∆Lf	Длина ЦП	∆Lf = [-6; -5;…+6]	0
Zh	Зазор горизонтальный	Zh = [0,1; 0,2;…0,76]	0,76
Gs2	Ширина зазора подложки по горизонтали	Gs = [0,5; 1;…6]	1,0

 

Процесс оптимизации включает в себя 3 шага в соответствии с тремя изменяемыми параметрами. Каждый последующий этап основан на ранее полученных результатах, т. е. изменение одного параметра сопровождается фиксированием значений всех остальных.

Шаг 1. Первым оптимизируемым параметром является длина ЦП L_f. Динамика изменения S₁₁ представлена на рис. 16.

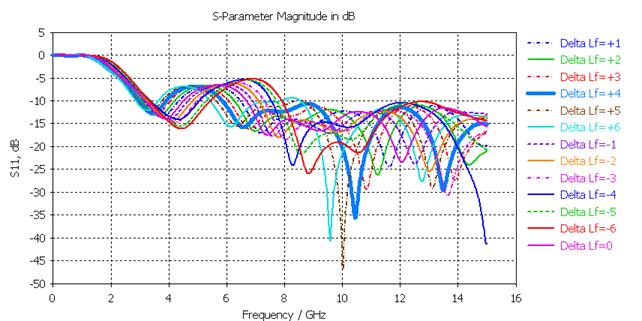
Рис. 16. Зависимость коэффициента отражения от величины ∆L_f

 

Увеличение длины ЦП сопровождается смещением резонансов в НЧ область, снижением полок в первом и третьем диапазонах и ростом – во втором. При ∆L_f  = +4 мм уровень первой полки один из самых низких, вторая полка гарантированно ниже -10 дБ, и тогда итоговая длина ЦП будет составлять 16,1 мм. 

Шаг 2. Второй параметр – горизонтальный зазор Z_h (расстояние «ПЗ-ИЭ») (рис. 17).

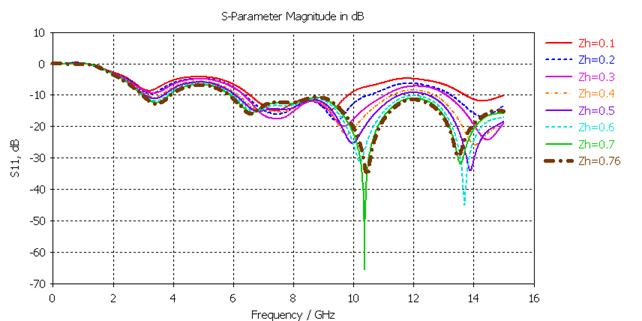
Рис. 17. Зависимость коэффициента отражения от величины Z_h

 

Увеличение зазора сопровождается снижением полок в первом и третьем диапазонах, а значит рассчитанное оптимальное значение Z_h­  = 0,76 мм.

Шаг 3. Третий параметр – ширина зазора подложки по горизонтали G_s2, которая также определяет изменение ширины ПЗ КВ. 

Чем шире ПЗ, тем резонансы все более смещаются в область НЧ, полки во всех диапазонах опускаются, четные резонансы становятся глубже (рис. 18). Наименьшее значение G_s2, при котором обеспечивается СШП диапазон, составляет 5 мм.  

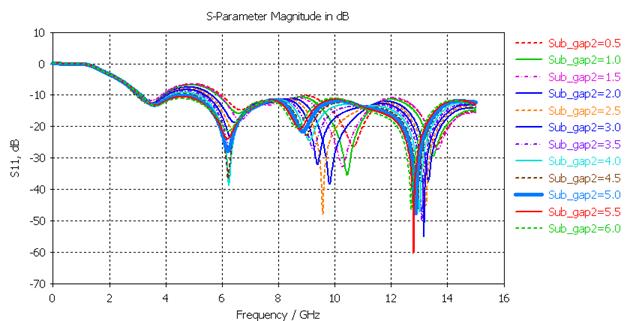
Рис. 18. Зависимость коэффициента отражения от величины G_s2

 

На данном этапе оптимизация закончена, полоса частот разработанной антенна составляет 3,09÷15 ГГц по уровню -10 дБ при размерах 34×28 мм²  (рис. 19). Рассчитанные параметры антенны сведены в общую таблицу 3.

 

   

а)                                                              б)

Рис. 20. Внешний вид антенны: а) лицевая сторона; б) оборотная сторона

 

На рис. 20 приведены характеристики, отражающие динамику изменения S₁₁ по шагам и доказывающие обоснованность каждого последующего действия. В таблице 4 показаны резонансные и граничные частоты, используемые далее для расчета поверхностных токов и диаграммы направленности.

 

Таблица 3. Рассчитанные параметры антенны

Название	Исходное значение, мм	Конечное значение, мм
∆Lf	0	+4,0
Zh	0,76	0,76
Gs2	1,0	5,0

 

Рис. 20. Динамика пошагового изменения S₁₁

 

Таблица 4. Резонансные и граничные частоты

Частота, ГГц	S11, дБ
3,09	-9,9651098
3,6	-13,133208
6,195	-27,910472
8,85	-21,613615
10,6	-12,503542
12,87	-47,745235

 

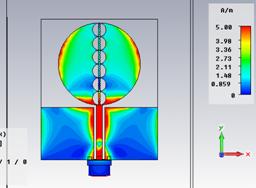
Распределение поверхностных токов антенны на резонансных и граничных частотах СШП диапазона представлено на рис. 21, а диаграммы направленности – на рис. 22.

 

       

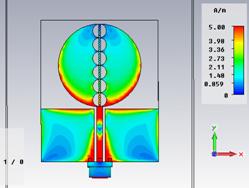
а) 3,09 ГГц                                  б) 3,6 ГГц

       

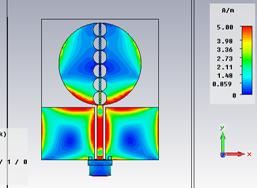
в) 6,195 ГГц                                г) 8,85 ГГц

       

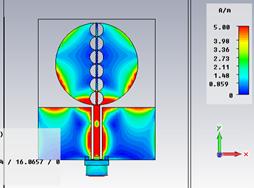
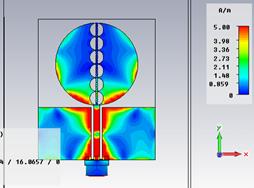
д) 10,6 ГГц                                  е) 12,87 ГГц

Рис. 21. Распределение поверхностных токов

 

                  

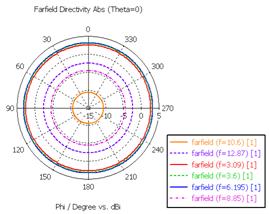
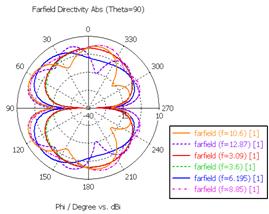
а) F(φ), θ = 0°                                           б) F(φ), θ = 90°

      

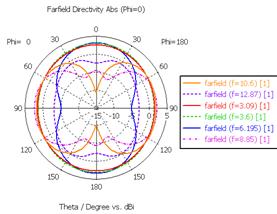
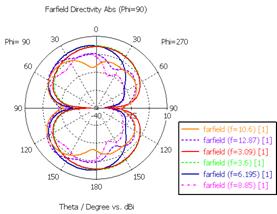
в) F(θ), φ = 0°                                           г) F(θ), φ = 90°

Рис. 22. Диаграммы направленности в полярной системе координат

5 Заключение

В данной работе представлен новый метод проектирования СШП антенн на основе применения фрактальной технологии. Данный процесс подразумевает два этапа. Первоначально определяется геометрия антенны посредством выбора соответствующего коэффициента масштаба и уровня итерации фрактала. Далее к полученной форме применяется параметрическая оптимизация на основе изучения влияния размеров ключевых компонентов антенны на характеристики излучения.

Установлено, что с ростом порядка итерации количество резонансных частот увеличивается, а возрастание коэффициента масштаба в пределах одной итерации характеризуется более пологим поведением S₁₁ и постоянством резонансов (начиная с δ = 3).

Разработанная антенна обеспечивает качественный прием сигналов в полосе частот 3,09 ÷ 15 ГГц по уровню S₁₁ < -10 дБ. Помимо этого антенна характеризуется малыми размерами 34×28 мм², а следовательно может быть успешно применена в СШП приложениях.

6 Благодарности

Исследование поддержано грантом Европейского Союза «Erasmus Mundus Action 2», также А. Г. И. благодарит профессора Paolo Rocca за полезное обсуждение.

 

Литература

1. L. Lizzi, G. Oliveri, P. Rocca, A. Massa. Planar monopole UWB antenna with UNII1/UNII2 WLAN-band notched characteristics. Progress in Electromagnetics Research B, Vol. 25, 2010. – 277-292 pp.

2. H. Malekpoor, S. Jam. Ultra-wideband shorted patch antennas fed by folded-patch with multi resonances. Progress in Electromagnetics Research B, Vol. 44, 2012. – 309-326 pp.

3. R.A. Sadeghzaden-Sheikhan, M. Naser-Moghadasi, E. Ebadifallah, H. Rousta, M. Katouli, B.S. Virdee. Planar monopole antenna employing back-plane ladder-shaped resonant structure for ultra-wideband performance. IET Microwaves, Antennas and Propagation, Vol. 4, Iss. 9, 2010. – 1327-1335 pp.

4. Revision of Part 15 of the Commission’s Rules Regarding Ultra-Wideband Transmission Systems, Federal Communications Commission, FCC 02-48, 2002. – 118 p.