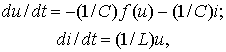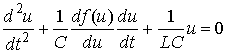УДК 621.372, 532.59
ИССЛЕДОВАНИЕ ЭФФЕКТИВНОСТИ СОВРЕМЕННЫХ ЧИСЛЕННЫХ МЕТОДОВ ПРИ АНАЛИЗЕ АВТОКОЛЕБАТЕЛЬНЫХ ЦЕПЕЙ
А. М. Пилипенко, В. Н. Бирюков
Южный федеральный университет
Получена 27 июля 2013 г.
Аннотация. В работе проведено тестирование численных методов анализа автоколебательных цепей во временной области. В качестве тестовой задачи выбрано дифференциальное уравнение автогенератора с полигональной нелинейностью. Показана высокая эффективность метода трапеций для анализа автоколебательных цепей.
Ключевые слова: автогенератор, колебательные цепи, обыкновенные дифференциальные уравнения, погрешность решения.
Abstract. In the paper the testing of numerical methods for analysis of oscillating systems in the time domain is held. As a test problem selected oscillator differential equation with arbitrary polygonal nonlinearity. The high efficiency of trapezoidal method for analysis of self-oscillating circuits is shown.
Keywords: oscillating circuits, nonlinear differential equations, error analysis.
Введение
В настоящее время разработано большое количество численных методов решения обыкновенных дифференциальных уравнений (ОДУ), с помощью которых осуществляется моделирование радиотехнических цепей и устройств во временной области. В программах схемотехнического моделирования (SPICE, Multisim, Microcup) и системах автоматизации инженерных расчетов (Mathcad, Matlab) используются методы Гира, основанные на многошаговых формулах дифференцирования назад, одношаговые явные и неявные многостадийные методы Рунге-Кутта, а также ряд других методов [1-3]. Выбор численного метода предоставляется пользователю. В свою очередь, методы обладают различными свойствами (точность, устойчивость и вычислительная сложность) и неправильный выбор метода решения ОДУ может привести к резкому увеличению времени анализа цепи, получению качественно неверного результата или вообще к сбою программы. Указанные проблемы наиболее характерны для численного анализа автоколебательных цепей во временной области, поскольку системы ОДУ, описывающие такие цепи, часто оказываются одновременно осциллирующими и жесткими [3]. В этом случае эффективность того или иного метода численного решения ОДУ требует дополнительного исследования.
Целью настоящей работы является проведение сравнительного анализа и оценка эффективности современных методов численного решения ОДУ для достаточно важного класса цепей – генераторов гармонических (ангармонических) колебаний.
Основной моделью для анализа периодических автоколебаний в задачах радиоэлектроники является уравнение Ван-дер-Поля [4], которое получается из дифференциального уравнения автогенератора при аппроксимации вольт-амперной характеристики (ВАХ) нелинейного элемента кубическим полиномом. Аналитическое решение уравнения Ван-дер-Поля для установившегося режима известно [5], но область практического применения этого решения весьма ограничена, поскольку, как правило, точность аппроксимации ВАХ нелинейных элементов полиномом третьей степени оказывается низкой. В то же время иные дифференциальные уравнения автогенератора имеют только приближенные решения [6].
В данной работе в качестве тестовой задачи для проведения сравнительного анализа и оценки эффективности современных методов численного решения ОДУ предлагается использовать модель автогенератора, в которой ВАХ нелинейного элемента аппроксимируется кусочно-линейной функцией. Указанная модель позволяет, с одной стороны, уменьшить погрешность аппроксимации ВАХ, а с другой – получить точное решение для наиболее важного для практики стационарного режима [7].
1. Уравнение автогенератора
Схема замещения автогенератора, приведенная на рис. 1, содержит линейные емкость C и индуктивность L, а также нелинейный резистивный элемент, ВАХ которого описывается нелинейной функцией iG = f (u).
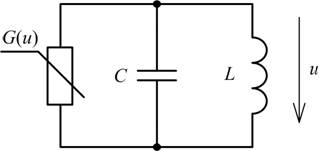
Рис. 1. Схема замещения автогенератора.
Система ОДУ автогенератора для переменных состояния [8] имеет вид
где u – напряжение на емкости и i – ток индуктивности.
Дифференциальное уравнение для напряжения может быть записано в виде
Если дифференциальная проводимость G(u) = df (u)/du на каком-либо участке ВАХ принимает отрицательное значение, то в LC-контуре могут возникать автоколебания. При аппроксимации ВАХ нелинейного элемента iG = f(u) кубическим степенным многочленом уравнение (2) называется уравнением Ван-дер-Поля и для установившегося режима известны его аналитические решения [9]. К сожалению, решение в явном виде получить не удается, и существуют только эталонные численные решения, специально вычисленные с высокой точностью для некоторых параметров уравнения и начальных данных [5]. Кроме того, точное решение (2) при аппроксимации ВАХ полиномом третьей степени практического значения не имеет, поскольку точность аппроксимации мала.
2. Аналитическое решение уравнения автогенератора
Для получения аналитического решения уравнения автогенератора для стационарного режима можно использовать кусочно-линейную аппроксимацию ВАХ, погрешность которой при увеличении количества линейных участков уменьшается практически неограниченно. При выбранном типе нелинейности на каждом участке изменения функции u(t), который соответствует линейному участку ВАХ, решение можно записать в виде
где
; Gk – дифференциальная
проводимость на k-линейном участке ВАХ; 
; N – число линейных участков
ВАХ.
Для определения постоянных интегрирования А1,k, А2,k и интервала времени Тk, соответствующего
прохождению k-го линейного участка, необходимы три условия. Двумя из них
являются значения f(u) на границах k-го участка, третьим
служит, следующая из первого закона коммутации [8], непрерывность производной
du/dt при переходе от одного линейного участка ВАХ к
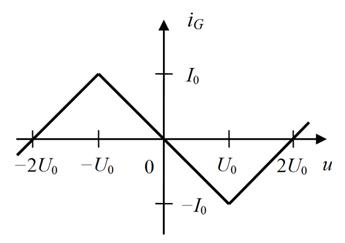
другому. Например, в простейшем случае симметричной ВАХ, показанной на рис. 2, система алгебраических
уравнений для определения стационарного решения на полупериоде колебания t
[0, T / 2] имеет вид [7]
где начальное значение uk(0) = – U0 выбрано произвольно, поскольку начало отсчета не влияет на стационарное решение [5].
В случае симметричной ВАХ определять решение на
всем периоде колебания нет необходимости, поскольку при t[T / 2, T ] оно повторяет с
противоположным знаком решение на первой половине периода. Выражение (3) может
использоваться и при комплексных значениях pk. В этом случае для
упрощения решения системы (4) целесообразно определять только одну комплексную
постоянную интегрирования, приняв вторую комплексно сопряженной первой.
Рис. 2. ВАХ нелинейного элемента.
Точные стационарные решения системы (1),
полученные с помощью соотношений (3) и (4) показаны на рис. 3. Решение на
рис. 3, а получено при L = 1 Гн, С = 1 Ф,
U0 = 1 В, I0 = 4 А, на
рис. 3, б – при L = 1 Гн, С = 1 Ф,
U0 = 1 В, I0 = 0.05 А.
Форма полученных колебаний определяется добротностью LC-контура 
, где 
и 
. Для случая, показанного
на рис. 3, а, 
и имеют место
релаксационные колебания. Рис. 3, б соответствует значение 
, при котором решение
уравнения автогенератора представляет собой ангармоническое колебание
(колебание близкое по форме к гармоническому, но в общем случае описывающееся
негармонической функцией).
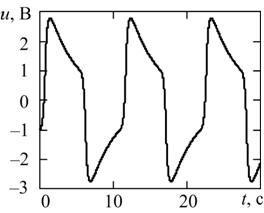
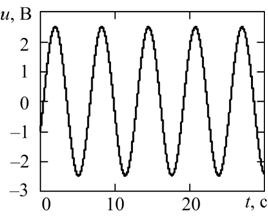
(а) (б)
Рис. 3. Решение уравнения автогенератора для релаксационных колебаний (а) и ангармонических колебаний (б).
3. Тестирование численных методов решения ОДУ
В данной работе проведен сравнительный анализ следующих численных методов: метода трапеций, Гира и RADAU5. В качестве тестовой задачи, использовалась система (1), где f(u) представлена в виде симметричной кусочно-линейной функции (см. рис. 2). Краткое описание указанных методов приведено ниже.
Метод трапеций является одним из простейших неявных методов
численного решения ОДУ, но в настоящее время этот метод используется во всех
программах схемотехнического моделирования. Популярность
метода трапеций объясняется тем, что его область устойчивости совпадает с левой
полуплоскостью комплексной плоскости, кроме того метод трапеций имеет второй
порядок точности, что приемлемо для практических задач (погрешность численного
решения уменьшается пропорционально квадрату временного шага). Метод трапеций
для системы ОДУ 
, 
описывается
следующей формулой (разностной схемой)
, (5)
где h – временной шаг, n – целое неотрицательное число, xn и xn + 1 –приближенные значения решения системы ОДУ в моменты времени tn и tn + 1 = tn + h соответственно.
Метод Гира является основным методом анализа переходных процессов в программах схемотехнического моделирования. Метод Гира реализуется с помощью довольно сложного алгоритма, обеспечивающего автоматический выбор шага и порядка метода в зависимости от заданной погрешности. Разностные схемы метода Гира представляет собой неявные многошаговые формулы, известные как формулы дифференцирования назад (ФДН- или BDF-методы), которые были впервые введены Кёртисом и Хиршфелдером (1952 г.) и подробно описаны в работе [1]. На практике используются BDF-методы, имеющие порядок точности от первого до шестого.
Метод RADAU5 является одним из наиболее перспективных методов типа Рунге-Кутта [2]. Метод RADAU5 основан на трехстадийном (s = 3) полностью неявном методе Рунге-Кутта пятого порядка точности (p = 5). Отметим, что метод трапеций также является неявным методом Рунге-Кутта, для которого число стадий s = 1 и порядок точности p = 2. Размерность системы алгебраических уравнений, полученных с помощью неявного метода Рунге-Кутта, будет равна s∙m, где m – размерность заданной системы ОДУ (порядок сложности цепи). Таким образом, при использовании метода RADAU5, требуется решать систему алгебраических уравнений, размерность которой в три раза больше размерности системы ОДУ заданной цепи.
Для оценки эффективности описанных выше численных методов применим методику, предложенную в работе [10]. В качестве критерия эффективности метода будем использовать точность оценки основных параметров генерируемого колебания – частоты и амплитуды. Текущие относительные погрешности оценки частоты и амплитуды соответственно определяются с помощью следующих соотношени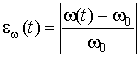й
и 
,
где ω(t) и Am(t) – оценки частоты и амплитуды генерируемого колебания, полученные из решения системы (1) численными методами; ω0 и Am0 – точные значения частоты и амплитуды автоколебания, полученные на основании соотношений (3) и (4).
На рис. 4 и рис. 5 приведены временные диаграммы относительных погрешностей оценки частоты и амплитуды стационарного колебания автогенератора при различных добротностях колебательной системы (Q = 20 и Q = 100). Решение системы уравнений (1) осуществлялось описанными выше численными методами при заданном максимально шаге решения hmax = T / 1000, где T = 2π / ω0 – период автоколебаний.
Точные значения частоты и амплитуды генерируемых колебаний:
а) при Q = 20 (L = 1 Гн, С = 1 Ф, U0 = 1 В, I0 = 0.05 А):
ω0 = 0.99989149411682 рад/с, Am0 = 2.475477417618089 В;
б) при Q = 100 (L = 1 Гн, С = 1 Ф, U0 = 1 В, I0 = 0.01 А):
ω0 = 0.99999565970188 рад/с, Am0 = 2.475416990116814 В.
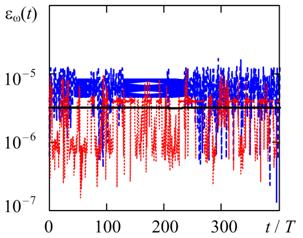
(а) (б)
Рис. 4. Текущие относительные погрешности оценки частоты методами трапеций (черная линия), Гира (синяя кривая) и RADAU5 (красная кривая) при Q = 20 (а) и Q = 100 (б).
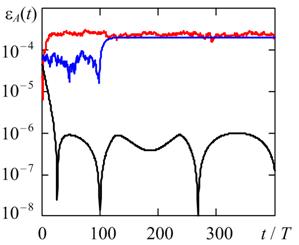
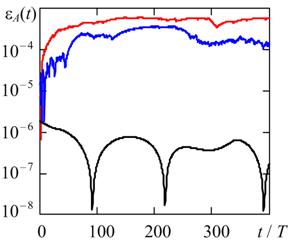
Рис. 5. Текущие относительные погрешности оценки амплитуды методами трапеций (черная линия), Гира (синяя кривая) и RADAU5 (красная кривая) при Q = 20 (а) и Q = 100 (б).
Для оценки частоты колебаний использовалась линейная интерполяция численного решения в точках изменения знака u(t), для оценки амплитуды – квадратичная в точках локальных экстремумов. Интервал наблюдения выбран таким, чтобы показать наступление стационарного режима.
Из рис. 4 видно, что для всех рассмотренных численных методов погрешность оценки частоты имеет одинаковый порядок величины. В свою очередь, как следует из рис. 5, погрешность оценки амплитуды для метода трапеций примерно на два порядка меньше аналогичных погрешностей методов Гира и RADAU5.
Выводы
Проведено тестирование численных методов анализа автоколебательных цепей во временной области для обеспечения достоверных и наиболее точных результатов анализа. В качестве тестовой рассмотрена задача анализа автогенератора, в котором ВАХ нелинейного элемента аппроксимируется кусочно-линейной функцией. Данная задача важна для практики, поскольку разрыв производных решения в колебательных системах возможен не только вследствие выбора способа аппроксимации ВАХ, но и возникает при анализе высокодобротных цепей, работающих в режиме отсечки тока [11].
Полученные результаты подтверждают тезис о том, что на практике при анализе радиотехнических автоколебательных цепей метод трапеций (по-видимому, вследствие своей Р-устойчивости [12]) оказывается не менее эффективным, чем методы высоких порядков [13]. Контроль точности метода осуществлялся не по погрешности определения переменной, а по погрешностям определения параметров стационарного процесса. Полученные результаты дополняют известные аналитические оценки свойств численных методов решения дифференциальных уравнений для осциллирующих систем.
Работа выполнена при поддержке стипендии Президента Российской Федерации молодым ученым и аспирантам, осуществляющим перспективные научные исследования по приоритетным направлениям модернизации российской экономики (СП-398.2012.5).
Литература
1. Хайрер Э., Нёрсетт С., Ваннер Р. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи. М.: Мир, 1990, 512 с.
2. Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. М.: Мир, 1999, 685 с.
3. Пилипенко А. М. Бирюков В. Н. Гибридные методы решения обыкновенных дифференциальных уравнений жестких и/или колебательных цепей // Радиотехника, 2011, № 1, c. 11–15.
4. Кузнецов А. П., Кузнецов С. П., Рыскин Н. М. Нелинейные колебания. Учеб. пособие для вузов. М.: Изд-во физ-мат. литературы, 2002, 292 с.
5. Гужев Д. С., Калиткин Н. Н. Уравнение Бюргерса – тест для численных методов // Математическое моделирование, 1995, Т.7, №4, с. 99 – 127.
6. Abd El-Halim Ebaid Approximate periodic solutions for the non-linear relativistic harmonic oscillator via differential transformation method // Communications in Nonlinear Science and Numerical Simulation, 2010, v. 15, №. 7, pp. 1921-1927.
7. Бирюков В.Н., Гатько Л.Е. Точное стационарное решение уравнения автогенератора // Нелинейный мир, 2012, Т. 10, № 9, с. 613-616.
8. Попов В. П. Основы теории цепей. Учебник для студ. вузов. 6-е изд., стереотип. М.: Высшая школа, 2007, 575 с.
9. Андронов А. А., Витт А. А., Хайкин С. Э. Теория колебаний. М.: Гос. изд-во физ-мат. литературы, 1959, 915 с.
10. Бирюков В. Н., Пилипенко А. М. Ковтун Д.Г. Оценка точности численного анализа генератора гармонических колебаний во временной области // Радиотехника, 2011, № 9, С. 104-107.
11. Pietrenko W., Janke W., Kazimierczuk A. K. Large-signal time-domain simulation of class E amplifier // IEEE International Symposium in Circuits and Systems, ISCAS 2002, v.5, p. 21 – 24.
12. Petzold L. R., Jay L. O., Yen J. Numerical solution of highly oscillatory ordinary differential equations // Acta Numerica, 1997, p. 437 – 483.
13. Жук Д. М., Маничев В. Б., Ильницкий А. О. Методы и алгоритмы решения дифференциально-алгебраических уравнений для моделирования динамики технических систем и объектов // Проблемы разработки перспективных микро- и наноэлектронных систем – 2008. Сб. научных трудов / под ред. А. Л. Стемпковского. – М.: ИППМ РАН. 2008, c. 109 – 113.