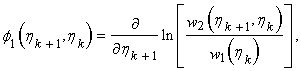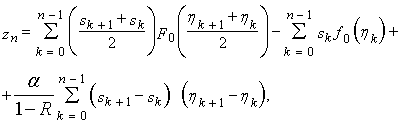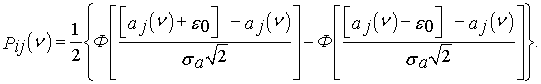ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ И ФИЗИЧЕСКИХ ОБЪЕКТОВ В ПРОБЛЕМЕ ФУНКЦИОНИРОВАНИЯ РАДИОЛОКАЦИОННЫХ СИСТЕМ В УСЛОВИЯХ ЕСТЕСТВЕННЫХ И ПРЕДНАМЕРЕННЫХ ПОМЕХ
А. Б. Борзов 1, Р. П. Быстров 2, В. Л. Меньшиков 3,
В. Н. Пожидаев 2, В. Б. Сучков 1, В. А. Черепенин 2
1 Московский государственный технический университет им. Н.Э. Баумана
2 Институт радиотехники и электроники им. В.А. Котельникова РАН
3
Министерство обороны РФ
Статья получена 24 июля 2015 г.
Аннотация. Рассматриваются результаты исследований особенностей взаимодействия электромагнитных волн с проводящими объектами в радиолокационных сценах. Приводятся особенности вторичного излучения радиоволн объектами при исследованиях резонансов поглощения дециметровых, сантиметровых и миллиметровых волн РЛС обнаружения объектов для повышения помехозащищенности. Предложена поляризационная матрица рассеяния модели объекта со статистическими неровностями поверхности. Анализируются методы обработки радиолокационных сигналов на различных уровнях мешающих помех.
Ключевые слова: электромагнитные волны, вторичное излучение, матрица рассеяния, естественные помехи, поглощение радиоволн, обнаружение объекта.
Abstract. In the article, the results of studies of EM waves interaction with conductive objects the radar scenes, are considered. Some peculiarities of secondary emission of radio waves by the objects in absorbtion resonances studies at decimeter, centimeter and millimeter wavelengths are investigated. A polarization scattering matrix model of an object with statistically rough surface is proposed. In conclusion, some methods of radar signal processing at different interfering noise levels are discussed.
Keywords: electromagnetic waves, secondary radiation, scattering matrix, natural disturbance, absorption of radio waves, radar systems, object detecting.
1. АНАЛИЗ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЙ ВЗАИМОДЕЙСТВИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН С ПРОВОДЯЩИМИ ОБЪЕКТАМИ В РАДИОЛОКАЦИОННЫХ СЦЕНАХ
В данном подразделе на основе научных вопросов, относящихся к решению проблемы оценки компоненты многократных взаимодействий радиоволн с проводящими объектами, приводятся результаты исследований резонансов поглощения дециметровых, сантиметровых и миллиметровых волн РЛС обнаружения объектов для повышения помехозащищенности.
Проблему оценки компоненты многократных взаимодействий волн с элементами полигональной модели радиолокационной сцены для повышения помехозащищенности можно решать путем комбинированного применения метода геометрической оптики, для построения лучевых трубок и метода физической оптики, позволяющего вычислить поле рассеяния в дальней зоне [1].
1.1. Проблема оценки компоненты многократных взаимодействий волн
Физический смысл теории заключается в том, что поле, падающее на некоторый треугольный элемент поверхности, не рассеивается в окружающее пространство, а переотражается по законам геометрической оптики в направлении другого треугольного элемента и служит источником возбуждения на нем вторичных электромагнитных волн.
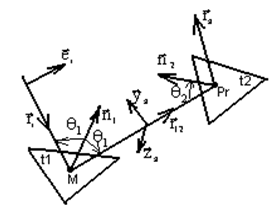
Рис. 1.1. Схема переотражения электромагнитной волны между двумя треугольниками
Эти электромагнитные
волны, рассеиваясь в направлении приемника, создают в апертуре приемной антенны
дополнительное поле. Основной задачей является определение амплитуды и поляризации
электромагнитной волны, переотраженной с первого треугольного элемента на второй
(рис 1.1). Падающая на первый треугольник t1 плоская волна под углом
падения к нормали ![]() отражается из его средней точки
M под тем же углом в направлении на треугольник t2. Плоская
волна с поляризационным вектором
отражается из его средней точки
M под тем же углом в направлении на треугольник t2. Плоская
волна с поляризационным вектором ![]() при отражении изменяет
направление вектора поляризации. При этом целесообразно представить
поляризационный вектор отраженной волны в локальном базисе:
при отражении изменяет
направление вектора поляризации. При этом целесообразно представить
поляризационный вектор отраженной волны в локальном базисе: ![]() , учитывая, что координаты вектора
, учитывая, что координаты вектора ![]() в этом базисе не изменяются при
отражении. Следует также отметить, что вектор
в этом базисе не изменяются при
отражении. Следует также отметить, что вектор ![]() принадлежит
плоскости отражения волны (и соответственно совпадающей с ней плоскостью
падения), а вектор
принадлежит
плоскости отражения волны (и соответственно совпадающей с ней плоскостью
падения), а вектор ![]() -ей ортогонален. Характер
отражения от первого треугольника в геометрооптическом представлении носит
поляризационно зависимый характер, т. е. для соответствующих поляризационных
компонент отраженного поля
-ей ортогонален. Характер
отражения от первого треугольника в геометрооптическом представлении носит
поляризационно зависимый характер, т. е. для соответствующих поляризационных
компонент отраженного поля ![]() и
и ![]() существуют различные коэффициенты
отражения, зависящие от электродинамических параметров и угла падения. Тогда с
учетом закона сохранения энергии целесообразно представить поле, отраженное с
первого треугольника в направлении на второй в виде совокупности двух плоских
волн, соответствующих вертикально и горизонтально поляризованным составляющим:
существуют различные коэффициенты
отражения, зависящие от электродинамических параметров и угла падения. Тогда с
учетом закона сохранения энергии целесообразно представить поле, отраженное с
первого треугольника в направлении на второй в виде совокупности двух плоских
волн, соответствующих вертикально и горизонтально поляризованным составляющим:
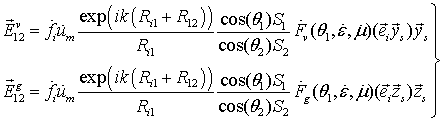 (1.1)
(1.1)
где ![]() -
расстояние от передающей системы до средней точки первого треугольника;
-
расстояние от передающей системы до средней точки первого треугольника; ![]() - расстояние между средней точкой первого
треугольника M и точкой пересечения отраженного
луча со вторым треугольником Pr;
- расстояние между средней точкой первого
треугольника M и точкой пересечения отраженного
луча со вторым треугольником Pr;
![]() - угол падения на первый треугольник;
- угол падения на первый треугольник; ![]() - угол падения переотраженного луча на
второй треугольник;
- угол падения переотраженного луча на
второй треугольник; ![]() - площади первого и второго
треугольников;
- площади первого и второго
треугольников; ![]() - значение функции
направленности передающей антенны в направлении на первый треугольник.
- значение функции
направленности передающей антенны в направлении на первый треугольник.
Далее задача рассеяния поля вторым треугольником с источниками возбуждения в форме соотношений (1.1) решается с использованием метода физической оптики. При этом общее выражение для поля рассеяния в дальней зоне второго треугольника можно представить в следующем виде:
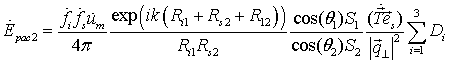 , (1.2)
, (1.2)
где ![]() -
значение функции направленности приемной антенны в направлении на второй
треугольник;
-
значение функции направленности приемной антенны в направлении на второй
треугольник; ![]() - расстояние от приемной системы до точки
пересечения переотраженного луча со вторым треугольником Pr;
- расстояние от приемной системы до точки
пересечения переотраженного луча со вторым треугольником Pr; ![]() -
векторный множитель, функционально зависящий от поляризации волны падающей на
второй треугольник, а также от электродинамических параметров первого и
второго треугольников;
-
векторный множитель, функционально зависящий от поляризации волны падающей на
второй треугольник, а также от электродинамических параметров первого и
второго треугольников; ![]() - проекция вектора
- проекция вектора ![]() на плоскость второго треугольника;
на плоскость второго треугольника;![]() - определяется соотношением [1,2]
- определяется соотношением [1,2]
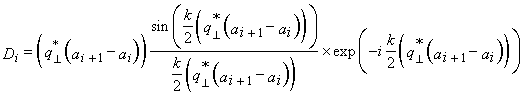 , (1.3)
, (1.3)
где ![]() -
проекция вектора
-
проекция вектора ![]() ; k = 2π/λ
– волновое число.
; k = 2π/λ
– волновое число.
Результирующий вклад от переотражений между элементами сложных объектов определяется когерентным суммированием вторичных полей рассеяния для тех треугольных элементов, которые участвуют в переотражениях. Компонента суммарного рассеянного поля, характеризующая вклад переотражений между треугольными элементами, принадлежащих как сложному объекту, так и фоновым образованиям, определяется по аналогии с уже рассмотренным методом с той лишь разницей, что вторичное рассеянное поле от фоновых образований определяется с использованием приведенных выше соотношений и носит стохастический (случайный) характер.
Так, в случае, если элемент отражения (ЭО) является частью детерминированной металлической поверхности, для определения его комплексных коэффициентов отражения применяется метод Гордона.
1.2. Исследование резонансов поглощения дециметровых, сантиметровых и миллиметровых волн РЛС обнаружения объектов для повышения помехозащищенности
Целесообразно отметить, что для повышения помехозащищенности РЛС могут быть выбраны частотные точки резонанса как с максимальным, так и с минимальным поглощением радиоволн.
Достоинство резонансных точек с максимальным поглощением электромагнитных волн заключается в том, что здесь они могут обеспечивать максимальную помехозащищенность РЛС, так как становится сложнее обнаружить как по основному, так и по боковым лепесткам ДНА из-за достаточно малых для обнаружения мощностей. Недостатком является то, что при функционировании РЛС с соответствующим энергетическим потенциалом снижается их дальность действия из-за сильного поглощения зондирующего сигнала
Если для РЛС выбирать рабочие частоты в «окнах прозрачности», то указанные достоинства и недостатки диаметрально противоположны вышеуказанным.
Отсюда вытекает вывод, что рабочую частоту РЛС необходимо выбирать как из условий требуемой работоспособности РЛС, так и из условий функционирования в обеспечении прикладных задач.
Опираясь на результаты исследований распространения радиоволн в атмосфере и отражательных характеристик наземных объектов, отметим те, которые наиболее приемлемы для обоснования лучшей помехозащищенности РЛС при выполнении задач обнаружения [3]. Это прежде всего особенности вторичного излучения радиолокационных отражателей и поверхностей объектов и физических тел.
1.2.1. Задачи радиолокационного обнаружения
Среди многочисленных применений современная радиолокация наиболее широкое применение в мирных целях получила в радионавигации и, в первую очередь, в авиации при вождении самолетов на близкие и дальние расстояния, в морском флоте для навигации кораблей. Радиолокационные системы используются также для рекогносцировки и картографирования местности, прогноза погоды, служат средством обнаружения грозовых фронтов и зон выпадения осадков [4-14].
В военном деле радиолокация незаменима при обнаружении наземных, воздушных и космических объектов в дневное и ночное время, в том числе в тумане, облаках, дымовых завесах и в дождях. Широкой областью применения радиолокации является выполнение функций опознавания «свой – чужой» самолетов и различного рода техники с несакционированным доступом. Одной из достаточно сложных задач радиолокации является точное определение координат различных объектов (самолетов, кораблей, гусеничной и автомобильной техники), что необходимо для управления зенитной и полевой артиллерией, а также для наведения управляемого оружия.
Правильное обнаружение должно иметь место в условиях интенсивных активных и пассивных помех с учетом влияния среды распространения радиоволн.
1.2.2. Особенности вторичного излучения радиоволн объектами
При активной радиолокации объектов производится анализ сигналов вторичного излучения, возникающего в результате отражения, рассеяния, резонансного отклика вторичного излучения или дифракции радиоволн при взаимодействии зондирующего сигнала РЛС с исследуемыми объектами. Отражающий объект при облучении РЛС становится источником вторичного излучения. Если проводимость, диэлектрическая или магнитная проницаемость материала изменяется достаточно резко, то при облучении поверхности раздела двух сред часть энергии будет переизлучаться в обратном направлении. В зависимости от качества и состояния поверхности возможны следующие механизмы переизлучения: зеркальное отражение, диффузное рассеяние и резонансное излучение.
Так, зеркальное отражение возникает при облучении больших гладких поверхностей, размеры которых много больше длины волны. В случае шероховатых поверхностей отражение будет зеркальным, если выполняется критерий Релея и высота неровностей Dh удовлетворяет условию:
![]() . (1.4)
. (1.4)
Диффузное рассеяние наступает при облучении поверхности с неровностями порядка длины волны l. В случае наличия шероховатостей поверхности объекта может возникать рассеянное излучение радиоволн вследствие различной пространственной ориентации его отдельных элементов. При этом рассеянное излучение подчиняется закону диффузного рассеяния (закону Ламберта).
Резонансным излучением обладают малые объекты с размерами неровностей порядка l/2. Резонансное излучение чаще всего наблюдается в метровом диапазоне радиоволн. При этом резонансное излучение имеет максимальную интенсивность, если наибольший размер элемента объекта совпадает по направлению с вектором электрической поляризации излучения РЛС.
Дифракция радиоволн имеет место в случаях, когда размеры объекта равны или меньше длины волны излучения. Дифракционное поле может накладываться на падающую электромагнитную волну, что может приводить к искажению поля вблизи такого объекта.
1.2.3. Эффективные поверхности рассеяния объектов
ЭПР одиночных объектов. Интенсивность вторичного излучения от объекта зависит от особенностей формы объекта, характеристик ее поверхности и эффективной ее площади, определяющей диаграмму направленности вторичного излучения. При анализе вторичного излучения необходимо различать наличие: одиночных объектов (одиночные самолеты, корабли и др.), групповых объектов (несколько самолетов, кораблей и др.), распределенных в пространстве объектов (земную и водную поверхности и зоны выпадения дождя и снега).
Для расчета возможной
дальности обнаружения объектов необходимо знание интенсивности вторичного
излучения на входе приемной антенны радиолокатора. Интенсивность этого
излучения зависит от направленности приемной антенны, ее ориентации
рассеивающих или отражающих свойств объекта, что определяется соотношением
величины шероховатости поверхностей объекта по сравнению с длиной волны
излучения. При этом точное определение этой интенсивности затруднительно на
расстояниях, характерных для промежуточной и ближней зон излучения. Так как
форма объекта является обычно достаточно сложной, то для описания
характеристик вторичного излучения таких объектов вводят так называемую
эффективную поверхность рассеяния ![]() (ЭПР). При этом под
эффективной поверхностью рассеяния объекта сложной формы понимается такая
площадь плоской поверхности
(ЭПР). При этом под
эффективной поверхностью рассеяния объекта сложной формы понимается такая
площадь плоской поверхности ![]() , перпендикулярная к
прямой передатчик-приемник, которая создает у раскрыва приемной антенны
радиолокатора амплитуду сигнала вторичного излучения объекта, равную реальному
сигналу от объекта сложной формы. ЭПР является сложной функцией длины волны
излучения, коэффициента направленного действия антенны.
, перпендикулярная к
прямой передатчик-приемник, которая создает у раскрыва приемной антенны
радиолокатора амплитуду сигнала вторичного излучения объекта, равную реальному
сигналу от объекта сложной формы. ЭПР является сложной функцией длины волны
излучения, коэффициента направленного действия антенны.
Расчет величины s является сложной и некорректной задачей, так как определение функции направленного действия объекта не имеет строгого решения.
В физике используется несколько иное выражение для эффективной поверхности рассеяния объекта sэпр, которую принято называть полной эффективной площадью рассеяния.
При этом определении реальная мощность облучения объекта имеет вид:
 ,
(1.5)
,
(1.5)
где П1 – плотность
потока мощности, подводимая радиолокационным передатчиком к его антенне; П2
– плотность потока мощности вторичного излучения, создаваемая объектом у
раскрыва антенны радиолокатора; R- расстояние между приемником и передатчиком; ![]() элемент
телесного угла в направлении на радиолокатор.
элемент
телесного угла в направлении на радиолокатор.
Отметим, что sэпр связана с величиной s следующим соотношением:
 . (1.6)
. (1.6)
Благодаря свойству обратимости передающих и приемных антенн увеличение направленности антенн также эффективно при приеме, как и при передаче. При этом коэффициент направленного действия антенны приемного устройства имеет то же значение, что при передаче и может быть найден по формуле:
![]() , (1.7)
, (1.7)
где c - множитель, изменяющийся в пределах 0,5-0,8 и учитывающий неравномерность поля в раскрыве антенны; А - геометрическая площадь приемной антенны. Произведение Аc = А э носит название эффективной поглощающей площади приемной ( передающей) антенны:
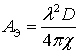 . (1.8)
. (1.8)
Умножение А на
вектор Умова - Пойтинга дает мощность, извлекаемую приемной антенной из
энергии вторичного изучения объекта. Для зеркал типа параболоидов вращения
площадь раскрыва антенны равна ![]() , вследствие чего
максимальный коэффициент ее направленного действия антенны будет:
, вследствие чего
максимальный коэффициент ее направленного действия антенны будет:
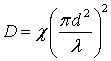 . (1.9)
. (1.9)
Если радиолокатор
облучает цель с расстояния R,
то на поверхность цели будет падать плотность потока энергии ![]() , где PS- мощность излучения передатчика.
, где PS- мощность излучения передатчика.
В случае изотропности объекта мощность вторичного излучения в не поглощающей среде у приемной антенны радиолокатора будет равна:
![]() , (1.10)
, (1.10)
где А э - эффективная площадь приемной антенны радиолокатора.
Таким образом, s и А э определяются в (1.10) приближенно, и дальность действия РЛС определяется с той же точностью, с какой известны значения s и Аэ. Поэтому в ряде случаев для различных объектов используются экспериментально найденные числовые величины эффективных поверхностей рассеяния или отражения, что может повышать точность определения дальности РЛС.
В последние годы был разработан универсальный метод определения ЭПР на основе математического моделирования объектов сложной пространственной формы [15]. Этот метод позволяет при известной форме и электрических характеристиках объекта с достаточной для практики точностью рассчитать его ЭПР, что подтверждается результатами экспериментальных исследований.
Хотя эффективная поверхность рассеяния цели является сложной функцией многих переменных и не поддается точному определению, для приближенных оценок дальности радиолокатора можно пользоваться средними величинами ЭПР объектов в диапазоне сантиметровых волн, приведенными в табл. 1.1.
Таблица 1.1. Средние значения величин ЭПР объектов в диапазоне сантиметровых волн
|
Объекты |
Величина ЭПР, м2 |
|
Крылатая ракета Истребитель Легкий бомбардировщик Тяжелый бомбардировщик В 52 ТУ 95 В1-В F117 В2 Головка баллистической ракеты Крейсер Траулер Малая подвозная лодка в надводном положении Катер Рубка подводной лодки Бронетраспортер Танк Автомобиль |
0,3-0,5 1-5 15- 25 50-70 125 125 1 0,1 0,01 0,001 14000 750 140 100 1 5-30 6-9 6-8 |
Однако максимальные значения ЭПР объектов могут различаться от средних на 10-15 дБ. ЭПР реальных объектов зависит от длины волны излучения, поляризации, азимута, угла места, материала объекта и его формы, а также от направления движения объекта.
Так, например, на основании расчетов ЭПР с применением геометрической теории дифракции (ГТД) и физической теории дифракции (ФТД) с учетом формы и материала американского самолета F-14 без радиопоглощающего материала (РПМ) было установлено, что величины s были равными: на волне 1 см 40280 м2, на волне 10 см- 264 м2 и на волне 15 см. -142 м2 [15].
Для примера на рис. 1.2 и 1.3 приведены горизонтальные диаграммы обратного рассеяния самолета – бомбардировщика на волне 10 см и самолета - невидимки В-2 на волне 3 см. Рис. 1.3 был получен методом когерентного суммирования при угле подхода 15 ° в секторе углов 0-90° при линейной вертикальной поляризации излучения [16,17]. Динамический диапазон изменения ЭПР самолета В-2 составил от - 46,5 до +12дБ.

Рис. 1.2. Горизонтальная диаграмма обратного рассеяния самолета бомбардировщика на волне 10 см
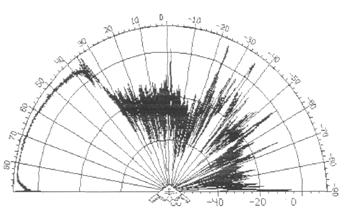
Рис. 1.3. Диаграмма ЭПР самолета типа " Стелс".
Видно, что с передних ракурсов самолет В-2 практически невидим, однако сбоку и сверху в пределах углов 35-90° ЭПР самолета достаточна для его обнаружения. Поэтому при определении дальности действия РЛС необходимо иметь круговые диаграммы ЭПР, рассчитанные методом математического моделирования с учетом формы и материала объектов в диапазонах радиоволн существующих РЛС. Такие расчеты указывают на возможность обнаружения самолетов и объектов с малыми ЭПР, защищенными радиопоглощающими материалами (РПМ).
Вопросам исследований ЭПР воздушных и наземных объектов в данной работе посвящаются специальные разделы, поэтому на этом вопросе остановились только на общей и краткой характеристике ЭПР объектов как с применением, так и без применения методов «Стелс».
Но это, важно для того, чтобы дать ориентировочные оценки дальности действия различных РЛС, работающих на сантиметровых и метровых волнах, при известных средних величинах ЭПР, что является задачей дальнейших рассмотрений.
Вторичные поля рассеяния распределенных объектов. К числу распределенных по пространству объектов относятся земная, водная поверхности, дождевые и грозовые облака. Такие распределенные объекты существенно превышают ширину диаграммы направленности приемной антенны радиолокатора. Распределенные в пространстве объекты делятся на поверхностные и объемные.
При радиолокации поверхностных целей радиолокатор принимает отражения от различных участков земной или водной поверхностей при наклонной дальности распространения. Если радиолокатор определяет дальность до объекта методом повторяющихся импульсов, то возникает необходимость оценок эффективной поверхности рассеяния. В случае земной или водной поверхности импульс излучения облучает последовательно во времени эту поверхность по наклонной дальности. Подобная ситуация возникает, например, при полете самолета над такой поверхностью. В этом случае по определению эффективной поверхности рассеяния она должна быть перпендикулярна к направлению излучения передатчика.
Пусть в точке А расположен радиолокатор (см. рис. 1.4), который облучает импульсами земную поверхность. Пусть ширина диаграммы антенны в горизонтальной плоскости a, максимальная наклонная дальность R, высота полета аппарата H, q- угол места относительно горизонта. Допустим, что абвг- сечение импульсом лучей АБ и АГ.

Рис. 1.4. К определению ЭПР земной поверхности с самолета
Тогда из геометрических соотношений следует, что облучаемая площадь поверхности будет:
![]() , (1.11)
, (1.11)
где R - максимальная дальность;![]() -
длительность импульса;
-
длительность импульса; ![]() = ÐАВГ. Эффективная площадь участка
земной поверхности будет иметь следующий вид:
= ÐАВГ. Эффективная площадь участка
земной поверхности будет иметь следующий вид:
![]() , (1.12)
, (1.12)
где Г- эффективный коэффициент отражения земной поверхности.
Так как R>>H, то из (1.112) получается следующее выражение для эффективной площади рассеяния земной поверхности при локации ее с летательного аппарата и высоты полета Н:
![]() .
(1.13)
.
(1.13)
Из (1.13) следует, что эффективная отражающая поверхность, как и следовало ожидать, пропорциональна длительности импульса, высоте полета, величине коэффициента отражения и ширине диаграммы направленности в азимутальной плоскости.
При выпадении осадков радиолокатор наблюдает сигналы рассеяния от взвешенных в воздухе и двигающихся частиц (дождя или снега), представляющих собой распределенные по пространству объемные цели. Для того чтобы оценить интенсивность отраженной или рассеянной энергии от дождя в направлении радиолокатора необходимо выделить в пространстве некоторый объем и вычислить отраженную им энергию. При взаимодействии электромагнитной волны с частицами дождя будет происходить поглощение падающей волны и появление рассеянного излучения. При этом отраженные от дождя сигналы зависят от поляризации излучения, интенсивности дождя, скорости падения капель и распределения капель дождя по размерам. Пренебрегая эффектами поглощения в дожде и распределением капель по размерам получим выражение, определяющее эффективность отражения сигналов от дождя и от объекта, которое имеет такой вид:
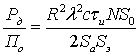 ,
(1.14)
,
(1.14)
где Пд и По - мощности, отраженные от слоя дождя и от объекта; сtи - протяженность волнового пакета; R- расстояние до объекта и слоя дождя; l- длина волны излучения; Sa -эффективная площадь антенны радиолокатора; Sэ - эффективная площадь рассеяния объекта; Sо - эффективная площадь капли; N- число капель дождя в единице объема.
Формула (1.14) позволяет приближенно оценивать интенсивность сигналов, обусловленных отражением от дождя. Следует заметить, что более строгое решение задачи об интенсивности отражения радиоволн от слоя дождя является также приближенным, так как дождь неоднороден в пространстве и во времени. Существует около 9 различных типов дождей, распределение капель по размерам в которых является неизвестным. Кроме этого капли дождя изменяют свою форму при падении на земную поверхность. Поэтому более точное решение задачи носит также характер приближенных оценок.
Вместе с тем, следует заметить, что ослабление радиосигналов в дожде и сильные отражения от слоя дождя способны маскировать цели, подлежащие обнаружению с помощью радиолокатора.
Проиллюстрируем формулу (1.14)
на конкретном примере. Пусть радиолокатор на волне 3 см облучает слой дождя на расстоянии 30 км. Пусть длительность импульса составляет 0,7 мкс, дождь -
однородный в пространстве с диаметром капель 2 мм, телесный угол луча антенны радиолокатора 0,01 стерадиан. Концентрация капель по результатам
экспериментальных исследований А. Беста при интенсивности дождя 5 мм\ч
составляет 3400![]() [18], действующая
поверхность антенны радиолокатора с площадью - 9 м2
[18], действующая
поверхность антенны радиолокатора с площадью - 9 м2
Импульсный объем при
локации слоя дождя: Vимп = =9·106 м3; для
малого диэлектрического шара эффективная поверхность рассеяния - So=300d2
=9·106 м3; для
малого диэлектрического шара эффективная поверхность рассеяния - So=300d2![]() = 2,4·10-8м2.
= 2,4·10-8м2.
S So = NVимп ; So » 21,6 м2.
При такой эффективной поверхности дождя объект с меньшим значением ЭПР может становится невидимым. Полоса более сильного дождя (диаметр капель 4- 5 мм) может создавать отраженные сигналы, намного превышающие отражения от тяжелого бомбардировщика.
1.2.4. Поляризационная матрица рассеяния модели объекта со статистическими неровностями поверхности
При определении энергетических и фазовых характеристик рассеяния отражателей со статистическими неровностями поверхности используются методы, разработанные для статистически шероховатых поверхностей естественного или антропогенного происхождения [18].
В дальнейшем будут использованы их основные результаты и положения, что необходимо для описания процесса моделирования элементов поляризационной матрицы рассеяния (ПМР). Перед рассмотрением упомянутых методик осуществляется выбор системы координат и определение электродинамики материала элементарного отражателя (ЭО).
Элементы ПМР определяются
в системе координат связанной с элементарным отражателем (собственный базис
ЭО), где ![]() и
и ![]() -
собственные базисы падающей и отраженной волн соответственно;
-
собственные базисы падающей и отраженной волн соответственно; ![]() - угол визирования падающей волны;
- угол визирования падающей волны; ![]() - углы места и азимута отраженной волны;
- углы места и азимута отраженной волны; ![]() - нормаль к поверхности ЭО в данной
точке.
- нормаль к поверхности ЭО в данной
точке.
Данная система координат является общей для всех методов и определяет условия облучения и наблюдения данного ЭО.
Параметрами базисов
падающей и отраженной волн являются перечисленные углы подхода в базисе ЭО: ![]() . Таким образом, инициализация базисов
. Таким образом, инициализация базисов ![]() как функций углов подхода осуществляется
следующим образом.
как функций углов подхода осуществляется
следующим образом.
Параметры облучения и
наблюдения ЭО ![]() используются во всех методах, а
положение нормали к поверхности ЭО определяется методикой, применяемой к
исследованию поверхности данного ЭО.
используются во всех методах, а
положение нормали к поверхности ЭО определяется методикой, применяемой к
исследованию поверхности данного ЭО.
Статистическими
параметрами шероховатой поверхности ЭО, используемыми в методах расчета ПМР
являются: ![]() - среднеквадратическое значение высоты
неровностей,
- среднеквадратическое значение высоты
неровностей, ![]() - интервал корреляции точек поверхности
ЭО,
- интервал корреляции точек поверхности
ЭО, ![]() - среднеквадратический угол наклона поверхности
ЭО.
- среднеквадратический угол наклона поверхности
ЭО.
Для гауссовой поверхности
с коэффициентом корреляции вида  среднеквадратический
угол наклона определяется как
среднеквадратический
угол наклона определяется как 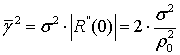 . В качестве оценочного
значения угла наклона примем
. В качестве оценочного
значения угла наклона примем 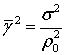 , умножая его на
соответствующий коэффициент, определяемый видом
, умножая его на
соответствующий коэффициент, определяемый видом ![]() ).
).
Рассматриваемые модели
применяются для статистически изотропных поверхностей, т. е. когда интервал
корреляции поверхности одинаков во всех направлениях ![]() .
.
Применение одной из
методик к анализу элементов ПМР ЭО определяется параметром Рэлея 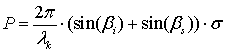 , в соответствии с которым, различают 3
вида неровностей поверхности ЭО: крупномасштабные (P>>1),
мелкомасштабные (P<<1) и двухкомпонентные (P~1). Для
каждого вида неровностей существуют следующие методики оценки элементов ПМР:
метод касательной плоскости, метод малых возмущений и метод двухкомпонентной
поверхности. Определение энергетических и фазовых характеристик с помощью
данных методов приведено в последовательности соответствующей их дальнейшему моделированию.
, в соответствии с которым, различают 3
вида неровностей поверхности ЭО: крупномасштабные (P>>1),
мелкомасштабные (P<<1) и двухкомпонентные (P~1). Для
каждого вида неровностей существуют следующие методики оценки элементов ПМР:
метод касательной плоскости, метод малых возмущений и метод двухкомпонентной
поверхности. Определение энергетических и фазовых характеристик с помощью
данных методов приведено в последовательности соответствующей их дальнейшему моделированию.
Таким образом, теоретически взаимодействие электромагнитных волн с проводящими объектами может быть описано путем комбинированного применения метода геометрической оптики для построения лучевых трубок и метода физической оптики для расчета поля рассеяния в дальней зоне.
2. АНАЛИЗ МЕТОДОВ ОБРАБОТКИ РАДИОЛОКАЦИОННЫХ СИГНАЛОВ
При рассмотрении вопросов обработки сигналов с помехами и оценке возможности снижения заметности наземных объектов, предполагается идеализация элементов приемника, которые будут использоваться при анализе и синтезе радиолокационных измерителей и систем обнаружения.
В классике, как правило, усилитель промежуточной частоты эквивалентен полосовому линейному фильтру, настроенному на промежуточную частоту [19]. При импульсном сигнале за счет применения стробирования в УПЧ возможна временная селекция. При этом временная селекция и фильтрация до детектирования являются существенной частью оптимальной обработки сигнала.
Второй детектор можно рассматривать как устройство, выделяющее огибающую входного случайного процесса (в случае линейного детектора) или квадрат огибающей (в случае квадратичного детектора).
Фазовый детектор при квадратичных характеристиках диодов эквивалентен простому устройству, перемножающему входные случайные процессы, с последующим выделением низкочастотных составляющих. Поэтому в дальнейшем операция перемножения сигналов означает необходимость пропускания сигналов через фазовый детектор такого вида.
Видеоусилители и усилители низкой частоты можно считать линейными безынерционными четырехполюсниками. Сведения по воздействию флюктуирующего сигнала на систему автоматического регулирования усиления (АРУ) в литературе хорошо известны и их в каждом конкретном случае применяются при соответствующем анализе приемных трактов конкретных РЛС.
При этом, как правило, относительно системы АРУ используются следующие идеализации:
- при линейном детекторе в регулируемом усилителе система АРУ изменяет среднее значение коэффициента усиления приемника обратно пропорционально величине математического ожидания огибающей случайного процесса на входе, так что среднее значение амплитуды напряжения на выходе остается примерно постоянным (нормирующее свойство АРУ);
- при квадратичном детекторе и системе АРУ с большой инерционностью поддерживается постоянным напряжение на выходе, равное произведению среднего коэффициента приемника на средний квадрат огибающей случайного процесса на входе;
- флюктуации в первом приближении отрабатываются системой АРУ как эквивалентной линейной системой с частотными характеристиками.
Далее будем считать, что указанные условия соблюдаются.
2.1. Современные методы обработки радиолокационных сигналов
Развитие математических методов (операций) и средств обработки сигналов информации радиотехнических систем, обеспечивающих успешное решение поставленных задач (наблюдения, распознавания радиоизображений, автосопровождения, наведения, а также передача информации) в условиях противодействия и обладающих высокой скрытностью функционирования представляется насущной проблемой. Решение этой проблемы осуществляется различными путями, приоритетными из которых в настоящее время могут быть следующие [20].
1. Совершенствование методов синтеза оптимальных и квазиоптимальных алгоритмов обнаружения полезного сигнала в радиолокационных системах (робастных алгоритмов), обладающих достаточно стабильными характеристиками при изменении условий работы, т.е. устойчивых при известных характеристиках полезного сигнала и помехи,
2. Разработка методов и способов анализа сигналов радиотехнических систем использующих сверхширокополосные сигналы, обеспечивающих решение приоритетных задач в радиолокации: точного измерения координат объекта с высокой вероятностью его распознавания (построение радиолокационных изображений).
3. Дальнейшее повышение технико-экономической эффективности цифровой обработки сигналов, основанной на синтезе достоинств программного и аппаратного подходов, как путем использования, заложенного в программно-алгоритмическом обеспечении высокого качества обработки, так и при реализации архитектуры вычислительных средств (аппаратное – в параметрах и архитектуре специализированных БИС).
4. Совершенствование поляризационных методов обработки радиолокационных сигналов, решение целого ряда приоритетных задач: согласования, подавления помех, распознавания радиолокационных объектов, разделения сигналов в системах с повторным использованием частот, практически во всех активных и пассивных радиотехнических системах:
в РЛС обнаружения и наведения миллиметрового диапазона волн;
в радиорелейных и спутниковых системах связи с повторным использованием частот на линиях тропосферной и коротковолновой связи для минимизизации поляризационных замираний;
во всех системах для повышения их эффективности использование динамического адаптивного подхода.
5. Дальнейшее развитие метода весовой обработки радиолокационных сигналов при дискретном преобразовании Фурье, относящегося к разновидности методов цифровой обработки и связанного с последними достижениями в этой области - синтезированием нового класса финитных функций теории аппроксимации, так называемых атомарных функций.
6. Разработка методов и способов обработки информации пассивных (радиометрических) систем обнаружения, распознавания неподвижных наземных укрытых и замаскированных объектов, в том числе и для «радиовидения» на небольших дальностях, а также для астрономических исследований и дистанционного зондирования земной поверхности.
7. Совершенствование фрактальных методов для обработки радиолокационных сигналов и изображений в сантиметровом и миллиметровом диапазонах радиоволн.
Ниже остановимся на последних интересных, на наш взгляд, методах обработки радиолокационных сигналов на фоне помех.
2.2. Оптимальное обнаружение сигналов в присутствии гармонических помех
В работе [21] определена структура инерционно-нелинейного преобразователя, входящего в приемник оптимального обнаружения сигналов на фоне коррелированных негауссовых помех. В качестве негауссовой помехи рассматривается стационарный случайный процесс, содержащий в своем составе квазидетерминированное гармоническое колебание. Получены энергетические характеристики оптимального приемника.
По мнению авторов, целесообразно также предположить, что при обосновании энергетических характеристик оптимального приемника и при условии, что в этом случае имеет место в поле излучения наличие квазидетерминированных гармонических колебаний (ГК), это может служить достаточно хорошей моделью паразитных излучений, создающих перекрестные помехи при приеме полезного сигнала.
Складываясь на входе приемника с гауссовским шумом (ГШ), такое колебание образует негауссовскую помеху, что позволяет решать поставленную задачу оптимального обнаружения сигналов в предположении, что гауссовский шум – белый.
Для определения структуры обнаружителя и исследования его качественных показателей при произвольной корреляции в аддитивном гауссовом шуме, воздействующем на приемник вместе с квазидетерминированным гармоническим колебанием, в работе приводится модель вероятностной характеристики помехи.
Предполагается, что на входе приемника действует негауссовская помеха
где ![]() -
квазидетерминированное ГК постоянной амплитуды А0, частоты ω0 и
случайной фазы, равномерно распределенной на интервале [0, 2π];
-
квазидетерминированное ГК постоянной амплитуды А0, частоты ω0 и
случайной фазы, равномерно распределенной на интервале [0, 2π]; ![]() - ГШ с нулевым средним значением
дисперсией и коэффициентом корреляции R(τ). Случайные процессы
- ГШ с нулевым средним значением
дисперсией и коэффициентом корреляции R(τ). Случайные процессы ![]() и
и ![]() будем считать стационарными и взаимно независимыми.
будем считать стационарными и взаимно независимыми.
Для определения требуемой
структуры приемника оптимального обнаружения сигналов на фоне помехи (2.1)
путем математического преобразования в работе [21] предложена математическая
модель (2.2) для системы случайных величин ![]()
![]() , определяющая двухмерную совместную плотность
вероятности процесса (3.1) при ω0= 0 (данный случай является
наихудшим с точки зрения подавления помехи нелинейными устройствами):
, определяющая двухмерную совместную плотность
вероятности процесса (3.1) при ω0= 0 (данный случай является
наихудшим с точки зрения подавления помехи нелинейными устройствами):
где ![]() -
функция, определяемая параметром а1 и аргументом
-
функция, определяемая параметром а1 и аргументом ![]() ,
которые равны:
,
которые равны: ![]()
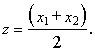
Выражение (2.2) позволяет сравнительно просто получить структуру приемника оптимального обнаружения и исследовать его эффективность в условиях действия коррелированной негауссовой помехи синусоидального типа.
Оптимальная обработка
выборочных значений ![]() принимаемого колебания
принимаемого колебания ![]() при обнаружении слабого
детерминированного сигнала
при обнаружении слабого
детерминированного сигнала ![]() на фоне негауссовой
помехи
на фоне негауссовой
помехи ![]() может быть представлен в виде [21]:
может быть представлен в виде [21]:
где n -
объем выборки; ![]()
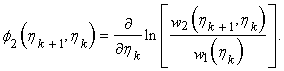 (2.4)
(2.4)
Обнаружитель (2.3) получен в предположении, что помеха (2.1) допускает представление в виде односвязной марковской модели и в предположении слабого сигнала, при котором отношение сигнал-помеха на входе приемника много меньше единицы. Подставляя (2.2) в (2.3), (2.4), получим
Функция ![]() в (2.6), (2.7) определяется с помощью
переменных, соответствующих (2.3).
в (2.6), (2.7) определяется с помощью
переменных, соответствующих (2.3).
Первое слагаемое в (2.5)
является результатом нелинейной обработки в безынерционном нелинейном
преобразователе НП1 с характеристикой (2.6) полусуммы ![]() выборочных значений принимаемого
колебания с последующей фильтрацией в фильтре, согласованном с полусуммой
выборочных значений принимаемого
колебания с последующей фильтрацией в фильтре, согласованном с полусуммой ![]() значений сигнала. Второе слагаемое в (2.5)
соответствует безынерционному НП2 с характеристикой (2.7) выборочных
значений принимаемого колебания с последующей фильтрацией в фильтре,
согласованном с сигналом (
значений сигнала. Второе слагаемое в (2.5)
соответствует безынерционному НП2 с характеристикой (2.7) выборочных
значений принимаемого колебания с последующей фильтрацией в фильтре,
согласованном с сигналом (![]() ). Третье слагаемое в (2.5)
является результатом обработки по схеме последовательного соединения
режекторного и согласованного фильтров. Схема обнаружителя, соответствующая (2.5),
приведена на рис. 2.1, где ∆t - устройство задержки; «+», «-» - формирователи полусуммы и полуразности
значений принимаемого колебания; НП1, НП2 - нелинейные преобразователи с
характеристиками (2.6), (2.7), соответственно;
). Третье слагаемое в (2.5)
является результатом обработки по схеме последовательного соединения
режекторного и согласованного фильтров. Схема обнаружителя, соответствующая (2.5),
приведена на рис. 2.1, где ∆t - устройство задержки; «+», «-» - формирователи полусуммы и полуразности
значений принимаемого колебания; НП1, НП2 - нелинейные преобразователи с
характеристиками (2.6), (2.7), соответственно; ![]() -
усилитель с коэффициентом усиления 4α/(1 - R); ПУ - пороговое устройство.
-
усилитель с коэффициентом усиления 4α/(1 - R); ПУ - пороговое устройство.
Следует отметить, что оба НП в схеме на рис. 2.1 являются безынерционными и имеют характеристики преобразования, определяемые одномерным распределением помехи при соответствующих значениях переменных. Канал обработки с НП2 вида (2.7) соответствует обнаружителю сигнала на фоне негауссовой помехи (2.1) с независимыми выборочными значениями [21]. При этом продукт преобразования этого канала входит в (2.5) с отрицательным знаком.
Таким образом, оптимальный алгоритм (2.5) обнаружения детерминированного сигнала как при малых, так и при больших значениях параметра а сводится к обработке по гауссовым алгоритмам, которые рассмотрены в [21] и соответствуют коррелированной гауссовой помехе. Во всех других случаях оптимальный обнаружитель (2.5) представляется инерционно-нелинейным преобразователем (ИНП) (рис.2.1), включающим в себя инерционное звено (блок задержки) и безынерционные нелинейные звенья с характеристиками (2.6), (2.7), определяемыми одномерным распределением помехи.
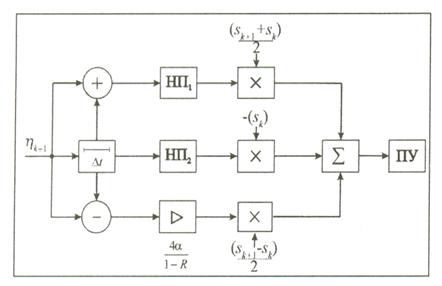
Рис. 2.1. Схема обнаружителя.
Качество оптимальной обработки (2.5) можно определить коэффициентом подавления μopt коррелированной негауссовской помехи (2.1), характеризующим меру изменения отношения сигнал-помеха за счет включения ИНП в тракт приемника: μopt = qИНП / q вх , где qИНП - отношение сигнал-помеха на выходе НПП; q вх - отношение сигнал-помеха на входе ИНП.
При условиях, сформулированных в [21], величина коэффициента подавления μopt может быть найдена как
![]() (2.8)
(2.8)
где ![]() -
мощность помехи на входе приемника;
-
мощность помехи на входе приемника; ![]() - усреднение по совокупности;
- усреднение по совокупности;
![]() - функции, определяемые с помощью (2.4);
величина
- функции, определяемые с помощью (2.4);
величина ![]() является характеристикой формы сигнала
[20].
является характеристикой формы сигнала
[20].
Подставляя (2.4) в (2.8), производя усреднение с помощью (2.2), получаем
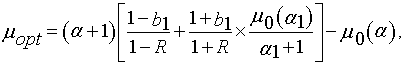 (2.9)
(2.9)
где через ![]() обозначена функция
вида
обозначена функция
вида
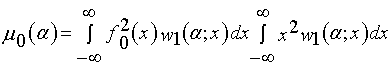 , (2.10)
, (2.10)
определяющая собой качество
оптимальной обработки на фоне негауссовой помехи (2.1) с независимыми
выборочными значениями [21]. При этом характеристика ![]() в
(2.9) соответствует функции (2.10) при значении аргумента
в
(2.9) соответствует функции (2.10) при значении аргумента ![]() .
.
Для случая малых и
больших значений а величину коэффициента подавления (2.9) и принимая во
внимание, что при а = 0 величина ![]() из (2.10)
равна единице, то (2.9) можно получить
из (2.10)
равна единице, то (2.9) можно получить
![]() (2.11)
(2.11)
Величина коэффициента подавления (2.11) является характеристикой эффективности обнаружителя. Она характеризует качество оптимального приемника, работающего в условиях коррелированных гауссовых помех.
Графики отношения![]() в функции от R, вычисленного с помощью (2.9), (2.11) для а =
50 и для разных значений а, приведены на рис. 2.2. Как следует из этих
кривых, эффективность оптимального обнаружителя (2.5) значительно превышает
эффективность гауссовского приемника и существенно зависит от коэффициента
корреляции аддитивного гауссовского шума n(t)
в (2.1).
в функции от R, вычисленного с помощью (2.9), (2.11) для а =
50 и для разных значений а, приведены на рис. 2.2. Как следует из этих
кривых, эффективность оптимального обнаружителя (2.5) значительно превышает
эффективность гауссовского приемника и существенно зависит от коэффициента
корреляции аддитивного гауссовского шума n(t)
в (2.1).
Таким образом, в работе [21] на основании двухмерного дифференциального закона распределения вероятностей коррелированной негауссовской помехи (2.1) определена структура ИНП, входящего в приемник оптимального обнаружения.
Найдены и исследованы алгоритмы оптимального обнаружения, соответствующие малым и большим значениям отношения сигнал-помеха. Показано, что в предельных случаях оптимальная обработка может быть построена по алгоритмам, соответствующим коррелированному гауссовоскому шуму.
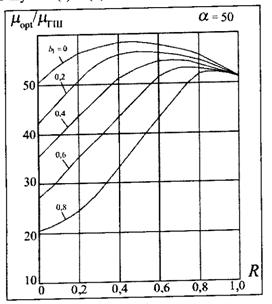
Рис. 2.2. Графики зависимости
величины отношения ![]() в функции от R при а = 50 и различных значениях
в функции от R при а = 50 и различных значениях ![]() .
.
Рассмотрена эффективность оптимальной обработки. Показано что приемник оптимального обнаружения сигналов в условиях воздействия коррелированной негауссовой помехи (2.1) обладает значительным энергетическим преимуществом по сравнению с гауссовым приемником. Эффективность оптимального обнаружителя также существенно выше эффективности приемника, работающего в условиях негауссовой помехи с независимыми выборочными значениями.
Полученные результаты могут быть использованы для построения обнаружителей сигналов, работающих в условиях коррелированных негауссовых помех.
2.3. Метод анализа при обработке сигнала с учетом связи между стохастической матрицей и параметрами, характеризующими обработку сигнала
Для определения стохастической матрицы необходимо определить элементы матрицы с учетом физических характеристик. В наиболее сложном варианте при оценке параметров сигнала радиолокационного канала (РК), алгоритм которого может быть описан следующим образом [22]:
1. На входе блока
действует сигнал с параметром ![]() .
.
2. В блоке этот сигнал взаимодействует с помехой.
3. Сигнал обрабатывается
оптимальным методом, удовлетворяющим критерию минимума, среднего риска, в
результате чего выдается оценка параметра ![]() .
.
4. Оценка параметра
производится с ошибкой ![]()
где - ![]() истинное
значение параметра, соответствующее безошибочному преобразованию
истинное
значение параметра, соответствующее безошибочному преобразованию ![]() . Ошибка
. Ошибка ![]() подчиняются
нормальному закону распределения.
подчиняются
нормальному закону распределения.
5. Измеренное значение ![]() подается на квантующее устройство.
Последнее относит его к тому значению параметра
подается на квантующее устройство.
Последнее относит его к тому значению параметра ![]() , в
область которого попала величина
, в
область которого попала величина ![]() . При этом в общем
случае справедливо неравенство
. При этом в общем
случае справедливо неравенство ![]() .
.
6. При квантовании используются правила решения:
а) ![]() , если
, если ![]() при
j = 2 · · · (m-1);
при
j = 2 · · · (m-1);
б) ![]() , если
, если ![]() ;
;
в) ![]() , если
, если ![]() .
.
Предположим, что при
подаче на вход блока сигнала с параметром ![]() , на
выходе его устройства оптимальной обработки получим сигнал, оценка параметра
, на
выходе его устройства оптимальной обработки получим сигнал, оценка параметра ![]() которого будет распределена по закону
которого будет распределена по закону
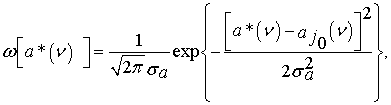 (2.12)
(2.12)
где предполагается, что математическое ожидание параметра на входе устройства обработки равно
![]()
Подобное предположение означает, что в рассматриваемом блоке устранены систематические ошибки.
Элементы стохастической
матрицы блока можно определять как вероятность того, что оценка ![]() параметра сигнала попадает в пределы
некоторой градации j
. Так, при условии перехода по схеме i → j o (рис.2.3)
компоненты матрицы Z(ν):
параметра сигнала попадает в пределы
некоторой градации j
. Так, при условии перехода по схеме i → j o (рис.2.3)
компоненты матрицы Z(ν):
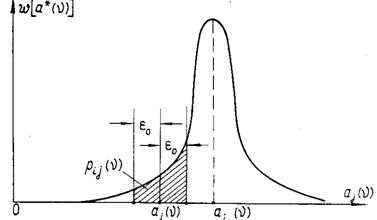
Рис. 2.3. Компоненты матрицы Z(ν).
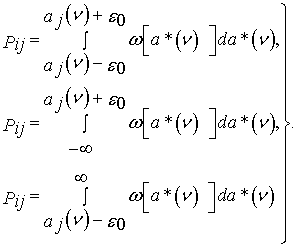 (2.13)
(2.13)
В полученной формуле при j 0 = 1 нижний предел![]() = -∞, а при j 0 = m верхний предел
= -∞, а при j 0 = m верхний предел ![]() .
.
При вводе вспомогательной величины
![]() ,
(2.15)
,
(2.15)
которая равна разности номера j рассматриваемой градации и номера
градации ![]() , соответствующей безошибочному
преобразованию сигнала блоком по правилу
, соответствующей безошибочному
преобразованию сигнала блоком по правилу ![]() Тогда,
принимая во внимание исходное условие
Тогда,
принимая во внимание исходное условие ![]() ,
аргументы интегралов вероятностей в формуле (2.14) запишем в виде
,
аргументы интегралов вероятностей в формуле (2.14) запишем в виде
 (2.16)
(2.16)
 (2.17)
(2.17)
![]() где отношение
где отношение 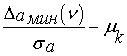 -
коэффициент достоверности по параметру сигнала
-
коэффициент достоверности по параметру сигнала ![]() .
.
С учетом этого обстоятельства и формул (2.16), (2.17) выражение (2.14) для переходных вероятностей стохастической матрицы приводится к виду
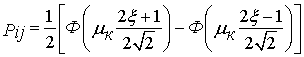 .
(2.18)
.
(2.18)
Таким образом, получена формула для вычисления элементов стохастической матрицы блока, в котором оценка параметра радиолокационного сигнала производится с ошибкой, подчиняющейся нормальному закону распределения. Формула (2.18) учитывает уровень помех, действующих в канале, и особенности обработки отраженного сигнала.
В качестве примера в [22] с помощью полученных соотношений были рассчитаны элементы стохастической матрицы блока при следующих условиях:
1) на выходе блока воспроизводится 9
градаций параметра ![]() ;
;
2) преобразование ![]() происходит по схеме
происходит по схеме ![]() ;
;
З) величина градации (шаг квантования)
параметра ![]() выбрана так, что
выбрана так, что ![]() .
.
Результаты проведенных вычислений представлены матрицей в табл.2.I.
Рассмотрение стохастической матрицы (табл.2,I) показывает, что она близка к симметричной. Отклонения от симметрии имеют место в первом и последнем столбцах матрицы.
Таблица 2.1. Стохастическая матрица блока
|
i / j* |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
0,6915 |
0,242 |
0,061 |
0,00525 |
0,00025 |
5·10 -6 |
5·10 -8 |
5·10 -11 |
0 |
|
2 |
0,3085 |
0,383 |
0,242 |
0,061 |
0,00525 |
0,00025 |
5·10 -6 |
5·10 -8 |
5·10 -11 |
|
3 |
0,0665 |
0,242 |
0,383 |
0,242 |
0,061 |
0,00525 |
0,00025 |
5·10 -6 |
5·10 -8 |
|
4 |
0,0055 |
0,061 |
0,242 |
0,383 |
0,242 |
0,061 |
0,00525 |
0,00025 |
5·10 -6 |
|
5 |
0,00025 |
0,00525 |
0,061 |
0,242 |
0,383 |
0,242 |
0,061 |
0,00525 |
0,00025 |
|
6 |
5·10 -6 |
0,00025 |
0,00525 |
0,061 |
0,242 |
0,383 |
0,242 |
0,061 |
0,00525 |
|
7 |
5·10 -8 |
5·10 -6 |
0,00025 |
0,00525 |
0,061 |
0,242 |
0,383 |
0,242 |
0,065 |
|
8 |
5·10 -11 |
5·10 -8 |
5·10 -6 |
0,00025 |
0,00525 |
0,061 |
0,242 |
0,383 |
0,3085 |
|
9 |
0 |
5·10 -11 |
5·10 -8 |
5·10 -6 |
0,00025 |
0,00525 |
0,061 |
0,242 |
0,6915 |
Примечание: *)
i - значения по вертикали; j – значения по горизонтали.
Эти отклонения
обусловлены особенностями принятия решения на краях диапазона возможных
значений ![]() . В остальных столбцах элементы симметричны
относительно диагонали матрицы. Это обстоятельство является следствием
принятого предположения о нормальном законе распределения ошибок измерений и
неизменности значения дисперсии ошибок
. В остальных столбцах элементы симметричны
относительно диагонали матрицы. Это обстоятельство является следствием
принятого предположения о нормальном законе распределения ошибок измерений и
неизменности значения дисперсии ошибок ![]() для
всех преобразований
для
всех преобразований ![]() , производимым данным блоком.
, производимым данным блоком.
ЗАКЛЮЧЕНИЕ
1. Исследования резонансов поглощения дециметровых, сантиметровых и миллиметровых в атмосферных газах для повышения помехозащищенности РЛС при обнаружении объектов необходимо проводить на частотных резонансах как с максимальными, так и минимальным поглощением. Это позволит оценить особенности взаимодействия электромагнитных волн с проводящими объектами в различных диапазонах волн и осуществить оптимальный выбор рабочей частоты с учетом требований , налагаемых на функционирование РЛС в условиях помеховой обстановки.
2. Результаты проведенного анализа могут быть использованы в исследованиях по оценке эффективности помехозащищенности РЛС при радиоэлектронном противодействии, а также для выработки практических рекомендаций по основным параметрам РЛС и их техническому облику.
3. Проведенный анализ методов обработки радиолокационных сигналов при обнаружении наземных объектов, позволивший определить пути решения этой проблемы, приоритетными из которых могут быть следующие:
- совершенствование методов синтеза оптимальных и квазиоптимальных алгоритмов обнаружения полезного сигнала в радиолокационных системах (робастных алгоритмов), обладающих достаточно стабильными характеристиками при изменении условий работы, т.е. устойчивых при известных характеристиках полезного сигнала и помехи;
- разработка методов и способов анализа сигналов радиотехнических систем использующих сверхширокополосные сигналы, способных обеспечить решение приоритетных задач в радиолокации: точного измерения координат объекта и с высокой вероятностью его распознавания (построение радиолокационных изображений);
- дальнейшее повышение технико-экономической эффективности цифровой обработки сигналов, основанной на синтезе достоинств программного и аппаратного подходов, как путем использования, заложенного в программно-алгоритмическом обеспечении высокого качества обработки, так и при реализации архитектуры вычислительных средств (аппаратное – в параметрах и архитектуре специализированных БИС).
Литература
1. Борзов А.Б., Соколов А.В., Сучков В.Б. Методы цифрового моделирования радиолокационных характеристик сложных объектов на фоне природных и антропогенных образований. // Вопросы перспективной радиолокации. Коллективная монография. /под ред. А.В. Соколова. – М.: Радиотехника, 2003. - с. 279-302.
2. Antifeev V.N., Borsov A.B., Bystrov R.P., Nosdrachev D.A., Pavlov G.L., Sokolov A.V. Digital Computer Simulation of Radar scattering Fields for Complex Shape Objects. // Proc.MWS Kharkov 1998. -p.494-495.
3. Быстров Р.П., Загорин Г.К., Соколов А.В., Федорова Л.В. Пассивная радиолокация: методы обнаружения объектов (монография). // Изд. «Радиотехника», 2008. – 300 с.
4. Бункин Б.В, Реутов А.П.. Направления развития радиолокационных систем.// Наукоемкие технологии, № 4-2002, - с. 8-12.
5. Быстров Р.П., Потапов А.А., Соколов А.В. Миллиметровая радиолокация с фрактальной обработкой. // М.Радиотехника. 2005 г. – с. 367.
6. Шустов Э.И. Радиолокационное обнаружение малозаметных целей. //Вопросы перспективной радиолокации. Коллективная монография. Под ред. А.В. Соколова. М.: Радиотехника, 2003. – с. 178-187.;
7. Акимов В.Ф., Евстратов Ф.Ф. результаты исследований влияния ионосферных и помеховых условий на работу коротковолновых загоризонтных локаторов. //Вопросы перспективной радиолокации. Коллективная монография. Под ред. А.В. Соколова. М.: Радиотехника, 2003. –с.333-357.
8. Jane's Def. Weekly. -1997. - 27, №24.—С.6.
9. Cook Nick, Starr Barbara and oth. // Jane's Def. Weekly/ - 1997. - 27, №23. -С. 47, 49, 51, 53-54, 57-58, 60, 62, 64, 66.
10. Norris Guy / Flight Int. - 1997/ - 151, №4577. - С. 17.
11. Jane's Def. Weekly. - 1997. - 27, №10. -С. 94.
12. Geile H.J. / Schiff und Hafen: Seewirt., Kommandobruke [Schiff und Hafen Seewirt.]. - 1997. - 49, №9.—С. 88-91.
13. Wardrop B. / GEC J. Technol. [GEC J. Res.]. – 1997. – 14, № 3. – С. 141-149.
14. Неубивающее оружие воздействия на большие скопления людей. ADS is a don't kill 'em cook'em crowd control weapon. / Neale Ron. // Electron. Eng. 2001. 73, № 892, c. 39, 40; РЖ 24В. Радиолокация, № 11, 2001 г.
15. Борзов А.Б., Соколов А.В., Сучков В.Б.. Результаты цифрового моделирования характеристик рассеяния объектов сложной электрофизической структуры и формы. //Вопросы перспективной радиолокации. Коллективная монография. Под ред. А.В. Соколова. М.: Радиотехника, 2003. –с. 256-272.
16. Богомолов А.Ф. Основы радиолокации. // М.: Сов. радио, 1954. – 303 с.
17. Соколов А.В. Распространение миллиметровых и субмиллиметровых радиоволн в атмосфере Земли. // Итоги науки и техники. Радиотехника, т.5, М . 1974. ВИНИТИ. – с. 5-109.
18. Акиншин Н.С., Румянцев В.Л., Процюк С.В. Поляризационная селекция и распознавание радиолокационных сигналов. – Тула.: Лидар, 2000. – 316 с.
19. Бакут П.А., Большаков И.А., Тартаковский Г.П. и др. Вопросы статистической теории радиолокации. Том 1. Под общ. ред. Г.П. Тартаковского. – М: Сов. Радио, 1963. – 421 с.
20. Вопросы перспективной радиолокации. Коллективная монография. / Под ред. А.В. Соколова. – М.: Радиотехника, 2003. – 512 с.
21. Данилов ВА., Жабинский Ю.В. Оптимальное обнаружение сигналов в присутствии гармонических помех. – М.:, “Радиотехника”, 2006 г., № 1
22. Борзов А.Б., Быстров Р.П., Засовин Э А., Илясов Е.П., Потапов А.А., Соколов А.В., Титов А.Н. Радиотехнические и радиооптические системы./ Под ред. Э.А. Засовина. –М.: Изд-во «Круглый стол», 2001. – 752 с.