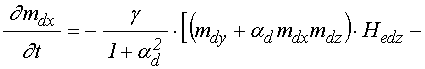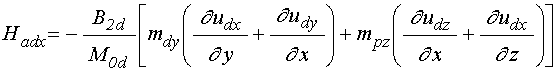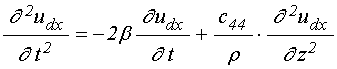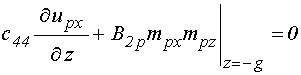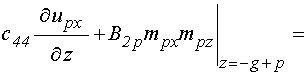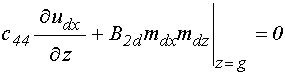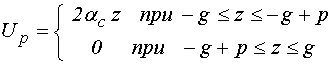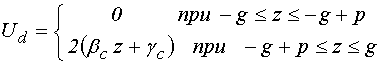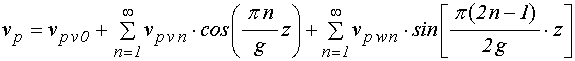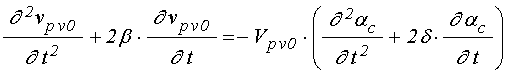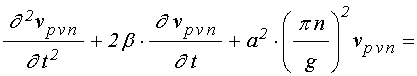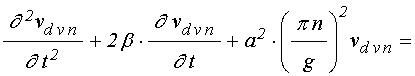Влияние подложки на магнитоупругие колебания в структуре "магнитная пленка

УДК 537.874; 537.624

ВЛИЯНИЕ ПОДЛОЖКИ НА МАГНИТОУПРУГИЕ КОЛЕБАНИЯ В СТРУКТУРЕ «МАГНИТНАЯ ПЛЕНКА – НЕМАГНИТНАЯ ПОДЛОЖКА»

П. М. Ветошко, В. Г. Шавров, В. И. Щеглов
Институт радиотехники и электроники им. В.А.Котельникова РАН

Статья получена 2 августа 2015 г.

Аннотация. Рассмотрено возбуждение магнитоупругих колебаний в структуре «магнитная пленка – немагнитная подложка» на примере схем магнитострикционного преобразователя и ротационного магнетометра. Показано, что вклад диссипации упругой системы в диссипацию магнитной системы незначителен, то есть диссипация магнитной системы определяется внутренними процессами магнитной релаксации в пленке. Пленка колеблется так, как если бы на границе с подложкой имела жесткое закрепление. Амплитуда колебаний подложки значительно меньше амплитуды колебаний пленки. Указано на существование квазистатической сдвиговой деформации подложки, определяемой свойствами возбуждения и симметрии магнитного поля.

Ключевые слова: структура «пленка-подложка», магнитоупругое взаимодействие, магнитострикционный преобразователь, ротационный магнитометр.

Abstract. The excitation of magnetoelastic vibrations in structure “magnetic film – nonmagnetic foundation” on examples of magnetostriction transducer and rotational magnetometer schemes is considered. It is shown that the contribution of elastic system dissipation into magnetic system dissipation is very small, so as the dissipation of magnetic system is defined by intrinsic processes of magnetic relaxation in the film. The film vibrates are so as its may have on the boundary of foundation the hard fixation. The vibration amplitude of foundation is much smaller than the vibration amplitude of film. It is shown that there is quasi-static shift deformation of foundation which is determined by properties of excitation and symmetry of magnetic field.

Key words: structure “film – foundation”, magnetoelastic interaction, magnetostriction transducer, rotational magnetometer.

Введение

Пленки ферритов, в первую очередь железоиттриевого граната (ЖИГ), находят широкое применение в технике СВЧ [1-3]. Важной областью таких применений является возбуждение мощного гиперзвука с помощью магнитострикционного преобразователя [4-7]. Еще одно применение находят пленки ЖИГ в качестве чувствительного элемента ротационного магнитометра, предназначенного для измерения сверхслабых магнитных полей [8-15].

В обоих этих случаях пленки представляют собой тонкие слои, выращенные на относительно толстых подложках. При этом толщина пленки составляет обычно , а толщина подложки – , то есть на один-два порядка больше. Пленки ЖИГ обладают ярко выраженными магнитоупругими свойствами [6], так что колебания намагниченности в пленке неизбежно вызывают интенсивные колебания упругого смещения как в самой магнитной пленке, так и в немагнитной подложке.

В качестве подложки обычно используется гадолиний-галлиевый гранат (ГГГ), упругие параметры которого близки к таковым для ЖИГ, тогда как магнитные свойства полностью отсутствуют.

Обязательным требованием во всех перечисленных применениях является отсутствие помех от параметрического возбуждения обменных спиновых волн, не позволяющих превысить углы раскрыва прецессии намагниченности больше одного-двух градусов [16,17]. Удачным средством против такой помехи является выбор геометрии рабочего элемента устройства в виде пленки, намагниченной по нормали к ее плоскости [18-23]. Такая геометрия позволяет успешно достичь углов прецессии в десятки градусов, что дает возможность работы на высоких уровнях мощности а сильно нелинейном режиме [7].

В работах [24,25] рассмотрено возбуждение гиперзвука в двухслойной структуре, оба слоя которой обладают магнитными свойствами. Показано, что двухслойная структура в условиях ферромагнитного резонанса (ФМР) позволяет повысить мощность возбуждаемого гиперзвука более чем в два раза и расширить полосу частот также вдвое по сравнению с однослойной. При этом толщины обоих слоев структуры имеют одинаковый порядок, а суммарная толщина структуры в целом подбирается такой, чтобы удовлетворить условиям резонансного возбуждения первой упругой моды на частоте ФМР.

Однако в большинстве реальных применений подложка является немагнитной, а частота упругого резонанса структуры в целом оказывается более чем на порядок ниже частоты ФМР.

В работах [14,15] рассмотрена роль упругих свойств магнитоупругой пленки в схеме ротационного магнитометра. Показано, что в условиях близости между частотами ФМР и упругого резонанса чувствительность магнитометра ограничивается диссипацией колебаний в упругой системе, то есть затухание колебаний магнитной системы формируется в значительной степени за счет диссипативных свойств системы упругой.

Однако при этом учтена роль диссипативных свойств только самой пленки без подложки, что нельзя считать достаточно полным. Кроме того, следует отметить, что ротационный магнитометр обычно работает на частотах не более единиц МГц, то есть значительно ниже частоты ФМР, так что резонансные условия для пленки ЖИГ далеко не выполняются.

Из проведенного рассмотрения можно видеть, что как при возбуждении мощного гиперзвука при ФМР, так и при измерении слабых магнитных полей с помощью ротационного магнитометра вдали от частоты ФМР, в обоих случаях важную роль наряду с самой магнитной пленкой играет жестко с ней связанная достаточно толстая немагнитная подложка. Рассмотрению роли такой подложки и посвящена настоящая работа.

1. Общая геометрия задачи

В основу дальнейшего рассмотрения будет положена двухслойная структура типа «магнитная пленка – немагнитная подложка». Главное различие между постановкой задач о магнитострикционном преобразователе и ротационном магнитометре будут состоять в способе возбуждения колебаний намагниченности, геометрии подачи постоянного и переменного полей, а также в частоте переменного поля. Некоторое конструктивное отличие состоит в форме плоскостных элементов структуры. Кроме того, в этих двух задачах используются несколько отличные обозначения. Поэтому рассмотрим геометрию обеих задач в отдельности несколько более подробно.

2. Геометрия магнитострикционного преобразователя

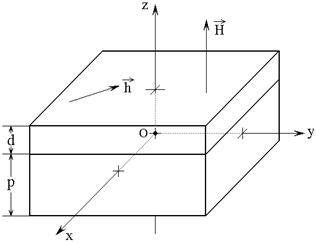
Общая геометрия задачи о магнитострикционном преобразователе, аналогичная принятой в работах [24,25], показана на рис.1.

Рис.1. Общая геометрия задачи о магнитострикционном преобразователе.

Основу преобразователя составляет двухслойная структура из двух жестко соединенных вместе бесконечно протяженных пластин – пленки и подложки. Толщина магнитной пленки равна , толщина подложки – , полная толщина структуры: . Начало координат декартовой системы выбрано на середине толщины структуры в целом. Упругие свойства пленки и подложки одинаковы. Пленка имеет магнитные и магнитоупругие свойства, подложка таковых не имеет. Пленка и подложка имеют кубическую кристаллографическую анизотропию с ориентацией оси (100) вдоль координатной оси .

Внешнее постоянное магнитное поле приложено перпендикулярно плоскости пленки. В плоскости пленки действует переменное магнитное поле

, (1)

имеющее круговую поляризацию с частотой , так что:

, . (2)

Упругие колебания возбуждаются в пленке под действием поля за счет магнитострикции. Возбуждаемая упругая волна имеет поперечную поляризацию и распространяется перпендикулярно плоскости пленки – вдоль оси .

3. Геометрия ротационного магнетометра

Общая геометрия задачи о ротационном магнетометре, с точностью до обозначений аналогичная принятой в работах [14,15], показана на рис.2.

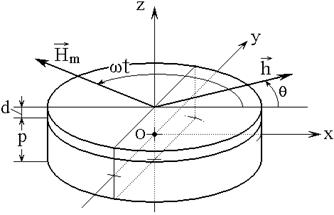
Рис.2. Общая геометрия задачи о ротационном магнетометре.

Основу магнетометра составляет пленка железоиттриевого граната (ЖИГ) толщиной на подложке толщиной . Полная толщина структуры также равна . Магнитные и упругие свойства пленки и подложки аналогичны предыдущему случаю (раздел №2).

Декартова система координат ориентирована таким образом, что плоскость совпадает с плоскостью пленки, а ось этой плоскости перпендикулярна. Начало координат выбрано на середине толщины структуры в целом. Упругие свойства пленки и подложки одинаковы. Пленка имеет магнитные и магнитоупругие свойства, подложка таковых не имеет. Пленка и подложка имеют кубическую кристаллографическую анизотропию с ориентацией оси (100) вдоль координатной оси .

Внешнее постоянное поле отсутствует:. В плоскости пленки приложено поле

, (3)

вращающееся с частотой . Его компоненты имеют вид:

, . (4)

Измеряемое поле неизменно во времени и приложено также в плоскости пленки под углом к оси , то есть:

. (5)

Измерение поля осуществляется с помощью катушки (на рис.2 не показана), надетой на пленку таким образом, что плоскость ее витков параллельна плоскости . Измерение состоит в регистрации сигнала двойной частоты , снимаемого с измерительной катушки, который наводится в ней вращающимся вектором намагниченности.

4. Особенности математического аппарата для структуры «пленка-подложка»

При расчете будем использовать математический аппарат, первоначально развитый для одного слоя в работе [26] и усовершенствованный затем в работах [27-30]. В основном будем следовать расширенному варианту такого аппарата, примененному к случаю двухслойной магнитоупругой структуры в работах [24,25]. Чтобы не нарушать общую идеологию аналитических вычислений, на начальном этапе будем полагать, что оба слоя, то есть как пленка, так и подложка наравне обладают магнитными, упругими и магнитоупругими свойствами. После того как основное решение будет получено, обратимся к требованиям настоящей задачи, для чего намагниченность и константу магнитоупругости подложки положим достаточно малыми.

Замечание. Положить намагниченность подложки сразу равной нулю нельзя, так как на нее осуществляется нормировка, в результате чего возникает неопределенность типа «нуль деленный на нуль». Чтобы при этом максимально приблизиться к реальности, в рамках настоящей работы будем полагать намагниченность подложки на пять порядков меньше намагниченности пленки. Опыт показывает, что дальнейшее уменьшение намагниченности подложки конечных результатов не меняет (с точностью до тысячных долей процента), то есть для практических целей вполне приемлемо. На константу магнитоупругости каких-либо ограничений нет, поэтому ее сразу можно положить равной нулю.

5. Плотность энергии структуры

Плотность энергии структуры в поле (где , для обеих задач имеют соответствующие значения (1)-(2) или (3)-(4)) равна сумме плотностей магнитной, упругой и магнитоупругой энергий слоев. С учетом членов, важных для дальнейшего рассмотрения, она имеет вид:

, (6)

где: – вектор намагниченности пленки, нормированный на ее намагниченность насыщения ; – компоненты тензора деформаций пленки и подложки (), соответствующие упругим смещениям ; – константа магнитоупругого взаимодействия в пленке (в [6] обозначенная как); – константы упругости (для обоих слоев одинаковые), – подобное же выражение с заменой индекса на .

6. Основные уравнения и граничные условия

Плотность энергии (6) позволяет записать полные уравнения движения для векторов намагниченности и упругих смещений для каждого из слоев, а также граничные условия, состоящие в отсутствии упругих напряжений на внешних поверхностях структуры в целом в совокупности с равенством напряжений и смещений на границе раздела слоев.

Аналогично [24,25], будем полагать распределение намагниченностей и внутри обоих слоев однородным.

Уравнения движения для компонент намагниченности в слое имеют вид:

; (7)

а уравнения для и получаются отсюда циклической перестановкой , , . Здесь – константа затухания для намагниченности, – гиромагнитная постоянная, а эффективные поля равны:

; (8)

; (9)

; (10)

где:

, (11)

а и получаются циклической перестановкой , , . Уравнения движения для намагниченности в слое аналогичны приведенным со взаимной заменой индексов и .

Относительно упругих смещений, аналогично [24,25], примем следующие предположения:

упругие смещения, перпендикулярные плоскости структуры, отсутствуют, то есть ;

упругие смещения в плоскости структуры и являются однородными, то есть .

Уравнение движения для - компоненты упругого смещения в слое имеет вид:

; (12)

где – параметр упругого затухания, – плотность материала, для обоих слоев одинаковая. Уравнение движения для - компоненты упругого смещения в том же слое получается из (12) путем замены индекса на , а уравнение движения для - компоненты в силу принятых предположений отсутствует. Уравнения движения для тех же компонент упругих смещений в слое аналогичны (12) с заменой индекса на .

Граничные условия для намагниченности в силу ее однородности не нужны, а граничные условия для - компонент смещений в слоях и имеют вид:

на нижней поверхности структуры, при :

; (13)

на границе между слоями, при :

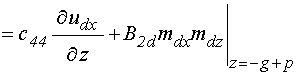; (14)

; (15)

на верхней поверхности структуры, при :

. (16)

Граничные условия для - компонент смещений в тех же слоях имеют вид, аналогичный (13)-(16), с заменой индекса на .

Таким образом, полная система содержит: для компонент намагниченности шесть уравнений первого порядка без граничных условий, а для компонент упругих смещений – четыре уравнения второго порядка и восемь граничных условий.

Уравнения колебаний намагниченности и упругого смещения в каждом из слоев взаимно независимы, а связь между ними осуществляется только через граничные условия (13)-(16). Это позволяет рассматривать задачу в целом, как граничную задачу для упругости, где намагниченности слоев играют роль параметров. Благодаря независимости задач для и компонент упругого смещения друг от друга, далее будет достаточно рассмотреть задачу только для - компоненты.

7. Разделение задачи для упругости на сумму двух задач

Совокупность выражений (12)-(16) – задача для функций и двух переменных и , для которых имеются уравнения второго порядка, содержащие производные по обеим переменным, но не содержащие самих функций (то есть однородные), дополненные граничными условиями для тех же функций и их первых производных по одной из переменных – , содержащими в качестве параметров функции другой переменной – (то есть неоднородными).

Для решения такой задачи, аналогично случаю одного слоя [26], следуя [24,25], воспользуемся классическим приемом разделения зависимости полного решения от координаты на две части – линейную и нелинейную [31]. Так, положим:

; (17)

, (18)

где и будем полагать линейными функциями координаты при ненулевых граничных условиях, а и – нелинейными функциями той же координаты при нулевых граничных условиях.

Таким образом, исходная задача разбивается на две задачи – первая для функций и , вторая – для функций и , полное же решение является суммой решений этих двух задач.

8. Решение первой задачи

Согласно [24,25], решение первой задачи (с точностью до обозначений) имеет вид:

; (19)

, (20)

где:

; (21)

; (22)

. (23)

9. Решение второй задачи

Решение второй задачи ищется в виде разложения в ряд Фурье по собственным функциям задачи с нулевыми граничными условиями:

;(24)

; (25)

где , , – зависящие только от времени функции, являющиеся решениями уравнений:

для слоя :

; (26)

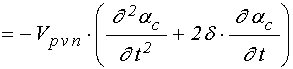; (27)

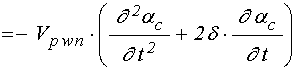; (28)

для слоя :

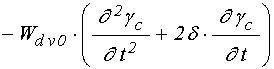; (29)

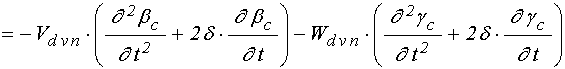; (30)

. (31)

где коэффициенты , , представляют собой линейные комбинации из тригонометрических функций, явный вид которых приведен в работах [24,25] и здесь опущен ввиду громоздкости.

10. Решение полной задачи для упругости

Таким образом, решение полной задачи для упругости (12)-(16) принимает вид:

; (32)

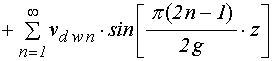. (33)

Полученные формулы содержат зависимость от координаты , что позволяет найти упругие смещения в любой точке слоев или соответственно. Чтобы найти смещения на внешних поверхностях структуры, надо в формуле (32) положить , а в формуле (33) положить .

Напомним, что приведенные здесь выражения получены для - компоненты упругого смещения. Для получения - компоненты смещения здесь надо использовать составляющие, соответствующие координате .

11. Формулировка исходной задачи для численного решения

Итак, полная система уравнений для зависящих от времени намагниченностей и смещений содержит шесть уравнений первого порядка для компонент намагниченности вида (7) и уравнений второго порядка (26)-(28) для функций смещений . Используя стандартную процедуру сведения одного уравнения второго порядка к двум уравнениям первого порядка [32,33], из этих последних уравнений получаем уравнений первого порядка. Таким образом, полная система уравнений первого порядка для намагниченностей и упругих смещений, пригодная для численного решения, будет содержать уравнений, где – число членов ряда разложения по собственным функциям однородной задачи.

Контрольная проверка, подобная проведенной в работе [24], показывает, что с точностью до можно ограничиться первыми членами разложения, то есть приближением первой упругой моды. При этом в выражениях (24)-(33) надо положить , в результате чего уравнений для упругости останется , а полное число уравнений первого порядка составит . Явный вид подобной системы приведен в работе [24].

В настоящей работе именно такая система решалась численно методом Рунге-Кутта четвертого порядка [34]. При решении полагалась намагниченность слоя (подложки) на пять порядков меньшей намагниченности слоя (пленки), а также константа магнитоупругости (подложки) полагалась равной нулю. Какое-либо аналитическое условие на малость толщины слоя (пленки) по сравнению с толщиной слоя (подложки) не накладывалось, что позволило их варьировать в довольно широких пределах. Результаты расчетов приведены далее.

12. Основные численные параметры задачи

В следующих далее расчетах для более рельефного выявления наблюдаемых особенностей константу магнитоупругого взаимодействия в пленке будем полагать кратной такой константе для ЖИГ, то есть , где [6], а – целое число, соответствующее порядку кратности. Остальные параметры материала пленки возьмем соответствующими ЖИГ [6]: , , . Упругие параметры подложки и будем считать совпадающими с таковыми в пленке.

Важным предметом настоящего рассмотрения будет влияние диссипативных свойств подложки на магнитные и упругие процессы в структуре в целом. Принимаемые при этом параметры затухания магнитных и упругих колебаний будут указаны по ходу текста.

Толщину пленки возьмем равной , а полную толщину структуры – , так что толщина пленки составляет от толщины структуры , а толщина подложки равна , то есть почти .

Параметры возбуждения магнитострикционного преобразователя положим следующими: , , , поляризация переменного поля – круговая (2).

Параметры возбуждения ротационного магнетометра положим следующими: , , , поляризация переменного поля – круговая (4).

13. Развитие магнитных и упругих колебаний в схеме магнитострикционного преобразователя

Обратимся сначала к схеме магнитострикционного преобразователя и рассмотрим развитие магнитных и упругих колебаний во времени, происходящее после включения переменного поля. Соответствующая картина иллюстрируется рис.3.

На рис.3а приведено развитие во времени (сплошная линия) и (точечная линия) компонент намагниченности в пленке. Сплошная утолщенная линия соответствует поперечной составляющей вектора намагниченности, то есть его проекции на плоскость :

. (34)

Видно, что обе компоненты намагниченности колеблются с частотой переменного поля , причем колебания повторяют колебания со сдвигом фазы на , а проекция является огибающей этих колебаний. Огибающая с точностью не хуже описывается следующей эмпирической формулой:

. (35)

Рис.3. Развитие во времени магнитных (а) и упругих (б,в) колебаний пленки (а,б) и подложки (в). Тонкие сплошные линии – -компоненты; точечные линии – -компоненты; утолщенные сплошные линии – модуль намагниченности и смещения в плоскости . Параметры: , ; , остальные параметры приведены в разделе №12.

Время установления до уровня от максимума составляет около . Контрольная проверка показывает, что время установления магнитных колебаний обратно пропорционально параметру магнитного затухания и от параметра упругого затухания в пределах от до не зависит, то есть полностью определяется процессами магнитной диссипации.

На рис.3б приведено развитие во времени компонент упругого смещения , , а также поперечной составляющей

. (36)

на свободной поверхности пленки (то есть при , рис.1).

Можно видеть, что в этом случае упругие колебания повторяют магнитные с коэффициентом , определяемым величиной константы магнитоупругого взаимодействия . Амплитуда колебаний упругого смещения в установившемся режиме здесь составляет . Время установления – то же, что и для магнитных колебаний, то есть огибающая описывается формулой:

. (37)

На рис.3в приведено развитие во времени компонент упругого смещения , , а также поперечной составляющей

. (38)

на свободной поверхности подложки, противоположной пленке (то есть при , рис.1). Здесь поведение компонент , , а также существенно отличается от таких же компонент для пленки. Каждая из них содержит две составляющие, по характеру зависимости от времени их можно охарактеризовать как «медленную» и «быструю».

Медленная составляющая представляет собой смещение в одном направлении (по рисунку вниз), развивающееся в соответствии с законом, определяемым с точностью не хуже следующей эмпирической формулой:

. (39)

То есть можно полагать, что здесь имеет место сдвиговая деформация подложки в одном направлении, представляющая собой как бы установление равновесного состояния.

Медленная составляющая по величине примерно равна от , то есть в пределах точности рисунка практически отсутствует. При этом медленная составляющая , практически повторяя по амплитуде компоненту , отклоняется вверх в соответствии с положительностью модуля.

Контрольная проверка показывает, что время установления медленной составляющей обратно пропорционально параметру затухания упругих колебаний и от параметра затухания колебаний намагниченности практически не зависит, то есть определяется чисто упругими процессами релаксации.

Кроме этой медленной составляющей смещение содержит еще и налагающуюся на нее быструю, осциллирующую с частотой переменного поля. Амплитуда быстрой составляющей для всех трех кривых на рис.3в одинакова и составляет примерно . Развитие во времени быстрой составляющей происходит синхронно с развитием компонент намагниченности, то есть приближается к закону, определяемому формулой:

. (40)

Контрольная проверка показывает, что время установления быстрых колебаний обратно пропорционально параметру магнитного затухания и от параметра упругого затухания в пределах от до не зависит, то есть, так же как и установление колебаний намагниченности, полностью определяется процессами магнитной диссипации.

Таким образом, смещение подложки на стороне, противоположной пленке, представляет собой совокупность двух процессов: медленного установления равновесной сдвиговой деформации с постоянной времени, определяемой упругой диссипацией, в сочетании с быстрыми колебаниями, определяемыми частотой переменного поля, вокруг этой сдвиговой деформации с постоянной времени, определяемой магнитной диссипацией.

14. Ориентация деформации сдвига подложки

Из рис.3в видно, что равновесная медленная сдвиговая составляющая упругого смещения на стороне подложки имеет в плоскости вполне определенную ориентацию. Так сдвиговое смещение вдоль оси составляет , тогда как вдоль оси – всего около .

В то же время, в плоскости кристаллографическая структура подложки имеет квадратную симметрию с ориентацией боковых сторон квадрата вдоль осей и , то есть по величине плотности энергии (6) направления и полностью эквивалентны. Таким образом, энергии сдвиговой деформация подложки вдоль осей и между собой равны, то есть ориентация такой деформации в плоскости является неопределенной.

С целью выяснения причины установления определенной сдвиговой ориентации подложки в плоскости , было исследовано влияние на эту ориентацию начальных условий возбуждения, иллюстрируемое рис.4.

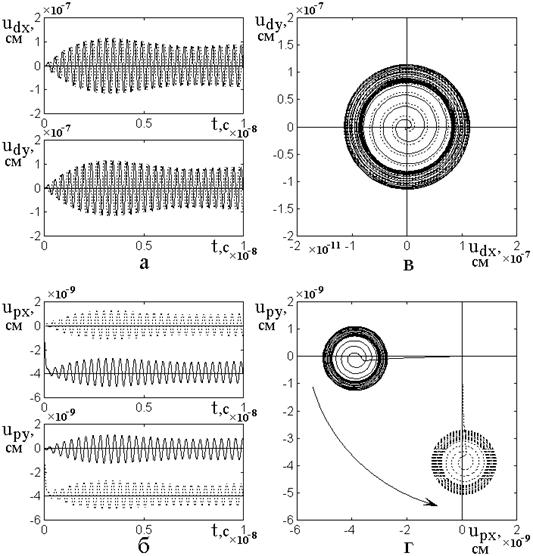
На рис.4 показано развитие колебаний упругого смещения на стороне пленки (а) и подложки (б), а также соответствующие им параметрические портреты (в,г) при двух различных фазах возбуждения, различающихся на .

Рис.4. Развитие колебаний упругого смещения на стороне пленки (а) и подложки (б), а также соответствующие им параметрические портреты (в,г) при различных фазах возбуждения.

Параметры: , , , остальные параметры – те же, что в разделе №12.

Сплошные линии соответствуют:

, , (41)

пунктирные:

, , (42)

то есть пунктирные – опережают сплошные по фазе на . Константа магнитоупругого взаимодействия и параметр упругого затухания здесь взяты несколько большими (, ), чем при построении рис.3, что сделано для более наглядного выявления роли быстрой составляющей. При этом амплитуда быстрых колебаний увеличилась до , а время установления медленной составляющей на уровне уменьшилось до . Величина медленной сдвиговой составляющей упругого смещения на стороне подложки осталась прежней – около .

Верхняя пара рисунков (а,в) соответствует упругим колебаниям на свободной поверхности пленки. Видно, что в этом случае колебания относительно осей и идентичны друг другу со сдвигом фаз на , отражающим сдвиг фазы возбуждения. Параметрический портрет представляет собой развивающуюся из центра спираль, переходящую в концентрические кольца геометрически правильной круговой формы. Такое поведение упругих колебаний на стороне пленки, подобно рис.3б, соответствует полному повторению развития магнитных колебаний, круговая симметрия которых была отмечена при рассмотрении рис.3а.

Нижняя пара рисунков (б,г) соответствует упругим колебаниям на поверхности подложки, противоположной пленке. Видно, что в этом случае быстрые колебания во всех случаях остаются одинаковыми, кроме сдвига фазы относительно друг друга на , что отражает сдвиг фазы как поля возбуждения, так и колебаний намагниченности на те же углы, благодаря круговой поляризации поля и намагниченности. Однако медленные сдвиговые составляющие по осям и здесь как бы меняются местами, как это наблюдается из верхней и нижней эпюр на рис.4б. При этом параметрический портрет таких колебаний испытывает поворот на , как это показано стрелкой на рис.4б.

Быстрые колебания в обоих случаях по-прежнему образуют правильные круговые кольца, подобные показанному на рис.4в, тогда как центр этих колец смещается из положения, соответствующего , , в новое положение, соответствующее , . Можно видеть, что эти центры как раз соответствуют величине медленного сдвигового смещения на верхней и нижней эпюрах рис.4б.

Таким образом, из проведенного рассмотрения следует, что ориентация медленного сдвигового смещения, будучи в энергетическом отношении произвольной, определяется начальной фазой переменного возбуждающего поля. Контрольная проверка показывает, что при добавлении к фазам обеих компонент возбуждающего поля одного и того же значения фазового угла, весь параметрический портрет поворачивается вокруг нуля координат как целое на тот же угол (с учетом знака добавляемого угла).

Замечание. Вообще говоря, определение ориентации сдвиговой деформации подложки фазой возбуждающего поля, не является однозначным, так как означает привязку начала колебаний к определенному моменту времени. То есть неопределенность ориентации остается в той же мере, в какой является неопределенной привязка фазы к началу процесса. В реальном случае включение поля не может быть осуществлено мгновенно, а развивается постепенно с какой-то постоянной времени, определяемой процессами релаксации в подводящих цепях. При этом фаза переменного поля относительно начального момента включения может быть подвержена случайным флуктуациям неопределенного характера, в результате чего установившаяся ориентация сдвиговой деформации также может иметь разное направление.

15. Некоторые свойства сдвиговой составляющей смещения подложки

Приведем некоторые свойства сдвиговой составляющей упругого смещения подложки. Будем полагать , , , а остальные параметры – как в разделе №12.

Прежде всего отметим, что явление сдвига является чисто динамическим: при выключении возбуждения какой-либо сдвиг отсутствует. То есть сдвиговая деформация подложки статической спонтанной деформацией за счет поля магнитострикции пленки не является. Действительно, пленка составляет лишь незначительную часть объема подложки (порядка ), а сама подложка магнитострикции не имеет, поэтому даже образование магнитоупругой щели в спектре колебаний пленки [35], хотя и возможно, но заметно изменить состояние подложки не должно.

Проведенное в разделах №13 и №14 рассмотрение относится к случаю ориентации постоянного поля точно по нормали к плоскости пленки. Так было показано, что столь незначительное нарушение симметрии, как изменение фазы возбуждающего поля, приводит к значительному изменению сдвиговой составляющей упругого смещения на стороне подложки. Дополнительное исследование показало, что при неизменной фазе возбуждающего поля значительный поворот портрета может вызвать небольшое нарушение симметрии постоянного поля, такое как его незначительное отклонение от нормали к плоскости пленки. Так добавление к нормальному полю, равному , дополнительного постоянного поля вдоль оси напряженностью в вызывает поворот параметрического портрета в положительную сторону (по часовой стрелке) на , а при поле в угол поворота увеличивается до . Приложение таких же полей отрицательного знака вызывает такой же поворот портрета в отрицательном направлении. Добавление поля вдоль оси той же величины приводит к подобному повороту портрета в противоположном направлении. Дальнейшее увеличение постоянного поля в плоскости пленки до приводит к превращению кругового портрета в вытянутый эллипс, а при еще большем увеличении портрет превращается в синусоиду с уменьшающимся периодом, что отражает стремление вектора намагниченности к переориентации, подобной описанной в работе [26].

Перечислим еще некоторые свойства сдвиговой составляющей упругого смещения подложки. Так было выявлено, что величина сдвига линейно зависит от амплитуды возбуждающего поля. При амплитуде сдвиг составляет , при амплитуде равняется , а при амплитуде достигает . Величина сдвига линейно зависит от величины константы магнитоупругого взаимодействия. Так при сдвиг составляет , при увеличивается до , а при достигает . При увеличении параметра упругого затухания величина сдвига уменьшается, причем не линейным образом, а заметно быстрее. Так при сдвиг составляет , при уменьшается до , а при падает до Приведенные свойства дополнительно свидетельствуют в пользу динамической природы явления.

16. Общие свойства колебаний в схеме магнитострикционного преобразователя

Из проведенного рассмотрения можно видеть, что в схеме магнитострикционного преобразователя в нерезонансном случае вклад диссипации упругой системы в диссипацию магнитной системы, если и существует, то весьма незначителен по сравнению со вкладом от собственных процессов магнитной релаксации. Благодаря массивности подложки по сравнению с пленкой, колебания последней происходят так, как если бы пленка на границе с подложкой имела жесткое закрепление. Упругая волна, распространяясь по толщине подложки, испытывает ослабление, определяемое процессами упругой релаксации в самой подложке. В результате, амплитуда упругих колебаний на стороне подложки, противоположной пленке, становится значительно меньше амплитуды упругих колебаний на стороне пленки.

Подложка, кроме колебаний, синхронных с возбуждающем полем, испытывает определенную квазистатическую сдвиговую деформацию, ориентация которой в плоскости пленки может определяться как фазой возбуждающего поля, так и сравнительно небольшим отклонением постоянного поля от нормали к плоскости пленки.

17. Развитие магнитных и упругих колебаний в схеме ротационного магнетометра

Обратимся теперь к схеме ротационного магнетометра и рассмотрим развитие магнитных и упругих колебаний во времени, происходящее после включения переменного поля. В работах [14,15] показано, что в схеме ротационного магнетометра упругая диссипация в значительной степени определяет магнитную, чем оказывает определенное влияние на уровень шума и чувствительность магнетометра. Эти работы относятся к случаю возбуждения колебаний намагниченности и упругого смещения в условиях, близких к резонансным.

Однако в типичных случаях ротационный магнетометр работает на частоте не выше единиц МГц, то есть по крайней мере на два порядка ниже частоты ФМР в поле размагничивания пластины. Толщина подложки тоже, как правило, недостаточна для резонанса на этих частотах. Поэтому представляет интерес рассмотреть влияние упругой диссипации на работу ротационного магнитометра при возбуждении на частоте значительно ниже резонансных частот как для намагниченности, так и для упругого смещения.

Соответствующая картина иллюстрируется рис.5. Для более четкого выявления степени влияния упругой диссипации на магнитную, параметр магнитного затухания выбран заведомо малым: , то есть по крайней мере на порядок меньшим, чем для лучшего ЖИГ.

Рис.5. Развитие во времени магнитных (а,б,в) и упругих (г,д,е) колебаний в схеме ротационного магнетометра при различных значениях параметра упругого затухания:

а,г – ; б,д – ; в,е – .

Параметры: , , остальные параметры указаны в разделе №12.

На рис.5 показано развитие во времени магнитных и упругих колебаний, происходящее с момента включения переменного поля, при различных значениях параметра упругого затухания. За основу рассмотрения магнитных колебаний принята х-компонента намагниченности, а для упругих колебаний рассмотрена общая длина вектора упругого смещения, определяемая формулой (36).

Из рис.5а,б,в видно, что основу магнитных колебаний составляет синусоида с периодом , что соответствует частоте возбуждающего переменного поля, равной . Компонента меняется в пределах от до . Проверка показывает, что компонента колеблется подобным же образом со сдвигом фазы на , то есть вращение намагниченности происходит по кругу в плоскости пленки, следуя за переменным полем.

На такие медленные колебания накладываются быстрые, период которых определяется частотой ФМР в поле размагничивания пленки и составляет около . Амплитуда таких быстрых колебаний, составляющая в начале возбуждения , затухает с постоянной времени около , падая при до

Из взаимного сравнения рис.5а,б,в можно видеть, что развитие во времени магнитных колебаний (как медленных, так и быстрых) при изменении упругого затухания не меняется (с точностью рисунка, не менее ), то есть можно полагать, что оно определяется только параметром магнитного затухания , в формировании которого упругое затухание участия не принимает.

Этот вывод совпадает с аналогичным заключением, сделанным при рассмотрении рис.3а в разделе №13, относящемся к магнитострикционному преобразователю.

Рассмотрим теперь упругие колебания. Из рис.5г,д,е можно видеть, что с течением времени на стороне пленки упругие колебания при всех значениях параметра затухают. При малом упругом затухании (рис.5г) спад амплитуды упругих колебаний происходит с биениями, по-видимому, обусловленными рассогласованием частоты возбуждения с резонансной частой подложки. Однако при среднем и большом затухании (рис.5д,е) биения уже отсутствуют, а спад амплитуды происходит с той же постоянной времени, примерно соответствующей таковой для затухания быстрых колебаний компоненты намагниченности (рис.5а,б,в). То есть можно полагать, что при параметре упругого затухания больше движение упругого смещения уже самостоятельности не проявляет, а следует за колебаниями намагниченности.

При малом затухании (рис.5г) установление упругого смещения происходит с небольшим сдвигом во времени, составляющим около , тогда как при среднем и большом затухании (рис.5д,е) такой сдвиг отсутствует. Можно полагать, что отсутствие сдвига в этом случае обусловлено увеличением инертности подложки по мере увеличения затухания, то есть пленка уже колеблется так, как будто бы подложка была неподвижной и ее колебания заметного влияния на состояние подложки не оказывают.

Исследование упругих колебаний на свободной стороне подложки показывает, что здесь они ведут себя подобно таковым в схеме магнитострикционного преобразователя (раздел №13). В данном случае они практически не содержат ни быстрой, ни медленной составляющей, однако во всех случаях имеется стационарный сдвиг. Величина такого сдвига при составляет около , при – , при – , то есть уменьшается примерно пропорционально увеличению параметра упругого затухания, аналогично случаю магнитострикционного преобразователя (раздел №13).

Установление сдвига при малом затухании происходит за время порядка , а при среднем и большом – практически сразу после включения возбуждения, точнее за время, меньшее чем , то есть за всего несколько периодов быстрых колебаний намагниченности. Такой характер поведения времени установления сдвига говорит о решающей роли упругого затухания без какого-либо участия магнитного, что вполне согласуется со случаем магнитострикционного преобразователя (раздел №13).

Заключение

Рассмотрено возбуждение магнитоупругих колебаний в структуре «магнитная пленка – немагнитная подложка», когда толщина подложки значительно превышает толщину пленки, то есть в отсутствие как магнитного, так и упругого резонансов. Рассмотрение проведено на примере схем магнитострикционного преобразователя и ротационного магнетометра, отличающихся по структуре постоянного и частоте переменного поля.

Главным результатом настоящей работы является вывод о том, что вклад диссипации упругой системы в диссипацию магнитной системы незначителен и решающим, в отличие от резонансного случая, не является. То есть диссипация магнитной системы (пленки) определяется не диссипацией упругой системы (подложки), а в первую очередь внутренними процессами магнитной релаксации в самой пленке.

Далее, можно полагать, что благодаря массивности подложки по сравнению с пленкой, колебания последней в значительной степени происходят так, как если бы пленка на границе с подложкой имела бы сравнительно жесткое закрепление. То есть энергия упругих колебаний пленки передается в подложку со значительным ослаблением, что приводит к уменьшению амплитуды упругих колебаний подложки по сравнению с пленкой. При этом упругая волна, возбужденная в подложке на границе ее с пленкой, распространяясь по толщине подложки, испытывает дополнительное ослабление, определяемое процессами упругой релаксации в самой подложке. В результате, амплитуда упругих колебаний на стороне подложки, противоположной пленке, становится меньше амплитуды упругих колебаний на свободной стороне пленки, причем такое уменьшение может достигать нескольких порядков.

Подложка, кроме колебаний, синхронных с возбуждающем полем, испытывает определенную квазистатическую сдвиговую деформацию, причиной которой является динамический процесс колебаний в пленке. Ориентация такой сдвиговой деформации в плоскости пленки может определяться как фазой возбуждающего поля, так и сравнительно небольшим отклонением постоянного поля от нормали к плоскости пленки.

Работа выполнена при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).

Литература

1. Адам Дж.Д. // ТИИЭР. 1988. Т.76. №2. С.73.

2. Исхак В.С. // ТИИЭР. 1988. Т.76. №2. С.86.

3. Adam J., Davis L., Dionne G., Schloemann E., Stitzer S. // IEEE Trans. on MTT. 2002. V.50. №3. P.721.

4. Кикучи Е. // Ультразвуковые преобразователи. М.: Мир. 1972.

5. Голямина И.П. // Магнитострикционные излучатели из ферритов. В кн.: Физика и техника мощного ультразвука. Кн.1. Источники мощного ультразвука. М., Наука, 1967.

6. Ле-Кроу Р., Комсток Р. // В кн.: У. Мэзон (ред.): Физическая акустика. Т.3Б. Динамика решетки. М.: Мир. 1968. С.156.

7. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2009. Т.54. №7. С.863.

8. Ветошко П.М. // Магнитометр. Патент № 21000819. Приоритет от 30.09.1996.

9. Никитин П.И., Ветошко П.М. // Измеритель магнитной восприимчивости. Патент РФ № 2177611. Приоритет от 09.03.2000.

10. Vetoshko P.M., Valeiko M.V., Nikitin P.I. // Sensors and Actuators A. 2003. V.106. №1-3. P.270.

11. Nikitin P.I., Vetoshko P.M., Ksenevich T.I. // J. Magn. Magn. Mat. 2007. V.311. P.445.

12. Skidanov V., Vetoshko P. // Procedia Enineering. 2010. V.5. P.989.

13. Vetoshko P., Skidanov V., Stempkovskiy A. // Sensor Letters. 2013. V.11. P.59.

14. Ветошко П.М., Шавров В.Г., Щеглов В.И. // Электронный "Журнал радиоэлектроники". 2014. №11. http://jre.cplire.ru/jre/nov14/1/text.html,

http://jre.cplire.ru/jre/nov14/1/text.pdf.

15. Ветошко П.М., Шавров В.Г., Щеглов В.И. // Сборник трудов XXII Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2014. С.237.

16. Моносов Я.А. // Нелинейный ферромагнитный резонанс. М.: Наука. 1971.

17. Захаров В.Е., Львов В.С., Старобинец С.С. // УФН. 1974. Т.114. №4. С.609.

18. Temiryazev A.G., Tikhomirova M.P., Zilberman P.E. // J. Appl. Phys. 1994. V.76. №12. P.5586.

19. Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ЖЭТФ, 1995. Т.108. №1. С.281.

20. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // РЭ. 1999. Т.44. № 10. С.1262.

21. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ФТТ. 2000 Т.42. №6. С.1062.

22. Gerrits Th., Schneider M.L., Kos A.B., Silva T.J. // Phys.Rev.B. 2006. V.73. №9. P.094454(7).

23. Семенцов Д.И., Шутый А.М. // УФН. 2007. Т.177. № 8. С.831.

24. Власов В.С., Шавров В.Г., Щеглов В.И. // Электронный "Журнал радиоэлектроники". 2013. №2. http://jre.cplire.ru/jre/feb13/10/text.html, http://jre.cplire.ru/jre/feb13/10/text.pdf.

25. Власов В.С., Шавров В.Г., Щеглов В.И. // РЭ. 2014. Т.59. №5. С.482.

26. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2010. Т.55. №6. С.689.

27. Власов В.С., Иванов А.П., Шавров В.Г., Щеглов В.И. // Сборник трудов XXI Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2013. С.188.

28. Власов В.С., Иванов А.П., Шавров В.Г., Щеглов В.И. // Электронный "Журнал радиоэлектроники". 2014. №1. http://jre.cplire.ru/jre/jan14/11/text.html,

http://jre.cplire.ru/jre/jan14/11/text.pdf.

29. Власов В.С., Иванов А.П., Шавров В.Г., Щеглов В.И. // РЭ. 2015. Т.60. №1. С.79.

30. Власов В.С., Иванов А.П., Шавров В.Г., Щеглов В.И. // РЭ. 2015. Т.60. №3. С.297.

31. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука. 1972.

32. Степанов В.В. Курс дифференциальных уравнений. М.,Л.: ОГИЗ. Гос. изд. техн.-теор. лит. 1945.

33. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука. 1965.

34. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука. 1973.

35. Туров Е.А., Шавров В.Г. // ФТТ. 1965. Т.7. №1. С.217.