| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 8, 1999 |
Новый метод
аналитического решения двухмерных задач
теории дифракции
М.В. Весник,
Институт радиотехники и
электроники РАН
Получена 9 августа 1999 г.
Предложен новый метод решения двухмерных краевых задач теории дифракции на идеально проводящих полубесконечных телах. Метод основан на построении с помощью теории конформных отображений универсального интегрального представления дифракционной части решения, которое в сумме с геометрооптическими составляющими падающей и отраженной волн представляет собой решение краевой задачи уравнения Гельмгольца. Получено строгое решение для полубесконечных тел с многоугольной огибающей. Построены асимптотики интегрального представления в компактной, удобной для дальнейшего применения форме.
1. Введение
К настоящему моменту строгие аналитические решения краевых задач в теории дифракции получены либо методом разделения переменных, либо методом Винера-Хопфа или его модификациями, причем число таких решений невелико. В данной работе предлагается новый метод, который позволяет увеличить число строгих двухмерных решений теории дифракции.
2. Постановка задачи
Требуется найти решение двухмерной задачи рассеяния волны
Рис. 1 Области
Решение для дифракционной волны
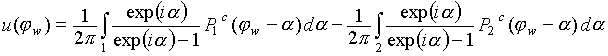 |
(1) |
смысл остальных обозначений будет объяснен ниже.
3. Построение интегрального представления и асимптотик решения
Будем считать, что по оси ![]() откладываются мнимые величины, и таким образом
плоскость
откладываются мнимые величины, и таким образом
плоскость ![]() является комплексной.
С помощью теории функций комплексного
переменного можно найти взаимно однозначное
конформное отображение области
является комплексной.
С помощью теории функций комплексного
переменного можно найти взаимно однозначное
конформное отображение области ![]() ,
представляющей собой верхнюю полуплоскость
комплексной плоскости
,
представляющей собой верхнюю полуплоскость
комплексной плоскости ![]() , на область
, на область ![]() ,
представляющую собой внешность рассеивателя в
комплексной плоскости
,
представляющую собой внешность рассеивателя в
комплексной плоскости ![]() :
:
|
(2) |
Функции (2) соответствует обратная функция:
|
(3) |
причем даже если выражение (3) не существует в явном виде, то, задавая
Ограничимся рассмотрением случая возбуждения плоской волной, приходящей с направления
|
(4) |
однако предлагаемая методика применима и для других типов возбуждения.
Запишем (2) в полярных координатах
|
(5) |
Здесь
|
(6) |
Для точки наблюдения с координатами
|
(7) |
Введем новые комплексные переменные
|
(8) |
где
Рис. 2 Область
Зададим на множестве комплексных значений
|
(9) |
Обозначим введенные ранее области
До сих пор переменные, не имеющие индекса "1" или"2":
Преобразуем область
Рассмотрим теперь интегральное представление (1), для которого пути интегрирования "1" и "2" в области a таковы, что соответствующие им точки области
Можно показать, что интегральное представление (1) удовлетворяет волновому уравнению и условию на бесконечности, а также является непрерывной по переменной
Построим функцию
|
(10) |
Здесь под функцией
|
(11) |
удовлетворяет граничным условиям Дирихле или Неймана соответственно и таким образом является искомым решением нашей краевой задачи. Это решение является строгим для случая тел с многоугольной огибающей. Для тел отличной формы требуется дополнительное математическое исследование точности
решения.Получим теперь асимптотическое выражение интегрального представления (1) при
|
(12) |
Тогда, поскольку
|
(13) |
Окончательные выражения будут такими:
где 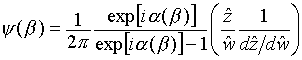 |
(14) |
Асимптотическое выражение для случая двух границ "свет - тень" будет таким:
|
(15) |
где
Проанализировав полученное выражение, можно видеть, что оно представляет собой сумму членов, связанных с седловыми точками, находящимися на границах тени падающей и отраженной волн. Границы тени расходятся от одной точки на поверхности рассеивателя, но расположены в разных листах
.4. Алгоритм поиска решения
Итак, имеется следующая постановка задачи: двухмерный рассеиватель произвольной формы, облучаемый плоской (или другой) волной и точка наблюдения. Необходимо найти решение краевой задачи. В соответствии с разработанной методикой можно предложить следующий алгоритм поиска решения:
1. Находим конформное отображение (2),
определяющее пути интегрирования 1 и 2 в области ![]() .
Как только мы это сделали, уже можно записать
решение для расходящейся части краевой задачи в
интегральной форме (1). Если нас интересует
асимптотика, нужно делать дальнейшие шаги.
.
Как только мы это сделали, уже можно записать
решение для расходящейся части краевой задачи в
интегральной форме (1). Если нас интересует
асимптотика, нужно делать дальнейшие шаги.
2. Находим седловые точки ![]() функции
функции ![]() (9).
(9).
3. Находим
4. Записываем решение в соответствии с формулой (11).
5. Пример применения метода для случая дифракции на клине
В качестве примера применения предлагаемого
метода получим известное решение для рассеяния
плоской волны (4) на идеально проводящем клине,
внешний угол которого равен ![]() радиан. Для этого пройдем все
шаги нашего алгоритма:
радиан. Для этого пройдем все
шаги нашего алгоритма:
1. Конформное отображение (1): ![]() . Обратная
функция (3):
. Обратная
функция (3): ![]() , откуда для точки
, откуда для точки ![]() получаем:
получаем: ![]() , а из (8) следует:
, а из (8) следует: ![]()
2. Седловые точки функции
3. Производная (12):
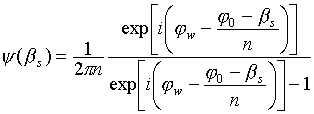 .
.
Отсюда легко получается выражение (15), которое полностью совпадает с известным решением для клина [2].
6. Заключение
В данной работе предложен новый метод аналитического решения двухмерных задач дифракции, с помощью которого получено решение для случая падения плоской волны на полубесконечный рассеиватель. С помощью этого метода было получено строгое решение для случая рассеяния плоской волны на полупластине (конечной толщины) [3]. По-видимому, не существует ограничений, препятствующих применению этой же методики для случая других возбуждающих волн и других типов двухмерных рассеивателей, например многосвязных или ограниченного размера. Кроме универсальности предлагаемого метода можно также отметить его большое удобство, так как если известно конформное отображение (2), то построение аналитической формулы для асимптотики решения соответствующей краевой задачи сводится лишь к вычислению производной (12).
Автор выражает благодарность проф. В.А.Калошину за полезные советы при подготовке этой публикации.
Литература
[1] Франк Ф., Мизес Р. Дифференциальные и интегральные уравнения математической физики. ОНТИ, 1937.
[2] Pauli W. On asymptotic series for functions in the theory of diffraction of light. Physical Review, 54, № 11, 924-931, 1938.
[3] М.В. Весник "Аналитическое решение краевой задачи для уравнения Гельмгольца". Радиотехника и электроника, 2000, том 45, № 1, стр. 66-76.
Автор: Весник Михаил , e-mail: vesnik@mail.cplire.ru