| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 12 , 2000 |
ВЕКТОРНАЯ СТРУКТУРА ИЗЛУЧЕНИЯ, ОТРАЖЕННОГО ЛЕСНЫМ ПОКРОВОМ ЗЕМЛИ
В. П. Якубов, Е.
Д. Тельпуховский, В. Д.Чуйков,
М. Г. Булахов, Д. В. Малышев
Томский государственный университет
Получена 8 декабря 2000 г.
Исследуются особенности отражения волн двух ортогональных поляризаций от лесного покрова Земли. На этой основе предлагается метод определения электрофизических параметров и средней высоты леса. Для измерения значений коэффициентов отражения предполагается использовать векторную антенну, регистрирующую в одной точке одновременно все шесть компонент электромагнитного поля.
1. Введение
В последнее время усилился интерес к аэрокосмическим методам исследования поверхности Земли, в частности лесных покровов. Основным инструментом при этом является искусственное и естественное электромагнитное излучение радиодиапазона [1]. Для этого диапазона лес полупрозрачен. Это значит, что в отличие от оптического диапазона с помощью радиоволн его можно исследовать на всю глубину, что особенно важно, например, для экологического мониторинга лесов как “легких планеты”. Для правильной интерпретации данных аэрокосмического мониторинга лесных покровов необходима адекватная модель взаимодействия радиоизлучения с лесом, разработка которой незавершенна до настоящего времени. Наибольшие надежды при зондировании лесов связываются с использованием контрастов в отражении волн ортогональных поляризаций [1]. Предлагаемая работа имеет своей целью провести теоретический анализ одного из возможных вариантов зондирования лесных покровов.
2. Анализ отражения радиоизлучения от
лесного покрова и метод решения обратной задачи
Не претендуя на универсальность подхода, в настоящей работе мы будем
рассматривать лес как случайно неоднородный плоский слой, имеющий толщину ![]() , с усредненными электрофизическими характеристиками
(проницаемостью
, с усредненными электрофизическими характеристиками
(проницаемостью ![]() и проводимостью
и проводимостью ![]() ). Справедливость такого подхода для различных типов лесов
обоснована в работе [2] сопоставлением экспериментальных данных по распространению
радиоволн в лесных массивах с теоретическими оценками. При аэрокосмическом
зондировании лесного покрова уместно считать, что верхняя граница лесного слоя
имеет неровную границу с дисперсией разброса высот
). Справедливость такого подхода для различных типов лесов
обоснована в работе [2] сопоставлением экспериментальных данных по распространению
радиоволн в лесных массивах с теоретическими оценками. При аэрокосмическом
зондировании лесного покрова уместно считать, что верхняя граница лесного слоя
имеет неровную границу с дисперсией разброса высот ![]() . Среднюю высоту слоя обозначим, как
. Среднюю высоту слоя обозначим, как ![]() . Для упрощения задачи будем полагать, что электрофизические
параметры подстилающей земной поверхности (
. Для упрощения задачи будем полагать, что электрофизические
параметры подстилающей земной поверхности (![]() и
и ![]() ) известны. Согласно [3, 4] коэффициент отражения
монохроматической волны с волновым числом
) известны. Согласно [3, 4] коэффициент отражения
монохроматической волны с волновым числом ![]() по среднему полю для
плоско слоистой системы воздух-лес-земля равен
по среднему полю для
плоско слоистой системы воздух-лес-земля равен
Здесь первое
слагаемое в числителе описывает отражение от неровной границы раздела двух
полупространств воздух-лес, а второе слагаемое – отражение от границы
полупространств лес-земля. Знаменатель описывает всевозможные многократные
переотражения, возникающие между верхней и нижней границами слоя леса. При
таком подходе не учитываются лишь эффекты взаимного затенения неровной границы
воздух-лес, которые могут проявиться при углах падения ![]() волны, близких к
скользящим (
волны, близких к
скользящим (![]() ).
).
Будем считать, что показатель
преломления леса ![]() также как и земли
также как и земли ![]() связаны с
соответствующими усредненными электрофизическими параметрами с помощью
соотношений [5]:
связаны с
соответствующими усредненными электрофизическими параметрами с помощью
соотношений [5]:
![]() и
и ![]() .
.
При этом френелевские коэффициенты отражения леса и земли определяются как [3, 5]:
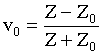 и
и 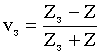 ,
,
где импедансы
сред ![]() зависят от
поляризации и направления распространения волны. Так полагают
[3], что для
горизонтальной поляризации
зависят от
поляризации и направления распространения волны. Так полагают
[3], что для
горизонтальной поляризации
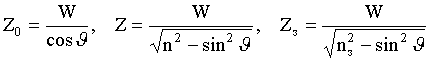 ,
,
а для вертикальной поляризации
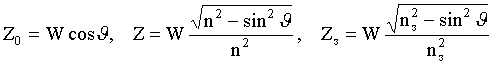 .
.
Здесь ![]() - волновое
сопротивление свободного пространства.
- волновое
сопротивление свободного пространства.
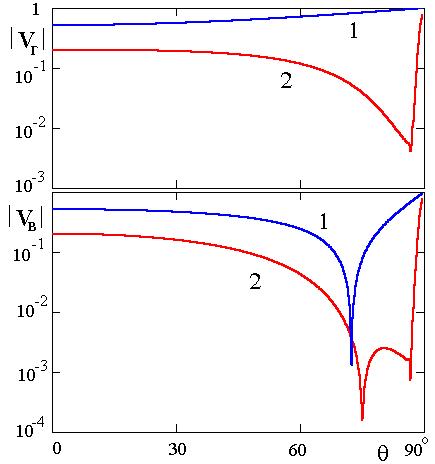
Результаты расчетов зависимости коэффициентов отражения от угла падения
волны по приведенным выше формулам представлены кривыми 2 на
рис. 1. Расчеты
проводились для излучения с длиной волны ![]() . При этом для земли приняты значения электрофизических
параметров [5]:
. При этом для земли приняты значения электрофизических
параметров [5]:![]() и
и ![]() . Для леса согласно [2] взяты значения:
. Для леса согласно [2] взяты значения:![]() и
и ![]() . Средняя высота леса взята
. Средняя высота леса взята ![]() . Разброс высот неровностей верней границы леса оценивается
как
. Разброс высот неровностей верней границы леса оценивается
как ![]() . Заметим, что, начиная с этого значения, увеличение разброса
высот не влияет на результат.
. Заметим, что, начиная с этого значения, увеличение разброса
высот не влияет на результат.
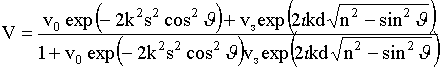 .
.

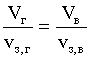 ,
,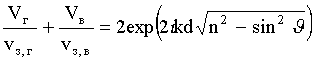 .
.
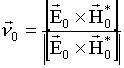
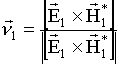 .
.