"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 11, 2001

оглавление

дискуссия

 

Оценка точности измерения углов прихода волны в декаметровом диапазоне волн

 

В. В. Копытов, О. Г. Пикалов

филиал Ростовского военного института РВ, г. Ставрополь

 

Получена 7 декабря 2001 г.

 

Оценены погрешности определения координат источника радиоизлучения по углам прихода однолучевого сигнала, вызванные искажением фазового фронта волны, за счет неоднородностей ионосферы на основе теории фазового экрана.

 

введение

 

Быстрое развитие многих отраслей народного хозяйства сопровождается повышением требований к точности определения координат объектов на поверхности Земли.

Одной из важнейших проблем, связанных с повышением качества радиоэлектронных измерительных систем (интерферометров - радиопеленгаторов с широкобазисными антеннами) является совершенствование методов оценки их точности. Имеющиеся публикации [1, 2] по оценке точности определения координат источника радиоизлучения в декаметровом диапазоне волн посвящены в основном анализу инструментальной (аппаратурной) s_и среднеквадратической погрешности, среднеквадратической погрешности обусловленной шумами (помехами) s_ш и среднеквадратической погрешности измерения действующей высоты отражающего ионосферного слоя s_hд. Для существующих радиопеленгаторов суммарная погрешность равна [1, 2] 0,5 - 1 градус по углу места (j) и азимута (q), что в пересчете на координаты составляет около 20 - 30 км на местности.

Однако это справедливо только в том случае, если ионосфера является идеальным отражателем и практически не содержит неоднородностей. На практике [3] неоднородности ионосферы вносят существенные искажения в фазовый фронт волны, что приводит к погрешности определения углов прихода волны (s_a) при измерении интерферометром от 0,5 до 8 градусов. В этом случае погрешность определения углов прихода волны, за счет рассеивания в возмущенной ионосфере может существенно превышать погрешности s_и, s_ш, s_hд.

Цель работы - разработка научно-методического аппарата установления аналитической зависимости величины среднеквадратической погрешности определения местоположения источника радиоизлучения от трех факторов: физических параметров неоднородной ионосферы (максимальной средней электронной концентрации (`N(h_m)), интенсивности неоднородностей (b), их характерного размера (L_s)), выбора рабочей частоты и геометрии радиолинии.

Данный научно-методический аппарат позволит повысить объективность оценки точности определения координат источника радиоизлучения, за счет учета искажений принимаемых интерферометром радиосигналов на неоднородностях ионосферы на основе теории фазового экрана для каналов с замираниями [5].

 

1. ОСНОВНЫЕ МОДЕЛЬНЫЕ СООТНОШЕНИЯ

 

Для достижения цели работы необходимо:

оценить влияние среды распространения радиоволн на дисперсию флуктуаций фазы (s²_j) на входе интерферометра, т.е. показать ее зависимость от физических параметров неоднородной ионосферы (`N(hm), b, Ls), выбора рабочей частоты (f_о) и геометрии радиолинии (определяемой координатами источника радиоизлучения (j_n, l_n) и интерферометра (j_м, l_м)):

 

s²_j = Y{`N(h_m), b, L_s, f_о, j_n, l_n, j_м, l_м);                                           (1)

 

оценить влияние дисперсии s²_j на величину среднеквадратической погрешности определения углов прихода волны (s_a) при измерении интерферометром с базой (d):

 

s_a = Y{`N(h_m), b, L_s, f_о, j_n, l_n, j_м, l_м, d).                                          (2)

 

Существующий научно-методический аппарат на основе метода фазового экрана [4] позволяет оценить влияние дисперсии s²_j только на достоверность связи. При этом влияние s²_j  на точность определения координат источника радиоизлучения при измерении интерферометром не рассматривалось. Кроме того, для оценки точности определения координат источника радиоизлучения, помимо дисперсии s²_j, важно знать [5, 6] интервал пространственной корреляции поля (функцию пространственной корреляции поля R_j(d)) при наблюдении в двух точках, разнесенных по линии, перпендикулярной направлению прихода радиоволны. В работах [5, 6] приводятся выражения для погрешности определения углов прихода радиоволны (s_a) с учетом среднего значения коэффициента преломления (D`n²) при измерениях интерферометром для крайних случаев:

при базе интерферометра много больше функции пространственной корреляции d>>R_j(d):

 

s_a² = (p×D`n²L_э)/L_s;                                           (3)

 

при базе интерферометра много меньше функции пространственной корреляции d<<R_j(d):

 

s_a² = (p×D`n²L)/d×cosa×(1-exp(-(d×cosa/L_s)²)).                     (4)

 

Однако для декаметровых радиолиний значения интервала пространственной корреляции поля, равные [3] (10-25)l, могут быть сравнимы с базой интерферометра (d = 150-300 м). Соответственно, возникает необходимость в получении аналитической зависимости погрешности определения углов прихода волны при измерении интерферометром от дисперсии флуктуации фазы, функции пространственной корреляции поля и базы интерферометра:

 

s_a = Y{s²_j, R_j(d), d).                                  (5)

 

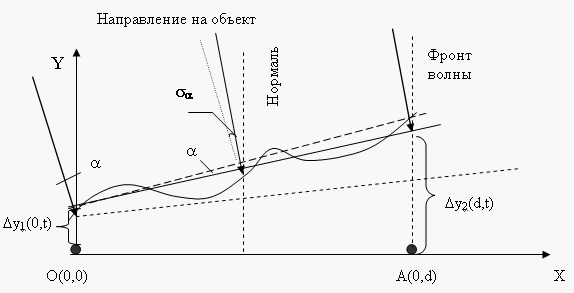
Решение поставленной задачи может быть осуществлено следующим образом. На рис. 1 приведена геометрическая интерпретация влияния дисперсии фазового фронта волны (s²_j) на среднеквадратическую погрешность определения углов прихода радиоволны в тангенциальном (s(Q)_a) и радиальном (s(j)_a) направлениях. При этом будем считать фронт падающей на интерферометр волны плоским с искажениями, определяемыми s²_j, причем при пересечении волны с плоскостью интерферометра ее кривизна меняется на противоположную. Угол падения плоской волны составляет a.

 

Рис. 1. Геометрическая интерпретация влияния s²_j на погрешности

s(Q)_a и s(j)_a.

 

Введем прямоугольную систему координат, ось Х совпадает с базой интерферометра (ОA), а ось Y перпендикулярна ей. Пусть в точках О(0,0) и А(0,d) расположены две антенны, образующие интерферометр. Путь луча, приходящего в точку А(0,d), есть Y = l+Dy₂(d,t). Измеряя сдвиг (разность) фаз Dj поля в двух точках пространства, разнесенных одна от другой на расстояние d, называемое базой, можно определить направление прихода радиоволн. Разность хода отраженной волны к разнесенным антеннам (рис.1) равна

 

DY=Dy₁-Dy₂.                                                      (6)

 

Рассмотрим случай нормального падения (азимутальная плоскость), когда волна падает не под углом, а параллельно оси Х, т.е. среднее направление распространения радиоволны совпадает с осью Oy. В этом случае

 

D`Y<sup>2</sup>=D`y₁² + D`y<sub>2</sub><sup>2</sup> - 2×D`y₁D`y₂.                                 (7)

 

Обозначив через D`y² средний квадрат флуктуации, выражение (7) можно записать в виде:

 

D`Y<sup>2</sup>=2D`y₁² - 2D`y<sub>2</sub><sup>2</sup>×R<sub>j</sub>(d) = 2D`y²×(1 - R_j(d).                    (8)

 

Из-за разности хода D`y² отраженной радиоволны к разнесенным антеннам возникает фазовое различие, которое можно характеризовать дисперсией флуктуаций фазы s_j², в принимаемых сигналах, которое будет равно

 

s_j² = k²×D`y²,                                      (9)

 

где k=2p/l - волновое число; l - длина волны.

В свою очередь разность хода отраженной волны связана с погрешностью определения угла прихода радиоволны s²_a при измерениях интерферометром, как

 

DU²=d²×tg(s²_a),                                            (10)

или при малом a

DU²=d²×s²_a.                                            (11)

 

C учетом (8, 9, 10) выражения для погрешности определения углов прихода волны в азимутальной плоскости s²(Q)_a при измерениях интерферометром, обусловленной флуктуациями фазового фронта волны, запишем в виде:

 

s²(Q)_a =arctg(2s_j²)/(k²d²)×(1-R_j(d)),                            (12)

 

Дисперсия флуктуации фазы (s_j²) в точке приема, вычисляется из [8]:

 

s_j² = s_jо²/2×(1 + 1/(1 + D^/2)).                                (13)

 

Здесь D^/=2z/kL_s² – параметр Горелика, характеризующий область фокусировок;

s_jо² - дисперсия флуктуации фазового фронта волны на выходе ионосферы с учетом характерного размера неоднородностей [4]

 

s_jо² = 2×L_эL_s[pK_sbf_о/(c×sinj_о)]²,                            (14)

 

с – скорость света в вакууме; K_s – коэффициент сферичности ионосферы;

L_э – эквивалентный путь ДКМ электромагнитной волны в слое F [4]:

 

L_э = (h_д(f_в)–h_о)×(1+K_sf_кр²/f_в²-z_mK_s/(h_д(f_в)–h_о)) ´

 

´ [secj_о²–1/2×(1+K_sf_кр2/f_в²-z_mK_s/(h_д(f_в) –h_о))]^1/2,                   (15)

 

где f_кр²/f_в² - отношение критической частоты к частоте вертикального зондирования (f_в = f_о/secj_о); z_m – полутолщина отражающего слоя; h_д – действующая высота отражения, определяемая согласно [9]:

 

h_д(f_в) = h_о+z_m/2×f_в/f_кр×ln(1+(f_в/f_кр)/(1-f_в/f_кр));                     (16)

 

j_о – угол падения излучаемой волны на нижнюю границу ионосферы, определяемый выражением:

 

j_о = arctg(sin(D/2R_з)/(1 + h_д(f_в)/R_з – cos(D/2R_з))).              (17)

 

Расстояние Z до области отражения можно найти из выражения:

 

z² = h_д(f_в)² + D²/4),                    (18)

 

где D – дальность до источника радиоизлучения по земной поверхности [9]:

 

D = R_З×y,                         (19)

 

а R_з- радиус Земли; y - угловое расстояние между источником радиоизлучения и интерферометром:

 

y = ((j_n²-j_м²)+(l_n²-l_м²))^1/2.                (20)

 

Пространственная корреляционная функция R_j(d) вычисляется как [4, 6]:

 

R_j(Δр_а/l) = exp(-((Δр_а/l)/(Δр_к/l))²),                  (21)

 

где Δр_а – интервал пространственного разноса, равный базе интерферометра;

Δр_к = l/((2p)^1/2×s_v² – интервал пространственной корреляции поля;

s_v² – дисперсия флуктуаций углов прихода волны в некоторой точке апертуры приемной антенны:

 

s_v² = 2s_j²/(2pL_s/l).                    (22)

 

С учетом (22) выражение (21) имеет вид:

 

R_j(d) = exp(-s_j²×(d/L_s)²).                      (23)

 

Таким образом, общее выражение для расчета погрешности определения угла азимута (s(Q)_a) при измерениях интерферометром запишется в виде:

 

s²(Q)_a =arctg(2s_j²)/(k²×d²)×(1- exp(-s_j²×(d/L_s)²)),             (24)

 

 

    Если же радиоволна приходит в горизонтальной (угломестной) плоскости, то нельзя рассматривать условие нормального падения, так как волна приходит под некоторым углом j. В этом случае разность хода ΔΥ₁ к разнесенным на базу d антеннам отличается от ΔΥ на расстояние, равное

 

d’=d·cos j,                            (25)

 

    Отсюда выражение для расчета величины среднеквадратической погрешности определения угла места (s(j)_a) имеет вид:

 

s²(j)_a =arctg(2s_j²)/(k²×d²cosj²)×(1- exp(-s_j²×(d×cosj/L_s)²)),                    (26)

 

    Достоверность полученных выражений (24, 26) подтверждается сведением в частных случаях при d << R(d), d >> R(d) к известным (3, 4) и совпадением полученных аналитических зависимостей с результатами экспериментальных исследований.

 

2. обсуждение полученных результатов

 

    Полученные зависимости (24, 26) позволяют количественно оценить влияние степени возмущения ионосферы, определяемой величиной s_j² (14), на точность определения координат источника радиоизлучения в тангенциальном (s²(Q)_a) и радиальном (s²(j)_a) направлениях. При этом в рассмотрении принято допущение, что отношение сигнал/шум значительно больше 5 и не влияет на точность определения углов прихода волны при измерении интерферометром [1]. Выражения (14, 15) показывают существенную зависимость s²(Q)_a и s²(j)_a от физических параметров ионосферы (N(h), b, L_s) и выбора рабочей частоты.

В таблице 1 представлены результаты расчета указанных коэффициентов (14, 15, 24, 26) при заданных параметрах ионосферы и рабочей частоте радиолинии (f_o). Отметим, что значения указанных параметров находятся в пределах области допустимых значений.

 

Таблица 1

 

Примечание. d=300 м, s_и=0,007 рад., s_ш=0,018 рад., s_hд=1,48×10^-5 рад., D=1000 км.

 

    Анализируя результаты, приведенные в таблице 1, можно сделать вывод, что изменение параметров ионосферы (N(h), b, L_s), а, следовательно, и s_j², существенно влияет на погрешность определения углов прихода волы (s(Q)_a², s(j)_a²) при измерениях интерферометром.

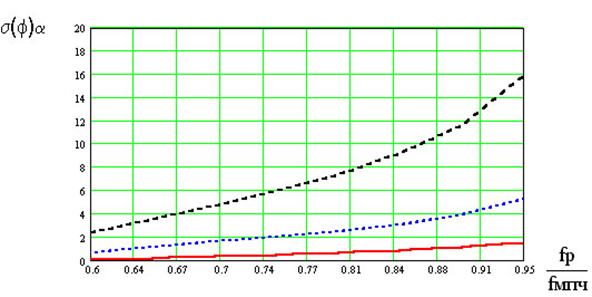
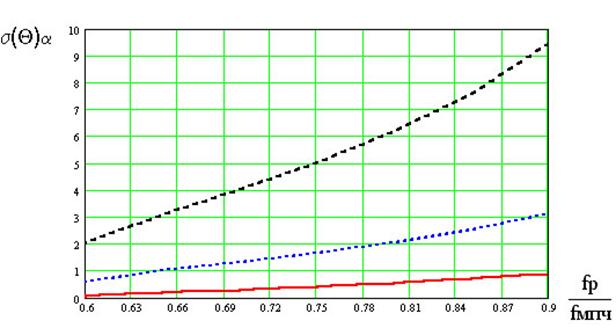
    В соответствии с таблицей 1 и выражениями (24, 26) были построены кривые (рис. 2, 3) зависимости погрешностей определения углов прихода волны в тангенциальном (s²(Q)_a) и радиальном (s²(j)_a) направлениях от рабочей частоты радиолинии, при разных значениях s²_j, выраженной через N(h), b, L_s.

 

Рис. 2. Зависимость величины среднеквадратической погрешности определения углов прихода радиоволны в тангенциальном направлении при различных состояниях ионосферы от отношения f_o/f_МПЧ

 

 

Рис. 3. Зависимость величины среднеквадратической погрешности определения координат источника радиоизлучения в радиальном направлении при различных состояниях от отношения f_o/f_МПЧ

 

    Анализируя рис. 2, 3 можно сделать следующий выводы:

 приближение рабочей частоты к максимально применимой частоте приводит к тому, что погрешности s²(Q)_a и s²(j)_a  обусловленные рассеиванием радиоволн на неоднородностях ионосферы могут существенно превышать погрешности s_и, s_ш, s_hд;

погрешность определения углов прихода волны в радиальном направлении выше, чем в тангенциальном.

 

3. ВЫВОДЫ:

 

    По результатам проведенных исследований можно сделать следующие выводы:

полученные аналитические выражения (24, 26) позволяют количественно оценить погрешность определения углов прихода волны при измерении интерферометром в радиальном и тангенциальном направлении для всех случаев, при d << R(d), d >> R(d) и d »R(d);

применение полученных выражений (14, 15) с учетом параметров среды распространения радиоволн позволит повысить объективность в оценки точности определения углов прихода волны и соответственно координат источника радиоизлучения в условиях нормальной и  возмущенной ионосферы при измерениях интерферометром.

 

СПИСОК ЛИТЕРАТУРЫ

1. Беляевский Л.С., Черкашин В.Г. Точность радиоэлектронных измерительных систем. – К.: Технiка, 1981. – 136 с.

2. Рабинович С.Г. Погрешности измерений. - Л.: Энергия, 1978.–286 с.

3. Стейн С., Джонс Дж. Принципы современной теории связи и их применение к передаче дискретных сообщений. - М.: Связь, 1971. - 376 с.

4. Пашинцев В.П., Колосов Л.В., Тишкин С.А., Антонов В.В. Применение теории фазового экрана для разработки модели односкачкового декаметрового канала связи.//Радиоэлектроника и электроника, 1996.т.41, №1. с.21 - 26.

5. Колосов М. А., Арманд Н. А., Яковлев О. И. Распространение радиоволн при космической связи. - М.: Связь, 1969, - 155 с.

6. Лобкова Л. М. Распространение радиоволн над морской поверхностью. - М.: Радио и связь, 1991. - 256 с.

7. Смирнов А.А. Физика процесса и статистические  характеристики подрелеевских замираний в декаметровых каналах связи // Информационные системы на железнодорожном транспорте. Украинская академия наук. №6, 1998. – с. 29-30.

8. Дэвис К. Радиоволны в ионосфере. - М.: Мир, 1973. - 502 с.

9. Калинин А. И., Черенкова Е. Л. Распространение радиоволн и работа радиолиний. - М.: Связь, 1971. - 440 с.

 

---

Авторы:
Копытов Владимир Вячеславович, ктн,СНС, e-mail: rosenko@stavsu.ru

Пикалов Олег Геннадиевич,

филиал Ростовского военного института РВ, г. Ставрополь.

 

оглавление

дискуссия