The generalized likelihood ratio (GLR) method uses a
likelihood ratio
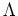
as a test-statistic, in which all
unknown parameters of a signal and noise are substituted by
them ML-estimates. In general, obtained test-statistic
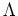
has a complicate probability distribution. This does not
allow to find analytically the test-statistic threshold
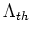
for the given constant level of false alarm
probability
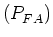
. Therefore, various numerical or
asymptotic methods can be adopted. Unfortunately such
methods perform well only when the number of collected
samples is large, hereafter referred as
large sample
case. In the present work the constant-false-alarm-rate
(CFAR) detection task of multidimensional Gaussian complex
signals with unknown spatial covariance matrix on a
background of additive Gaussian complex noise of a unknown
power is solved for the case where only few samples are
collected, hereafter referred as
small sample case.
In spite of the fact that the distribution function of the
random variable
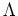
is not represented in an analytical
form, the exact analytical expressions for statistical
moments of any order for the function
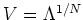
were
found. On the next step the approximating series for
probability density function (PDF)of the random variable
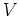
was constructed with the help of the beta probability
distribution and orthogonal Jacobi polynomials on the base
of known test-statistic
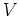
higher orders moments. The
accuracy of the test-statistic
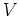
cumulative distribution
function (CDF) approximation and the accuracy of threshold
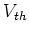
calculations on the given
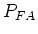
for various
numbers of approximating series terms were checked by
simulation. It is shown, that the employed approximating
series has very high rate of convergence.