

Next: Problem Formulation
Up: Approximation of distribution function
Previous: Approximation of distribution function
The generalized likelihood ratio (GLR) test is widely used
for a solution of a detection task of signals with unknown
statistical characteristics in case of noise present with
unknown parameters too. The GLR- method uses a likelihood
ratio as a test-statistic, in which all unknown parameters
of a signal and noise are substituted by them
maximum-likelihood (ML) estimates obtained from
samples [1]. For example, in the case of signal
propagation in random inhomogeneous channel there is a
problem of a detection of a useful signal with an unknown
wavefront and/or incomplete spatial coherence on the
background of an additive noise with unknown
intensity [2,3]. However, in general (for
any sample size) the GLR test-statistic has complicate
probability density function (PDF) and cumulative
distribution function (CDF). The last fact does not allow to
analytically find the test-statistic threshold values for a
given constant level of a false alarm probability 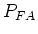 (in accordance with Neyman-Pearson criterion). Therefore,
for threshold calculation various numerical methods or
asymptotic analytical methods good for large-sample tests
only are used. In the present work a new method for the
analytical calculation of the threshold for a given constant
false alarm probability level in the case of small-sample
test-statistic is described. Accuracy of the threshold
evaluation by this method is investigated on the example of
detection of complex multi-dimensional Gaussian signals with
an a-priori unknown spatial covariance matrix on
the background of complex additive spatially white noise
with unknown power.
(in accordance with Neyman-Pearson criterion). Therefore,
for threshold calculation various numerical methods or
asymptotic analytical methods good for large-sample tests
only are used. In the present work a new method for the
analytical calculation of the threshold for a given constant
false alarm probability level in the case of small-sample
test-statistic is described. Accuracy of the threshold
evaluation by this method is investigated on the example of
detection of complex multi-dimensional Gaussian signals with
an a-priori unknown spatial covariance matrix on
the background of complex additive spatially white noise
with unknown power.



Next: Problem Formulation
Up: Approximation of distribution function
Previous: Approximation of distribution function