|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 12, 2002 |
|
Моделирование процессов дискретного взаимодействия в ЛБВ с резонаторными замедляющими системами.
Мухин С.В.; e-mail: rt@miem.edu.ru
Московский государственный институт электроники и математики
(технический университет).
Получена 7 декабря 2003 г.
Осуществлен электродинамически обоснованный выбор модели резонаторных замедляющих систем, одинаково пригодной для описания электродинамических характеристик и возбуждения заданным током. Рассмотрены настраиваемые модели оконечных устройств секции ЛБВ с дискретным взаимодействием. Выбрана система нелинейных уравнений ЛБВ с дискретным взаимодействием, объединяющая разработанные модели в макромодель прибора.
-
Моделирование резонаторных замедляющих систем, возбуждаемых током.
-
Моделирование оконечных устройств секций ЛБВ на основе резонаторных замедляющих систем.
СВЧ устройства средней и большой мощности, предназначенные для усиления и генерации электромагнитных колебаний, базируются на использовании электровакуумных приборов (ЭВП) СВЧ разнообразных типов и, в частности, ламп бегущей волны с дискретным взаимодействием на основе резонаторных замедляющих систем. Исследование и разработка таких приборов представляет собой важное направление науки и техники, в развитии которого сегодня остро нуждаются как оборонные, так и многие гражданские отрасли.
Новые требования, предъявляемые к этим приборам СВЧ, предусматривают укорочение длины волны, увеличение мощности и кпд, расширение рабочей полосы частот, что приводит к необходимости создания новых средств их проектирования и создания новых принципов их построения.
Ввиду сложности ЛБВ, включающих электродинамические системы, электронно-оптические системы, коллекторы, пространство взаимодействия электронов с полем, всевозрастающую роль при их проектировании получают анализ, моделирование и проектирование приборов на ЭВМ, которые стали сейчас необходимым инструментом разработок.
В последних публикациях, в частности в материалах конференций по вакуумной электронике (2000 г. – США, Монтерей, 2001 г. – Голландия, 2002 г.- США, Монтерей), содержатся сведения о большом числе новых программных комплексов для моделирования и проектирования ЭВП СВЧ и их узлов.
Для моделирования процессов в ЭВП СВЧ разработан ряд программных комплексов, опирающихся на прямое численное решение уравнений Максвелла и уравнений движения электронов, анализирующих прибор в комплексе с использованием новых возможностей вычислительной техники по быстродействию и объему памяти. К ним можно отнести программы «Карат», MAFIA 3D, MAGIC 3D и другие. Такие программы дают возможность детального анализа микропроцессов взаимодействия электронных пучков с полем, однако требуют большого времени расчета даже для простых конфигураций электродинамических систем, что ограничивает их возможности при проектировании ЭВП СВЧ с реальными замедляющими системами.
Поэтому важнейшим направлением создания методов и программных комплексов для моделирования и проектирования ЭВП СВЧ остается теория возбуждения электродинамических систем, использование моделей электронных пучков и электродинамических систем, дающих возможность достаточно быстрого анализа и проектирования приборов.
Новые возможности для проектирования и разработки приборов открываются при создании методов расчета и программ для комплексного анализа процессов нелинейного взаимодействия электронов с электромагнитным полем в сочетании с расчетом электродинамических систем, определяющих характеристики этого поля. Такой подход дает возможность моделирования и проектирования приборов от геометрии замедляющих систем до выходных высокочастотных характеристик в едином цикле, создает основу для интерактивного проектирования и создания приборов с качественно новыми характеристиками.
Для развития этого направления необходимо решение следующих задач:
- Разработка моделей резонаторных замедляющих систем, возбуждаемых заданным током, адекватно описывающих их электродинамические характеристики и процессы дискретного взаимодействия электронов и поля в них, позволяющих строить на их основе макромодели приборов.
- Разработка моделей оконечных устройств, легко встраиваемых в макромодель прибора и адекватно описывающих согласование секций прибора.
§ Разработка алгоритма комплексного исследования процессов дискретного взаимодействия электронов с электромагнитным полем и характеристик резонаторных замедляющих систем.
В данной работе рассмотрены подходы к решению этих задач.
2. Моделирование резонаторных замедляющих систем, возбуждаемых током.
Особенности взаимодействия электронов и поля в ЛБВ с резонаторными замедляющими системами определяются характером распределения полей в такой системе. Поскольку амплитуды полей вдоль резонаторной замедляющей системы изменяются от максимального значения в зазоре взаимодействия до минимального в пролетном канале, взаимодействие электронного пучка с полем происходит дискретно в ограниченных областях. Наиболее общим при решении задач данного типа является дискретный подход.
Анализ методов решения задачи дискретного взаимодействия в ЛБВ с резонаторными замедляющими системами [1-7] показывает многообразие форм уравнений возбуждения. Они сформулированы в двух формах дифференциальной и интегральной. Интегральная форма может быть получена независимо либо из дифференциальной формы уравнения возбуждения. При дискретном подходе аналогом дифференциальной формы является разностная форма уравнений возбуждения, а интегральной - форма в виде конечного ряда. Исследования, проведенные в работе [8], показали, что с помощью формальных преобразований известные уравнения возбуждения сводятся к конечно-разностным уравнениям двух типов:
Коэффициенты этих уравнений могут быть выражены через коэффициенты матрицы передачи шестиполюсника, моделирующего ячейку резонаторной ЗС, возбуждаемую током, как это сделано в (1,2), элементы эквивалентной схемы ячейки или электродинамические характеристики ЗС, в случае использования полевых методов. Обосновать использование той или иной математической модели, при описании дискретного взаимодействия, позволяет разностная форма электродинамической теории возбуждения [9].
Согласно этой теории возбуждения, суммарное поле разностное уравнение для полного поля Е, возбуждаемого произвольным током имеет вид
Правая часть уравнения определяется возбуждающим током и имеет вид
![]() ,
,
где ![]() ,
,

![]() - объемы одного периода системы, причём
- объемы одного периода системы, причём ![]() - объём справа,
- объём справа, ![]() - слева от данного
сечения
- слева от данного
сечения ![]() ..
..
Разностное уравнение (3) является точным следствием обычных формул возбуждения и справедливо при произвольном выборе сечения z. При решении уравнения (3) для конечного отрезка системы краевые условия накладываются на Е и DE или их комбинации на одной или двух границах отрезка.
В предположении постоянства фазы в зазоре взаимодействия и при проведении усреднения поля по сечению пучка (одномерная теория) интегралы по k-1 и k+1 зазорам в правой части разностного уравнения возбуждения обращаются в ноль, и в уравнении для k-го зазора остается только ток данного зазора
Это уравнение можно переписать также относительно потенциала на зазоре
Нетрудно видеть, что оно совпадает по форме с уравнением (2).
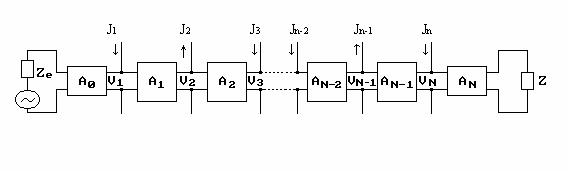
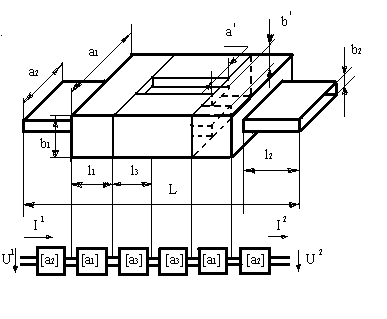
Таким образом, для описания ЛБВ с дискретным взаимодействием, в которых фаза поля в зазорах взаимодействия в продольном направлении остается постоянной, электродинамически обоснованным является использование разностного уравнения (2). Этому уравнению соответствует шестиполюсник, у которого входы возбуждения полем и током объединены. Секция ЛБВ, возбуждаемая заданным током, в этом случае моделируется цепочкой таких шестиполюсников (рис.1), что позволяет легко учитывать граничные условия на концах секции и отражения, возникающие при объединении в секцию неидентичных ячеек.
Рис.1. Модель секции ЛБВ, составленная из шестиполюсников.
Адекватность математической модели дискретного взаимодействия определяется точностью задания коэффициентов конечно – разностного уравнения, имеющих определенный электродинамический смысл (5) и определяемых через коэффициенты матрицы передачи четырехполюсника, который получается из шестиполюсника в отсутствии возбуждающего тока. Этот четырехполюсник, в свою очередь является математической моделью ячейки резонаторной ЗС. Его коэффициенты определяют точность восстановления электродинамических характеристик моделируемой резонаторной замедляющей системы. Таким образом, их правильный выбор обеспечивает одновременно адекватное описание процессов дискретного взаимодействия в ЛБВ и электродинамических процессов в замедляющей системе.
Коэффициенты матрицы передачи этого четырехполюсника могут быть определены в результате решения внутренней электродинамической задачи или при использовании эквивалентных схем. Точные электродинамические методы не применимы из-за больших затрат вычислительных ресурсов, которые возрастают еще больше при решении задачи дискретного взаимодействия. Известная эквивалентная схема для данного типа шестиполюсника [10] требует для своего построения предварительных экспериментальных исследований в каждом конкретном случае и не обеспечивает необходимой точности во всей полосе пропускания. Поэтому целесообразно использовать модели резонаторных замедляющих систем, построенные методом эквивалентных систем [11].
Метод эквивалентных систем является разновидностью метода частичных областей и позволяет строить простые модели резонаторных ЗС, описывающие их электродинамические характеристики с требуемой точностью. Вместо того чтобы анализировать процессы в исходной ЗС, имеющей сложную конфигурацию границ, производится её замена на эквивалентную систему с аналогичными свойствами, построение модели которой методом частичных областей упрощается.
При построении
эквивалентной системы исходная замедляющая система разбивается на частичные
области плоскостями перпендикулярными направлению распространения СВЧ энергии в
ней. Выделенные частичные области заменяются волноведущими каналами с
конфигурацией границ, для которой известно аналитическое решение внутренней
электродинамической задачи. В результате получается эквивалентная замедляющая
система. Для описания частичных областей этой системы вводятся эквивалентные ![]() , что позволяет перейти
при их описании к эквивалентным линиям передачи - базовым элементам и
единообразно описать их матрицами передачи четырехполюсников.
, что позволяет перейти
при их описании к эквивалентным линиям передачи - базовым элементам и
единообразно описать их матрицами передачи четырехполюсников.
На основе анализа условий сшивания полей на границах частичных областей проводится соединение четырехполюсников в эквивалентную схему ячейки анализируемой замедляющей системы и определяется ее суммарная матрица передачи. Разным типам замедляющих систем соответствуют разные схемы соединения базовых элементов. Поскольку при этом используются одни и те же базовые элементы, процесс построения модели унифицируется.
Идентичность свойств исходной и эквивалентной замедляющих систем обеспечивается подбором размеров эквивалентной ЗС.
В случае, когда границы реальной и эквивалентной ЗС совпадают, при описании базовых элементов используются размеры реальной ЗС.
Если границы не совпадают, для определения размеров эквивалентной системы используются разные подходы:
- приближенные соотношения, связывающие размеры реальной и эквивалентной замедляющих систем [12];
- определение размеров эквивалентной системы в результате параметрической оптимизации по опорным точкам, полученным в результате натурного или численного эксперимента [13];
- использование регрессионных зависимостей, связывающих размеры эквивалентной и реальной замедляющих систем [14].
Построение эквивалентной системы рассмотрим на примере ЗС типа ЦСР со щелями связи, повернутыми на 1800, представленной на рис.2.
Рис.2. Замедляющая система типа ЦСР со щелями связи повернутыми на 1800.
Эта ЗС имеет сложную аксиально-симметричную конфигурацию, однако, если предположить отсутствие связи между резонаторами через пролетные каналы, распространение СВЧ энергии в ней осуществляется по пути, выделенному сплошной линией на рис.2.
Плоскостями перпендикулярными направлению распространения СВЧ энергии выделяются частичные области: область щели связи (2); область центральной части резонатора (3); периферийная область резонатора (1) (рис.2.). Области, выделенные в резонаторе, имеют прямоугольное и Н-образное поперечные сечения, размеры которых меняются по длине. Каждой выделенной области ставится в соответствие регулярный волноведущий канал с простой конфигурацией границ, не совпадающей с границами ячейки. Ячейке аксиально-симметричной ЗС (рис.2) ставится в соответствие эквивалентная ЗС, составленная из отрезков прямоугольных и Ш-образного волноводов (рис.3), для которых известно решение внутренней задачи электродинамики.
Рис.3. Эквивалентная замедляющая система, составленная из отрезков прямоугольных волноводов.
Исключая из рассмотрения влияние изгибов, то есть, не учитывая высшие типы волн, получают линейную эквивалентную систему, представленную на рис.4.
Рис.4. Волноводно-резонаторная модель ячейки ЦСР.
Выделенные
волноведущие каналы, в соответствии с методом эквивалентных систем, заменяются
эквивалентными линиями передачи с ![]() для волны Н10,
распространяющейся в них. Каждый волноведущий канал описывается своей
матрицей передачи
для волны Н10,
распространяющейся в них. Каждый волноведущий канал описывается своей
матрицей передачи ![]() , и линейная эквивалентная система
представляется в виде каскадного соединения четырехполюсников - эта модель
получила название волноводно-резонаторная модель (ВРМ). ВРМ ячейки ЗС типа ЦСР
представлена на рис.4. Суммарная матрица передачи
, и линейная эквивалентная система
представляется в виде каскадного соединения четырехполюсников - эта модель
получила название волноводно-резонаторная модель (ВРМ). ВРМ ячейки ЗС типа ЦСР
представлена на рис.4. Суммарная матрица передачи ![]() , связывающая эквивалентные токи и
напряжения на входе и выходе ВРМ, определяется перемножением матриц передач
отдельных участков
, связывающая эквивалентные токи и
напряжения на входе и выходе ВРМ, определяется перемножением матриц передач
отдельных участков ![]()
Через элементы этой матрицы передачи определяются дисперсия и сопротивление связи рассматриваемой замедляющей системы, и она является основой модели ячейки ЦСР, возбуждаемой током.
Дисперсия моделируемой ЗС типа ЦСР определяется по формуле
в которой учитывается геометрический поворот вектора напряженности электрического поля от ячейки к ячейке добавлением p. В выражении (7):
![]() - набег фазы р-ой гармоники на период D реальной ЗС;
- набег фазы р-ой гармоники на период D реальной ЗС;
![]() - набег фазы волны, распространяющейся по
ячейке эквивалентной линейной ЗС с периодом
- набег фазы волны, распространяющейся по
ячейке эквивалентной линейной ЗС с периодом ![]() ;
;
p=0,±1,±2....
Дисперсионное
уравнение относительно ![]() имеет следующий вид
имеет следующий вид
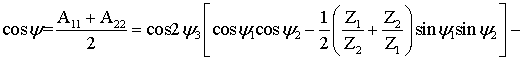
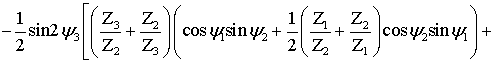
Для
определения сопротивления связи рассматривается возбуждение ВРМ заданным током
- ![]() , включенным
на отрезке Н-образного волновода (рис.5).
, включенным
на отрезке Н-образного волновода (рис.5).
Рис.5. Возбуждение
ячейки ЦСР заданным током ![]() .
.
Выделение
ячейки эквивалентной ЗС осуществляется так, чтобы возбуждающий источник тока
оказался включенным на ее входе. ![]() и
и ![]() - входные импедансы отброшенных частей
эквивалентной системы. Для бесконечной системы
- входные импедансы отброшенных частей
эквивалентной системы. Для бесконечной системы ![]() .
.
Входная проводимость в точке включения источника тока определяется соотношением:
где ![]() - характеристические входные
сопротивления, пересчитанные слева и справа к точке возбуждения
- характеристические входные
сопротивления, пересчитанные слева и справа к точке возбуждения ![]() .
.
Величины ![]() определяются из
уравнения
определяются из
уравнения
где ![]() - элементы суммарной матрицы передачи для
трех базовых элементов (рис.5), с "+" посчитанные справа к точке
- элементы суммарной матрицы передачи для
трех базовых элементов (рис.5), с "+" посчитанные справа к точке ![]() , с "-" слева
к точке
, с "-" слева
к точке ![]() при
нагрузках на концах, соответственно
при
нагрузках на концах, соответственно ![]() и
и ![]() .
.
Окончательно
входная проводимость в точке ![]() определяется выражением
определяется выражением

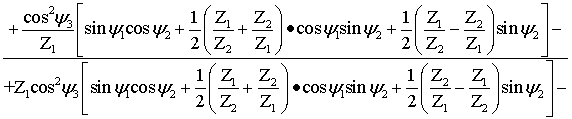
С учетом того,
что напряжение на зазоре ![]() , а мощность волны, бегущей от точки
возбуждения
, а мощность волны, бегущей от точки
возбуждения ![]() ,
,
![]() сопротивление
связи
сопротивление
связи
где ![]() - амплитуда поля в зазоре,
- амплитуда поля в зазоре,
![]() - коэффициент формы зазора.
- коэффициент формы зазора.
В рассматриваемой модели наличие потерь может быть учтено введением постоянной затухания для каждого волноведущего канала составляющего ВРМ.
Как показали исследования, построенная таким образом модель ЗС типа ЦСР правильно отражает электродинамические процессы, происходящие в ней. Количественное соответствие достигается выбором размеров эквивалентной системы. При использовании приближенных соотношений, связывающих размеры реальной и эквивалентной замедляющих систем, соответствие достигается при изменении размеров в следующих пределах:
![]() ,
, ![]() ,
, ![]() ,
,  ,
,
![]()
При использовании для настройки модели опорных точек область ее адекватности существенно расширяется
![]()
![]()
![]()
Максимальная относительная погрешность расчета коэффициента замедления составляет 1%, сопротивления связи - 5%. На рис.6 проведено сравнение рассчитанных и экспериментальных электродинамических характеристик.
Рис.6. Сравнение
экспериментальных ![]() и
рассчитанных электродинамических характеристик для ЗС типа ЦСР при настройке
всех десяти (сплошная линия), или четырех (пунктир) параметров ВРМ по четырем
опорным точкам.
и
рассчитанных электродинамических характеристик для ЗС типа ЦСР при настройке
всех десяти (сплошная линия), или четырех (пунктир) параметров ВРМ по четырем
опорным точкам.
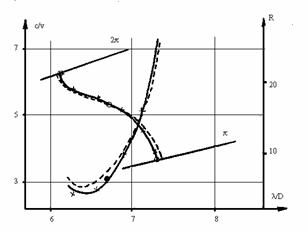
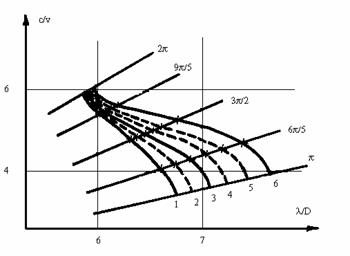
Использование регрессионных зависимостей, связывающих размеры реальной и эквивалентной ЗС, позволяет с высокой точностью рассчитывать ее электродинамические характеристики при изменении размеров в области, для которой построены регрессионные зависимости. На рис.7 проведено сравнение рассчитанных и экспериментальных характеристик в этом случае.
Рис.7.Экспериментальные
![]() и
рассчитанные по ВРМ, с привлечением регрессионной модели (сплошная линия),
электродинамические характеристики ЗС типа ЦСР при изменении угла раскрыва
щели связи. Дисперсионные характеристики, по которым строилась регрессионная
модель, отмечены пунктиром.
и
рассчитанные по ВРМ, с привлечением регрессионной модели (сплошная линия),
электродинамические характеристики ЗС типа ЦСР при изменении угла раскрыва
щели связи. Дисперсионные характеристики, по которым строилась регрессионная
модель, отмечены пунктиром.
Высокая точность восстановления дисперсионных характеристик обеспечивается точностью определения коэффициентов матрицы передачи, моделирующей ячейку замедляющей системы. Это в свою очередь обеспечивает адекватность модели дискретного взаимодействия.
С помощью метода эквивалентных систем могут быть построены модели разных резонаторных систем, в частности прямоугольной формы, которые используются в ЛБВ миллиметрового диапазона.
3. Моделирование оконечных устройств секций ЛБВ на основе резонаторных замедляющих систем.
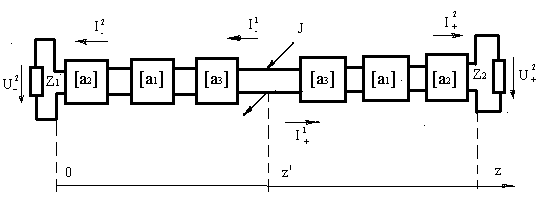
Как показано
выше, секция ЛБВ на основе резонаторных замедляющих систем моделируется
цепочкой шестиполюсников, оканчивающейся с двух сторон некоторыми
"обобщенными" оконечными устройствами (рис.1). В качестве модели
такого устройства используется фазовращающий четырехполюсник с характеристическим
сопротивлением, равным входному сопротивлению полубесконечной ЗС в точке его
подключения, и частотно-зависимым фазовым сдвигом ![]() , нагруженный сопротивлением
, нагруженный сопротивлением ![]() . Модели оконечных
устройств одной секции характеризуются на каждой частоте четырьмя параметрами:
. Модели оконечных
устройств одной секции характеризуются на каждой частоте четырьмя параметрами:
![]() .
.
Вид модели оконечного устройства определяется способом задания частотных зависимостей этих параметров. Возможны два подхода к построению модели.
При первом
подходе сопротивления ![]() и
и
![]() считаются
постоянными во всём частотном диапазоне. Фазовращающие четырехполюсники
описываются матрицей передачи, коэффициенты которой определяют частотную
зависимость фазового сдвига
считаются
постоянными во всём частотном диапазоне. Фазовращающие четырехполюсники
описываются матрицей передачи, коэффициенты которой определяют частотную
зависимость фазового сдвига ![]() . При построении матрицы передачи
фазовращателя, используется постоянная распространения
. При построении матрицы передачи
фазовращателя, используется постоянная распространения ![]() и характеристическое
сопротивление
и характеристическое
сопротивление ![]() четырехполюсников,
описывающих ячейки резонаторной замедляющей системы
четырехполюсников,
описывающих ячейки резонаторной замедляющей системы
Фазовый сдвиг
на оконечном устройстве определяется частотной зависимостью постоянной
распространения ![]() и
параметром
и
параметром ![]() .
Этот параметр позволяет непрерывно менять число ячеек в эквивалентной схеме
секции прибора и, тем самым, смещать минимумы и максимумы
.
Этот параметр позволяет непрерывно менять число ячеек в эквивалентной схеме
секции прибора и, тем самым, смещать минимумы и максимумы ![]() в широких пределах, изменять их
число в полосе прозрачности ЗС. Модели оконечных устройств секции прибора в
этом случае описываются независимыми от частоты параметрами
в широких пределах, изменять их
число в полосе прозрачности ЗС. Модели оконечных устройств секции прибора в
этом случае описываются независимыми от частоты параметрами ![]() . Для определения этих параметров
используется процедура оптимизации. Для повышения точности модели в каждое
оконечное устройство может быть введён дополнительный отрезок линии с тем же
значением
. Для определения этих параметров
используется процедура оптимизации. Для повышения точности модели в каждое
оконечное устройство может быть введён дополнительный отрезок линии с тем же
значением ![]() , но
другим характеристическим сопротивлением:
, но
другим характеристическим сопротивлением: ![]() . В этом случае
оптимизация идет уже по восьми параметрам. Результаты моделирования оконечных
устройств в этом случае приведены на рис.8.
. В этом случае
оптимизация идет уже по восьми параметрам. Результаты моделирования оконечных
устройств в этом случае приведены на рис.8.
Рис.8. Модуль
коэффициента отражения на входе в секцию. Расчет (сплошная линия), эксперимент ![]() .
.
Наличие большого числа локальных минимумов в этом случае затрудняет оптимизацию, поэтому была разработана вторая модель, не требующая оптимизации.
Частоты,
соответствующие минимумам и максимумам на кривой ![]() , характеризуются тем, что на этих частотах
набег фазы волны на всей цепочке имеет величину, кратную
, характеризуются тем, что на этих частотах
набег фазы волны на всей цепочке имеет величину, кратную ![]() .
.
где ![]() - частота i -го
минимума
- частота i -го
минимума ![]() ;
;
![]() - частота j -го
максимума
- частота j -го
максимума ![]() ;
;
N - число ячеек в секции;
![]() - набег фазы на одной ячейке ЗС (ячейки
могут быть неидентичными).
- набег фазы на одной ячейке ЗС (ячейки
могут быть неидентичными).
Из (14) видно,
что, рассчитав 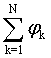 для
всех
для
всех ![]() , можно
получить для этих частот величины
, можно
получить для этих частот величины ![]() , задав только одно значение n для какой-либо из частот
, задав только одно значение n для какой-либо из частот![]() .
.
Выбрав одну из
частот ![]() ,
рассчитывается
,
рассчитывается ![]()
 и выбирается
минимальное n из условии
и выбирается
минимальное n из условии ![]() . Тогда сумма
. Тогда сумма ![]() будет иметь положительное
минимальное значение, и для любой
будет иметь положительное
минимальное значение, и для любой ![]() её можно рассчитать по формулам:
её можно рассчитать по формулам:
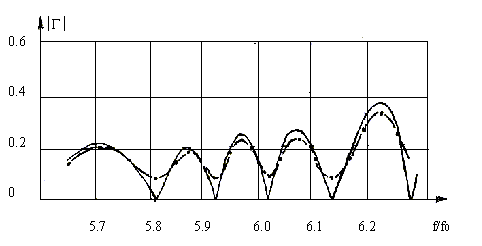
Таким образом, получается ряд
значений суммарного набега фазы ![]() на частотах
на частотах ![]() ,
, ![]() , который расставляет минимумы и максимумы
, который расставляет минимумы и максимумы ![]() на нужные места.
на нужные места.
Для того чтобы
получить ![]() в
промежуточных точках, достаточно построить кубический сплайн по значениям
в
промежуточных точках, достаточно построить кубический сплайн по значениям ![]() на частотах
на частотах ![]() ,
, ![]() . Конкретные значения
. Конкретные значения ![]() и
и ![]() для заданной на каждой частоте
суммы
для заданной на каждой частоте
суммы ![]() невозможно
определить, имея только одну экспериментальную кривую
невозможно
определить, имея только одну экспериментальную кривую ![]() , так как её вид зависит от
, так как её вид зависит от ![]() . В качестве первого
приближения принимается
. В качестве первого
приближения принимается ![]() .
.
Сопротивления
нагрузок в точках максимумов ![]() можно вычислить, решив для каждой
можно вычислить, решив для каждой ![]() нелинейное уравнение
нелинейное уравнение
В этом уравнении два неизвестных
- ![]() и
и ![]() .
.
Если принять
условие ![]() ,
которое определяет нулевые значения
,
которое определяет нулевые значения ![]() в минимумах, уравнение (10) будет иметь
два решения на каждой
в минимумах, уравнение (10) будет иметь
два решения на каждой ![]()
![]() .
.
Выбор одного из этих значений не
влияет на вид расчётной кривой ![]() , поэтому при наличии только одной
экспериментальной характеристики в этом вопросе остаётся произвол. В первом
приближении выбирается
, поэтому при наличии только одной
экспериментальной характеристики в этом вопросе остаётся произвол. В первом
приближении выбирается ![]() во всём рабочем диапазоне прибора. Также
как для фазового набега
во всём рабочем диапазоне прибора. Также
как для фазового набега ![]() , для сопротивления нагрузок строится
сплайн, чтобы иметь возможность определять
, для сопротивления нагрузок строится
сплайн, чтобы иметь возможность определять ![]()
![]() в промежуточных точках.
в промежуточных точках.
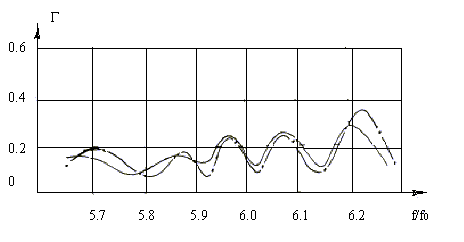
Полученные таким образом зависимости позволяют определить параметры фазовращающего четырехполюсника и величину нагрузки на нужной частоте. Результаты моделирования оконечных устройств в этом случае приведены на рис.9.
Рис.9. Модуль коэффициента
отражения на входе секции. Расчет по модели на сплайн интерполяции (сплошная
линия), эксперимент ![]() .
.
4. Модель дискретного взаимодействия электронов с электромагнитным полем в ЛБВ на основе резонаторных замедляющих систем.
Как показано выше секция ЛБВ возбуждаемая током, моделируется цепочкой шестиполюсников (рис.1), что позволяет легко учитывать граничные условия на концах секции и отражения, возникающие при объединении в секцию неидентичных ячеек.
В приближении постоянства фазы в зазоре взаимодействия разностное уравнение возбуждения для k-го зазора взаимодействия включает лишь ток, возбуждающий данный зазор. Отсюда следует, что токи, возбуждающие цепочку резонаторов, действуют независимо и при записи уравнений возбуждения можно воспользоваться принципом суперпозиции. При этом уравнение возбуждения цепочки шестиполюсников входным сигналом и заданным током записывается в виде ряда, известного из [15].
где ![]() - число зазоров взаимодействия
- число зазоров взаимодействия
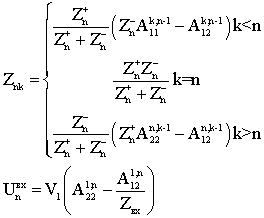
Продольная компонента поля пространственного заряда определяется через коэффициент депрессии и гармоники тока. Чтобы получить возможность численного решения уравнений используется метод “крупных частиц”. В качестве крупной частицы рассматривается жесткий диск, внутри которого все электроны движутся с одинаковой скорость в направлении оси z , то есть предполагается, что пульсации пучка отсутствуют. Центр масс подобной частицы располагается на оси системы, поэтому в уравнение движения входит только z- компонента силы действующей на нее.
Исходная система
уравнений взаимодействия приводится к безразмерному виду путем введения
нормированной энергии электрона, нормированных координаты и фазы, коэффициентов
возбуждения ![]() ,
нормированных относительно сопротивления свободного пространства. Постоянная
нормировки задается соотношением
,
нормированных относительно сопротивления свободного пространства. Постоянная
нормировки задается соотношением
Использование такой постоянной удобно для описания рассматриваемого здесь дискретного взаимодействия в отличие от параметра усиления C, применяемого для описания взаимодействия в «гладких» ЗС с одной синхронной волной.
Рабочая система уравнений приобретает вид:
где ![]() - напряжение встречного излучения в n-ом зазоре;
- напряжение встречного излучения в n-ом зазоре;
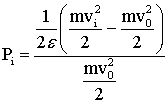 - нормированная энергия электрона;
- нормированная энергия электрона;
![]() - безразмерная длина;
- безразмерная длина;
![]() - фаза i – го
электрона;
- фаза i – го
электрона;
![]()
Это нерелятивистские уравнения, но переменные и параметры в них определяются с учетом релятивистских поправок.
Система уравнений (19) описывает взаимодействие внутри зазора взаимодействия. Между зазорами пучок движется в пролетных трубах, где его формирование осуществляется под действием сил пространственного заряда. Для этих участков система уравнений видоизменяется, в уравнение движения входит только продольная компонента силы пространственного заряда.
Полученная самосогласованная система уравнений моделирует процессы дискретного взаимодействия в ЛБВ на основе резонаторных замедляющих систем с идентичными и неидентичными резонаторами, при произвольном согласовании, в произвольной точке частотного диапазона, включая полосу прозрачности с ее границами и вне ее, в линейном и нелинейном режимах работы прибора.
Для получения
самосогласованного решения системы уравнений (19) используется известная
итерационная процедура [15], в процессе которой выбирается комплексная
амплитуда напряжения встречного излучения в первом резонаторе секции прибора ![]()
Система нелинейных уравнений легко объединяется с моделями резонаторных замедляющих систем и оконечных устройств, рассмотренных выше. Для ее решения в процессе итерационной процедуры может быть использован метод Рунге-Кутта 4-го порядка.
В работе сделан электродинамически обоснованный выбор модели ячейки резонаторной замедляющей системы возбуждаемой током в виде шестиполюсника с объединенными входами возбуждения полем и током. Показано, что метод эквивалентных систем позволяет строить модели резонаторных замедляющих в виде четырехполюсников, описывающие с достаточной точностью электродинамические характеристики резонаторных замедляющих систем и являющиеся основой модели ячейки, возбуждаемой током. Представлены настраиваемые модели оконечных устройств секции ЛБВ, легко встраиваемые в макромодель прибора. Осуществлен выбор системы нелинейных уравнений, описывающих дискретное взаимодействие в ЛБВ с резонаторными замедляющими системами, объединяющей разработанные модели.
6.Список использованной литературы.
1. Kino G.S., Hiramatsu Y., Ruetz J.A. Small-signal and large-signal theories for coupled-cavity TWT. //In Pros. 6th Int. conference on MOGA, 1966, Cambridge, England, p.49.
2. Гассанов А.Г., Денисов А.И., Рапопорт Г.И., Чайка В.Е. Теория приборов О-типа из цепочки связанных неидентичных резонаторов. //Изв. Вузов, Сер. Радиоэлектроника, 1974, т. 17, №11, с. 33.
3. Канавец В.И. Кулоновская калибровка потенциалов и уравнения нелинейной теории мощных приборов с электронным пучком.// Вестник МГУ, сер. физ., вып. 2, 1975, с.159.
4. Иванова Н.Н., Наседкин А.А., Петров Д.М. Вопросы расчета ЛБВ на связанных резонаторах.// Тезисы 8-й конференции по СВЧ электронике. Ростов-на-Дону, 1976.
5. Булгакова Л.В., Трубецков Д.И., Фишер В.Л., Шевчик В.Н. Лекции по электронике СВЧ приборов типа О (дискретный подход к описанию взаимодействия электронного потока с ВЧ электромагнитным полем). Из-во Саратовского университета, 1974, с.221.
6. Осин А.В., Солнцев В.А. Программа для расчета взаимодействия в приборах типа О с периодической структурой. // Электронная техника. Сер.1, Электроника СВЧ, 1980, №9, с.69.
7. Кузнецов С.П. Об одной форме уравнений возбуждения периодического волновода. //Радиотехника и электроника, 1980, т.25, №10, с. 419.
8. Мухин С.В., Солнцев В.А. Сравнительный анализ моделей возбуждения приборов О-типа с периодической структурой.//Тезисы докладов Х Всесоюзного семинара «Волновые и колебательные явления в электронных приборах О-типа». Ленинград, 1990, с.99.
9. Солнцев В.А., Мухин С.В. Разностная форма теории возбуждения периодических волноводов. // Радиотехника и электроника, 1991, т.36, №11, с. 2161.
10. Гаврилов М.В., Трубецков Д.И., Фишер В.А. Теория цепочек активных многополюсников с электронным возбуждением (модель взаимодействия электронного пучка с полями связанных резонаторов). Издательство СГУ, 1981, с.173.
11. Мухин С.В., Солнцев В.А., Ломакин О.Е., Глушков А.Р. Разветвленные схемы из четырехполюсников – модели замедляющих систем. //Лекции по электронике СВЧ и радиофизике (8-я зимняя школа-семинар инженеров). Кн. I, из-во Саратовского университета, 1989, с. 69.
12. Мухин С.В., Ломакин О.Е., Солнцев В.А. Волноводно-резонаторная модель замедляющей системы типа цепочка связанных резонаторов.//Радиотехника и электроника, 1988, т. 33, №8, с. 1637.
13. Ломакин О.Е., Мухин С.В., Солнцев В.А. Расчет характеристик цепочки связанных резонаторов при определении параметров волноводно-резонаторной модели методом опорных точек.// Радиотехника и электроника, 1991, т. 36, №2, с. 296.
14. Ломакин О.Е., Мухин С.В., Солнцев В.А. Применение регрессионных зависимостей для определения параметров математических моделей замедляющих систем. //Радиотехника и электроника, 1990, т. 35, №5, с. 1146.
15. Фишер В.Л. Теория возбуждения активных упорядоченных структур и ее применение к анализу колебательных и волновых явлений в цепочках связанных резонаторов с электронным потоком. Диссертация на соискание ученой степени кандидата физико-математических наук, 1983, Саратов.
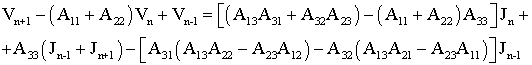 (1)
(1)


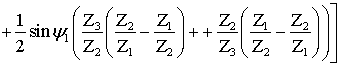
 (11)
(11) ;
; 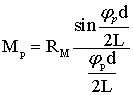 (12)
(12)
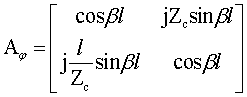 (13)
(13)
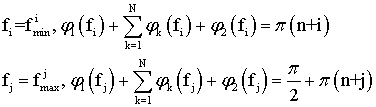 (14)
(14)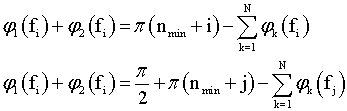 (15)
(15)
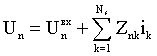 (17)
(17)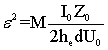 (18)
(18)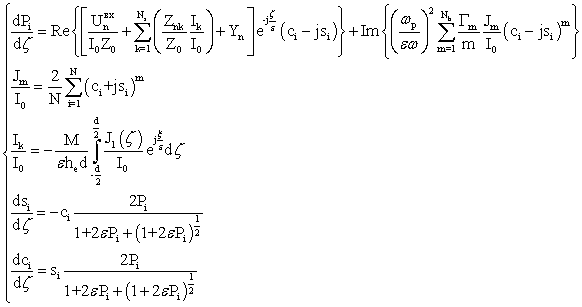 (19)
(19)