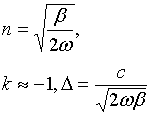|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 12, 2002 |
|
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА РАДИОПРОЗРАЧНОСТИ ТЕПЛОЗАЩИТНЫХ ПОКРЫТИЙ
О.Б. Воробьев, Н. А. Тенякова , e-mail: oleg19640607@mail.ru
Филиал Ростовского Военного Института Ракетных Войск (ФРВИ РВ)
Получена 20 декабря 2002 г.
Рассмотрено влияние поверхностного электрического заряда (ОПЗ) состояний Тамма и Шокли на прохождение радиоизлучения через теплозащитные панели антенн (ТПЗ) космических аппаратов в плотных слоях атмосферы.
В основу метода изучения положена теория Максвелла и классическая теория металлов. Рассмотрена трехслойная модель, описывающая прохождение радиоизлучения через границы плоскослоистой среды: воздух – ОПЗ ТПЗ - ТПЗ, с учетом интерференции излучения, отраженного промежуточными слоями.
Показано существенное влияние поверхностного заряда ТПЗ на прохождение через ТПЗ радиоизлучения.
Теплозащитные покрытия космических аппаратов подвергаются оплавлению под действием плазмы ударной волны, возникающей при их движении в плотных слоях атмосферы [1]. Электромагнитные волны, используемые для радиосвязи с космическими аппаратами, распространяются в слоисто неоднородной среде атмосферного воздуха, плазмы ударно сжатого газа и паров оплавленного слоя, неравномерно нагретого по толщине защитного покрытия.
Если
толщина слоев неоднородной среды мала по сравнению с длиной волны радиосигнала
мы приходим к задаче о распространении электромагнитных волн через совокупность
однородных слоев с разными значениями диэлектрической проницаемости ![]() , магнитной
проницаемости
, магнитной
проницаемости ![]() и
удельной проводимости
и
удельной проводимости ![]() .
Из системы полевых уравнений Максвелла при учете материальных уравнений,
характеризующих свойства среды постоянными величинами макроскопических
параметров
.
Из системы полевых уравнений Максвелла при учете материальных уравнений,
характеризующих свойства среды постоянными величинами макроскопических
параметров ![]() ,
для отдельного слоя получается волновое уравнение вида [2]
,
для отдельного слоя получается волновое уравнение вида [2]
где ![]() - вектор напряженности
электрического поля,
- вектор напряженности
электрического поля, ![]() -
циклическая частота электромагнитной волны,
-
циклическая частота электромагнитной волны, ![]() - скорость света в вакууме.
- скорость света в вакууме. ![]() - оператор Лапласа.
- оператор Лапласа.
Уравнение
Гельмгольца (1) справедливо при условии ![]() , которое выполняется если
максвелловское время релаксации меньше периода электромагнитной волны.
, которое выполняется если
максвелловское время релаксации меньше периода электромагнитной волны.
При учете тормозящих сил, действующих на свободные носители заряда, удельная проводимость среды в поле электромагнитной волны является комплексной величиной [2]
где
![]() - концентрация
свободных носителей заряда,
- концентрация
свободных носителей заряда,
![]() - величина электрического заряда,
- величина электрического заряда, ![]() - эффективная масса
носителя заряда,
- эффективная масса
носителя заряда, ![]() -
коэффициент затухания колебаний.
-
коэффициент затухания колебаний.
Если в соответствии с уравнением (1) ввести комплексную диэлектрическую проницаемость в виде:
то уравнение
(1) будет аналогично волновому уравнению для диэлектрической среды. Мнимая
часть ![]() обусловлена поглощением энергии
электромагнитной волны вблизи резонансных частот, вещественная часть
обусловлена поглощением энергии
электромагнитной волны вблизи резонансных частот, вещественная часть ![]() - омической проводимостью
среды. Для записи решения волнового уравнения (1) подобно решению для
диэлектрика введем вспомогательные параметры согласно соотношениям:
- омической проводимостью
среды. Для записи решения волнового уравнения (1) подобно решению для
диэлектрика введем вспомогательные параметры согласно соотношениям:
где
![]()
где
![]() и
и
![]() - вещественные
величины,
- вещественные
величины, ![]() -
комплексный показатель преломления среды. Тогда решение уравнения Гельмгольца
(1) в проводящей среде запишем в виде:
-
комплексный показатель преломления среды. Тогда решение уравнения Гельмгольца
(1) в проводящей среде запишем в виде:
где ![]() - волна напряженности
электрического поля, распространяющаяся вдоль оси х, с начальной
амплитудой
- волна напряженности
электрического поля, распространяющаяся вдоль оси х, с начальной
амплитудой ![]() .
.
Согласно
соотношению (6) интенсивность электромагнитной волны ![]() ослабляется
в е раз на расстоянии
ослабляется
в е раз на расстоянии ![]() ,
называемом толщиной скин-слоя.
,
называемом толщиной скин-слоя.
Подставляя
соотношение (2) для комплексной проводимости в выражение (3) для ![]() и полагая
и полагая
![]() , получим:
, получим:
Из
соотношения (7) следует, что при увеличении концентрации свободных носителей
заряда вещественная часть ![]() уменьшается и
при
уменьшается и
при ![]() 1021 м-3
обращается в нуль, если положить
1021 м-3
обращается в нуль, если положить ![]() 10l2 c-1,
10l2 c-1, ![]() . При этих условиях
. При этих условиях
![]() ;
следовательно,
;
следовательно, ![]() .
Приближенно на основании формул (5) можно считать, что :
.
Приближенно на основании формул (5) можно считать, что :
Соотношение (6) и (8) определяют волну в однородной проводящей среде. Для рассмотрения прохождения волны через плоскослоистую среду требуется определение амплитуд проходящих и отраженных волн по формулам Френеля и учет интерференции отраженных волн с падающей. В работе [3] методом ориентированных графов получено достаточно громоздкое выражение для коэффициента прозрачности трехслойного экрана при нормальном падении изучения его на поверхность. Применим это решение к трехслойной структуре: 1- слой воздуха, 2 – область пространственного заряда (ОПЗ) на поверхности защитного покрытия, 3 – слой покрытия с объемными параметрами.
Толщина
слоя ОПЗ составляет величину порядка дебаевской длины экранирования ![]() и, как показывают
оценки,
и, как показывают
оценки,![]() при
частоте
при
частоте ![]() 1 ГГц.
В этом частном случае выражение для коэффициента прозрачности электромагнитного
излучения имеет вид:
1 ГГц.
В этом частном случае выражение для коэффициента прозрачности электромагнитного
излучения имеет вид:
Положив
для оценки
![]() =1;
=1; ![]() =3;
=3; ![]() = 30 (Ом-м)-1;
= 30 (Ом-м)-1;![]() =1,4*10-4 м,
в соответствии с формулой (9) получим, что коэффициент отражения
=1,4*10-4 м,
в соответствии с формулой (9) получим, что коэффициент отражения
![]() . Из полученных
данных следует, что даже очень тонкий слой ОПЗ, толщиной менее половины толщины
скин-слоя имеет весьма низкий коэффициент прозрачности.
. Из полученных
данных следует, что даже очень тонкий слой ОПЗ, толщиной менее половины толщины
скин-слоя имеет весьма низкий коэффициент прозрачности.
Литература
1. Грудинская Г.П. Распространение радиоволн. - М.:Высшая школа,1975.280 с.
2. Борн М., Вольф Э. Основы оптики. - М.: Наука, 1970. 850 с.
3. Семенов М. Техническая электродинамика. - М.: Связь,1973. 480 с.
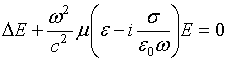 , (1)
, (1)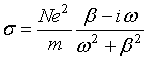
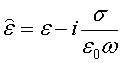
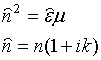 ,
(4)
,
(4)