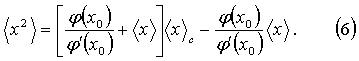|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 6, 2006 |
|
О статистической погрешности измерения среднего
квадрата
случайной функции
Е.С. Саркисян
Институт радиотехники и электроникик РАН
Получена 11 декабря 2006 г.
Вычислена дисперсия оценки среднего квадрата случайной функции (сигнала) при использовании двух методов измерения: “прямого” и с применением генератора случайных импульсов, управляемого исследуемым сигналом. Показано преимущество второго на примере конкретного вероятностного распределения значений исследуемой функции. Затронут вопрос реализации требуемых управляемых генераторов на основе полупроводниковых приборов с лавинным пробоем р-п перехода.
При экспериментальном исследовании систем, описываемых аппаратом случайных функций (процессов) наиболее часто представляет интерес измерение моментов низших порядков. Важна, в частности, энергетическая характеристика – средний квадрат процесса.
В нижеследующем рассматривается измерение среднего квадрата стационарного случайного процесса, например, напряжения на выходе некоторого электронного блока, т.е. второго момента одномерного распределения вероятностей мгновенных значений процесса [1] и производится сравнение статистической точности для двух способов измерения.
Будет предполагаться выполненным условие эргодичности, позволяющее получать этот параметр, например, усреднением во времени квадрата некоторой реализации x(t) случайного процесса [2].
В ряде измерений рассматриваемого типа целесообразно оперировать набором значений xi выбранной реализации , отсчитанных в достаточно далеко отстоящие друг от друга моменты времени ti (i=1,2….N), являющиеся в общем случае случайными, так что обеспечивается независимость отсчетов. В качестве ti могут выступать, например, моменты появления импульсов на выходе некоторого автономного генератора случайных сигналов.
В [3] содержится способ измерения моментов вероятностного распределения, в соответствии с которым подлежащие обработке отсчеты xi рассматриваемой реализации процесса производятся в моменты времени, вероятностным образом зависящие от поведения x(t). Для реализации способа достаточно иметь генератор импульсов, управляемый исследуемый процессом и вырабатывающий в малом временном интервале (t, t+∆t) импульс с вероятностью пропорциональной ∆t
где коэффициент пропорциональности- строго монотонная функция мгновенного значения процесса, характеризующая генератор импульсов. Выполнение (1) означает, что при x(t)= const на выходе генератора имеется пуассоновский поток импульсов с интенсивностью равной j(x). (Подобная ситуация имеет место на выходе фотоэлектронных умножителей при неизменном освещении).
Измерение второго момента áx2ñ (угловые скобки означают усреднение по множеству) случайной функции удобно производить при использовании генератора с функцией j(x) прямо пропорциональной x.
Пусть некоторым образом обеспечен отсчет любого количества значений xс выбранной реализации в моменты появления импульсов этого генератора. В этом случае вероятностное распределение множества отсчетов xс, которое могло быть произведено за бесконечное время, имело бы плотность распределения вероятностей (ПРВ)
где p(x) – одномерная ПРВ значений процесса, со средним
Ввиду независимости отсчетов в данном случае можно также утверждать, что сечение процесса, проведенное, например, через моменты появления i-го (для каждой из идентично обрабатываемых реализаций процесса) импульса генератора, определяет случайную величину с ПРВ pc(x). Соответственно, N отсчитанных значений xci могут рассматриваться и как выборки из множества значений случайной величины, определенной указанным образом.
Оценку áx2ñcоц среднего квадрата, т.е. значение, приписываемое ему после измерений xci, можно записать в виде
где
где xi есть отсчет функции x(t) в момент ti , заданный автономным генератором импульсов. Для простоты общее число отсчетов в каждом из двух наборов их взято одинаковым, а для индекса при t в двух разных наборах времен использована одна и та же буква.
"Прямая" оценка величины áx2ñ имеет вид
с дисперсией
Дисперсию оценки той же величины, измеряемой с вовлечением отсчетов xci, несложно записать в случае допустимости пренебрежения флуктуациями áxñоц, т.е. при
:
Учет разброса áxñоц при независимых, например, сделанных на разных временных интервалах áxсñоц и áxñоц , следующий
Вклад второго слагаемого практически пренебрежим во многих случаях. Выражая величины в (4) через параметры исходного распределения p(x), и выпуская второе слагаемое, имеем
В формулах (3) и (5) в отличие от (2) нет четвертого момента случайной функции. Поэтому результат вычисления по (3) или (5) может оказаться меньше, чем число, вычисленное по (2).
Если при "прямом" измерении (оценке) вместо предполагавшейся однополярной оперировать центрированной случайной величиной
при предварительно измеренном áxñ
(ср.[4] ), формула (2) перепишется в виде
что улучшает ситуацию, но выражение опять содержит четвертый момент. Вычисление дисперсии по формуле (5) и формулам (2) и (2’) дает, например, в случае исходной экспоненциальной ПРВ значений процесса отношение дисперсий 6/20 и 6/8 соответственно.
Вычисление D[áxcñоцáxñоц ] в случае xci и xi, отсчитанных на одном и том же временном интервале, представляется затруднительным. Здесь оправдано, и экспериментальное исследование погрешностей, даваемых упомянутыми выше способами. Принципиально несложный расчет предельной дисперсии в допущении полностью коррелированных перемножаемых оценок, т.е., при равенстве соответствующих нормированных случайных величин связан с громоздкими преобразованиями и , по-видимому, не адекватен практической ситуации.
Реализация генератора, управляемого выборочной функцией исследуемого процесса, допускает разнообразие подходов. В одном из ранних устройств подобного типа [5] используются электрические шумы тиратрона. Вполне приемлем фотоэлектронный умножитель, управляемый интенсивностью падающего на фотокатод излучения; он обеспечивает j(x) ~ x в широком диапазоне интенсивностей. Перспективным представляется использование для генерации требуемых импульсов процесса лавинного пробоя (ЛП) p-n перехода полупроводниковых приборов. Экспоненциальное распределение временных интервалов (на определенном отрезке значений) между импульсами лавинного тока [6] свидетельствует о наличии пуассоновского потока импульсов. Некоторые возникающие при этом особенности состоят в следующем. Для начальной области напряжений пробоя перехода характерным для вырабатываемых на нагрузке полупроводника импульсов [3] является, в общем случае, нелинейная зависимость приращения x к напряжению начала пробоя и интенсивности потока регистрируемых импульсов. При этом протяженность интервала напряжений, на котором с достаточной точностью j(x) ~ x, может оказаться порядка помех или неизбежных пульсаций питающего напряжения. В такой ситуации возможно использование некоторого участка исходной характеристики, описываемого
с отличной от нуля интенсивностью потока импульсов в его начале и исследуемым сигналом x(t), наложенным на напряжение x0 начала этого участка. Тогда для среднего квадрата процесса можно получить
Из (6) видно, что по-прежнему выражение для
не будет содержать
, а также, что желательны меньшие отношения
. Отметим, что в случае заметных флуктуаций
при определенных обстоятельствах целесообразно учитывать, что средняя интенсивность потока импульсов при измерении
есть
, что может быть измерено независимо.
При использовании ЛП светодиодов [3] в управляемом генераторе расширяются возможности формирования характеристик j(x) за счет генерации светом зарядов, инициирующих лавину в p-n переходе [6].
Автор выражает признательность заведующим лабораторий проф. В.Г. Шаврову и проф. В.В. Григорьянцу за содействие в выполнении данной работы.
СПИСОК ЛИТЕРАТУРЫ
1. С.М. Рытов, Введение в статистическую радиофизику, ч.1, М. 1976., С.106-108;
2. Дж. Бендат, А. Пирсол, Измерение и анализ случайных процессов, М., Мир, 1974, С.203;
3. Описание заявки ИРЭ РАН №20005125450/22 на выдачу патента РФ на ПМ “Преобразователь вероятностных характеристик сигнала” (патент № 51448);
4. Г.Я. Мирский, Характеристики стохастической взаимосвязи и их измерения, М., Энергоиздат, 1982, С.256;
5. Л.В.Сытенко, Управляемые генераторы случайной последовательности импульсов, Сб. "Автоматика и вычислительная техника", Зинантне, Рига, 1965, Т.10, С.189-209.
6. И.В.Грехов, Ю.Н. Сережкин, Лавинный пробой p-n перехода в полупроводниках, Ленинград, Энергия, 1980.
Автор: Евгений Санатрукович
Саркисян, sarkis@cplire.ru,
ИРЭ РАН
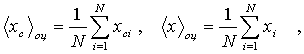
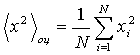
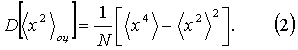
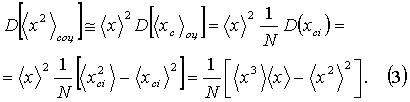
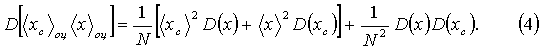
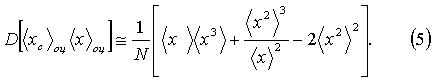
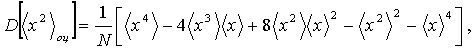 (2’)
(2’)