УДК 621.396.96

ВОЗМОЖНОСТЬ  ВЫДЕЛЕНИЯ  ИНФОРМАЦИИ  ОБ  УГЛОВОЙ СКОРОСТИ  ПОВОРОТА  ВОЗДУШНОГО  ОБЪЕКТА

ПО  ПОСЛЕДОВАТЕЛЬНОСТИ  ОТРАЖЕННЫХ  СИГНАЛОВ

 

А. Г. Прохоркин, Д. Г. Митрофанов, В. В. Бортовик, Д. А. Майоров, В. А. Перехожев

 Военная академия войсковой противовоздушной обороны Вооруженных Сил  Российской Федерации имени Маршала Советского Союза А. М. Василевского

 

Получена 14 декабря 2011 г.

 

Аннотация.  Описывается методика и результаты натурного эксперимента, подтверждающего возможность достоверного измерения угловых скоростей поворота летательного аппарата при траекторных нестабильностях полета на основе корреляционной характеристики или характеристики изрезанности, сущность формирования которой поясняется. Указанные характеристики сформированы цифровым способом по радиолокационным отражениям от реального летательного аппарата.  Количественно оценена мера сходства формируемых характеристик с истинным законом изменения скорости поворота объекта. Показано влияние различных факторов на информативность оценочных характеристик.

Ключевые слова: траекторные нестабильности полета, корреляционная характеристика, характеристика изрезанности, натурный эксперимент.

Abstract. The method and results of full-scale experiment, confirming the possibility of angular velocity meaningful measurement of an airborne by trajectory flight instabilities on base of correlation characteristics or angularity characteristics are described, the essence  of which is explained. The mentioned characteristics are formed by a digital method on radar images from the real airborne. The similarity measure of forming characteristics with true objects rotating law of variation is computed. The influence of different factors on self descriptiveness estimate characteristics is shown.

Keywords: trajectory flight instabilities, correlation characteristic, angularity characteristic, full-scale experiment.

 

Введение

Нынешний этап развития радиолокации отличается переходом от грубого определения координат и отражающей способности объектов к извлечению информации об их геометрических особенностях, размерах, поведении в полете. Сегодня прогрессивными и перспективными считаются методы радиовидения, инверсного радиолокационного синтезирования апертуры (ИРСА), сверхразрешения и т. п. Эти подходы обеспечивают формирование радиолокационных изображений (РЛИ) воздушных объектов (ВО), используемых в системах контроля и идентификации.

При этом известные методы формирования двумерных РЛИ [1] всегда используют в качестве физической основы повышения поперечной разрешающей способности изменение ракурса ВО. Причем скорость и направление углового перемещения ВО предполагаются неизменными, что в условиях турбулентности не соответствует действительности. А алгоритмы адаптации РЛИ к изменению величины угловой скорости поворота летательного аппарата (ЛА) не могут быть использованы при отсутствии достоверной информации о характере происходящих изменений. Отсутствие нужды в измерении угловой скорости поворота ВО до появления методов радиовидения явилось причиной того, что соответствующие алгоритмы и подходы научными школами не прорабатывались и не развивались. В то же время истинное значение угловой скорости поворота ЛА при ИРСА определяет важнейший результат метода – величину элемента поперечного разрешения отражателей на поверхности ВО.

Поиск радиолокационных способов измерения поперечных размеров ВО по протяженности доплеровских портретов [2] привел к выводу о том,  что ширина портрета должна измеряться не на произвольном, а на специально выбранном интервале ИРСА, где угловая скорость рысканий планера ЛА минимальна по абсолютной величине. Для выбора такого интервала анализа необходимо накапливать избыточное число отражений и проводить с массивом этих отражений детальный и тонкий корреляционный анализ. Вскрытая закономерность изменения ширины доплеровского портрета в соответствии с изменением коэффициента автокорреляции на участке отражательной характеристики (ОХ) ВО вызвала появление гипотезы о возможности оценки угловой скорости поворота ВО по поведению корреляционной характеристики (КХ) или характеристики изрезанности (ХИ).

Для нахождения информативных интервалов ИРСА в работах [2-4] были предложены способы косвенной оценки угловой скорости рысканий сопровождаемого ЛА. Однако работоспособность этих способов проверялась лишь с помощью математического моделирования и по статистическим результатам исследования структуры получаемых доплеровских портретов. Истинные причины получения эффективных оценок поперечных размеров ВО доказаны не были, так как при обработке экспериментальных данных отсутствовала возможность сопоставления и сравнения параметров выявленных внешним способом траекторных нестабильностей (ТН) с реальным поведением ЛА в полете.

Целью данной статьи является экспериментальное подтверждение возможности адекватной оценки угловой скорости поворота ВО, т. е. выявления закона изменения угловой скорости на основе корреляционного анализа фракций отраженных сигналов.

 

Методика эксперимента.

Для подтверждения выдвинутой гипотезы о возможности адекватной оценки параметров ТН (угловых скоростей поворота) ЛА с помощью корреляционной характеристики и ХИ в октябре 2011 г. была проведена серия натурных экспериментов в рамках гранта РФФИ № 11-07-97517. Главной особенностью проводимых экспериментов являлась синхронная регистрация углового положения (изменения углового положения) планера ЛА и комплексных амплитуд сигналов, отраженных самолетом в сантиметровом диапазоне волн в режиме автоматического сопровождения. Для проведения натурных экспериментов была разработана оригинальная методика синхронной регистрации данных и соответствующее программное обеспечение, позволяющее изучать и обрабатывать цифровую информацию после завершения радиолокационного и полетного экспериментов.

Методика проведения натурного эксперимента синхронной регистрации данных включала в себя следующие основные элементы:

1. Разработка полетного задания привлекаемому ЛА для обеспечения эксперимента. Полетное задание предусматривало осуществление записей отраженных от ВО сигналов на встречных, догонных и боковых ракурсах наблюдения. При этом в интересах наиболее достоверной оценки степени влияния ТН пилотам самолета на контролируемых участках маршрута было предписано выдерживать прямолинейную траекторию без изменения скорости и высоты. Схема полетного задания приведена на рис. 1.

 

 

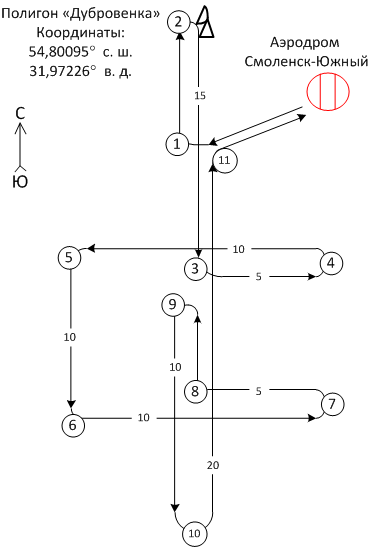
Рис. 1.  Схема полетного задания.

 

2. Оборудование ЛА устройством контроля и регистрации его положения в пространстве, а РЛС – устройством регистрации квадратурных составляющих отраженных от ВО радиолокационных сигналов.

3. Синхронизация устройств регистрации, находящихся в аппаратном отсеке РЛС и на борту ЛА. Непосредственно перед началом проведения натурных экспериментов персональные компьютеры связывались в сеть и синхронизировались по сетевому серверу времени.   

4. Непосредственное проведение синхронных записей данных на борту ЛА и в контрольной точке приемной системы РЛС. Запись информации о положении ЛА в пространстве с помощью навигационной аппаратуры осуществлялась непрерывно. Регистрация радиолокационных сигнатур в РЛС производилась по команде руководителя эксперимента после взятия ЛА на автоматическое сопровождение.

5. Предварительная обработка данных эксперимента. Сущность предварительной обработки заключалась в сравнении координат контрольных точек траектории полета сопровождаемого воздушного объекта, измеренных РЛС, с зарегистрированными   данными    аппаратуры   спутниковой   навигации   ГЛОНАСС/GPS, установленной на борту самолета.

6.  Обработка зафиксированных экспериментальных данных. При этом из генеральной совокупности экспериментальных записей выделяются частные выборки, синхронно зарегистрированные в РЛС и на борту самолета. Из массивов квадратурных составляющих отраженных сигналов формируются косвенные оценки угловой скорости изменения ракурса ВО. Проводится расчет модульного значения истинной угловой скорости изменения курса ЛА по данным навигационной системы. Проверяется соответствие реальной угловой скорости изменения ракурса ЛА ее оценкам, сформированным с помощью КХ и ХИ.

Для контроля реального положения в пространстве летательного аппарата в ходе проведения экспериментов использовался комплекс спутниковой навигации ГЛОНАСС/GPS стандартной точности и инерциальной навигации, модель КСН-Н (разработка НИИ СТТ г. Смоленск). Структурная схема блока представлена на рис. 2.

Процессор обеспечивал преобразование данных, поступающих с трехстепенных датчиков акселерометров и гироскопов в значения текущих углов крена, тангажа и курса положения планера ЛА в пространстве.

 

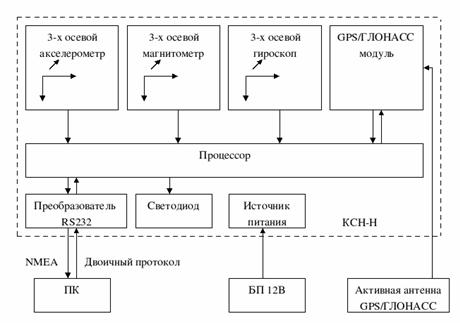
Рис. 2. Структурная схема КСН-Н.

 

Текущие значения углов, а также координат положения ЛА по данным спутниковой навигации ГЛОНАСС/GPS через порт данных RS232 регистрировались персональным компьютером. Питание аппаратуры осуществлялось от автономного источника напряжением 12 В. Размещение навигационной аппаратуры осуществлялось в транспортном отсеке самолета Ан-2. Внешний вид аппаратуры навигации представлен на рис. 3.

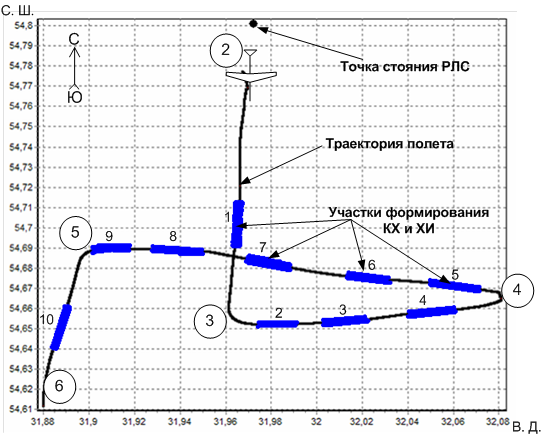
Участок реальной траектории полета самолета Ан-2, находящийся между второй и шестой контрольными точками полетного задания, представлен на рис. 4. Для формирования данной траектории использовались координаты, зарегистрированные в ходе экспериментов с помощью навигационной аппаратуры  по данным спутниковой системы ГЛОНАСС/GPS.

 

 

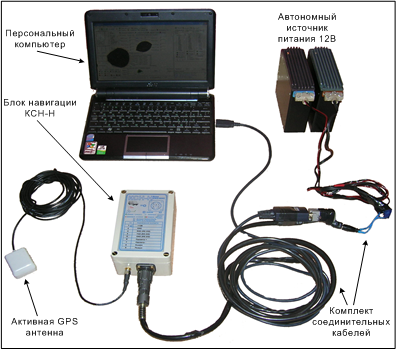
Рис. 3. Внешний вид устройства регистрации положения ЛА в пространстве.

 

 

 

Рис. 4.  Реальная траектория полета самолета Ан-2.

Утолщенные линии на траектории полета самолета указывают участки, для которых по отраженным сигналам производилось формирование КХ и  ХИ с последующим их сравнением с реальными угловыми перемещениями ЛА в пространстве.

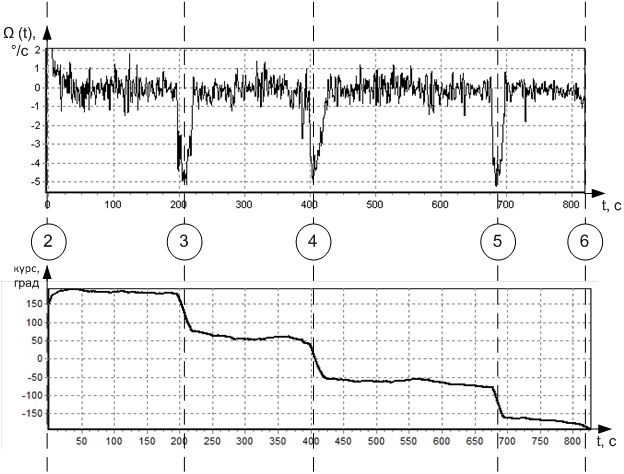
На рис. 5 показаны зависимости курса g самолета и угловой скорости его поворота W (^о/с), на временном интервале, соответствующем участку траектории экспериментального полета, представленному на рис. 4.

 

 

Рис. 5. Угловая скорость поворота и курс и самолета Ан-2.

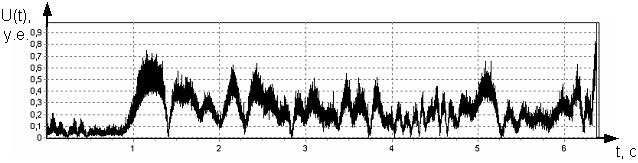
Регистрация квадратурных составляющих отраженных сигналов в радиолокационной станции сантиметрового диапазона осуществлялась на выходе предварительного усилителя промежуточной частоты. Согласно ранее разработанным и примененным методикам [5] регистрирующая аппаратура осуществляла непрерывное преобразование сигнала в цифровой код. С помощью цифрового фазового детектора осуществлялось детектирование и разложение отсчетов отраженного сигнала на квадратурные составляющие, запоминаемые в памяти компьютера. Вариант модуля комплексной огибающей сжатых в процессе согласованной обработки отраженных сигналов представлен на рис. 6. По оси абсцисс отложены временные отсчеты, соответствующие одному из периодов зондирования пространства.

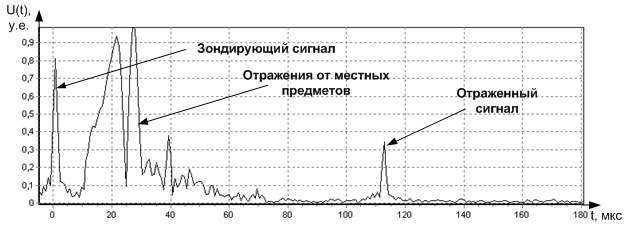
Рис. 6. Огибающая отраженного сигнала в на промежуточной частоте после цифрового фильтра для самолета Ан-2 на дальности D=16 км.

 

Для формирования ОХ в каждом периоде повторения после процедуры сжатия цифровым фильтром определялось положение максимума отклика фильтра на отраженный от ВО сигнал. В этой точке определялись значения амплитуды и фазы сжатого сигнала, которые записывались в массив. Сформированный таким образом массив представлял комплексную ОХ ВО. При графическом представлении ОХ использовались модульные значения u(t_i) комплексных отсчетов массива отраженных сигналов u_Re(t_i) и u_Im(t_i) на имеющемся временном интервале сопровождения:

; ,                   (1)

где К – количество сигналов, используемых для построения ОХ.

Пример ОХ, представленный массивом последовательности отраженных самолетом Ан-2 сигналов, приведен на рис. 7. Указанная ОХ соответствует участку № 7 траектории полета Ан-2, представленной на рис. 4.

 

Экспериментальные результаты и их обсуждение.

Формирование ХИ в интересах оценки участков отраженных сигналов, соответствующих различным угловым скоростям поворота цели, производилось следующим образом. Из последовательности значений u(t_i) в отдельный массив записывались частные выборки (ЧВ) длительностью Т_чв, смещенные друг относительно друга на Т_см. Между одноименными элементами массивов ЧВ производился расчет приращений амплитуды.

 

 Рис. 7. Участок экспериментальной ОХ самолета Ан-2 на ракурсе 180^о и дальности 15,2 км.

 

Рассчитанные приращения амплитуд усреднялись и запоминались в качестве одного отсчета ХИ. Положение рассчитанного отсчета ХИ соответствует середине интервала записи ЧВ в пределах генеральной последовательности зафиксированных данных. Для расчета следующего отсчета ХИ из генеральной последовательности данных извлекалась очередная частная ЧВ путем смещения относительно предыдущей на один отсчет в пределах генеральной совокупности. Вся ХИ формировалась путем последовательного смещения ЧВ в пределах фракции отраженных от ВО сигналов.

Поскольку при формировании ХИ производился расчет приращений между амплитудами отраженных сигналов, то проявление турбовинтового эффекта (ТВЭ) в виде высокочастотной модуляции отраженных сигналов оказывало негативное влияние на результаты расчета и построения ХИ. Изрезанность ОХ за счет ТВЭ не зависит от угловой скорости поворота ЛА. Поэтому при построении ХИ модуляция, обусловленная проявлением ТВЭ, подлежала компенсации.

Частота турбовинтовых гармоник на несколько порядков превышает частоту флюктуаций сигнала, отраженного планером ВО. Следовательно, период турбовинтовых флюктуаций на несколько порядков меньше, чем период амплитудных флюктуаций, выраженных во временной протяженности лепестков ОХ. Ширина лепестка ОХ  Dq определяется поперечными размерами ЛА L_^ и длиной волны l (). Время формирования лепестка ОХ Т_л зависит от угловой скорости поворота ЛА  (). Период появления всплесков амплитуды за счет влияния ТВЭ определяется частотой вращения лопастей и их количеством. Выражение для расчета периода появления всплесков имеет вид . Если для устранения влияния ТВЭ использовать сглаживание, то длина усредняющей выборки принимается равной половине интервала формирования наиболее узкого лепестка ОХ. Это обеспечивает наилучшее подавление турбовинтовых амплитудных флюктуаций отражений при сохранении формы низкочастотной огибающей. Формирование сглаженной амплитудной огибающей ОХ описывается выражением

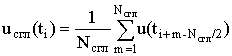;                                    (2)

,                                                

где  N_сгл – количество сигналов, используемых для сглаживания.

В результате сглаживания реальной ОХ (см. рис. 7) формируется так называемая планерная низкочастотная ОХ ВО, показанная на рис. 8. Необходимое для сглаживания число сигналов N_сгл в частной выборке определяется условием

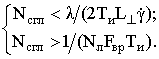                                               (3)

 

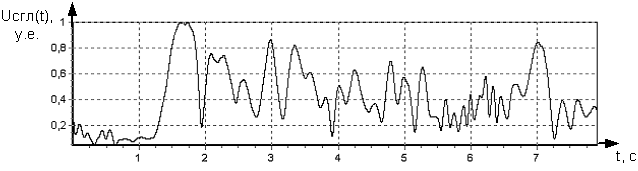
Рис. 8. Сглаженная ОХ летательного аппарата типа Ан-2.

 

 

Формирование ХИ осуществлялось по отсчетам сглаженной ОХ  u_сгл(t_i)  и описывалось выражением

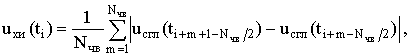                   (4)

где    ; N_чв – число отсчетов сигнала в ЧВ.

Результат формирования ХИ с использованием выражения (4) в графическом виде представлен на рис. 9.

 

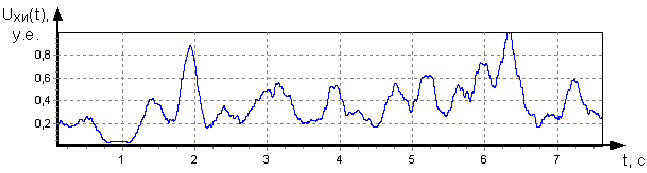
Рис. 9.  Характеристика изрезанности отражений от Ан-2.

 

Для удобства поиска в полученной ХИ локальных максимумов и минимумов также производили ее сглаживание, в итоге которого несущественные локальные экстремумы пропадали.

В интересах исключения потери полезной информации о положении интервалов отражений, соответствующих различной угловой скорости поворота ЛА, длительность ЧВ для сглаживания ХИ не должна превышать минимального полупериода ТН. Значит, выражение для расчета значений сглаженной ХИ должно иметь вид

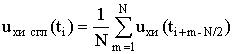                                      (5)

с учетом

  ,                                       (6)

 

где Т_тн – минимальный полупериод рысканий ВО при ТН полета; Т_и – период повторения импульсов РЛС; N – число отсчетов выборки сглаживания.

В связи с тем, что увеличение длительности ЧВ приводит к более гладкой форме ХИ, выбирают, как правило, наибольшую из возможных по длительности ЧВ, определяемую минимальным полупериодом рысканий планера. Опираясь на экспериментальные данные для оценки угловых скоростей поворота ЛА, совершающего полет в неспокойной атмосфере, целесообразно рекомендовать использование частных выборок сглаживания длительностью от 0,1 до 0,5 с.

Однако длительность ЧВ сглаживания не может быть признана единственным параметром, влияющим на достоверность (качество) информации о поведении ЛА в полете. В процессе изучения способов адаптации алгоритмов формирования РЛИ к поведению ВО, движущегося с ТН, было установлено, что информативность КХ или ХИ, т. е. яркая выраженность их экстремумов, в определенной мере зависит от целой совокупности параметров их формирования. Использование экспериментальных данных о реальной угловой скорости вращения сопровождаемого ВО предоставляет возможность реально оценить степень влияния параметров формирования КХ и ХИ на их информативность. Это обеспечивает возможность подбора оптимальных параметров формирования информационных характеристик (КХ, ХИ).

В качестве критерия соответствия реальной угловой скорости поворота ЛА и оценок, формируемых на основе КХ и ХИ, предложено использовать правило (метод) наименьших квадратов [6], предполагающее вычисление показателя вида

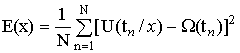,                             (7)

где x – варьируемый параметр (например, в качестве x может использоваться относительный временной сдвиг Dt между синхронно зафиксированными отсчетами оценочной характеристики (КХ, ХИ) и истинного закона изменения углового положения ЛА); U(t_n/x) – значение оценочной характеристики (КХ, ХИ) в момент времени t_n при определенной величине параметра х; Ω(t_n) – величина истинной угловой скорости вращения ЛА в момент времени t_n.

К сожалению, КХ и ХИ предоставляют только относительные сведения о значениях угловой скорости поворота ВО. В связи с этим на исследуемом интервале времени наблюдения целесообразно проводить нормировку значений ХИ U_хи(t), КХ U_кх(t) и угловой скорости ВО Ω(t) в диапазоне от 0 до 1. Поскольку согласно методике эксперимента записи проводились синхронно, то глобальные экстремумы функций должны наилучшим образом соответствовать друг другу при Dt=0. Правильная реакция параметра E(x) на временное смещение оценок относительно истинных значений подтверждает его пригодность для проведения исследований. На рис. 10 приведена характеристика сходимости истинных значений и оценок угловых скоростей для вариантов использования КХ и ХИ (участок № 8 рис. 4). В качестве параметра х использовался сдвиг по времени Dt  между начальными (контрольными) точками оценочных характеристик и соответствующими точками реального закона изменения угловой скорости вращения ЛА. Зависимость параметра сходимости U_сх(x)=E(Dt) от величины Dt сформирована для диапазона временных сдвигов от –2 до +2 с.

 

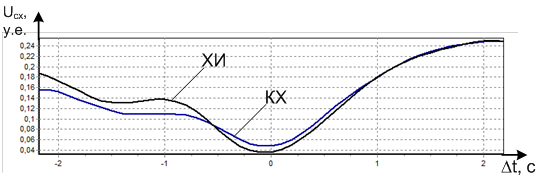
Рис. 10.  Характеристики сходимости КХ и ХИ с истинным законом изменения Ω(t) при их смещении по времени.

 

Заметно, что увеличение смещения Dt между сформированными КХ (ХИ) и истинным законом изменения угловой скорости ЛА W(t) приводит к возрастанию степени их несовпадения. Иначе говоря, увеличение значений параметра сходимости U_сх(Dt) закономерно отображает относительную величину расхождения нормированных КХ (ХИ) с истинным законом Ω(t). Это подтверждает применимость параметра E(x)=U_сх(x) для исследования степени влияния частных параметров формирования КХ и ХИ на их информативность.

Оценивать информативность КХ и ХИ предложено путем исследования величины U_сх(х) при временном сдвиге Dt=0 и вариациях параметров формирования оценочных характеристик. Величина параметра x, при которой значения оценки U_сх(х) являются минимальными, признавалось оптимальным в рассматриваемых условиях локации ВО.

Как показало моделирование и обработка данных эксперимента [7], при формировании ХИ основными варьируемыми параметрами являются длительность (длина) частных выборок Т_чв и временной разнос между ними DТ_чв, т.е. между смежными ЧВ. На рис. 11 приведены результаты расчетов параметра сходимости U_сх(DT_чв) при изменении DТ_чв от 2 до 100 мс и трех фиксированных значениях длительности ЧВ, а именно 205, 478 и 684 мс.

 

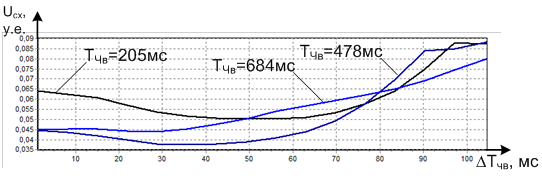
Рис. 11.  Характеристики сходимости ХИ с истинным законом Ω(t) при изменении временного разноса между смежными ЧВ.

 

Как следует из рис. 11, различным длительностям частных выборок T_чв соответствуют разные значения интервала смещения DT_чв, обеспечивающие минимизацию оценки сходимости. Например, наилучшая сходимость при длительности ЧВ Т_чв=478 мс обеспечивается смещением DT_чв=41 мс. При использовании Т_чв=684 мс для получения наилучшей сходимости необходимо уменьшать величину смещения ЧВ до 28 мс, а при Т_чв=205 мс – наоборот увеличивать DT_чв  до  52 мс.

Для поиска оптимального значения длительности Т_чв в диапазоне от 300 до 700 мс были получены характеристики сходимости при фиксированных смещениях DT_чв, равных 27, 36 и 44 мс. Они показаны на рис. 12.

 

Рис. 12.  Характеристики сходимости  ХИ с истинным законом изменения  угловой скорости поворота ЛА Ω(t) при изменении Т_чв.

 

Можно заметить, что при увеличении длительности ЧВ для получения наилучшего совпадения ХИ с Ω(t) необходимо уменьшать временной сдвиг DТ_чв, и наоборот. Наилучшая сходимость наблюдается при смещении ЧВ на DT_чв=36 мс и длительности Т_чв=507 мс. Такие параметры приводят к минимизации параметра сходимости в точке глобального минимума до величины U_сх(Т_чв)=0,037.

         При формировании КХ к основным влиятельным параметрам относятся длительность ЧВ Т_чв и номер информативного отсчета N_АКФ в автокорреляционной функции (АКФ), соответствующего оценочному времени корреляции t_оц [3,4] в пределах главного лепестка АКФ. Зависимость параметра сходимости от величины Т_чв для различных фиксированных значений  N_АКФ  представлена на рис. 13.

 

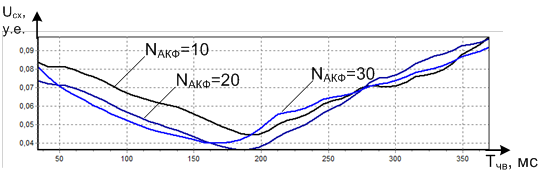
Рис. 13. ­ Характеристики сходимости ХИ с истинным законом Ω(t) при изменении длительности Т_чв, используемой для построения КХ.

 

Анализ иллюстрируемых рис. 13 характеристик сходимости показывает, что наименьшего значения параметр сходимости U_сх(Т_чв) достигает при применении ЧВ с длительностями от 160 до 200 мс.

Для исследования информативности номеров отсчетов, используемых для определения коэффициентов корреляции в пределах главного лепестка АКФ, формировали множество КХ по коэффициентам, соответствующим анализируемым отсчетам, и вычисляли результирующую меру сходимости U_сх(N_АКФ). Расчет сходимости оценок проводили при изменениях N_АКФ в диапазоне от 2 до 50 при фиксированных значениях Т_чв. Результаты исследования в графическом виде демонстрируются рис. 14.

 

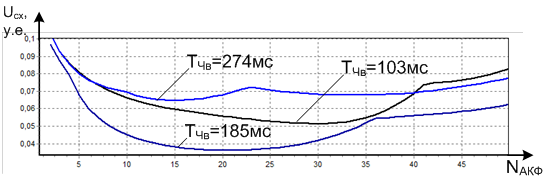
Рис. 14. ­ Характеристики сходимости КХ с истинным законом Ω(t) в зависимости от номера отсчета в главном лепестке АКФ, используемого для определения коэффициента автокорреляции.

 

Наименьшее значение (0,036) параметр сходимости принимает при N_АКФ=20. Изменение N_АКФ в диапазоне от 15 до 25 и фиксированном Т_чв=185 мс не ведет к ухудшению сходимости. Величина U_сх(N_АКФ) на этом интервале при Т_чв=185 мс изменяется незначительно, что свидетельствует о слабом влиянии данного параметра на результат формирования КХ. Расширение диапазона изменения N_АКФ либо изменение длительности ЧВ приводит к существенному увеличению расхождения КХ с реальным законом изменения угловой скорости поворота ВО.

Таким образом, проведенные исследования позволили рекомендовать для формирования ХИ частные выборки отражений длительностью от 400 до 600 мс, смещая их друг относительно друга на 25–50 мс. Для построения информативной КХ целесообразно использовать ЧВ длительностью от 160 до 210 мс и применять для определения коэффициента автокорреляции отсчеты главного лепестка АКФ с 14 по 27. Применение указанных параметров позволяет формировать оценочные характеристики, степень расхождения которых с реальным законом изменения Ω(t) в районах глобальных экстремумов по предложенному критерию не превышает 0,04.

На рис. 15 (а) и 15 (б) представлены КХ и ХИ, сформированные для участка № 7 траектории полета Ан-2, выделенного утолщенной линией на рис. 4. Для этого же участка траектории на рис. 5 (в) приведена зависимость угловой скорости изменения ракурса локации ВО, сформированная с помощью навигационной аппаратуры. При формировании КХ и ХИ были учтены рекомендации, сделанные в отношении основных параметров, влияющих на их информативность. 

 

 

Рис. 15. Оценка параметров ТН: а) корреляционная характеристика;

 б) характеристика изрезанности;  в) угловая скорость поворота Ан-2.

 

Наилучшее совпадение оценок КХ и ХИ с реальными значениями W(t) ЛА наблюдалось при большой угловой скорости вращения ВО (участок e). При более низких значениях W (интервалы а-d) могут наблюдаться небольшие расхождения в оценках. Например, на участках а и b  ХИ с высокой достоверностью отражает реальную угловую скорость поворота ЛА, в то время как КХ дает неверную информацию. Между участками c и d  КХ и ХИ дают инвертированные оценки. Ошибки объясняются влиянием множества внешних факторов различной природы. Такими факторами могут быть проявление ТВЭ, различного рода шумы и помехи, появление в поле зрения РЛС дополнительных рассеивающих центров на планере ЛА, приводящее к резкому изменения амплитудно-фазовых характеристик и т. д. Однако в целом КХ и ХИ достаточно достоверно отражают участки, где угловая скорость изменения ракурса локации (поворота планера) ЛА имеет максимальные значения.

Таким образом, результаты обработки данных, полученных в ходе натурных экспериментов, показывают, что по расположению глобальных экстремумов КХ и ХИ путем анализа всегда можно определить положение интервалов, на которых угловая скорость поворота имеет максимальные значения. Следовательно, рассмотренные алгоритмы формирования оценок параметров ТН полета ВО могут быть рекомендованы к использованию в системах радиовидения,  классификации, идентификации, а также в аэродромных системах контроля безопасности воздушного движения при дистанционной оценке параметров полета воздушных судов и  т. д.

 

Исследования выполнены при финансовой поддержке администрации Смоленской области и Российского фонда фундаментальных исследований.

 

Литература

 

1.      Shirman Y. D. Computer simulation of aerial target radar scattering recognition, detection, and tracking. Norwood. Boston-London. Artech House, 2002.  296 p.

2.      Митрофанов Д. Г., Прохоркин А. Г., Нефедов С. И. Измерение поперечных размеров летательных аппаратов по частотной протяженности доплеровского портрета // Радиотехника,  2008. № 1.  стр. 84–90.

3.      Митрофанов Д. Г. Комплексный адаптивный метод построения радиолокационных  изображений в системах управления двойного назначения // Теория и системы управления. Известия РАН, 2006. № 1. стр. 101–118.

4.      Митрофанов Д. Г. Метод построения радиолокационных  изображений аэродинамических летательных аппаратов // Полёт, 2006. № 11. стр. 52–60.

5.      Митрофанов Д. Г. Экспериментальные исследования параметров траекторных  нестабильностей   полета   воздушных   объектов.  Воронеж:  НПФ  «САКВОЕЕ» ООО. Сборник докладов XV международной конференции «RLNC-2009», 2009. стр. 1536–1547.

6.     Вентцель Е. С. Теория вероятностей. М.: Наука, 1969, стр. 351-369.

7.     Митрофанов Д. Г. Адаптивный выбор положения интервала синтезирования при наличии у объекта траекторных нестабильностей полета. М.: ООО «Информпресс-94». Труды РНТОРЭС имени А. С. Попова.  13-я Международная конференция DSPA-2011. Цифровая обработка сигналов и ее применение. Выпуск XIII-2. 2011. стр. 37–40.