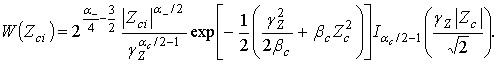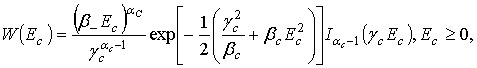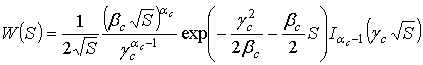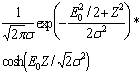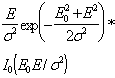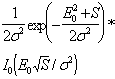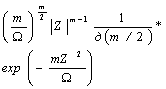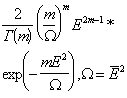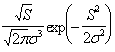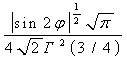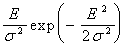УДК 621.396.33
ОБОБЩЕННАЯ МОДЕЛЬ РАДИОЛОКАЦИОННЫХ СТАЦИОНАРНЫХ НЕГАУССОВЫХ СИГНАЛОВ
Н. С. Акиншин 1, Р. П. Быстров 2, В. Л. Румянцев 1
1 ОАО Центральное конструкторское бюро аппаратостроения, г. Тула
2 Институт радиотехники и электроники им. В.А.Котельникова РАН, г. Москва
Получена 29 ноября 2011 г.
Аннотация. Дается теоретическое описание обобщенной вероятностной модели радиолокационных стационарных негауссовых cигналов во временной и частотной области.
Ключевые слова: радиолокационный сигнал, частично-поляризованные компоненты, оценка параметров, вероятностная модель, негауссовский сигнал.
Abstract. The theoretical description of Model probability of radar stationary and periodic- stationary non- gauss signals at time – frequency was obtained.
Keywords: a radar signal, partially polarized components, evaluation of parameters, possibility model, non-Gaussian signal.
1. Введение
Важнейшей задачей при разработке РЛС является определиться, как «наилучшим» образом обработать данные, полученные в результате наблюдений. Известно, что такая процедура зависит от многих факторов. Среди наиболее важных факторов следует указать число состояний сигнала, априорные вероятности этих состояний, возможности правильных и неправильных решений («стоимости»), а также ограничения, налагаемые на процесс получения отсчетов (выборок) самой радиолокационной системой и радиолокационной обстановкой.
Моделирование стоимостных критериев качества может быть довольно сложным, но в основе данного подхода лежит простая модель, которая классически характеризуется в [1] путем минимизации функции стоимости.
Процедура дискретной выборки имеет высокую стоимость в смысле затраты времени на обнаружение. Чем больше объем выборки - при условии, что прочие факторы фиксированы, - тем меньше скорость поиска или скорость (частота) принятия решений радиолокационной системой. Кроме того, сама по себе задержка решения может иметь большую стоимость, - настолько большую, что, в крайнем случае, правильное, но запоздалое решение может достигать стоимости ошибочного решения. Эти потери можно выразить в функции стоимости, суммируя по всем возможным ситуациям с сигналами и решениями и по всем объемам выборок произведения соответствующих стоимостей и вероятностей.
Процедуры обнаружения, основанные на критерии минимизации ожидаемой «стоимости», обычно связаны с вычислением отношений правдоподобия. Отношение правдоподобия также широко встречается в оптимальных процедурах, предназначенных для более простых задач обнаружения, где стоимости ошибок и априорные вероятности либо неизвестны, либо не подходят для данной ситуации.
Основными закономерностями в теории обнаружения и обработки радиолокационных сигналов как непрерывных и дискретных случайных величин используются ряд законов их распределения [2].
Наиболее часто при обработке радиолокационных сигналов применяется, считающийся классическим, нормальный (Гауссов) закон распределения случайной величины. В данной статье предложена обобщенная модель стационарного негаусового сигнала, которая, в отличие от Гауссова закона, путем математического моделирования позволяет рассматривать задачи обнаружения сигналов и помех, которые не являются гауссовыми и которые довольно часто встречаются на практике.
В статье при исследовании и выделения особенностей негауссовых сигналов применена самостоятельная терминология, отличная от терминологии при исследовании на основе закона Гаусса.
Если
предположить, что на вход антенны РЛС поступает аддитивная
смесь полезного
частично поляризационных сигнала ![]() и помехи
и помехи ![]()
uc +n(t) = uc (t) + un (t). (1)
Представляя (1) в виде
суперпозиции двух ортогонально поляризованных компонентов в
произвольном, но
одинаковом для сигнала и помехи, поляризационном базисе, можно записать
[3]
uc +n(t)= x[uc 1(t) + un1 (t)] + x2[uc2(t) + un2 (t)]. (2)
Здесь
Re[uc,ni(t)] = Ec,ni(t)cos[w0t + ac,ni(t)], i = 1,2 (3)
где Eci(t), Eni(t), aci(t), ani(t) - огибающие и фазы ортогонально поляризованных компонентов сигнала и помехи соответственно.
В соответствии с феноменологической моделью, представим наземный объект в виде n отражающих групп блестящих точек [2,5]. Каждая из этих групп, в свою очередь, состоит из j, блестящих точек, одна из которых является доминирующей, то есть обладает большей отражающей способностью, чем каждая из (j - 1) оставшихся точек. Считая, что сигналы, отраженные от k - тых групп являются узкополосными и не зависят от сигналов, отраженных от других групп, запишем ортогонально поляризованные компоненты (3) в виде двойной суммы
Uci(t)=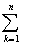
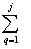 ekqi
cos(w0t + ykqi) , (4)
ekqi
cos(w0t + ykqi) , (4)
где e kqi, y kqi - амплитуда и фаза i-го
ортогонально поляризованного компонента элементарного сигнала,
отраженного от q
- ой блестящей точки k - ой группы. Тогда представляя
(4) в виде квадратурных
составляющих [3]
Uci(t) = xci cosw0 t + yci sin w0t, (5)
Eci = ![]() ,
jci = arctg (yci/xci)
,
(6)
,
jci = arctg (yci/xci)
,
(6)
где
xciI =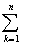 xki, yci
=
xki, yci
=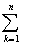 yki,
xki =
yki,
xki = 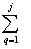 ekqi
cosykqi , yki
=
ekqi
cosykqi , yki
= 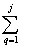 ekqisinykqi
(7)
ekqisinykqi
(7)
запишем мощность ортогонально поляризованных компонентов частично поляризованного сигнала на входе приемной антенны РЛС в виде
Sci = Eci2
= xci2 + yci2
=
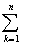 xki
2 +
xki
2 + 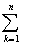 yki2
, i=1,2
.
(8)
yki2
, i=1,2
.
(8)
Учитывая, что ekqi являются проекциями единичных векторов на ортогональные направления x1 и x2 и число складываемых элементарных сигналов j велико, можно считать, что к каждой из сумм по j (7) применима центральная предельная теорема теории вероятностей и распределения случайных величин xki и yki являются нормальными. Степень близости плотности распределения вероятностей (ПРВ) Wi(xk ) и Wi(yk) к нормальным в общем случае зависит от вида ПРВ амплитуд Wi(eq ) и фаз Wi(yq) элементарных сигналов в k-ой группе, а также от числа "блестящих" j - ых точек и может быть оценена на основании известных методов [4].
2. Вероятностная модель стационарного негауссового сигнала
Если предположить, что квадратурные составляющие xki и yki являются независимыми стационарными процессами, с равными дисперсиями sxki2 = syki2 = ski2 и средними значениями xoki и yoki не равными нулю, то есть в соответствии с (7)
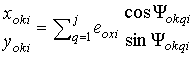 (9)
(9)
где ![]() -
амплитуда и фаза i - го
ортогонально поляризованного компонента элементарного сигнала,
отраженного от
q - ой детерминированной блестящей точки k - ой
группы, то,
учитывая, что сумма квадратов независимых нормальных
случайных величин (8) с
математическим ожиданием не равным нулю, подчиняется
нецентральному
-
амплитуда и фаза i - го
ортогонально поляризованного компонента элементарного сигнала,
отраженного от
q - ой детерминированной блестящей точки k - ой
группы, то,
учитывая, что сумма квадратов независимых нормальных
случайных величин (8) с
математическим ожиданием не равным нулю, подчиняется
нецентральному ![]() - распределению
[4], представим плотность распределения квадратов параметров
- распределению
[4], представим плотность распределения квадратов параметров ![]() и
и ![]() в
виде [2,5]
в
виде [2,5]
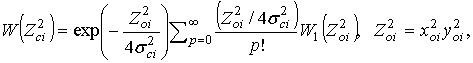 (10)
(10)
где
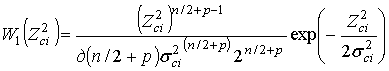 -
(11)
-
(11)
- центральное
( ![]() -
распределение с (n+2p) степенями свободы,
-
распределение с (n+2p) степенями свободы,
![]() - определены
в (9), Г(∙) - гамма-функция.
- определены
в (9), Г(∙) - гамма-функция.
Воспользовавшись соотношением [9] для функции Бесселя от мнимого аргумента n - го порядка
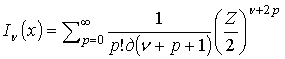 (12)
(12)
свернем сумму по p в (10), а затем, переходя по известным правилам преобразования [3] к квадратурной составляющей Zci получим
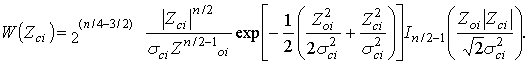 (13)
(13)
Из
(13) следует, что распределения квадратурных составляющих
ортогонально
поляризованных компонентов сигнала ![]() и
и ![]() являются
негауссовыми, следовательно, и
сами ортогонально поляризованные компоненты Uci (t),
определяемые выражением (4), представляют собой негауссовые процессы.
являются
негауссовыми, следовательно, и
сами ортогонально поляризованные компоненты Uci (t),
определяемые выражением (4), представляют собой негауссовые процессы.
Отметим,
что свойства функции (13) не нарушаются, если параметр n
принимает
нецелочисленные значения, то есть ![]() , где
, где ![]() .
.
Введем
новые параметры ![]() тогда из
(13) следует
тогда из
(13) следует
В формуле (14) и ниже индекс i временно опущен.
Определим ПРВ огибающей Eс и
фазы ![]() ортогонально поляризованного компонента рассматриваемого
негауссового сигнала.
Для этого, учитывая независимость квадратурных составляющих,
определим с
учетом (14) их совместное распределение
ортогонально поляризованного компонента рассматриваемого
негауссового сигнала.
Для этого, учитывая независимость квадратурных составляющих,
определим с
учетом (14) их совместное распределение ![]() , а затем
перейдем в нем к новым переменным
, а затем
перейдем в нем к новым переменным
![]()
В результате преобразований получим
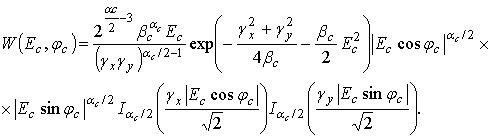 (15)
(15)
Выражение
(15), описывающее совместную ПРВ огибающей и фазы
ортогонально
поляризованного компонента негауссового частично поляризованного
сигнала,
обобщает ранее известные случаи и является исходным для
определения одномерных
ПРВ W(Eс) и W(jс). Интегрируя (15) по
исключающим
переменным и полагая для простоты, что ![]() , получим
соответственно [7,8]
, получим
соответственно [7,8]
![]() (17)
(17)
где
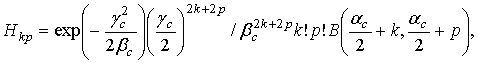
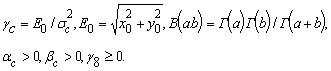
Из
(16) и (17) следует, что огибающая Eс и фаза ![]() являются
статистически
зависимыми, а распределение фазы неравновероятное.
являются
статистически
зависимыми, а распределение фазы неравновероятное.
В
соответствии с рассмотренной феноменологической моделью отраженного
частично
поляризованного негауссового сигнала, можно дать следующую физическую
интерпретацию ![]() ,
,
![]() и
и
![]() .
Параметр
.
Параметр ![]() ,
учитывающий число
отражающих групп объекта, характеризует глубину флуктуаций ортогонально
поляризованных компонент негауссового сигнала; параметр
,
учитывающий число
отражающих групп объекта, характеризует глубину флуктуаций ортогонально
поляризованных компонент негауссового сигнала; параметр ![]() характеризует
отношение
детерминированной составляющей сигнала к его дисперсии, а параметр
характеризует
отношение
детерминированной составляющей сигнала к его дисперсии, а параметр ![]() -
обратно
пропорционален дисперсии.
-
обратно
пропорционален дисперсии.
Для
мощности отраженного сигнала ![]() можно записать [8,10] выражения для
дифференциальной и интегральной функций распределения
можно записать [8,10] выражения для
дифференциальной и интегральной функций распределения
 (19)
(19)
где ![]() интегральная
функция для
центрального
интегральная
функция для
центрального ![]() распределения.
распределения.
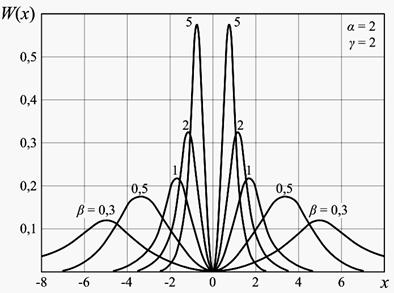
Рисунок 1 - Плотность распределения вероятностей W(x) при α = γ = 2,
β – переменная.
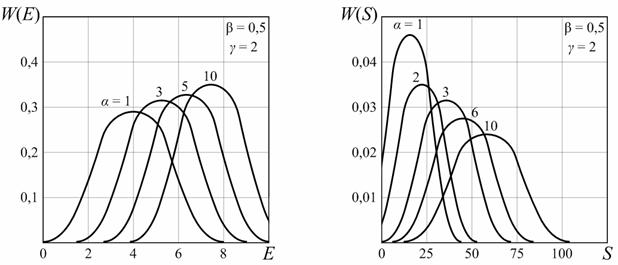
Рисунок 2 - Зависимость плотности распределения вероятностей при переменном значении α и постоянных значениях β = 0,5 и γ = 2,0 и для: а) - W(E); б) -W(S).
На рис. 1 представлены кривые ПРВ квадратурной составляющей сигнала W(x) , а на рис. 2 а и 2 б соответственно кривые для ПРВ W(Е) и W(s) .
Видно,
что кривые W(x) являются двумодальными и симметричными
относительно оси ординат, кривые W(Е) и W(S)
одномодальный характер, причем с увеличением параметра ![]() они
нормализуются. На рис.
3. а,б представлены кривые W(j) [6] для некоторых
значений параметров
они
нормализуются. На рис.
3. а,б представлены кривые W(j) [6] для некоторых
значений параметров ![]() ,
, ![]() и
и ![]() . Из рис. 3.а видно, что при
одинаковом числе компонент в квадратурных составляющих (
. Из рис. 3.а видно, что при
одинаковом числе компонент в квадратурных составляющих (![]() )>1
и
)>1
и ![]() наиболее
вероятные значения фазы
группируются вокруг
наиболее
вероятные значения фазы
группируются вокруг ![]() ,
где n = 0,1,2 . Если (
,
где n = 0,1,2 . Если (![]() )
<1 и
)
<1 и ![]() , то наиболее вероятные значения фазы
возможны
при,
, то наиболее вероятные значения фазы
возможны
при, ![]() и
n
= 0,1,2. Таким образом, кривая W(
и
n
= 0,1,2. Таким образом, кривая W(![]() ) имеет
повторяющийся характер с периодом,
равным
) имеет
повторяющийся характер с периодом,
равным ![]() Результаты
расчета W(
Результаты
расчета W(![]() )
при
)
при ![]() и
и
![]() представлены
на рис. 3.б.
Видно, что при
представлены
на рис. 3.б.
Видно, что при ![]() ,
максимальные значения вероятностной кривой группируются вокруг,
,
максимальные значения вероятностной кривой группируются вокруг, ![]() , n =
0,1,2.
Указанное подчеркивает зависимость структуры фазы от превалирующей
квадратурной
составляющей.
, n =
0,1,2.
Указанное подчеркивает зависимость структуры фазы от превалирующей
квадратурной
составляющей.

а) б)
Рисунок 3 - Зависимости плотности распределения вероятностей W(φ)
при постоянных γ1 = γ2 = 0 и β = 1,0 и для: а) α1 = α2 = var; б) α1 ≠ α2 = var .
Распределение (18) может быть использовано для аппроксимации экспериментальных гистограмм эффективной поверхности рассеяния наземных целей [10-12].
Распределения
(14),(16) - (18) являются базовыми и включают как частные случаи
известные
гауссовые и негауссовые вероятностные модели сигналов. Формульные
зависимости W(Z),
W(E) и W(![]() ) (20) – (24) для частных случаев
обобщенного негауссового распределения представлены в табл. 1.
) (20) – (24) для частных случаев
обобщенного негауссового распределения представлены в табл. 1.
Таблица 1 – Частные случаи обобщенного негауссовского распределения.
|
№ формулы |
W(Z),Z=X,Y
|
W(E), |
|
|
Параметры |
||
|
|
|
|
|||||
|
20 |
|
|
|
|
1 |
|
|
|
21 |
|
|
|
|
|
|
0 |
|
22 |
|
|
|
|
2 |
|
0 |
|
23 |
|
|
|
|
|
|
0 |
|
24 |
|
|
|
|
1 |
|
0 |
Так, в
формуле (20) распределение W(E) (см. табл. 1) совпадает
с
распределением Райса [15], распределение W(S)
является
нецентральным ![]() распределением
с двумя степенями свободы, распределение W(Z)
негауссовое, а
распределение фазы W(
распределением
с двумя степенями свободы, распределение W(Z)
негауссовое, а
распределение фазы W(![]() ) неравновероятно и совпадает с
приведенными в работе [15].
) неравновероятно и совпадает с
приведенными в работе [15].
В (21)
распределение W(E) совпадает с распределением Накагами
[15], ПРВ W(S)
описывается распределением [14], W(Z) имеет негауссовое
распределение и W(![]() ) - неравновероятно. В зависимости (22)
ПРВ
W(E) - однодоминатное плюс релеевское распределение,
распределение W(S) совпадает со второй моделью Сверлинга
[16] , W(Z)
- негауссовое и W(
) - неравновероятно. В зависимости (22)
ПРВ
W(E) - однодоминатное плюс релеевское распределение,
распределение W(S) совпадает со второй моделью Сверлинга
[16] , W(Z)
- негауссовое и W(![]() ) неравновероятно. В (23) подчиняется
распределению
Масквелла-Больцмана [15], W(Z) – негауссовое, а W(
) неравновероятно. В (23) подчиняется
распределению
Масквелла-Больцмана [15], W(Z) – негауссовое, а W(![]() )-
неравновероятно, а в
(24) распределение W(E) - релеевское [18] , W(S)
-
описывается экспоненциальным распределением (первая моделью Сверлинга),
распределение W(
)-
неравновероятно, а в
(24) распределение W(E) - релеевское [18] , W(S)
-
описывается экспоненциальным распределением (первая моделью Сверлинга),
распределение W(![]() ) - равновероятно. Отметим, что если в
(16)
положить
) - равновероятно. Отметим, что если в
(16)
положить
![]() ,
,
то
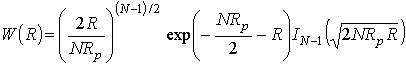 (25)
(25)
подчиняется распределению Маркума [15] , где параметр Rp характеризует отношение максимальной мощности одиночного импульсного сигнала к средней мощности помехи на выходе согласованного фильтра. Распределением (25) можно описывать ПРВ огибающей на выходе квадратичного детектора после накопителя.
Если при определении W(x,y)
и W(![]() ) в
(8) положить
) в
(8) положить ![]() ,
то при выводе выражения для W(Eс) после
нормировки
вида
,
то при выводе выражения для W(Eс) после
нормировки
вида ![]() ,
проделав соответствующие преобразования, получим распределение :
,
проделав соответствующие преобразования, получим распределение :
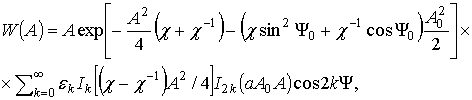
где
![]()
Из
данного распределения при ![]()
![]() следует распределение Бекмана [14]
следует распределение Бекмана [14]

а при ![]() получим
распределение
Хойта [15]
получим
распределение
Хойта [15]
![]() (26)
(26)
Видно, что распределения за исключением последнего сложны и малопригодны для практики в силу громоздкости и невозможности получения в замкнутом виде выражения для анализируемых вероятностных характеристик сигнала.
3 Оценка параметров негауссовой модели
В
работе [18] получены выражения для оценки ![]() начальных
моментов огибающей
начальных
моментов огибающей ![]() и мощности
и мощности ![]() отраженного
сигнала
отраженного
сигнала
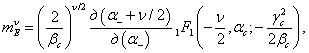 (27)
(27)
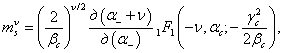 (28)
(28)
где ![]() (a,b,c)
- вырожденная
гипергеометрическая функция.
(a,b,c)
- вырожденная
гипергеометрическая функция.
В
дальнейшем для удобства записи индекс «с» для параметров ![]() и
и ![]() временно
опустим.
временно
опустим.
Для
анализа статистических характеристик мгновенных значений сигнала
ортогонально
поляризованных компонентов (3) при условии ![]() в
работе [20] определены выражения для ПРВ
W(U) и
в
работе [20] определены выражения для ПРВ
W(U) и ![]() начальных
моментов W(U)
начальных
моментов W(U)
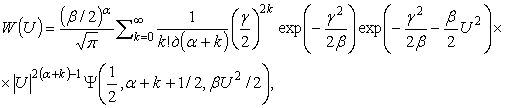 (29)
(29)
где

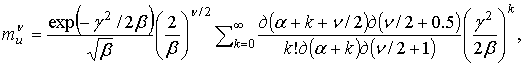 (30)
(30)
где ![]() = 2,4,6...
= 2,4,6...
Положив
в (27) и (30) ![]() =
2 получим
=
2 получим ![]() Откуда
следует, что мощность любого (а не только гауссового) узкополосного
стационарного
случайного сигнала равна половине мощности его огибающей. На основе
(27) - (30)
могут быть определены выражения
Откуда
следует, что мощность любого (а не только гауссового) узкополосного
стационарного
случайного сигнала равна половине мощности его огибающей. На основе
(27) - (30)
могут быть определены выражения ![]() и
и ![]() для
частных случаев, представленных в
табл. 1. Выражение (28) является исходным для оценки параметров
обобщенного
негауссового распределения. Такие оценки приведены в работах [18,
20].
Основной
для их записи являются выражения для оценок кумулянтов [4]
для
частных случаев, представленных в
табл. 1. Выражение (28) является исходным для оценки параметров
обобщенного
негауссового распределения. Такие оценки приведены в работах [18,
20].
Основной
для их записи являются выражения для оценок кумулянтов [4]
![]() (31)
(31)
и кумулянтных
коэффициентов ![]()
Для ![]() имеем
имеем
 (32)
(32)
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
Коэффициенты
![]() связаны
коэффициентами
вариаций Kvs, асимметрии KAS
эксцесса, Kэs
и среднеквадратическим отклонением следующим образом [4]:
связаны
коэффициентами
вариаций Kvs, асимметрии KAS
эксцесса, Kэs
и среднеквадратическим отклонением следующим образом [4]:
![]() (36)
(36)
Важно
отметить, что кумулянтные коэффициенты ![]() описывают
степень отклонения
вероятностного распределения (18) от гауссовского. Это видно из
разложения (18)
в ряд Эджворта [9]
описывают
степень отклонения
вероятностного распределения (18) от гауссовского. Это видно из
разложения (18)
в ряд Эджворта [9]
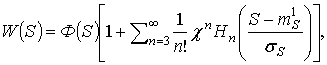 (37)
(37)
где Ф(S) - ПРВ нормального закона; Hn(Z) - полином Эрмита.
Кроме
того, величина ![]()
где
![]() (38)
(38)
характеризует глубину флуктуаций ЭПР цели, которая для моделей Сверлинга [15] не превышает единицу.
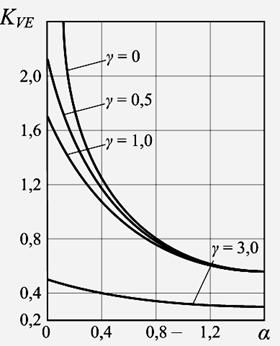
Рисунок 4 –
Зависимость ![]() от параметров α и γ
при β= 1.
от параметров α и γ
при β= 1.
На основе (27) и (36) можно получить выражение для коэффициента вариации огибающей Е сигнала
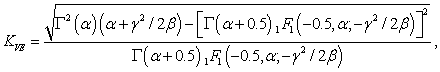 (39)
(39)
по которому рассчитаны
кривые
![]() при
фиксированных значениях
при
фиксированных значениях ![]()
![]() и
и ![]() (см.
рис. 4). Видно, что при
(см.
рис. 4). Видно, что при ![]() асимптотически стремится
к бесконечности. Наиболее интенсивно величина
асимптотически стремится
к бесконечности. Наиболее интенсивно величина ![]() изменяется
при
изменяется
при ![]() ,
а при
,
а при ![]() и
и
![]() ,
,
![]() ,
что подтверждает возможность описания
распределением (16) нерелеевских флуктуаций огибающей отраженного
сигнала.
Оценки параметров
,
что подтверждает возможность описания
распределением (16) нерелеевских флуктуаций огибающей отраженного
сигнала.
Оценки параметров ![]() и
и
![]() можно
найти
из системы уравнений [18,20]
можно
найти
из системы уравнений [18,20]
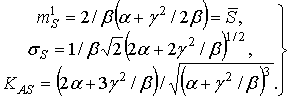 (40)
(40)
Первое
уравнение совпадает с выражением, полученным в [2]. Из первого и
второго при ![]()
![]() и
и ![]() следуют
известные оценки параметров m и
следуют
известные оценки параметров m и ![]() для
гамма - распределения [4,16,17]
для
гамма - распределения [4,16,17]
![]() (41)
(41)
где ![]() выборочное
среднее,
выборочное
среднее, ![]() и
и
![]() -
оценки параметров
-
оценки параметров ![]() и m.
и m.
При
совместном решении системы (40) могут быть получены достаточно общие
оценки
параметров ![]() и
и
![]() которые
будут
иметь следующий вид [20]
которые
будут
иметь следующий вид [20]
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
где ![]()
Отметим,
что вычисление оценок ![]() и
и
![]() может
быть
произведено на основе известных соотношений [6, 13,19]:
может
быть
произведено на основе известных соотношений [6, 13,19]:
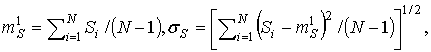 (45)
(45)
![]() ,
(46)
,
(46)
где ![]() выборка
ЭПР объекта; N
- объем выборки.
выборка
ЭПР объекта; N
- объем выборки.
Выражение
для стандартных ошибок оценок параметров ![]() и
и ![]() при
условии, что величины
при
условии, что величины ![]() и
и ![]() некоррелированы
получены в
работе авторов [8,13,20]. Там же показано, что при увеличении объема N
стандартные ошибки стремятся к нулю, причем при N ³ 500 величина
некоррелированы
получены в
работе авторов [8,13,20]. Там же показано, что при увеличении объема N
стандартные ошибки стремятся к нулю, причем при N ³ 500 величина ![]() <
0,3.
<
0,3.![]()

Рисунок 5 - Области обобщенных распределений в системе кривых Пирсона.
Таким
образом, определены достаточно простые выражения оценок параметров
обобщенного
негауссового распределения (18) через физически измеренные
параметры ![]() и
и ![]() , а также выражения для (
, а также выражения для (![]() )
начальных, центральных
моментов и кумулянтных коэффициентов, что позволило построить область
распределения (18) в системе кривых Пирсона (см. рис. 5).
)
начальных, центральных
моментов и кумулянтных коэффициентов, что позволило построить область
распределения (18) в системе кривых Пирсона (см. рис. 5).
При этом оказалось, что область обобщенного распределения охватывает область широкого класса вероятностных моделей, применяемых в статистической радиотехнике. Полученные результаты позволяют использовать синтезированную вероятностную модель на практике для аппроксимации экспериментальных гистограмм ЭПР малоразмерных объектов. Необходимо отметить, что распределение (18) позволяет описывать более глубокие флуктуации ЭПР, чем модели Сверлинга [12].
Представляет
определенный интерес анализ поведения оценок при изменении объема
выборки и
требуемой их точности. Поэтому в [19] получено выражение для ПРВ оценки
параметров ![]() :
:![]()
 (47)
(47)
где
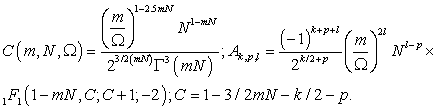
N - объем выборки.
Коэффициент доверия,
связывающий оценку параметра m с заданной относительной
точностью ![]() и величиной N,
имеет вид:
и величиной N,
имеет вид:
![]() (48)
(48)
где 2![]() -
доверительный интервал;
-
доверительный интервал;
 (49)
(49)
Анализ представленных
выражений дает объективную информацию о проведении оценки параметра m,
получаемую еще до проведения измерений на основе априорной информации о
m,![]() ,N.
Кроме того, эти
выражения полезны при анализе асимптотических свойств
,N.
Кроме того, эти
выражения полезны при анализе асимптотических свойств ![]() при
частных значениях параметров
m,
при
частных значениях параметров
m, ![]() ,
N.
,
N.
Таким образом, феноменологический подход при синтезе моделей сигналов, отраженных от объектов, приводит к обобщенной негауссовой модели стационарных сигналов. Первая модель включает, как частные случаи, другие модели (Рэлея, Райса, Хойта, Накагами, однодоминатное плюс релеевское распределение, распределение Максвелла-Больцмана, одностороннее нормальное распределение). Анализ синтезированных вероятностей моделей и статистических характеристик огибающей, мощности и фазы, полученных на основе ПРВ W(E), W(S) и W(j) показывает, что эти модели могут быть использованы для статистического описания частично поляризованных и полностью поляризованных сигналов, у которых флуктуации амплитуд имеют более глубокий характер, чем у релеевской модели, законы распределения фазы многомодальные, а амплитуды и фазы, в общем случае, являются зависимыми между собою случайными величинами.
Литература
1. Справочник по радиолокации. Под ред. М. Сколника. Нью-Йорк,1970. Пер. с англ. (в четырех томах) под общей ред. К.Н. Трофимва. Том 1. Основы радиолокации. Под ред. Я.С.Ицхоки. М.: «Сов. радио». 1976. 456 с.
2. Huynen I., Rivhard H., Mcnolty Frank. Component distribution for fluctuating radar targets // IEEE Trans. Aerospace and Electron. Syst. – 1975. 11. N 6. - p. 1316 1332.
3. Левин Б.Р. Теоретические основы статистической радиотехники, кн. 1. - М.: Сов. радио 1968. 250 с.
4. Крамер Г. Математические методы статистики / Пер. с англ. под ред. А.Н. Колмогорова. М.: Мир. 1975. 648 с.
5. Акиншин Н.С., Мелитицкий В.А., Румянцев В.Л. Среднее число выбросов смеси негауссовского процесса и нормального шума. // Известия вузов МВ и ССО СССР. Радиоэлектроника. 1986. №4. С.25-31.
6. Акиншин Н.С., Мелитицкий В.А., Румянцев В.Л. Некоторые статистические характеристики фазы негауссовского сигнала. // Известия вузов МВ и ССО СССР. Радиоэлектроника. 1986. № 9. С.30-35.
7. Румянцев В.Л., Тормозов А.А., Чесноков Ю.С. Адаптивное радиолокационное обнаружение МНЦ на основе поляризационных различий сигнала и помехи. // Оборонная техника. 1995. №8. С.19-23.
8. Акиншин Н.С., Мелитицкая В.В., Михайлов А.В., Румянцев В.Л. Статистические характеристики отношения смесей гауссова процесса и процесса с негауссовым распределением. // Известия вузов. Радиоэлектроника. 1979. №7. С.52-53.
9. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: ГИФМЛ. 1962. 1097 с.
10. Румянцев В.Л. Адаптивное обнаружение радиолокационных целей по поляризационным параметрам отраженного сигнала. // Оборонная техника. 1995. - №8. С.15-19.
11. Акиншин Н.С., Илюха С.А., Николаев В.А., Румянцев В.Л. Поляризационные характеристики земных покровов при расширенной матрице рассеяния. // Оборонная техника. 1995. №8. С.28-31.
12. Николаев В.А., Румянцев В.Л. Оценка поляризационного состояния сигналов, отраженных от малоразмерных наземных объектов. // Оборонная техника. 1995. №8. С.33-34.
13. Акиншин Н.С., Мелитицкий В.А., Олейник В.А., Румянцев В.Л. Некоторые статистические характеристики параметра m – распределения. // Радиотехника и электроника. 1988. №12. С.8-13.
14. Beckman P., Spizzichino A. The scattering of еlectromagnetic waves from rough surfaces. Oxford, Pergamon Press. 1963.
15. Поздняк С.И., Мелитицкий В.А. Введение в статистическую теорию поляризации радиоволн. М.: Сов. Радио. 1974. 479 с.
16. Хан Г., Шапиро С. Статистические модели в инженерных задачах. - М.: Мир. 1969. 230 с.
17. Тихонов В.И. Выбросы случайных процессов. - М.: Наука, 1970. 392 с.
18. Мелитицкий В.А. Статистические характеристики отношения смесей гауссова процесса и процесса с негауссовым распределением. // Известия вузов. Радиоэлектроника. 1979. №7. С.52-53.
19. Акиншин Н.С., Михайлов А.В., Мелитицкий В.А. Оценка параметров распределения мощности негауссовского сигнала. // Радиотехника и электронника. 1984. №4. С.797-800.
20. Акиншин Н.С., Михайлов А.В., Мелитицкий В.А., Вероятностная модель негауссовского сигнала и ее характеристики // Радиоэлектроника. 1983. №9. С.49-51.