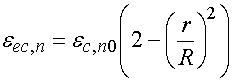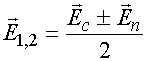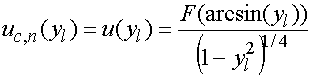УДК 621.396.67
ДВУХСЛОЙНАЯ ПЛАНАРНАЯ ЛИНЗА ЛЮНЕБЕРГА
С. Е. Банков
ИРЭ им. В.А. Котельникова РАН
Получена 3 декабря 2012 г.
Аннотация. Рассмотрена двухслойная планарная линза Люнеберга, обеспечивающая обзор пространства в полном секторе углов 3600 без эффекта затенения облучателями. В рамках теории связанных волн анализируется один из возможных вариантов построения двухслойной линзы, анализируется влияние фазовых искажений, обусловленных наличием двух слоев. Рассматривается реализация двухслойной линзы Люнеберга в виде двух плоских волноводов с неоднородным заполнением, использующих в качестве экранов импедансные пленки, выполненные в виде двумерных индуктивных ленточных решеток. Обсуждаются характеристики устройства.
Ключевые слова: линза Люнеберга, теория связанных волн, плоский волновод, импедансная пленка.
Abstract. Dual layer planar Luneburg lens is considered. The lens provides 3600 scanning sector without effect of shading. One of the possible variant of the lens is analyzes in terms of coupled waves theory. Influence of phase errors caused by presence of two layers is analyzed. Dual layer Luneburg lens in the form of two parallel plate waveguides with non – uniform dielectric filling and impedance films as screens is considered. Two dimensional metal strip arrays are used as impedance films. Parameters of the device are discussed.
Keywords: Luneburg lens, coupled waves theory, parallel plate waveguide, impedance film.
Постановка задачи
Линзы Люнеберга на основе неоднородных сред известны в антенной технике весьма давно [1]. Они привлекают внимание благодаря уникальной возможности обзора пространства в полном секторе азимутальных углов и углов места без уменьшения коэффициента направленного действия (КНД), обусловленного отклонением луча от некоторого направления. Двумерные или планарные линзы Люнеберга [2] потенциально обеспечивают обзор пространства в полном секторе азимутальных углов.
Интерес к линзам Люнеберга обусловлен также проблемами технического освоения миллиметрового и субмиллиметрового диапазонов (ММД и СММД), в которых волноводный принцип пространственной обработки полей, нашедший применение в более низкочастотных диапазонах уступает место квазиоптическим принципам, в которых линзы и зеркала играют определяющую роль. При этом требование технологичности, предъявляемое к устройствам ММД и СММД определяет интерес к линзам, которые могут быть изготовлены методами технологии печатных схем, то есть к двумерным, планарным линзам.
Следует отметить, что основное достоинство линз Люнеберга весьма непросто реализовать на практике вследствие эффекта затенения. Нетрудно увидеть, что размещение облучателей линзы (далее мы будем говорить только о планарных линзах Люнеберга) вдоль всей ее образующей неизбежно приводит к тому, что сформированный одним из них луч искажается облучателями, расположенными на противоположной стороне линзы. В результате сканирование без эффекта затенения допустимо только в секторе углов 900.
В данной работе рассматривается вариант построения линзы Люнеберга, в котором снимается проблема затенения и который увеличивает сектор обзора до 3600. Указанный положительный эффект достигается за счет использования двухслойной конструкции, которая схематично показана на рис. 1.
Линза состоит из двух планарных волноводов (ПЛВ). Они могут иметь различную конструкцию, например, их можно выполнить в виде плоских волноводов (ПВ), планарных диэлектрических волноводов (ПЛДВ) и т.д. Важно, что их эффективная диэлектрическая проницаемость меняется от центра линзы к ее образующей по закону, который обеспечивает преобразование цилиндрической волны облучателя в плоскую волну на выходе линзы.
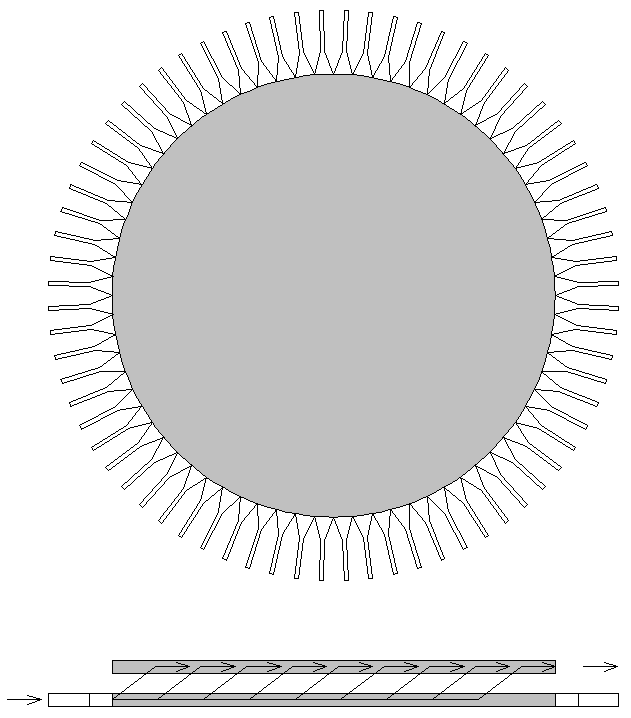
Рис. 1. Структурная схема двухслойной линзы Люнеберга
Также существенным фактором служит распределенная связь ПЛВ. Благодаря этой связи волна по мере распространения вдоль нижнего слоя постепенно переходит на верхний слой свободный от облучателей. Задачей проектирования такой линзы является определение не только закона изменения эффективной диэлектрической проницаемости (ЭДП) ПЛВ, но и закона распределения линейного коэффициента связи (ЛКС) между ПЛВ. К выбору ЛКС предъявляется требование полной перекачки мощности волны, сформированной облучателем на верхний слой линзы.
Нетрудно увидеть, что излучение в свободное пространство происходит с верхнего слоя, минуя облучатели. Таким образом, негативное влияние эффекта затенения устраняется.
В данной работе рассматривается простейший вариант выполнения двухслойной линзы, который будет описан ниже. Он не обеспечивает идеального выполнения требований фазовой коррекции волны и полной перекачки ее мощности на верхний слой. Тем не менее, далее будет показано, что снижение коэффициента направленного действия (КНД), обусловленное указанными погрешностями весьма мало и предлагаемая линза может использовать в практических приложениях. Отметим также, что в апертурных антеннах, к которым относится анализируемая линза, в качестве параметра, характеризующего ее эффективность часто используют, так называемый, коэффициент использования поверхности (КИП).
Исследование двухслойной линзы включает следующие этапы:
1. Исследование в рамках теории связанных волн. На этом этапе мы зададим законы распределения ЭДП и ЛКС и решим задачу об определении амплитудно – фазового распределения поля на выходе линзы, которое формируется точечным источником, расположенным на ее образующей. По найденному распределению мы найдем потери мощности, обусловленные неполной перекачкой энергии на верхний слой и потери КНД, обусловленные неидеальностью сформированного распределения поля.
2. На следующем этапе мы рассмотрим возможную реализацию линзы в виде двух связанных ПВ. Особенностью этих ПВ служит то, что их экраны выполнены в виде двумерных ленточных решеток. Параметры решеток могут меняться в плоскости линзы. Благодаря этому появляется возможность выполнения заданных на первом этапе законов изменения ЭДП и ЛКС. Также мы рассмотрим линзу с неоднородным заполнением ПВ.
1. Структура двухслойной линзы Люнеберга
Будем рассматривать линзу
с одинаковыми ПЛВ. Благодаря этому структура имеет плоскость симметрии. Из
теории связанных волн следует [3], что в симметричной структуре могут
распространяться две основные волны, которые принято называть четной и
нечетной. Четная волна соответствует размещению в плоскости симметрии
магнитной, а нечетная волна электрической стенки. Эти волны имеют разные
постоянные распространения ![]() и
и ![]() . Через них определяется упоминавшийся ЛКС
. Через них определяется упоминавшийся ЛКС
![]() :
:
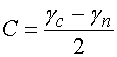 . (1)
. (1)
Особенностью двухслойной
линзы является то, что она описывается двумя ЭДП ![]() и
и ![]() , которые связаны с постоянными
, которые связаны с постоянными ![]() и
и ![]() :
:
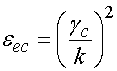 , (2)
, (2)
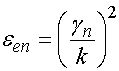 ,
,
где ![]() -
волновое число свободного пространства.
-
волновое число свободного пространства.
В общем случае задача
синтеза двухслойной линзы Люнеберга состоит в определении двух функций ![]() , исходя из сформулированных выше требований.
, исходя из сформулированных выше требований.
Мы упростим задачу, предполагая, что ЛКС является малым параметром:
 . (3)
. (3)
В этом случае можно предположить, что искомые распределения ЭДП для четной и нечетной волн близки к известному решению для однослойной линзы [4]:
где ![]() -
параметры, которые необходимо определить ниже,
-
параметры, которые необходимо определить ниже, ![]() -
радиус линзы. Из формул (4) видно, что принятые законы изменения ЭДП
обеспечивают идеальную фокусировку как четных, так и нечетных волн,
сформированных точечным источником при условии, что внешняя среда для четных
волн имеет ЭДП равную
-
радиус линзы. Из формул (4) видно, что принятые законы изменения ЭДП
обеспечивают идеальную фокусировку как четных, так и нечетных волн,
сформированных точечным источником при условии, что внешняя среда для четных
волн имеет ЭДП равную ![]() , а для нечетных
, а для нечетных ![]() . В тоже время, с практической точки
зрения внешняя среда должна иметь проницаемость равную единице, так как задачей
линзы является излучение в свободное пространство. Отличие
. В тоже время, с практической точки
зрения внешняя среда должна иметь проницаемость равную единице, так как задачей
линзы является излучение в свободное пространство. Отличие ![]() от единицы является источником фазовых
искажений распределения поля в выходной плоскости.
от единицы является источником фазовых
искажений распределения поля в выходной плоскости.
Из соотношений (4) видно, что ЛКС в нашем приближении задан следующей функцией:
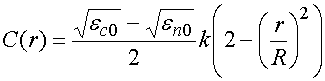 . (5)
. (5)
Таким образом, для
удовлетворения требований к фазовому распределению и потерям мощности мы имеем
два свободных параметра ![]() .
.
2. Анализ линзы Люнеберга с помощью теории связанных волн
Четная и нечетная волны в системе связанных ПЛВ являются ортогональными волнами, распространяющимися независимо друг от друга.
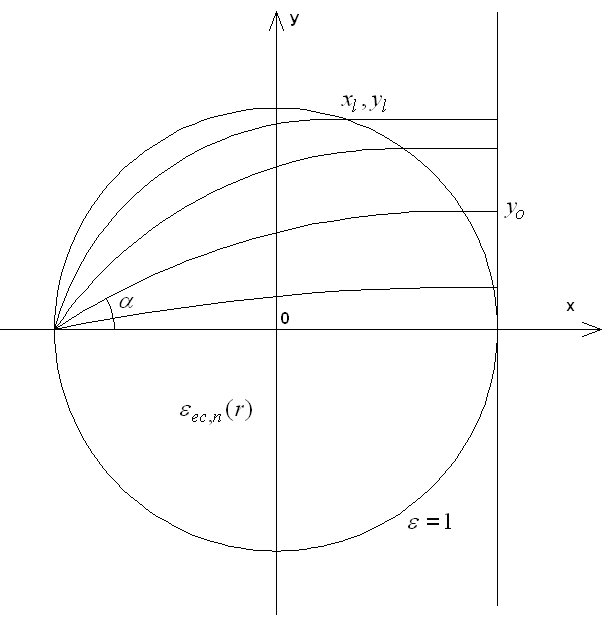
Рис. 2. Лучевая структура поля в линзе Люнеберга
Связь между ними возникает на границах ПЛВ, то есть
в точке возбуждения, которая для определенности будет расположена при ![]() (см. рис. 2) и в точках выхода лучей из
линзы.
(см. рис. 2) и в точках выхода лучей из
линзы.
Внутри линзы при ![]() распространение волн происходит
независимым образом. Источник возбуждения находится на нижнем слое. Опишем его
с помощью диаграммы направленности
распространение волн происходит
независимым образом. Источник возбуждения находится на нижнем слое. Опишем его
с помощью диаграммы направленности ![]() , где
, где ![]() угол, который отсчитывается от оси 0х,
как показано на рис. 2. В рамках теории связанных волн поле в нижнем волноводе,
которому присвоим индекс 1 и в верхнем волноводе с индексом 2, связано с полями
четной и нечетной волн следующим образом:
угол, который отсчитывается от оси 0х,
как показано на рис. 2. В рамках теории связанных волн поле в нижнем волноводе,
которому присвоим индекс 1 и в верхнем волноводе с индексом 2, связано с полями
четной и нечетной волн следующим образом:
где ![]() вектор
электрического поля в нижнем и верхнем ПЛВ, а
вектор
электрического поля в нижнем и верхнем ПЛВ, а ![]() - поля
четных и нечетных волн. Поскольку в точке возбуждения поле в верхнем волноводе
равно нулю, то источник можно описать двумя одинаковыми ДН для четных и
нечетных волн
- поля
четных и нечетных волн. Поскольку в точке возбуждения поле в верхнем волноводе
равно нулю, то источник можно описать двумя одинаковыми ДН для четных и
нечетных волн ![]() :
:
![]() . (7)
. (7)
Из соотношений (6) и (7) видно, что при таком выборе ДН поле в верхнем волноводе в точке возбуждения действительно равно нулю.
Прохождение четных и нечетных волн через линзу будем описывать в приближении геометрической оптики. Траектории лучей внутри линзы известны [4]. Они задаются следующим уравнением:
![]() . (8)
. (8)
Координаты точек на выходе
линзы ![]() записываются следующим образом:
записываются следующим образом:
![]() , (9)
, (9)
![]() .
.
Отметим, что траектории лучей, соответствующие четным и нечетным волнам внутри линзы одинаковы, так как законы изменения ЭДП (4) у них одинаковые.
На выходной поверхности линзы имеется преломление лучей. В однослойной линзе это преломление отсутствует, так как у нее ЭДП на границе равна единице. В нашем случае она немного отличается в силу соотношений (4). Поэтому для определения траекторий лучей нам необходимо оценить величину эффекта преломления. Для этого найдем фазовое распределение поля на поверхности линзы.
Данную задачу нетрудно
решить, исходя из того, что законы изменения ЭДП (4) обеспечивают формирование
волн с идеальным плоским фронтом в линзах, окруженных средами с ЭДП равными ![]() . С учетом этого фактора получаем:
. С учетом этого фактора получаем:
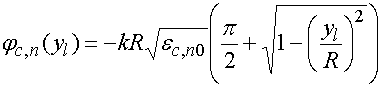 . (10)
. (10)
Для определения фазового
распределения поля в верхнем ПЛВ на выходе линзы нам недостаточно знать фазы
четных и нечетных волн (10). Нам потребуются также их амплитуды. Функция
соответствия, задающая связь между координатой точки ![]() и
углом
и
углом ![]() определена соотношениями (9). Тогда,
воспользовавшись известным соотношением, являющимся выражением закона
сохранения энергии [4], получаем выражения для амплитуд четной и нечетной волн
определена соотношениями (9). Тогда,
воспользовавшись известным соотношением, являющимся выражением закона
сохранения энергии [4], получаем выражения для амплитуд четной и нечетной волн ![]() :
:
Из формул (11) следует, что
амплитудные распределения обеих волн совпадают. Далее воспользуемся
соотношениями (6) и найдем распределение поля в верхнем волноводе ![]() :
:
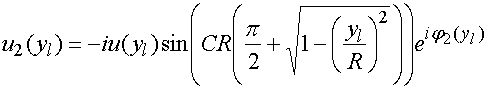 (12)
(12)
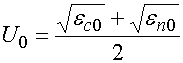 . (13)
. (13)
 . (14)
. (14)
Определяемая выражением (14)
фаза позволяет найти компоненту волнового вектора ![]() касательную
к поверхности линзы (см. рис. 3):
касательную
к поверхности линзы (см. рис. 3):
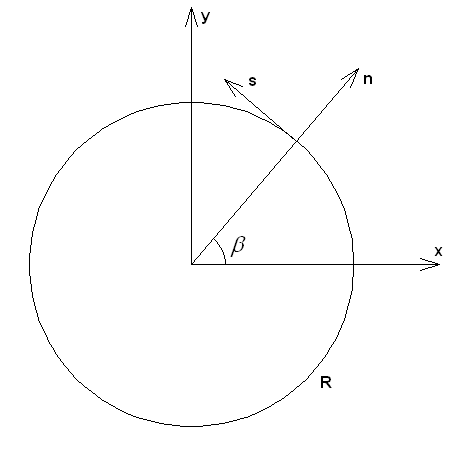
Рис. 3. Определение компонент волнового вектора
 . (15)
. (15)
Координата ![]() связана с длиной дуги окружности
связана с длиной дуги окружности ![]() , отсчитываемой от точки
, отсчитываемой от точки ![]() ,
, ![]() следующим
образом:
следующим
образом:
![]() . (16)
. (16)
С помощью формул (14) – (16) находим:
 . (17)
. (17)
Компонента волнового вектора
для луча вне линзы ![]() записывается следующим образом:
записывается следующим образом:
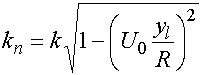 . (18)
. (18)
Компоненты волнового вектора в системе координат XOY находятся с помощью формул (17) и (18):
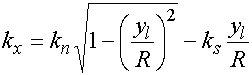 (19)
(19)
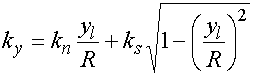
Можно показать, что при
параметре ![]() равном единице компонента
равном единице компонента ![]() равна
нулю. Таким образом, чтобы оценить отклонение лучей от оси 0х нам необходимо
оценить величину параметра
равна
нулю. Таким образом, чтобы оценить отклонение лучей от оси 0х нам необходимо
оценить величину параметра ![]() . Ниже будет показано,
что величина
. Ниже будет показано,
что величина ![]() отличается от единицы не более чем на
одну сотую. Расчеты с помощью формулы (19) показывают, что влияние эффекта
преломления лучей на границе линзы на фазу поля в плоскости
отличается от единицы не более чем на
одну сотую. Расчеты с помощью формулы (19) показывают, что влияние эффекта
преломления лучей на границе линзы на фазу поля в плоскости ![]() при таких значениях параметра
при таких значениях параметра ![]() пренебрежимо мало. Это дает нам основание
считать лучи вне линзы Люнеберга параллельными оси 0х. Отметим, что это
предположение неверно для координат
пренебрежимо мало. Это дает нам основание
считать лучи вне линзы Люнеберга параллельными оси 0х. Отметим, что это
предположение неверно для координат ![]() близких к
близких к ![]() . Однако, эти участки линзы вносят
пренебрежимо малый вклад в формирование поля излучения, так как амплитуда поля
на краях линзы весьма мала при правильном выборе ДН облучателя.
. Однако, эти участки линзы вносят
пренебрежимо малый вклад в формирование поля излучения, так как амплитуда поля
на краях линзы весьма мала при правильном выборе ДН облучателя.
С учетом сделанных выше
замечаний, мы можем записать выражение для распределения поля в плоскости ![]() в верхнем и нижнем волноводах:
в верхнем и нижнем волноводах:
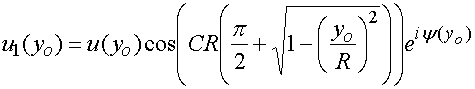 (20)
(20)
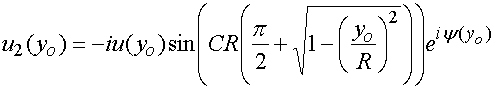
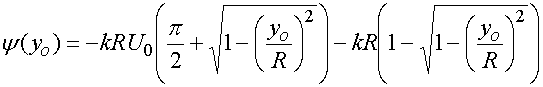
![]() .
.
Знание амплитудно – фазового распределения поля
на излучающей поверхности позволяет найти параметр, характеризующий эффективность
ее КИП ![]() :
:
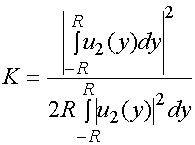 . (21)
. (21)
Относительные потери
мощности ![]() , связанные с неполной передачей энергии в
верхний волновод, записываются следующим образом:
, связанные с неполной передачей энергии в
верхний волновод, записываются следующим образом:
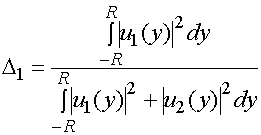 . (22)
. (22)
Также имеются потери ![]() , обусловленные тем, что часть мощности,
излученная источником, не попадает в линзу:
, обусловленные тем, что часть мощности,
излученная источником, не попадает в линзу:
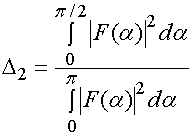 . (23)
. (23)
КПД анализируемого
устройства ![]() связан с потерями
связан с потерями ![]() :
:
![]() . (23)
. (23)
Для характеристики фазового
распределения в выходной плоскости удобно ввести параметр ![]() :
:
![]() . (24)
. (24)
Для исследования
амплитудного распределения нам необходимо задаться ДН облучателя. Выберем ее в
виде ДН апертуры размером ![]() , в которой равномерно
распределены элементы Гюйгенса:
, в которой равномерно
распределены элементы Гюйгенса:
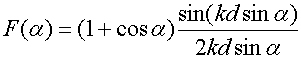 . (25)
. (25)
Рассмотрим далее зависимость
характеристик линзы Люнеберга от параметров ![]() и
и ![]() :
:
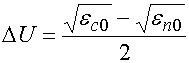 . (26)
. (26)
На рис. 4 и 5 показаны
типичные примеры распределения амплитуд и фаз в выходной плоскости ![]() . Кривые на рис. 4 и 5 получены при
. Кривые на рис. 4 и 5 получены при ![]() ,
, ![]() ,
, ![]() . Кривые 1 – 3 на рис. 4 соответствуют
. Кривые 1 – 3 на рис. 4 соответствуют ![]() .
Видно, что фазовая ошибка на выходе линзы существенно зависит от величины
.
Видно, что фазовая ошибка на выходе линзы существенно зависит от величины ![]() и быстро растет с ростом ее отличия от единицы.
и быстро растет с ростом ее отличия от единицы.
Амплитудное распределение определяется преимущественно формой ДН облучателя. При этом следует отметить всплески на краях линзы, обусловленные структурой лучей (см. формулу (11)).
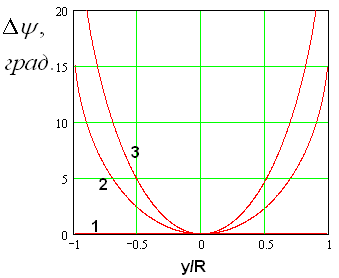
Рис. 4. Фазовое распределение на выходе линзы
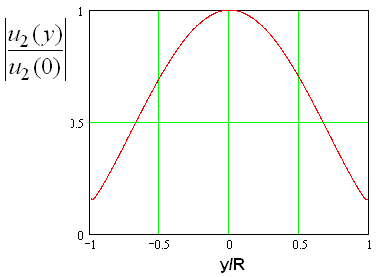
Рис. 5. Амплитудное распределение на
выходе линзы при ![]()
На рис. 6 представлено амплитудное распределение, полученное для меньшего
размера облучателя ![]() . Видно, что распределение ближе
к равномерному, а всплески на краях заметны отчетливее, чем на рис. 5.
. Видно, что распределение ближе
к равномерному, а всплески на краях заметны отчетливее, чем на рис. 5.
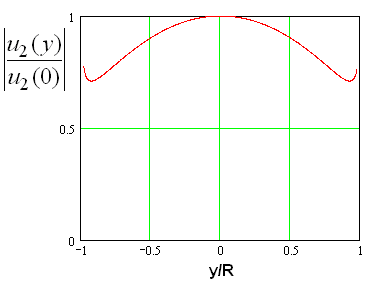
Рис. 6. Амплитудное распределение на
выходе линзы при ![]()
Параметр 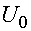 на амплитудное распределение
влияет весьма слабо. Преимущественно от него зависит распределение фазы.
на амплитудное распределение
влияет весьма слабо. Преимущественно от него зависит распределение фазы.
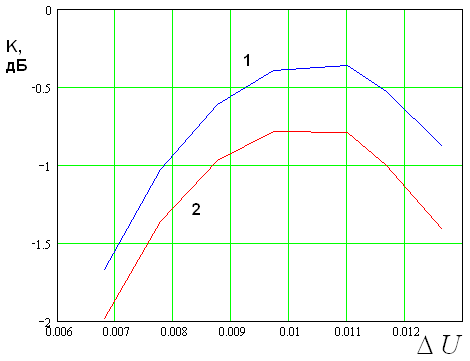
Рис. 7. Зависимость КИП от параметра ![]()
На рис. 7 показана зависимость КИП от параметра  , определяющего связь между ПЛВ. Кривые
1,2 получены при
, определяющего связь между ПЛВ. Кривые
1,2 получены при 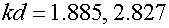 соответственно и
соответственно и 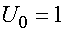 . Видно, что кривые имеют экстремум
примерно при
. Видно, что кривые имеют экстремум
примерно при 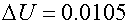 . При этом облучатель меньшего
размера обеспечивает более высокий КИП. Отметим, что при этом в силу известных
из теории антенн закономерностей [5], уровень боковых лепестков в ДН линзы
также будет выше.
. При этом облучатель меньшего
размера обеспечивает более высокий КИП. Отметим, что при этом в силу известных
из теории антенн закономерностей [5], уровень боковых лепестков в ДН линзы
также будет выше.
Следует также отметить, что потери ![]() , связанные с неполной передачей энергии в
верхний волновод в рассматриваемом варианте линзы составляют вблизи
оптимального значения
, связанные с неполной передачей энергии в
верхний волновод в рассматриваемом варианте линзы составляют вблизи
оптимального значения ![]() весьма незначительную величину
около 0.1 дБ.
весьма незначительную величину
около 0.1 дБ.
Таким образом, мы можем сделать вывод, что анализируемая линза может использоваться как антенна с достаточно высокой эффективностью, несмотря на то, что задачи формирования амплитудного и фазового распределений она решает неидеально. Тем не менее, влияние погрешностей на ее функционирование с практической точки зрения незначительно.
3. Двухслойная линза Люнеберга на связанных ПВ
В данном разделе мы рассмотрим практическую реализацию двухслойной линзы Люнеберга в виде связанных ПВ. Она показана на рис. 8. Обычно под ПВ понимают структуру, образованную двумя плоскими металлическими экранами. Особенностью нашего случая является то, что в качестве экранов мы используем полупрозрачные пленки, описываемые импедансными граничными условиями [6]. Такие пленки могут выполняться разными способами. Чаще всего они имеют вид двумерных решеток из лент или щелей в металлическом экране [7]. Также они могут выполняться в виде тонко диэлектрического слоя с высокой проницаемостью [8].
Сейчас для нас способ выполнения импедансной пленки не имеет принципиального значения, поскольку в данном разделе мы решаем задачу определения требуемых значений импедансов, которые обеспечивают выполнение законов изменения ЭДП (4).

Рис. 8. Двухслойная линза Люнеберга на связанных ПВ
Отметим, что с помощью
импедансных пленок можно не только связывать ПВ, но изменять ЭДП четных и
нечетных волн. Импеданс пленки, разделяющей ПВ ![]() преимущественно
определяет связь между волноводами, а импеданс пленок на внешних поверхностях
ПВ
преимущественно
определяет связь между волноводами, а импеданс пленок на внешних поверхностях
ПВ ![]() влияет на ЭДП. Отметим также, что далеко
не все значения импедансов могут быть реализованы на практике. Поэтому мы
оставляем возможность изменения ЭДП за счет заполнения ПВ средой с переменной
диэлектрической проницаемостью
влияет на ЭДП. Отметим также, что далеко
не все значения импедансов могут быть реализованы на практике. Поэтому мы
оставляем возможность изменения ЭДП за счет заполнения ПВ средой с переменной
диэлектрической проницаемостью ![]() .
.
Отметим также, что мы
рассматриваем исключительно пленки без тепловых потерь, поэтому они имеют чисто
мнимые комплексные импедансы ![]() .
.
Анализ собственных волн
связанных ПВ с импедансными пленками будем проводить стандартным путем,
записывая поля в частичных областях и удовлетворяя затем условиям на границах
ПВ. Нас интересуют Е – волны с компонентами ![]() (см.
рис. 9).
(см.
рис. 9).
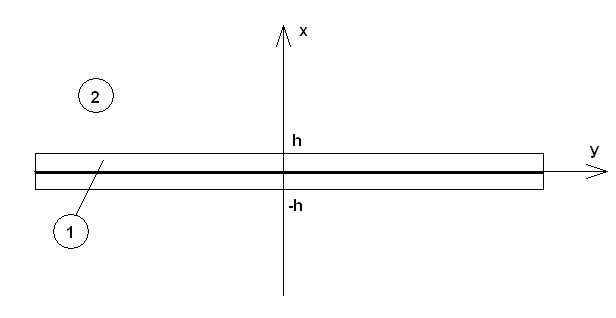
Рис. 9. Связанные ПВ
Структура на рис. 9 симметрична относительно плоскости YOZ. Поэтому при анализе четных волн мы можем разместить в ней магнитную стенку, а при анализе нечетных волн электрическую [9].
Граничные условия на импедансной пленке имеют следующий вид:
![]() , (27)
, (27)
![]() ,
,
знак плюс в формулах (27) соответствует полю на верхней поверхности пленки, а минус на нижней.
Опуская подробности решения граничной задачи, приведем окончательный результат в виде дисперсионных уравнений для четных и нечетных волн соответственно:
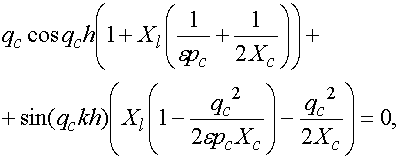 (26)
(26)
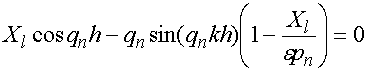 , (27)
, (27)
![]() ,
,
![]() ,
,
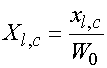 ,
,
![]() -
волновое сопротивление свободного пространства.
-
волновое сопротивление свободного пространства.
Уравнение (26) соответствует четным волнам, а (27) нечетным. Обычно их решают относительно ЭДП. Нас интересуют значения импедансов. Их можно аналитически найти из соотношений (26) и (27) в явном виде:
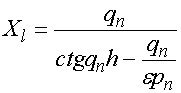 , (28)
, (28)
 . (29)
. (29)
В формулах (28), (29) мы
полагаем, что ЭДП ![]() заданы законами (4). Далее
рассмотрим несколько численных примеров. В первом из них считаем, что диэлектрическая
проницаемость ПВ равна единице. В этом случае формирование ЭДП полностью
происходит за счет изменения импедансов.
заданы законами (4). Далее
рассмотрим несколько численных примеров. В первом из них считаем, что диэлектрическая
проницаемость ПВ равна единице. В этом случае формирование ЭДП полностью
происходит за счет изменения импедансов.
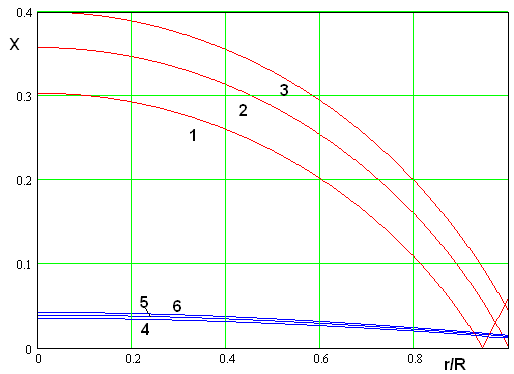
Рис. 10. Зависимость импеданса от
радиальной координаты при ![]()
На рис. 10 показана зависимость
импеданса от нормированной радиальной координаты. Кривые получены при ![]() мм,
мм, ![]() ГГц,
ГГц, ![]() . Кривые 1 – 3 соответствуют параметру
. Кривые 1 – 3 соответствуют параметру ![]() и
и ![]() , а
кривые 4 – 6 параметру
, а
кривые 4 – 6 параметру ![]() при тех же значениях
при тех же значениях ![]() .
.
Следует обратить внимание на то, что
реализация значений ![]() меньших единицы (см. кривую 1)
требует смены знака импеданса
меньших единицы (см. кривую 1)
требует смены знака импеданса ![]() вблизи границы линзы.
Наоборот, при
вблизи границы линзы.
Наоборот, при ![]() импеданс знака не меняет и
остается везде индуктивным. Точное равенство импеданса нулю на границе линзы
достигается при
импеданс знака не меняет и
остается везде индуктивным. Точное равенство импеданса нулю на границе линзы
достигается при ![]() . Отметим, что при этом величина
. Отметим, что при этом величина
![]() не равна единице и, следовательно, линза
имеет фазовые искажения (см раздел 2). Устранить эти искажения в
рассматриваемой конструкции весьма непросто, так как создание малого по
величине емкостного импеданса с помощью печатных решеток затруднительно.
не равна единице и, следовательно, линза
имеет фазовые искажения (см раздел 2). Устранить эти искажения в
рассматриваемой конструкции весьма непросто, так как создание малого по
величине емкостного импеданса с помощью печатных решеток затруднительно.
Обращает на себя внимание
также то, что по абсолютной величине импеданс ![]() намного
превышает
намного
превышает ![]() , по крайней мере, в центральной части
линзы. Отметим, что выполнение больших индуктивных импедансов с помощью
ленточных решеток также представляет сложную технологическую задачу. Поэтому
имеет смысл рассматривать также линзу с неоднородным диэлектрическим
заполнением:
, по крайней мере, в центральной части
линзы. Отметим, что выполнение больших индуктивных импедансов с помощью
ленточных решеток также представляет сложную технологическую задачу. Поэтому
имеет смысл рассматривать также линзу с неоднородным диэлектрическим
заполнением:
В этом случае импеданс ![]() практически не отличается от нуля, а
зависимость импеданса
практически не отличается от нуля, а
зависимость импеданса ![]() от нормированного радиуса
показана на рис. 11. Кривая получена при
от нормированного радиуса
показана на рис. 11. Кривая получена при ![]() .
Остальные параметры структуры приведены выше.
.
Остальные параметры структуры приведены выше.
Компромиссным решением может
служить частичное заполнение ПВ в области ![]() однородным
диэлектриком с проницаемостью
однородным
диэлектриком с проницаемостью ![]() . На рис. 12 показана
зависимость импеданса от радиуса при
. На рис. 12 показана
зависимость импеданса от радиуса при ![]() =1.5 и
=1.5 и ![]() . Кривая 1 соответствует
. Кривая 1 соответствует ![]() , а кривая 2 импедансу
, а кривая 2 импедансу ![]() . Видно, что теперь максимальное значение
импеданса стало меньше, чем на рис. 10.
. Видно, что теперь максимальное значение
импеданса стало меньше, чем на рис. 10.
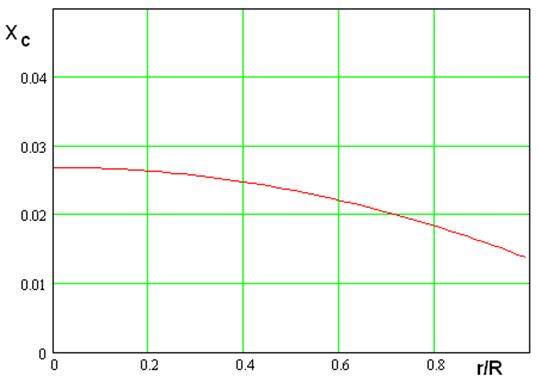
Рис. 11. Зависимость импеданса от радиальной координаты при переменной диэлектрической проницаемости
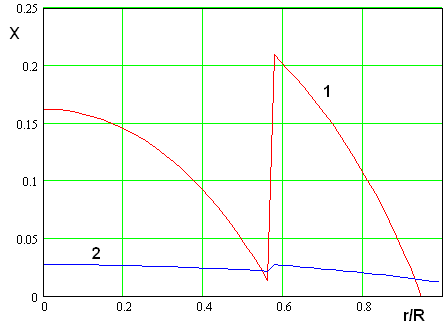
Рис. 12. Зависимость импеданса от радиальной координаты при частичном заполнении ПВ
4. Реализация импедансных пленок в виде двумерных ленточных решеток
Наиболее полно теория двумерных ленточных решеток
представлена в работе [10]. Из нее можно получить зависимость импеданса ![]() от периода решетки
от периода решетки ![]() и коэффициента заполнения
и коэффициента заполнения ![]() , равного отношению ширины ленты
, равного отношению ширины ленты ![]() к периоду:
к периоду:
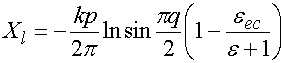 (31)
(31)
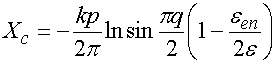
Отметим сразу, что из соотношений (31) видно, что
вариант с воздушным заполнением ПВ практически нереализуем, поскольку в центре
линзы при ![]() множители в скобках близки к нулю.
множители в скобках близки к нулю.
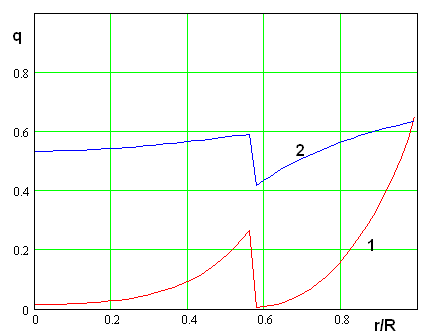
Рис. 13. Зависимость коэффициента заполнения решетки от радиуса для линзы с частичным заполнением ПВ
Поэтому выполнить пленки с
конечными значениями импедансов можно только за счет уменьшения параметра ![]() до нуля. Однако это невозможно в силу
технологических ограничений на ширину лент.
до нуля. Однако это невозможно в силу
технологических ограничений на ширину лент.
Вариант с частичным
заполнением более реален. На рис. 13 показана зависимость коэффициента
заполнения от радиуса. Кривые 1 и 2 получены при ![]() мм,
мм, ![]() ГГц,
ГГц, ![]() ,
, ![]() ,
, ![]() мм,
мм, ![]() =1.5 и
=1.5 и ![]() и
соответствуют импедансам
и
соответствуют импедансам ![]() и
и ![]() .
.
С технологической точки
зрения наиболее приемлем вариант с переменным диэлектрическим заполнением по
закону (30). Зависимость коэффициента заполнения решетки, реализующей импеданс ![]() , полученная для параметров приведенных
выше показана на рис. 14.
, полученная для параметров приведенных
выше показана на рис. 14.
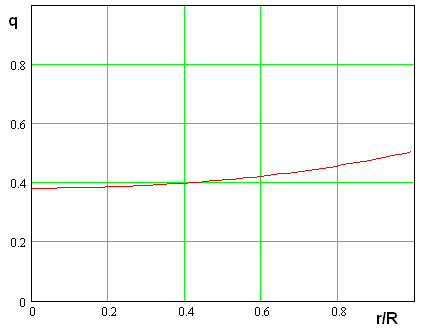
Рис. 14. Зависимость коэффициента заполнения решетки от радиуса для линзы с переменной диэлектрической проницаемостью
Из рис. 14 видно, что коэффициент заполнения близок к 0.5. Выполнение решетки с таким отношением ширины ленты к периоду не должно вызывать технологических сложностей.
Работа выполнена при поддержке Российского фонда фундаментальных исследований, проект № 12-08-12003/12 офи_м.
Литература
1. Luneburg R.K. The mathematical theory of optics. University of California press. 1964.
2. Зелкин Е. Г., Петрова Р. А. Линзовые антенны. М.: Сов. радио, 1974.
3. Унгер Г.Г. Планарные и волоконные оптические волноводы. М.: Мир, 1980.
4. Корнблит С. СВЧ оптика. М.: «Связь». 1980.
5. Сазонов Д.М. Антенны и устройства СВЧ. М.: Высш. Шк. 1998.
6. Курушин Е.П., Нефедов Е.И. Электродинамика анизотропных волноведущих структур. М.: Наука. 1983.
7. Нефедов Б.И., Сивов А.Н Название: Электродинамика периодических структур. М.: Наука. 1977.
8. Вайнштейн Л.А. Теория диффракции и метод факторизации. М.: Сов. Радио. 1966.
9. Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. М.: Радио и связь. 1983.
10. Конторович М.И., Астрахан М.И., Акимов В.П., Ферсман Г.А. Электродинамика сетчатых структур. М.: Радио и связь. 1987.