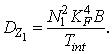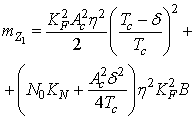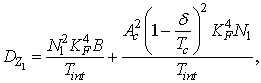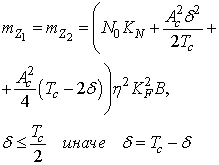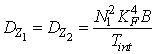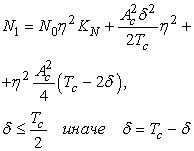УДК 621.396.621.59

поиск ПО ЗАДЕРЖКЕ СИГНАЛА С минимальной частотной модуляциЕЙ И ПРЯМЫМ РАСШИРЕНИЕМ СПЕКТРА

 

М. Ю. Баланов, А. А. Парамонов

Московский государственный технический университет радиотехники электроники и автоматики

 

Получена 12 ноября 2012 г.

 

Аннотация: В работе рассматривается проблема поиска широкополосного сигнала на фоне шумовых помех. Широкополосный сигнал получается путем прямого расширения спектра узкополосного сигнала с минимальной частотной модуляцией. Выполнен статистический анализ обнаружителя широкополосного сигнала. На основе полученных соотношений определены численные оценки вероятностей пропуска сигнала и ложной тревоги.

Ключевые слова: широкополосные сигналы, поиск, синхронизация, энергетический обнаружитель, вероятность ложной тревоги, вероятность пропуска.

Abstract: A problem of search algorithm for spread spectrum signal is considered in the paper. The spread spectrum signal is direct spread of minimum frequency shift keying (MSK) signal. The probability analysis of spread spectrum search detector is performed. Using obtained equations the estimation of missing and alarm probabilities are calculated.

Key words: spread spectrum signal, search algorithm, synchronization, energy detector, alarm probability, missing probability.

 

Активное использование широкополосных сигналов в системах связи, навигации и управления [1-3] требует детальной проработки и анализа алгоритмов приема таких сигналов. При этом необходимо учитывать, что на вход приемного устройства наряду с полезным сигналом может поступать мощная шумовая помеха, превосходящая по мощности сигнал в несколько раз. Наиболее сложным в этих условиях является начальный этап работы системы связи – этап установления соединения. На этом этапе информация о реальных параметрах принимаемого сигнала минимальна и главной задачей является обеспечение синхронизации приемника по параметрам принимаемого широкополосного сигнала. Наиболее важным из них является сдвиг по времени расширяющей псевдослучайной последовательности (ПСП) в приемнике относительно ПСП в передаваемом сигнале. Его определение связано с поиском сигнала по всей зоне неопределенности этого параметра.

В работе рассматривается проблема поиска по задержке широкополосного сигнала (ШПС) с прямым расширением спектра узкополосного сигнала с минимальной частотной модуляцией (МЧМ). Рассматриваются модификации алгоритма принятия решения о наличии сигнала с целью улучшения работы алгоритма поиска в условиях априорной неопределенности относительно параметров принимаемых сигналов.

На вход приемного устройства поступает смесь полезного сигнала и шума:

.                                                                                                    (1)

Полезным является широкополосный сигнал, сформированный путем прямого расширения спектра сигнала МЧМ путем его модуляции псевдослучайной последовательностью (ПСП)  с элементами :

.                                                                                       (2)

Здесь  – несущая частота полезного сигнала;  – начальная фаза сигнала в момент времени ;  – фаза сигнала, несущая информационное сообщение.

Функция корреляции расширяющего сигнала в идеальном случае имеет вид

                                                                                            (3)

Эта корреляционная функция представлена на рис. 1. Она будет использоваться в дальнейшем при анализе. Влияние неидеальности корреляционной функции ПСП ниже рассмотрено отдельно.

 

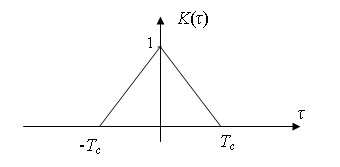
Рис. 1. Корреляционная функция идеального расширяющего сигнала

 

При вычислении корреляционной функции полезного принимаемого сигнала (2) можно принять, что исходный сигнал МЧМ является гармоническим (это допущение тем точнее, чем больше коэффициент расширения спектра):

 

Входящий в (1) гауссовский шум  имеет равномерный в полосе  спектр:

                                                      

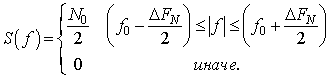
Корреляционная функция шума:

   

                             

Структурная схема обнаружителя широкополосного сигнала представлена на рис. 2 [1].

 

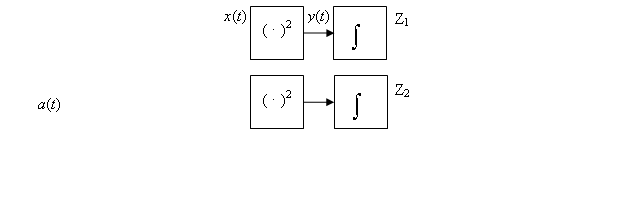
Рис. 2. Схема обнаружителя широкополосного сигнала.

 

В перемножитель на входе схемы подаются принимаемое колебание r(t) и видеоимпульсы, соответствующие символам исходной ПСП , от управляемого генератора ПСП. При идеальной синхронизации генератора ПСП эта операция должна привести к снятию с сигнала МЧМ расширяющей последовательности, при неидеальной – в сигнале полностью или частично остается фазовая манипуляция по псевдослучайному закону. Получившийся сигнал МЧМ с центральной частотой спектра f₀ проходит через основной канал, т.е. через верхнюю ветвь схемы (полосовой фильтр с полосой пропускания B – квадратичный детектор – сумматор). Нижняя ветвь – боковой канал – подобна верхней, но полосовой фильтр в ней настроен на частоту, отличную от частоты сигнала. Назначение этой ветви – измерение уровня шума. Необходимость бокового канала объясняется тем, что уровень шума на входе приемника может существенно меняться, но система автоматической регулировки усиления приемника поддерживает стабильным уровень входного процесса (сигнал плюс шум). Это значит, что за счет действия системы АРУ меняется уровень сигнальной части процесса r(t). С  учетом этого при принятии решения алгоритм поиска может основываться не только на анализе уровня сигнала, а также на определении соотношения мощностей сигнала и шума в принимаемом колебании. Квадратичное детектирование и интегрирование процессов в основном и боковом каналах позволяет получить оценки мощностей процессов в этих каналах, которые используются для вынесения решения о наличии сигнала в данной ячейке зоны неопределенности длительностью T_c. Решение о наличии сигнала может приниматься на основе разных критериев. В момент принятия решения отсчёт напряжения z на выходе вычислителя сравнивается с пороговым значением z_th. Если z>z_th, то считается, что данная временная ячейка содержит полезный сигнал. Если z<z_th, то считается, что ячейка содержит только шум и поиск продолжается на следующем интервале области неопределенности.

В момент начала просмотра ячейки зоны неопределенности опорный сигнал имеет расстройку относительно принимаемого сигнала Δ=kT_c +δ, где 0≤δ<1– расстройка в пределах одного символа ПСП, k – количество символов ПСП (целое число), на которое расстроен опорный сигнал.

Поступающее в обнаружитель (рис. 2) колебание (1) перемножается с опорным сигналом:

.

 

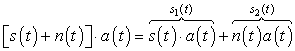Сигнал s₁(t) имеет две составляющие – регулярную и случайную (рис. 3).

 

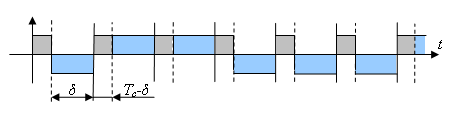
Рис.3. Структура сигнала s₁(t). Вертикальные сплошные линии – границы тактовых интервалов ПСП в принимаемом сигнале, пунктирные линии – границы тактовых интервалов генерируемой в обнаружителе ПСП. Серая заливка – регулярная составляющая, голубая заливка – случайная составляющая. В областях выше оси абсцисс s₁(t) = s(t), а ниже оси абсцисс s₁(t) = –s(t).

 

Регулярная составляющая имеет место лишь при k=0, т.е. только в том случае, когда расхождение по времени между ПСП, присутствующей в сигнале, и ПСП на выходе генератора не превышает T_c . В этом случае регулярная составляющая представляет последовательность фрагментов восстановленного исходного сигнала (2) с нулевой начальной фазой. Длительность каждого фрагмента составляет T_c-δ, а период повторения – T_c . Поскольку после перемножителя в схеме стоит полосовой фильтр, он выделит сигнал, но амплитуда его будет:

,                                                      

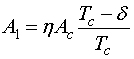где  – некоторый несущественный коэффициент.

При нулевой расстройке (δ = 0) амплитуда первой гармоники максимальна, а случайная составляющая отсутствует.

Случайная составляющая представляет собой последовательность фрагментов исходного сигнала (2) с начальной фазой, случайным образом принимающей значения 0 или p. Длительность этих фрагментов составляет δ, а период повторения – T_c.

При k=0 случайная составляющая имеет следующую корреляционную функцию:

                                 

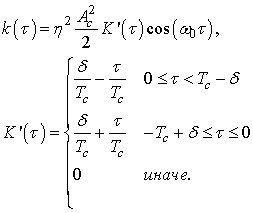
Спектральная плотность мощности случайной составляющей при k=0:

.                    

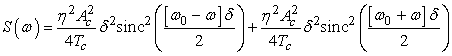Если ω=ω₀, то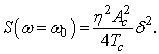                                      

При k≠0 в сигнале s₁(t) имеется только случайная составляющая. Рассмотрим случай  (в ином случае необходимо поменять местами  и ).

Корреляционная функция случайной составляющей на выходе перемножителя:

                                  

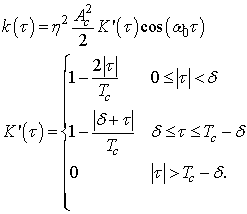
По корреляционной функции можно найти энергетический спектр случайной составляющей; в области центральной частоты  спектральная плотность мощности постоянна, т.е. в полосе пропускания ПФ случайная составляющая представляет собой белый шум:

     

                        

Корреляционная функция шумовой составляющей s₂(t) определяется как произведение корреляционных функций процесса n(t) и опорной ПСП :

                

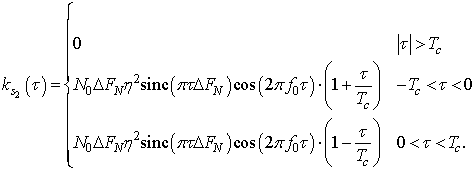
По этой корреляционной функции находится спектральная плотность мощности шумовой составляющей, значение которой в области центральной частоты постоянно, т.е. в полосе пропускания ПФ шум является белым:

                      

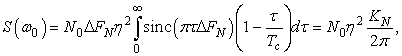
где

 

В формулу входит некоторый коэффициент . Расчеты показывают, что для большинства реальных ситуаций этот коэффициент близок к единице.

Итак, на ПФ поступает полезный сигнал с амплитудой 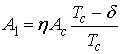 при 0≤δ<1 и белый гауссовский шум со спектральной плотностью мощности N₁:

,                                                                                                    (4)

где

                                               

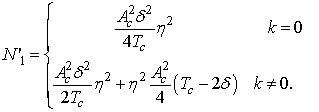
Полосовые фильтры имеют коэффициент передачи по напряжению K_F на центральной частоте и полосу пропускания B, в пределах которой частотная характеристика постоянна. На выходе полосового фильтра основного канала имеем сумму полезного сигнала с амплитудой A₂= K_F A₁ и помехи в виде БГШ со спектральной плотностью мощности в полосе частот фильтра .

                               

где .

На выходе квадратичного детектора выделяется сигнал

                                          (5)

 

После прохождения через квадратичный детектор сигнал усредняется в интеграторе в течение времени T_int >> T_c:

        

                                        

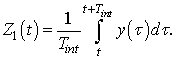
При большой постоянной времени  распределение величины  может считаться нормальным.

Поскольку решение о наличии начала ПСП в некоторой ячейке зоны неопределенности принимается на основе вычисленных значений  и , необходимо знать статистические характеристики этих величин. Вычисления проведем для основного канала, т.е. для величины ; формулы для статистических характеристик величины  выводятся аналогично. Они приведены ниже.

Математическое ожидание сигнала на выходе интегратора:

а) при наличии сигнала (k=0)

                  

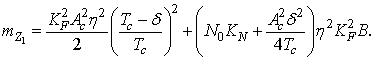
б) при отсутствии сигнала (k≠0)

     

Если на вход квадратичного детектора поступает лишь гауссовский шум (регулярной составляющей нет) со спектральной плотностью (4), то, используя [6], можно вычислить энергетический спектр сигнала на его выходе:

  

                            

Интегратор имеет частотную характеристику .

 

Соответственно, на выходе интегратора имеем спектральную плотность мощности

 

            

 

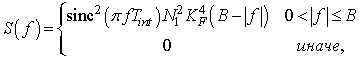
проинтегрировав которую, получим дисперсию процесса Z₁:

                                                                                           (6)

Отбрасывание в подынтегральном выражении (6) сомножителя в скобках дает несколько завышенное значение интеграла, но позволяет получить компактное выражение для дисперсии:

                                                (7)

Определим дисперсию сигнала Z₁ на выходе интегратора для случая наличия сигнала (k = 0).

С учетом (5) ковариационная функция сигнала y(t) на выходе устройства возведения в квадрат имеет вид:

                         (8)

где

  –

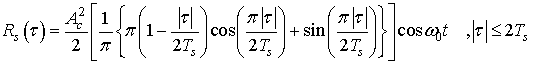 корреляционная функция сигнала МЧМ. Она получается из известного выражения для спектра комплексной огибающей этого сигнала [5]:

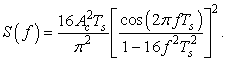
В (8) входит величина  – тактовый интервал сигнала МЧМ и ковариационная функция шума, полученная в [6]:

 

После подстановки корреляционных функций сигнала и шума на входе устройства возведения в квадрат получаем:

                        

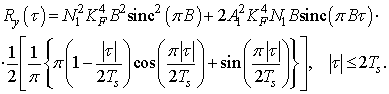
Дисперсия величины Z₁:

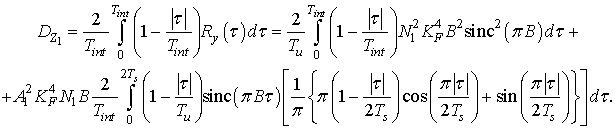
Здесь в последнем интеграле изменены пределы интегрирования, так как корреляционная функция полезного сигнала принимает ненулевые значения только в пределах интервала [-2T_s, 2T_s].

При выполнении условия  первое слагаемое в последнем выражении приводится к виду (7). Интеграл во втором слагаемом близок к значению B/2 (численное интегрирование это подтверждает), поэтому:

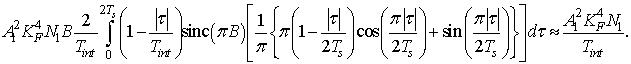
В результате выражение для дисперсии величины Z₁ существенно упрощается:

                                       

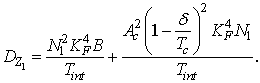
Итак, получены статистические характеристики независимых гауссовских величин и . Они сведены в таблицу. 

 

	Математическое ожидание	Дисперсия
Основной канал, наличие сигнала (k=0)
Боковой канал, наличие сигнала (k=0)
Основной канал, боковой канал, отсутствие сигнала (k≠0)		,

 

При практической реализации обнаружителя необходимо знать, при какой задержке δ достигается (в среднем) максимальное напряжение на выходах основного и бокового каналов в отсутствие и при наличии сигнала. Исследование на экстремум математических ожиданий  и  по задержкам показывает, что в отсутствие синхронизма () их максимальные значения достигаются при δT_c=0. Кстати, в этом случае максимальной оказывается и дисперсия величин  и . При наличии синхронизма (k=0) наихудший случай наступает при задержке, равной половине тактового интервала ПСП δT_c=1/2. Учет наихудшего и наилучшего случая необходим при определении вероятностей ложной тревоги и пропуска сигнала.

Поиск целесообразно осуществлять последовательным просмотром временных ячеек длительностью по 0.5T_c. Тогда минимальное значение математических ожиданий  и  при (k=0) будет наблюдаться при расстройке δ=0.25T_c, то есть половина шага поиска.

Приведенные в таблице формулы выведены для случая, когда расширяющая спектр ПСП имеет идеальную автокорреляционную функцию (3). В действительности, автокорреляционная функция имеет боковые пики, которые следует учесть как источник дополнительных составляющих энергии полезного сигнала в основном канале.

Будем считать, что ПСП  есть повторяющаяся М-последовательность. Как известно, у периодической автокорреляционной функции М-последовательности боковые пики имеют постоянное значение 1/М, где М – период повторения символов ПСП. Соответственно, боковые пики периодической автокорреляционной функции равны 1/ M .

Наличие боковых пиков периодической автокорреляционной функции приводит к тому, что часть энергии полезного сигнала при k≠0 все же просачивается в основной канал, что может привести к ложному захвату сигнала по боковому лепестку автокорреляционной функции. Поэтому такая ситуация должна быть исключена или, по крайней мере, ее вероятность должна быть минимизирована настолько, насколько это возможно. С этой целью время интегрирования следует выбирать в целых периодах повторения ПСП Т_int=lMT_c (l = 1, 2, 3…). В этом случае будет обеспечиваться минимальное просачивание сигнала в основной канал. В противном случае, при других временах интегрирования, не гарантируется цельность периода повторения ПСП и, как результат, возможно большее просачивание сигнала в основной канал за счет больших боковых пиков автокорреляционной функции.

С учетом просачивания бокового лепестка периодической автокорреляционной функции сигнал основного канала будет иметь следующие характеристики (k≠0):

                

 

                                    

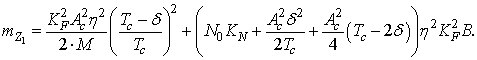
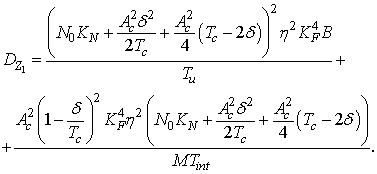
Обнаружитель, структура которого приведена на рис. 2, выносит решение о наличии начала ПСП в той или иной временной ячейке зоны неопределенности на основании сравнения некоторой вычисляемой им величины z с порогом z_th. Согласно [6], в качестве такой величины может быть использована:

- энергия сигнала на выходе основного канала;

- разность между энергиями сигнала в основном и боковом каналах ;

При выборе порога z_th следует руководствоваться следующим: порог не должен быть слишком высоким, чтобы обнаружить с требуемой вероятностью оцениваемый временной сдвиг ПСП, и, вместе с тем, он не должен быть низким, чтобы не происходила ложная синхронизация по боковым пикам автокорреляционной функции ПСП или по шумам.

Определим вероятности этих двух событий, учтя, что Z₁ и Z₂ – независимые гауссовские величины с параметрами, приведенными выше в таблице. При выборе способа вычисления величины z и порога будем ориентироваться на наихудший случай. Для определенности примем время интегрирования равным l – целому числу периодов ПСП Т_int=lMT_c. Наихудшими случаями будут являться в отсутствие сигнала (k≠0) нулевая задержка опорного сигнала относительно принимаемого (δ=0) и в случае наличия сигнала (k=0) задержка опорного сигнала относительно принимаемого на время δ=0.25T_c.

Результаты расчета математического ожидания в зависимости от отношения сигнал/шум на входе приемника приведены на рис.4 для случая частоты выдачи символов ПСП 15 МГц. Далее все расчеты проводились для следующих условий:   M=1023, B = 30 кГц, К_N = 1, частота манипуляции МЧМ 16 кГц, мощность шума измеряется в полосе 35 МГц (при частоте ПСП 15 МГц) или 3,5 МГц (при частоте ПСП 1,5 МГц), l=10 (частота ПСП 15 МГц) или l=1 (частота ПСП 1,5 МГц) – так чтобы общее время поиска было одинаково для различных частот ПСП. Учтено также наличие в приемнике системы автоматической регулировки усиления, поддерживающей постоянный уровень напряжения (сигнал плюс помеха) на входе обнаружителя, равный 0,1 В.

 

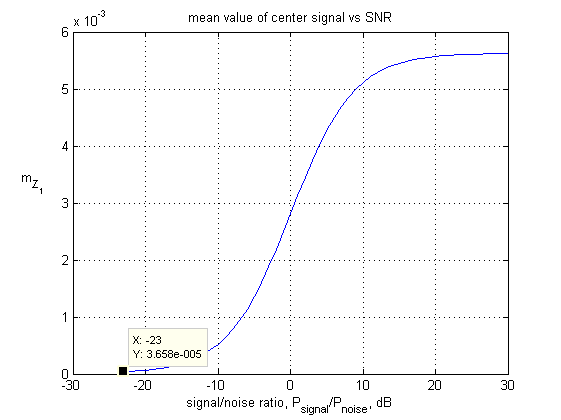
Рис.4 Среднее значение сигнала интегратора основного канала для наихудшего случая (k=0, δ=0.25), T_c = 1/(15·10⁶) c.

 

Зависимость математического ожидания  от отношения сигнал/шум имеет прозрачное физическое объяснение, если принять во внимание наличие системы АРУ. При малых отношениях сигнал/шум доля шума значительна и до значений порядка -10 дБ математическое ожидание меняется слабо. Далее сигнал начинает превосходить шум, и математическое ожидание монотонно растет с ростом отношения сигнал/шум. При дальнейшем увеличении этого отношения мощность шума становится пренебрежимо малой, а рост математического ожидания прекращается в связи с тем, что напряжение сигнала стабилизируется системой АРУ. Интересным для нас является значение математического ожидания при самом низком допустимом отношении сигнал/шум. Пороговое значение в устройстве поиска должно устанавливаться ниже этого минимального значения математического ожидания. Например, если минимальное отношение сигнал/шум равно -20 дБ, то порог разумно выбрать равным -23дБ с учетом запаса на различные погрешности реализации обнаружителя.

На рис. 5 показаны следующие характеристики сигналов в порядке их упоминания в легенде сверху вниз: 1) математическое ожидание сигнала на выходе бокового канала при наличии сигнала; 2) среднеквадратичное отклонение сигнала основного канала при наличии сигнала; 3) среднеквадратичное отклонение сигнала бокового канала при наличии сигнала; 4) среднее значение сигнала основного канала при отсутствии синхронизма; 5) среднеквадратичное значение сигнала основного канала при отсутствии синхронизма; 6) среднее значение сигнала основного канала при отсутствии синхронизма, но с учетом утечки сигнала за счет бокового лепестка автокорреляционной функции; 7) среднеквадратическое отклонение сигнала основного канала при отсутствии синхронизма, но с учетом утечки сигнала за счет бокового лепестка автокорреляционной функции. Эти параметры рассчитаны для тех же исходных данных, для которых построен рис.4.

 

Рис. 5 Статистические характеристики сигнала на выходе интегратора,  T_c = 1/(15·10⁶) с.

 

Как видно из приведенных данных, наиболее опасным явлением при поиске является утечка сигнала в основной канал с учетом значений пиков боковых лепестков корреляционной функции. Математическое ожидание такого сигнала при больших отношениях сигнал/шум близко к математическому ожиданию сигнала в основном канале при малых отношения сигнал/шум, что может привести к ситуации ложного захвата сильного полезного сигнала по боковому лепестку автокорреляционной функции.

На рис. 6 и рис.7 приведены аналогичные данные, но для тактовой частоты символов ПСП, равной 1.5 МГц. Математическое ожидание сигнала в основном канале для данного режима совпадает с математическим ожиданием сигнала в основном канале для режима 15 МГц. Это и не удивительно, потому что в основной канал попадает большая мощность полезного сигнала, а уровень шума незначителен.

 

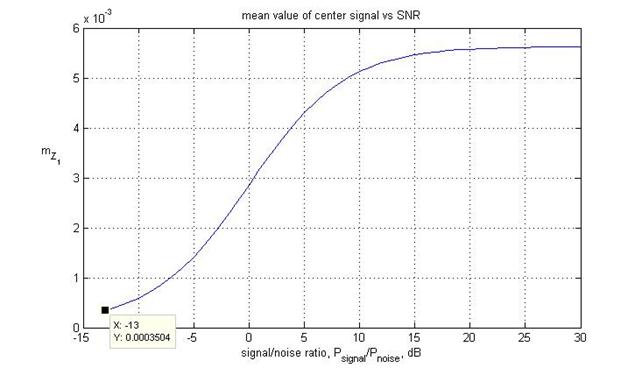
Рис. 6. Среднее значение сигнала Z₁ на выходе интегратора основного

канала для наихудшего случая (k=0, δ=0.25), T_c = 1/(15·10⁵) c.

 

Заметные различия в характеристиках сигналов для различных режимов работы видны из сравнения рис. 5 и рис. 7. Видно, что для режима 1.5 МГц уровень среднеквадратического отклонения уменьшается, а зависимость среднеквадратического отклонения от отношения сигнал/шум менее заметна. Исходя из приведенных данных, можно сделать вывод о том, что поиск сигнала в режиме 1.5 МГц может быть осуществлен быстрее и надежнее, чем для режима 15 МГц.

 

Рис. 7. Статистические характеристики сигналов Z₁ и Z₂ на выходах

 интеграторов, T_c = 1/(15·10⁵) c.

 

Значения математических ожиданий и дисперсии позволяют определить вероятности ложного захвата и пропуска сигнала с учетом сделанного выше вывода о гауссовском распределении вероятностей сигнала на выходе интегратора. То, что сигнал на выходе интегратора имеет распределение, близкое к нормальному, подтверждается экспериментальными данными согласно методике [7].

Вероятность ложного захвата сигнала определяется как 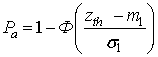, а вероятность пропуска сигнала – как ,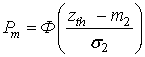

 

где:  – интеграл вероятностей;

 

z_th – порог, с которым сравнивается величина z  при принятии решения о наличии или отсутствии сигнала;

m₁ и σ₁ – математическое ожидание и дисперсия величины z в наихудшем случае отсутствия сигнала;

m₂ и σ₂ – математическое ожидание и дисперсия величины z в наихудшем случае наличия сигнала.

Напомним, что наихудшими являются случай минимального математического ожидания величины z при наличии сигнала (k=0) и максимального математического ожидания величины z при его отсутствии (k≠0). При отсутствии сигнала математическое ожидание рассчитывается с учетом просачивания части сигнала в основной канал. Результаты расчетов вероятности ложного захвата и пропуска сигнала в режиме 15 МГц при различных пороговых уровнях представлены на рис. 8, а для режима 1.5 МГц – на рис. 9.

 

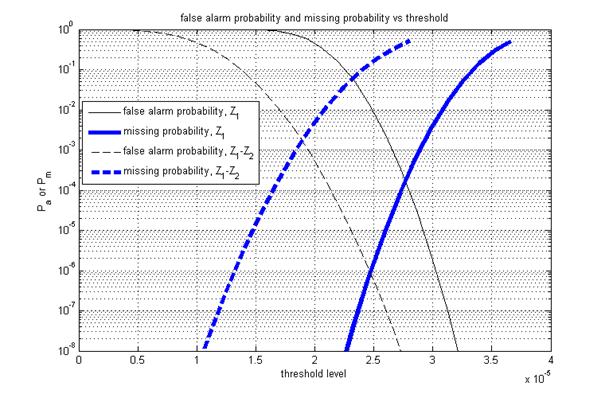
Рис. 8 Вероятности ложной тревоги и пропуска сигнала для режима 15 МГц

 

Зависимости, приведенные на рис. 8 и рис. 9, построены для двух случаев: решение о наличии начала ПСП в той или иной временной ячейке зоны неопределенности выносится по результатам сравнения с порогом величин  и . Для периода повторения ПСП M элементов и поиска сигнала со скачком 1/2T_c в зоне неопределенности сигнала присутствуют (2M-1) зон с отсутствующим сигналом. Каждая из указанных зон должна быть просмотрена. Поскольку поиск сигнала осуществляется случайным образом, то начальное положение фаз принимаемого и опорного сигналов будет случайным и случайным будет положение начальной ячейки зоны неопределенности относительно ячейки с сигналом. В среднем до ячейки с сигналом необходимо просмотреть (2M-1)/2 временных ячеек с отсутствующим сигналом. Для определенности примем, что M=1023, что при просмотре одной пустой ячейки вероятность ложной тревоги должна быть 0.01 и что вероятность пропуска сигнала также равна 0.01. Тогда вероятность ложной тревоги при просмотре всех пустых ячеек зоны неопределенности в среднем должна быть на уровне 10^-5.

Рассмотрим качество работы обоих алгоритмов при двух частотах ПСП. Согласно рис. 8 и рис 9, для режима 15 МГц и критерия  при вероятности пропуска сигнала 0.01 вероятность ложной тревоги будет на уровне 3·10^-7, что меньше требуемого значения 10^-5. Для режима 1.5 МГц при вероятности пропуска сигнала 0.01 вероятность ложного захвата будет намного меньше величины 10^-8. Таким образом, для обеих частот ПСП данный критерий обеспечивает требуемую вероятность ложной тревоги, хотя по этому показателю при фиксированной вероятности пропуска сигнала режим 1.5 МГц все же имеет преимущество перед режимом 15 МГц.

Для режима 15 МГц и критерия  вероятность ложного захвата превышает требуемые нам значения: при вероятности пропуска сигнала 0.01 вероятность ложной тревоги составляет 2·10^-4, что больше установленной нами величины 10^-5. Для режима 1.5 МГц вероятность ложной тревоги ниже величины 10^-8 . Невыполнение требований по вероятности ложной тревоги в режиме 15 МГц означает, что цикл поиска придется повторять несколько раз, т.е. время поиска будет увеличено по сравнению с режимом 1.5 МГц.

 

Рис. 9 Вероятности ложной тревоги и пропуска сигнала для режима 1.5 МГц

 

Литература

1.     Варакин Л.Е. Системы связи с шумоподобными сигналами. – М.: Радио и связь. – 1984. – 384 с.

2.     Помехозащищенность систем радиосвязи с расширением спектра сигналов модуляцией несущей псевдослучайной последовательностью. // В.И. Борисов В.М. Зинчук, А.Е. Лимарев, Н.П. Мухин, Г.С. Нахмансон; Под. Ред В.И. Борисова. – М.: Радио и связь, 2003. – 640 с.

3.     Журавлев В.И. Поиск и синхронизация  в широкополосных системах. – М.: Радио и связь, 1986. – 240 с.

4.     Синхронизация в радиосвязи и радионавигации: Учебное пособие / Б.И. Шахтарин, А.А.Иванов, П.И. Кобылкина, М.А.Рязанова, А.А.Самохвалов, Ю.А.Сидоркина, А.А.Тимофеев. – М.: Гелиос АРВ, 2007. – 256 с.

5.     Банкет В.Л., Дорофеев В.М. Цифровые методы в спутниковой связи. – М.: Радио и связь, 1988. – 240 с.

6.     Шахтарин Б.И. Случайные процессы в радиотехнике. Том 2. Нелинейные преобразования. – М.: ГелиосАРВ, 2006.

7.     ГОСТ Р ИСО 5479-2002. Статистические методы. Проверка отклонения распределения вероятностей от нормального распределения.