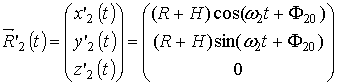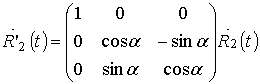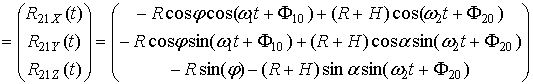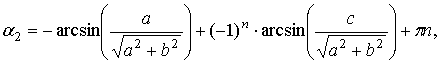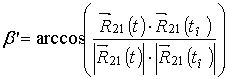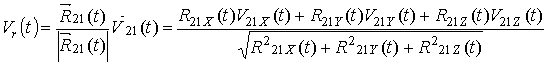Удк 621.396.697
МОДЕЛЬ ДВИЖЕНИЯ КОСМИЧЕСКОГО ОБЪЕКТА И ФОРМИРОВАНИЕ ЕГО РАДИОЛОКАЦИОННОГО ПОРТРЕТА
А. Н. Детков, И. А. Макаров
ОАО «НПК НИИДАР», г.
Москва
Статья
получена 4 декабря 2013 г.
Аннотация: В рамках задачи радиолокационного наблюдения космического объекта (КО) с помощью РЛС, размещённой на поверхности Земли в точке с произвольной широтой, получены расчётные формулы, характеризующие кинематику его движения по круговой орбите с произвольным углом наклонения с учётом вращения Земли. Предложена модель учёта вращения Земли для корректной оценки полного времени наблюдения КО. Приведён показатель качества синтезирования, который даёт возможность выявления участков траектории КО, на которых производить его радиолокационное портретирование наиболее эффективно.
Ключевые слова: радиолокационная станция с инверсным синтезированием апертуры антенны (ИРСА), радиолокационный портрет цели, космический объект, разрешение по поперечной дальности.
Abstract: In the context of the problem of radar observations of space objects (SO) using the radar, located on arbitrary latitude on the Earth's surface, we obtained formulas describing the kinematics of motion in a circular orbit with an arbitrary inclination angle with the Earth's rotation. The model is proposed, accounting the rotation of the Earth, in order to estimate correctly the total observation time SO. An indicator of the quality of synthesis, which allows to identify portions of the trajectory SO, which make the most effective radar portraying, was proposed.
Keywords: ISAR, target radar image, space object, cross-range scaling.
Введение
для получения радиолокационных изображений (РЛИ) КО необходимо использовать когерентные РЛС, обладающие высоким разрешением как вдоль линии визирования (по дальности), так и в поперечном направлении (по азимуту). С помощью, соответствующих методов обработки радиолокационных сигналов можно оценить форму, размеры, параметры движения КО как радиолокационной цели, отражательные свойства его отдельных элементов, характеристики рассеяния КО [1 − 4].
Высокое разрешение по дальности обеспечивается использованием сложных (широкополосных) сигналов. Высокое азимутальное разрешение обеспечить весьма сложно, поскольку для получения узкой диаграммы направленности (ДН) необходимы очень большие (практически нереализуемые) антенны. Решить эту проблему можно с помощью антенн с синтезированной апертурой, которые реализуются при относительном движении КО и РЛС, имеющей реальную антенну с малым раскрывом [1, 2]. Синтез апертуры антенны в принципе возможен при любом виде движения объекта, источника облучающего сигнала и приёмного устройства. Важно лишь, чтобы при взаимном перемещении происходило изменение ракурса наблюдаемой цели. Синтезирование, основанное на использовании поступательного или вращательного движения объекта относительно неподвижной РЛС, получило название инверсного (Invеrsе Sуnthеtic Ареrture) [2].
Радиолокаторы с инверсным синтезированием апертуры (ИРСА) относятся к классу дальномерно-доплеровских систем. Принятый и демодулированный траекторный сигнал в такой РЛС обычно стробируется по дальности. В каждом канале дальности имеется набор полосовых фильтров, с помощью которых выполняется спектральный анализ сигнала. Система отображения, чувствительная к энергии сигнала на выходе каждого фильтра, формирует изображение объекта в координатах «доплеровская частота – дальность» [4].
Под траекторным сигналом (ТС) в ИРСА обычно понимают сигнал, принятый от КО в процессе его движения по орбите и достаточный по времени для получения радиолокационного изображения КО.
Траекторный сигнал является аналогом амплитудно-фазового распределения поля по раскрыву физической антенны (конформной антенной решетки произвольного профиля). Он определяет форму диаграммы направленности синтезированной антенны (импульсного отклика ИРСА) вдоль траектории полёта КО, получаемой в результате согласованной фильтрации сигнала [3].
В состав параметров ТС, знание которых необходимо для выбора технических параметров ИРСА, реализации алгоритмов синтеза радиолокационного изображения (РЛИ) и оценки разрешающей способности ИРСА вдоль линии пути КО (по азимуту), входят [5]:
временные зависимости
наклонной дальности до КО, а также фазы ![]() , однозначно определяемой наклонной
дальностью
, однозначно определяемой наклонной
дальностью ![]() при выбранной длине волны
при выбранной длине волны ![]() ИРСА:
ИРСА: ![]() .
.
временная зависимость
доплеровской частоты (производной фазы по времени): ![]() , с учётом которой выбирают частоту повторения зондирующих сигналов
ИРСА для исключения помех неоднозначности;
, с учётом которой выбирают частоту повторения зондирующих сигналов
ИРСА для исключения помех неоднозначности;
временная зависимость
амплитуды принятого сигнала от КО ![]() ;
;
длительность тpaeктopного
сигнала, определяющая максимальное время ![]() синтеза РЛИ или время обработки сигнала (кoгepeнтнoго накопления);
синтеза РЛИ или время обработки сигнала (кoгepeнтнoго накопления);
угловые размеры
синтезированной апертуры в пространстве ![]() ,
используемые при антенном подходе к анализу процессов синтеза РЛИ и оценке peaлизуемого
разрешения по азимуту (поперечной дальности);
,
используемые при антенном подходе к анализу процессов синтеза РЛИ и оценке peaлизуемого
разрешения по азимуту (поперечной дальности);
ширина спектра
доплеровских частот ![]() , ограниченная угловыми размерами
синтезированной апертуры в пространстве
, ограниченная угловыми размерами
синтезированной апертуры в пространстве ![]() и
определяющая выбор частоты повторения зондирующего сигнала;
и
определяющая выбор частоты повторения зондирующего сигнала;
разрешение ИРСА по
азимуту (поперечной дальности) − ![]() .
.
в перечисленном списке параметров
траекторного сигнала, часть из них (фаза, доплеровская частота) зависят не
только от рабочей длины волны ИРСА, но и прежде всего от параметров движения КО.
Предполагается, что временная зависимость фазы сигнала ![]() однозначно определена временной зависимостью наклонной дальности цели R(t)
через длину волны ИРСА. Однако при наблюдении ИРСА космических объектов с необходимо
учитывать ряд специфических факторов, к которым относятся [5]:
однозначно определена временной зависимостью наклонной дальности цели R(t)
через длину волны ИРСА. Однако при наблюдении ИРСА космических объектов с необходимо
учитывать ряд специфических факторов, к которым относятся [5]:
вращение Земли, вызывающее смещение доплеровского спектра и увеличенную миграцию дальности;
большая дальность наблюдения, предъявляющая высокие требования к энергетическому потенциалу ИРСА и точности фокусирования синтезированной апертуры;
высокая орбитальная скорость КО, которая приводит к существенной неопределенности зондирующего сигнала по азимуту или дальности;
деструктивные воздействия на трассе распространения сигнала (тропосферные и ионосферные нестабильности).
Создание и эксплуатация ИРСА разделяется на несколько стадий, в которых анализ воздействия перечисленных факторов имеет разные требования к точности знания параметров относительного движения. Высокая точность позиционирования КО при съемке требуется для «нацеливания» антенны радиолокатора на заданный участок траектории КО, вычисления опорной функции для синтеза РЛИ высокого разрешения и привязки РЛИ к соответствующим координатам с точностью до одного пикселя (отсчёта) РЛИ [5].
Преобразование первичной информации в координатах наклонная дальность − время излучения зондирующего импульса в координаты поперек и вдоль трассы движения КО требуют тщательного учёта доплеровского смещения принимаемого сигнала и параметров относительного движения. Для нацеливания радиолокатора на объект съемки необходимы измерение тeкущих координат КО, а также управление параметрами радиолокатора (частотой повторения, положением временных стробов приёма) и управление диаграммой антенны по углу места и азимуту. Необходимые управляющие параметры вводятся на основании баллистических расчетов движения КО, данных текущих траекторных измерений и параметров модели геоида.
Модель относительного движения космического объекта
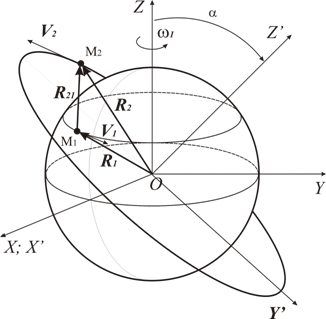
Для описания соотношений, определяющих положения КО и точки наблюдения, геометрию получаемого радиолокационного портрета, параметры принимаемого сигнала (фазу, доплеровскую частоту), используют различные системы координат: полярные (угловые) и прямоугольные (декартовы). К ним относятся (рис. 1) [6]:
1) геоцентрическая система координат (ГCK) OXYZ, в которой ось OZ направлена на север, ось OX в сторону нулевого меридиана, а ось OY дополняет ГСК до правой тройки;
2) введенная для удобства рассмотрения «опорная» система координат (ОCK) X’Y’Z’, образованная поворотом системы OXYZ вокpyг оси OZ таким образом, чтобы её ось OX’ была направлена в восходящий узел орбиты КО;
3) полярная географическая система
координат, характеризуемая широтой ![]() и долготой
и долготой ![]() (по Гринвичу), а также локальным радиусом
Земли Be или текущим paдиусом орбиты КО Rs.
(по Гринвичу), а также локальным радиусом
Земли Be или текущим paдиусом орбиты КО Rs.
Рис 1. Геометрия относительного движения точки наблюдения на Земле (М1) и космического объекта на круговой орбите (M2) в геоцентрической системе координат.
Для описания соотношений, определяющих относительное положение КО и точки наблюдения, рассмотрим следующие точки и векторы в ГCK:
М1 – точка наблюдения за космическим объектом, расположенная на Земле (место нахождения РЛС) и вращающаяся против часовой стрелки с периодом равным периоду вращения Земли;
М2 – точка (КО рассматривается как точечная цель), вращающаяся против часовой стрелки по круговой орбите вокруг Земли на некоторой высоте Н от поверхности Земли. На рис. 1 представлена модель Земли и относительного движения КО по круговой орбите и объекта на Земле (например, РЛС) в ГСК ОХYZ;
![]() – радиус вектор точки M1 (в ГCK ОХYZ);
– радиус вектор точки M1 (в ГCK ОХYZ);
![]() – радиус вектор точки M2 (в ГCK ОХYZ).
– радиус вектор точки M2 (в ГCK ОХYZ).
В ГCK ОХYZ соответствующие координаты
радиус-вектора ![]() могут быть записаны в виде:
могут быть записаны в виде:
где jÎ[-π/2;π/2] – широта точки М1 на Земле, F10 – начальная фаза, w1 – угловая частота вращения Земли.
В ОCK ОX’Y’Z’, которая получается из ГCK ОХYZ поворотом вокруг оси X на угол отклонения орбиты a, движение точки М2 по орбите производится в плоскости ОX’Y’ (см. рис.1). Для задачи определения параметров относительного движения точек М1 и M2, если нас интересуют не конкретные моменты времени, когда достигаются те или иные амплитудные значения, например, относительного расстояния между точками М1 и M2, радиальная составляющая их относительной скорости и др., а только сами эти значения допустимо среди всех орбит с заданным углом отклонения орбиты выбрать одну орбиту из соображений удобства, остальные возможные случаи могут быть получены заданием соответствующей разности начальных фаз движения точек М1 и М2 по своим траекториям.
В ОСК ОX’Y’Z’ координаты радиус-вектора ![]() могут быть записаны в виде:
могут быть записаны в виде:
где H – высота орбиты КО, F20 – начальная фаза движения КО, w2 – угловая частота вращения КО в гравитационном поле Земли [6]:
где G – гравитационная постоянная, М – масса Земли.
Известно [7], что поворот вокруг оси ОX на угол b в трёхмерном пространстве осуществляется с помощью матрицы поворота следующим образом:
В нашем случае, поскольку поворот осуществлён против направления положительного обхода, b = -a:
Окончательное выражение
для радиус-вектора ![]() в ГCK ОХYZ с учётом (2) имеет вид:
в ГCK ОХYZ с учётом (2) имеет вид:
Таким образом, радиус-вектор, определяющий изменение относительного положения точек М1 и М2 с течением времени равен:
![]()
а расстояние между ними зависит от времени следующим образом:
Ограничение времени наблюдения космических объектов
Очевидно, что точки М1
и М2 находятся не всегда в зоне прямой видимости наблюдателей,
поэтому накладываются ограничения на время наблюдения КО. Время нахождения КО в
зоне прямой видимости РЛС на широте j (с заданным углом наклонения a) может быть определено или численно с требуемой точностью
(например, при введении в цикле программы ограничения для функции![]() по дальности) или аналитически.
по дальности) или аналитически.
Рассмотрим некоторую точку D (не теряя общности рассуждений, для наглядности положим j=0) на Земле (Рис. 2). Проведём касательную плоскость к поверхности Земли в этой точке. Обозначим крайние точки А и С пересечения данной плоскости с круговой орбитой КО. Внутри короткой дуги АEС КО виден из точки D, вне её – исчезает из геометрического «поля зрения».
Рис. 2 Геометрия нахождения КО в зоне прямой видимости из точки наблюдения на Земле.
В точках А и С
радиус-вектора ![]() и
и ![]() ортогональны,
а полный угол «поля зрения» равен
ортогональны,
а полный угол «поля зрения» равен ![]() . Для нахождения
данного угла запишем условие ортогональности векторов
. Для нахождения
данного угла запишем условие ортогональности векторов ![]() и
и
![]() :
:
Векторное уравнение (9) с учётом (1) и (6) фактически представляет собой уравнение:
где ![]() ,
, ![]() .
.
Решая уравнение (10)
относительно угла ![]() получаем:
получаем:
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Из (11) следует, что искомый полный угол
«поля зрения» равен:
. Из (11) следует, что искомый полный угол
«поля зрения» равен:
![]()
Поскольку движение
космического объекта по окружности является равномерным, время углового
перемещения на угол ![]() (без учёта вращения Земли) есть
соответствующая доля от полного периода
(без учёта вращения Земли) есть
соответствующая доля от полного периода ![]() обращения
точки А на орбите высотой H:
обращения
точки А на орбите высотой H:
Учёт вращения Земли может
быть проведён следующим образом. Точка В имеет период обращения ![]() . Следовательно, если перейти в систему
отсчёта, связанную с Землей и вращающуюся вокруг оси Z с той же угловой скоростью
. Следовательно, если перейти в систему
отсчёта, связанную с Землей и вращающуюся вокруг оси Z с той же угловой скоростью ![]() это
будет эквивалентно тому, что Земля «неподвижна», но точка А, находясь на орбите
c высотой H, изменила период обращения:
это
будет эквивалентно тому, что Земля «неподвижна», но точка А, находясь на орбите
c высотой H, изменила период обращения:
 , (14)
, (14)
следовательно, интервал времени нахождения точки А в зоне прямой видимости из точки D в этом случае составит:
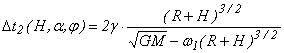 , (15)
, (15)
где 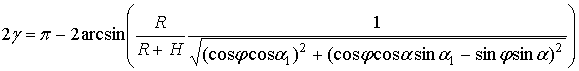
Полученные расчётные
зависимости ![]() представлены на рис. 3. Установлено, что
с увеличением высоты орбиты спутника время нахождения космического объекта в
зоне прямой видимости из точки на Земле увеличивается при фиксированном угле a и уменьшается с увеличением угла a.
представлены на рис. 3. Установлено, что
с увеличением высоты орбиты спутника время нахождения космического объекта в
зоне прямой видимости из точки на Земле увеличивается при фиксированном угле a и уменьшается с увеличением угла a.
|
|
|
|
а) |
б) |
|
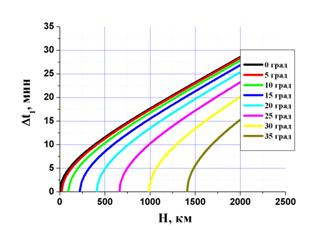
Рис. 3 Зависимости интервалов времени Dt1 и Dt2 нахождения космического объекта на орбите высотой H в зоне прямой геометрической видимости из заданной точки на Земле от высоты орбиты H при различных значениях угла наклонения a спутника (j=00; F10=F20=-900): а) без учёта вращения Земли; б) с учётом вращения Земли. |
|
Как и следовало ожидать,
учёт вращения Земли приводит к увеличению времени нахождения космического
объекта в зоне прямой геометрической видимости из заданной точки на Земле.
Зависимости абсолютной величины временной поправки ![]() от
высоты H орбиты спутника при различных значениях
угла наклонения a
орбиты КО, приведены на рис. 4.
от
высоты H орбиты спутника при различных значениях
угла наклонения a
орбиты КО, приведены на рис. 4.
|
|
|
|
а) |
б) |
|
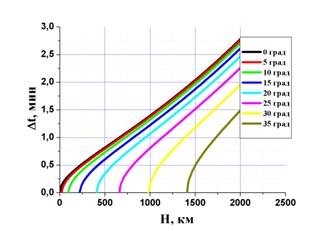
Рис. 4 Зависимость абсолютной (а) и относительной
(б) величины временной поправки |
|
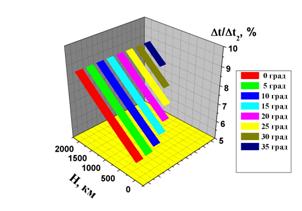
В целом абсолютное
значение величины ![]() растёт с увеличением высоты
орбиты спутника и тем меньше, чем больше модуль разности углов склонения
спутника и широты точки на Земле. Вместе с тем, относительная поправка
растёт с увеличением высоты
орбиты спутника и тем меньше, чем больше модуль разности углов склонения
спутника и широты точки на Земле. Вместе с тем, относительная поправка ![]() , как оказалось, не зависит от угла
склонения орбиты спутника, а только от высоты орбиты Н (см. рис.5).
, как оказалось, не зависит от угла
склонения орбиты спутника, а только от высоты орбиты Н (см. рис.5).
Вращение Земли можно учесть
и иным образом, если под углом 2γ в формуле
(13) понимать разность углов ![]() , где
, где ![]() – меньший орбитальный угол,
соответствующий появлению КО из-за горизонта относительно первичной точки
наблюдения на Земле, а
– меньший орбитальный угол,
соответствующий появлению КО из-за горизонта относительно первичной точки
наблюдения на Земле, а ![]() – больший орбитальный угол, соответствующий
уходу КО за горизонт относительно новой точки наблюдения на Земле в момент
времени спустя
– больший орбитальный угол, соответствующий
уходу КО за горизонт относительно новой точки наблюдения на Земле в момент
времени спустя ![]() . Как показывает численное моделирование, временная поправка
на вращение Земли, полученная таким способом не превышает нескольких секунд на
временах наблюдения до получаса.
. Как показывает численное моделирование, временная поправка
на вращение Земли, полученная таким способом не превышает нескольких секунд на
временах наблюдения до получаса.
Траекторные параметры наблюдения КО
Один из главных
траекторных параметров, определяющих энергетику применяемой для наблюдения КО
РЛС, является относительная дальность ![]() . На
практике бывает важно знать зависимость дальности до КО не от времени, а от
угла между зенитной точкой траектории цели и текущим направлением на цель -
углом b
(рис. 2). Однако, в том случае, если КО находится на орбите с произвольным
углом наклонения и наблюдается из точки на Земле на произвольной широте, удобно
ввести угол наблюдения b’ между радиус-векторами
. На
практике бывает важно знать зависимость дальности до КО не от времени, а от
угла между зенитной точкой траектории цели и текущим направлением на цель -
углом b
(рис. 2). Однако, в том случае, если КО находится на орбите с произвольным
углом наклонения и наблюдается из точки на Земле на произвольной широте, удобно
ввести угол наблюдения b’ между радиус-векторами ![]() и
и![]() , полученными в момент
, полученными в момент ![]() обнаружения КО и в текущий момент времени
t соответственно:
обнаружения КО и в текущий момент времени
t соответственно:
где
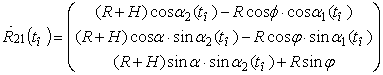 ,
,
![]() ,
, 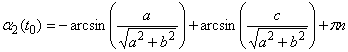 ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
|
|
|
|
а) |
б) |
|
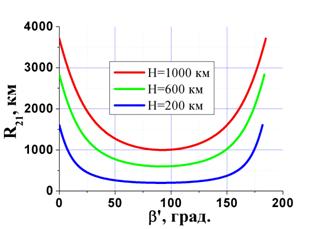
Рис. 6 Зависимости расстояния R21 между точкой на орбите и точкой на Земле от угла b’ для различных высот орбит H и различных значениях угла наклонения a КО (j=00; F10=F20=-900): а) a=00, б) a=100. |
|
На рис. 6 представлены соответствующие зависимости расстояний между точкой М2 на орбите с различными высотами H и точкой М1 на Земле от угла b’ при различных углах наклонения орбиты КО, рассчитанные с использованием формул (7), (8) и (19) в диапазоне интервалов времён наблюдения КО.
Ещё одним важным
траекторным параметром является относительная скорость ![]() наблюдения
КО, которая может быть рассчитана как производная по времени от радиус-вектора
относительного положения точек М1 и М2 с использованием
формул (7), (8):
наблюдения
КО, которая может быть рассчитана как производная по времени от радиус-вектора
относительного положения точек М1 и М2 с использованием
формул (7), (8):
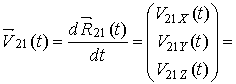
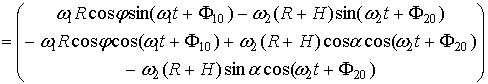 . (17)
. (17)
Для нахождения
доплеровских сдвигов частоты зондирующего радиоизлучения в условиях различной
геометрии наблюдения КО с точки наблюдения, находящейся на Земле, необходимо
вычислить радиальную составляющую относительной скорости Vr(t) на направление, задаваемое радиус-вектором ![]() :
:
С учётом определения
векторов ![]() и
и ![]() значение
относительной скорости
значение
относительной скорости ![]() будет принимать отрицательные значения при сближении
точек М1 и М2 и положительные – при их «разбегании». На
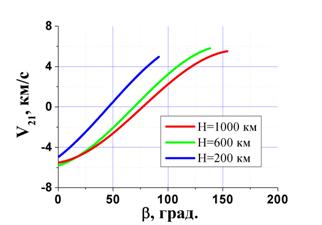
рис. 7 представлены зависимости радиальной составляющей скорости Vr между точкой на орбитах с различной
высотой H и точкой на Земле от угла b’ для различных высот орбит H и различных разностях угла склонения орбиты и широты точки
на Земле в диапазоне расчётных интервалов времён наблюдения КО.
будет принимать отрицательные значения при сближении
точек М1 и М2 и положительные – при их «разбегании». На
рис. 7 представлены зависимости радиальной составляющей скорости Vr между точкой на орбитах с различной
высотой H и точкой на Земле от угла b’ для различных высот орбит H и различных разностях угла склонения орбиты и широты точки
на Земле в диапазоне расчётных интервалов времён наблюдения КО.
|
|
|
|
а) |
б) |
|
Рис. 7 Зависимости относительной скорости Vr между точкой на орбитах с различной высотой H и точкой на Земле от угла b для различных высот орбит H и различных значениях угла a наклонения орбиты КО (j=00; F10 = F20= - 900): а) a=00, б) a=100. |
|
Доплеровская частота траекторного сигнала КО
При наблюдении КО с помощью РЛС, расположенной на поверхности Земли, величины формирующихся доплеровских сдвигов частоты зондирующего радиоизлучения определяются как [1]:
В общем случае
доплеровская частота ![]() зависит от многих факторов: времени,
азимутального угла наблюдения КО, угла склонения и высоты орбиты, широты точки
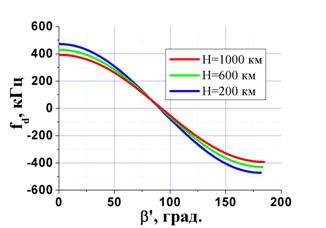
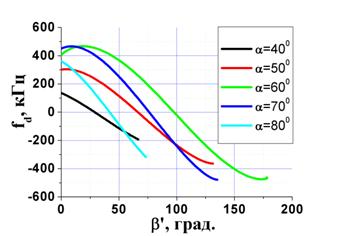
наблюдения на Земле. Эти зависимости иллюстрируются кривыми на рис. 8-9.
зависит от многих факторов: времени,
азимутального угла наблюдения КО, угла склонения и высоты орбиты, широты точки
наблюдения на Земле. Эти зависимости иллюстрируются кривыми на рис. 8-9.
|
|
|
|
а) |
б) |
|
Рис. 8 Зависимости доплеровской частоты |
|
|
|
|
|
а) |
б) |
|
Рис. 9 Зависимости доплеровской частоты |
|
Приращение требуемого
углового сектора Dβ −
углового размера синтезированной апертуры антенны в режиме ИРСА зависит от
значения требуемой разрешающей способности по азимуту (поперечной дальности) ![]() . В свою очередь, РС по азимуту зависит от
девиации доплеровской частоты:
. В свою очередь, РС по азимуту зависит от
девиации доплеровской частоты:
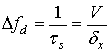 ,
(20)
,
(20)
где ![]() −
интервал синтезирования, V
− линейная скорость КО.
−
интервал синтезирования, V
− линейная скорость КО.
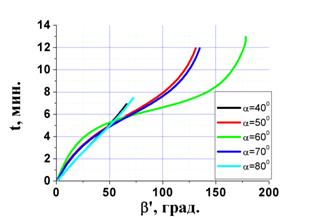
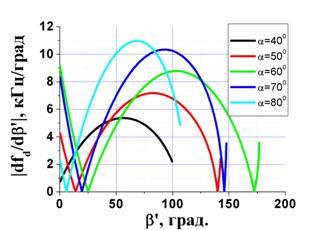
Таким образом, для оценки
времени синтезирования для конкретных углов наблюдения КО с заданной широты и
при заданном наклонении орбиты КО необходимо ещё иметь зависимости ![]() (рис. 10). Рис. 9 и 10 при взаимном сопоставлении
позволяют оценить интервал синтезирования, необходимый для набега доплеровской
частоты, отвечающего заданному азимутальному разрешению.
(рис. 10). Рис. 9 и 10 при взаимном сопоставлении
позволяют оценить интервал синтезирования, необходимый для набега доплеровской
частоты, отвечающего заданному азимутальному разрешению.
|
|
|
|
а) |
б) |
|
Рис. 10 Зависимости времени t наблюдения КО от угла b’ для орбит с различной высотой H и при различных значениях угла a склонения орбиты спутника (j=600; F10=F20=00): а) Н=600 км, б) Н=1000 км. |
|
Из рис. 10 видно, что
условия инверсного синтезирования под различными углами ![]() различны.
Для оценки возможности выполнения требований по РС при заданных значениях
траекторных параметров движения КО можно ввести следующий показатель качества
синтезирования
различны.
Для оценки возможности выполнения требований по РС при заданных значениях
траекторных параметров движения КО можно ввести следующий показатель качества
синтезирования
 ,
(21)
,
(21)
который не зависит от знака ![]() .
.
Для удобства
использования (21) на практике устремим приращения конечных разностей к нулю. В
этом случае по определению показатель качества синтезирования является
производной доплеровской частоты ![]() по углу
по углу ![]() :
:
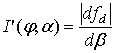 .
(22)
.
(22)
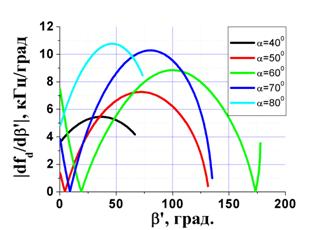
Пример расчёта показатель качества синтезирования для различных условий применения показан на рис. 11.
|
|
|
|
а) |
б) |
|
Рис. 11 Зависимости модуля скорости изменения
доплеровской частоты |
|
Из
графиков рис. 10 видно, что имеются участки траектории, где ![]() и на которых портретирование КО можно
проводить с минимальным угловым раскрывом синтезированной апертуры (следовательно
– минимальным временем синтезирования) при заданной разрешающей способности.
и на которых портретирование КО можно
проводить с минимальным угловым раскрывом синтезированной апертуры (следовательно
– минимальным временем синтезирования) при заданной разрешающей способности.
Выводы
В ИРСА при получении траекторного сигнала от КО, движущегося по баллистической траектории, требуется учёт скорости вращения Земли. Предложена модель учёта вращения Земли для корректной оценки времени наблюдения КО, построения зависимостей дальностей от РЛС до КО от времени наблюдения и от угла визирования, а также для расчёта аналогичных зависимостей радиальной скорости КО и доплеровской частоты.
Предложена модель движения КО, позволяющая оценивать основные параметры траекторного сигнала от КО при размещении РЛС на поверхности Земли в точке с произвольной широтой. Установлены условия оптимального портретирования КО при его движении по круговой орбите с произвольным углом наклонения.
1. Радиолокационные станции с цифровым синтезированием апертуры антенны// Под ред. В.Т. Горяинова. – М.: Радио и связь, 1988.
2. Зиновьев Ю.С., Пасмуров А.Я. Методы обращённого синтезирования апертур в радиолокации с помощью узкополосных сигналов // Зарубежная радиоэлектроника, 1985, № 3. – С. 27 – 39.
3. Пасмуров А.Я. Получение радиолокационных изображений летательных аппаратов // Зарубежная радиоэлектроника, 1987, № 12. – С. 3 – 30.
4. Fu X., Wu J., Zhao H., Chen D., Gao M. Inverse synthetic aperture radar imaging and crossrange scaling for space objects. – IEEE 5th International Congress on Image and Signal Processing (CISP 2012), 2012, Р. 1827-1831.
5. Радиолокационные системы землеобзора космическоrо базирования / Под ред. Л.Б. Неронского. – М.: Радиотехника, 2010.
6. Единая государственная общеземная геоцентрическая система координат «Параметры Земли 1990 года» (ПЗ-90.11): Постановление Правительства Российской Федерации от 28 декабря 2012 г. № 1463 «Об установлении общеземной геоцентрической системы координат в качестве государственной системы координат для использования в целях геодезического обеспечения орбитальных полётов и решения навигационных задач».
7. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Наука, 1984.