“ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ” N 12, 2013

оглавление

КОМБИНИРОВАННАЯ ДВУХКРИТЕРИАЛЬНАЯ ОПТИМИЗАЦИЯ ЛИНЕЙНЫХ ПРЕКОДЕРОВ СИСТЕМЫ MIMO С АЛГЕБРАИЧЕСКОЙ РОТАЦИЕЙ СИМВОЛЬНОГО СОЗВЕЗДИЯ

 

В. П. Волчков, А. А. Шурахов

Московский технический университет связи и информатики (МТУСИ)

Статья получена 12 декабря 2013 г.

 

Аннотация. Приведен синтез комбинированных двухкритериальных алгоритмов линейного прекодирования для систем MIMO. В качестве первого критерия использован максимум пропускной способности системы, а в качестве второго – максимизация минимального расстояния между точками созвездия на выходе канала MIMO. Представлены результаты моделирования предложенных алгоритмов. Показано, что для конфигураций MIMO-8x8 и MIMO-4x4 комбинированные двухкритериальные прекодеры c ротацией созвездия позволяют получить выигрыши в помехоустойчивости порядка 17 дБ и 14 дБ, соответственно, по сравнению с известными однокритериальными прекодерами. Основные результаты данной статьи докладывались на 6-ой Всероссийской научно-технической конференции «Радиолокация и радиосвязь»

Ключевые слова: MIMO система, линейный прекодер, ротация символьного созвездия, помехоустойчивость, пропускная способность.

Abstract. The synthesis of combined two-criteria algorithms for MIMO linear precoders is presented. The first criterion of these algorithms is a maximization of capacity of MIMO system, the second criterion – maximization of distance between points of signal constellation at output of MIMO channel. The results of algorithms simulation are provided. For MIMO-8x8 and MIMO-4x4 configurations combined two-criteria algorithms have correspondingly 17 dB and 14 db gain in BER versus well-known one-criterion algorithms.

Keywords: MIMO system, linear precoder, rotation of symbol constellation, interference robustness, capacity.

 

1.                Описание проблемы

Линейное прекодирование в системах MIMO позволяет гибко управлять пропускной способностью и помехоустойчивостью при достаточно простых технических реализациях [1]. Исследования [2] показали, что системы линейного прекодирования, построенные на одном критерии оптимальности и использующие линейный приемник, диагонализируют сквозную матрицу приемно-передающего тракта и тем самым значительно упрощают алгоритмы декодирования. Однокритериальные линейные прекодеры получить выигрыш в помехоустойчивости по сравнению с MIMO системой без прекодирования, когда максимальное количество виртуальных информационных потоков прекодера  меньше числа передающих антенн , т.е. . Если , однокритериальные прекодеры обладают неудовлетворительными характеристиками BER.

В работе [3] показано, что значительно улучшить характеристики системы MIMO, использующей линейное прекодирование, можно с помощью двухкритериальных прекодеров, построенных на совместном использовании критериев максимизации пропускной способности и помехоустойчивости системы. Платой за это является необходимость применения многомерного ML демодулятора.

В настоящей работе рассматривается дальнейшее усовершенствование двухкритериальных прекодеров за счет применения более общего критерия оценки помехоустойчивости и усложнения структуры матрицы линейного прекодирования [4].
 

2.  Формулировка задачи и ее решение

Классическая модель MIMO канала с линейным прекодером описывается уравнением (см. рис. 1).

,                                        (1)

где – вектор комплексных информационных символов из многомерного сигнального созвездия;  – вектор передаваемых комплексных символов;  – комплексная матрица прекодера;  – вектор принимаемых информационных символов;  – комплексный гауссовский вектор шумов с нулевым средним и ковариационной матрицей  («*» – символ эрмитового сопряжения);  – комплексная матрица MIMO канала, элементы которой случайны, но идеально оцениваются и известны на приемной и передающей сторонах. Последнее обеспечивается за счет цепи обратной связи, по которой оценка канала передается на передатчик. Передаваемая через все антенны мощность постоянна и равна .
 

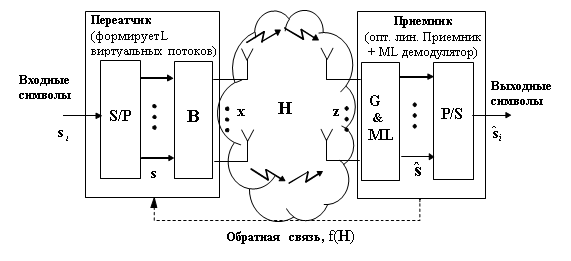
Рис 1. Система MIMO с линейным прекодером.

 

В [2] показано, что однокритериальные оптимальные прекодеры, построенные по критерию минимизации СКО на выходе декодера, либо максимизации отношения C/Ш или максимизации пропускной способности канала, имеют структуру вида:

                                                 (2)

где матрица  для всех прекодеров одинакова и состоит из L собственных векторов матрицы H*H, упорядоченных по возрастанию собственных чисел, а диагональная матрица  – зависит от используемого критерия оптимальности

Для двухкритериальных прекодеров, рассмотренных в работе [3], матрица прекодирования строится на основе двух разных критериев оптимальности и имеет следующий вид:

,                                               (3)

где ,  – оптимальные матрицы прекодера по следующим критериям:

 :  ,          (4)

 :  ,                                (5)

Здесь  – целевые функции критериев;  – множество комплексных матриц размерности ;  – множество квадратных унитарных матриц размерности ; . Критерий (4) максимизирует пропускную способность MIMO канала (1), а критерий (5) нацелен по повышение помехоустойчивости и максимизирует монотонно возрастающую функцию  от условной оценки  нижней границы среднего квадрата расстояния  между любыми двумя точками ,  преобразованного созвездия  на выходе MIMO канала (1), т.е..

В качестве условия  в [3] рассматривались два варианта:

i) , т.е. известна матрица канала, а точки созвездия  случайны с параметрами ; ;

ii) , т.е. фиксированы произвольные точки созвездия , а матрица канала  – случайна.

В данной работе рассматривается более общий комбинированный вариант 2-го критерия, одновременно учитывающий случайность точек созвездия  и матрицы . Для этого представим матрицу  в виде произведения двух унитарных матриц – диагональной  и недиагональной матрица . Обозначим ,  и вместо (5) определим комбинированный критерий оптимальности:

                                                               (6)

,                                            (7)

                                                   (8)

Здесь  – оценка нижней границы среднего квадрата расстояния , при условии, что матрица канала известна;  – оценка нижней границы среднего квадрата расстояния , где ,  – любые две точки преобразованного созвездия .

Таким образом, в новой постановке линейный оптимальный прекодер имеет факторизованную матричную структуру

,                                                        (9)

где матрицы , ,  удовлетворяют критериям (4), (7), (8).

1. Решение экстремальной задачи (4) методом множителей Лагранжа [3] приводит к результату:

                                           (10)

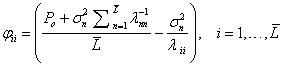,       (11)
 

где матрица  состоит из  первых столбцов ортогональной матрицы  , участвующей в SVD разложении . Элементы ,  диагональных матриц ,  положительны и упорядочены по убыванию, а значение  определяется так, что  для и  для .

2. Для решения оптимальных задач (6-8) обозначим , , . Матрица  является эрмитовой:

.

C учетом свойств следа матрицы  получаем:

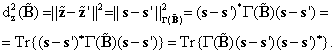
Условная оценка нижней границы определяется правой частью неравенства:
 


 

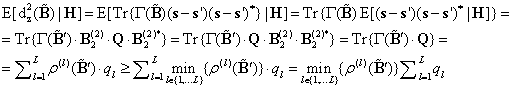
где  – диагональные элементы матрицы:

                                  (12)

Тогда, экстремальная задача (7) принимает вид

                                        (13)

и сводится к максимизации минимального элемента, стоящего на диагонали матрицы .

Учитывая (10), нетрудно убедиться, что матрица  является диагональной размерности  с вещественными неотрицательными элементами.

          
 

Следовательно, согласно (12),(13) оптимальное решение  должно обладать следующими свойствами – это недиагональная унитарная матрица, которая преобразованием унитарного подобия  переводит любую диагональную матрицу  в эрмитовую матрицу  с максимально возможным минимальным элементом на главной диагонали.

Учитывая, что преобразование  сохраняет след матрицы, т.е.

               ,                                     (14)
 

покажем, что в задаче (13) минимальный элемент  будет иметь максимальное значение, в случае, когда:

    ,                                                  (15)

Действительно, пусть существует преобразование , при котором, . В этом случае , что противоречит условию (14).

Условие (15) означает, что оптимальная унитарная матрица  в экстремальной задаче (13) должна с помощью преобразования  приводить к эрмитовой матрице  с одинаковыми элементами на главной диагонали.

Известно [5,6], что класс таких оптимальных решений достаточно широк. В частности, этому требованию удовлетворяют следующие унитарные матрицы:

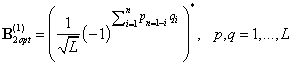   (матрица Walsh, Proposal 1)    (16)

     (матрица DFT, Proposal 2)    (17)

где ,  – i-ыe разряды двоичного представления чисел и , соответственно.

3. Рассмотрим теперь синтез оптимальной матрицы . В этом случае матрица канала  случайна, а  – диагональная матрица с некоррелированными случайными элементами , которые сложным образом зависят от элементов случайной матрицы канала . Но можно аппроксимировать их вероятностные характеристики - распределением с  степенями свободы [7]. Тогда , и обозначая

,                                        (18)

можно записать неравенство:

,

где под знаком произведения стоят только ненулевые компоненты вектора , число которых равно . При этом было учтено, что среднее геометрическое всегда не больше среднего арифметического. Поскольку последнее неравенство справедливо для любых точек созвездия, то

                           

В результате критерий (8) принимает вид

,                                      (19)

где выражение, стоящее в круглых скобках, характеризует, так называемое, алгебраическое разнесение точек повернутого созвездия .

Экстремальная задача (19) сводится к нахождению наилучшей диагональной алгебраической ротации в преобразовании (15) точек созвездия. Ее решение известно [8] и имеет следующий вид

,                        (20)

где угол поворота  зависит от размерности матрицы L. В частности, для наиболее типичных случаев этот параметр принимает следующие значения:

                   

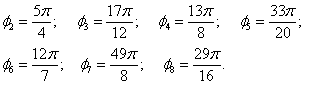
Таким образом, оптимальный линейный прекодер , синтезированный по комбинированному критериям (4), (7), (8), определяется в двух вариантах. 1) Прекодер «Walsh+DiagRot»: вычисляется по формулам (10)-(11) а  и  – по формулам (16) и (20). 2) Прекодер «Fourier+DiagRot»:  вычисляется по формулам (10)-(11), а  и  – по формулам (17) и (20).

 

3.  Моделирование и выводы

Анализ эффективности синтезированных прекодеров проводился на основе характеристик BER, построенных как функции от SNR. Сравнение прекодеров проводилось на уровне BER равном 0,001. Результаты моделирования характеристик BER для комбинированных двухкритериальных прекодеров в конфигурациях MIMO 8х8 и 4х4 представлены на рисунках 2-4. На этих рисунках для сравнения так же приведены характеристики BER двух однокритериальных линейных прекодеров, рассмотренных в [2], один из которых максимизирует пропускную способность MIMO канала (на графиках обозначен “Max-Capacity”), а другой прекодер минимизирует среднеквадратическую ошибку на выходе линейного декодера (обозначен на графиках “Min-Trace (MSE)”).

 

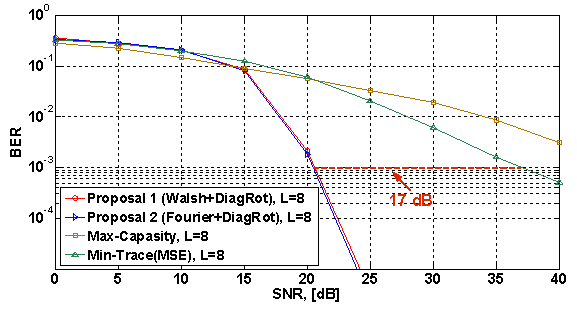
Рис 2. Характеристики BER (система QAM-4, 8x8, L=8, некоррелированный канал)

 

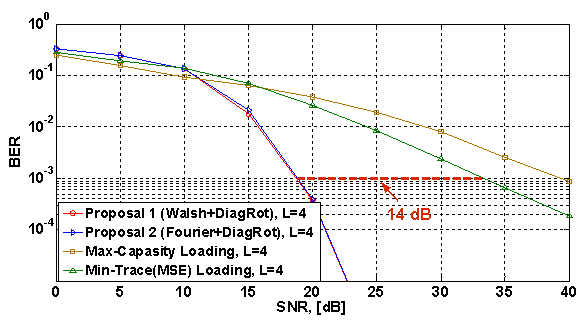
Рис 3. Характеристики BER (система QAM-4, 4x4, L=4, некоррелированный канал)

 

Результаты моделирования показывают, что комбинированные прекодеры «Walsh+DiagRot» и «Fourier+DiagRot» обладают примерно одинаковыми характеристиками BER. Причем, в конфигурациях MIMO-8x8 и MIMO-4x4 при некоррелированном MIMO канале комбинированные двухкритериальные прекодеры дают выигрыш в помехоустойчивости по сравнению с известными однокритериальными прекодерами порядка 17 дБ и 14 дБ соответственно (см. рисунки 2-3).

В коррелированном MIMO канале (моделирование проводилось по модели, описанной в отчете 3GPP TR 25.996 для сценариев “urban micto” и “urban macro”) комбинированные двухкритериальные критерии в конфигурации MIMO-8x8, L=8 достигают значений BER=10-3 при SNR порядка 40 дБ (см. рис. 4), что значительно ниже (на 21 дБ и 17 дБ, соответственно – см. рис 2 и рис. 3) характеристик, которые данные критерии имеют в некоррелированном канале, но сравнимы с показателями BER, которые достигают однокритериальные прекодеры в некоррелированном канале (см. рис. 2).

Для анализа комбинированных прекодеров так же получена оценка пропускной способности MIMO канала. Для оценки пропускной способности  MIMO канала проводился расчет дополняющей кумулятивной функции распределения Pc :

,

где  – пропускная способность MIMO канала при заданной реализации матрицы H. Вычисление функции CCDF производилось методом Монте-Карло путем подсчета частоты появления события  в серии независимых экспериментов при заданных значениях SNR.

На рисунке 5 показана дополняющая кумулятивная функция распределения пропускной способности MIMO 8x8 некоррелированного канала для случая SNR=15 дБ. Из рисунка видно, что синтезированные прекодеры имеют максимальную пропускную способность, как и однокритериальный прекодер “Max-Capacity”, что согласуется с принятыми при выводе комбинированных прекодеров критериями.

 


Рис 4. Характеристики BER (система QAM-4, 8x8, L=8, коррелированный канал)

 
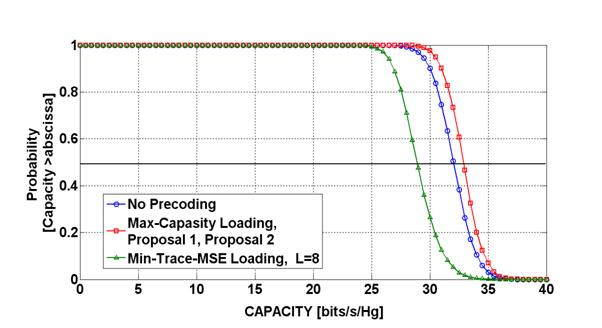
Рис 5. Оценка пропускной способности MIMO канала (SNR=15 дБ, 8x8, L=8, некоррелированный канал)

Литература

1.     A. Scaglione, P. Stoica, S. Barbarossa, G. B. Giannakis, and H. Sampath, "Optimal designs for space-time linear precoders and decoders,"IEEE Trans. Signal Process., vol. 50, no. 5, pp. 1051-1064, May 2002.

2.     Волчков В.П., Шурахов А.А. Исследование эффективности алгоритмов линейного прекодирования в системах MIMO.// Электросвязь. – 2012. – № 5. – С. 15-16.

3.     Волчков В.П., Шурахов А.А. Синтез двухкритериальных линейных прекодеров для системы MIMO.// Электросвязь. – 2013. – № 5. – С. 13-17.

4.     Волчков В.П., Шурахов А.А. Комбинированная двухкритериальная оптимизация линейных прекодеров системы MIMO с алгебраической ротацией символьного созвездия. VI Всероссийская конференция «Радиолокация и радиосвязь», (19-22 ноября) Москва, 2012 г. Сб. докладов, Том.2, с. 141-145.

5.     Р. Хорн, Ч. Джонсон. Матричный анализ. М.: Мир, 1989.

6.     В.В.Воеводин, Е.Е.Тыртышников. Вычислительные процессы с теплицевыми матрицами. – М. Наука. 1987

7.     Space-time wireless systems. From array processing to MIMO communications. Edited by H. Bolcskei, D. Gesbert, C.B. Papadias, A.J. Van Der Veen. Cambridge University Press. 2006.

8.     Zhiqiang Liu and E. Georgios B. Giannakis, “Linears Constellation Precoding for OFDM With Maximum Multipath Deversity and Coding Gains”, IEEE Transactions on Communications, vol. 51, n. 3, pp. 416-427, March 2003.