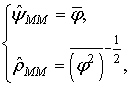СРАВНЕНИЕ МАКСИМАЛЬНО ПРАВДОПОДОБНОЙ И МОМЕНТНОЙ ОЦЕНОК ИНТЕГРАЛЬНОЙ РАЗНОСТИ ФАЗ

 

 А. С. Гвоздарёв, Т. К. Артёмова, К. С. Артёмов

Ярославский государственный университет им. П.Г. Демидова

Статья получена 4 декабря 2013 г.

 

Аннотация. В работе рассмотрен процесс построения оценки максимального правдоподобия и оценки методом моментов интегральной разности фаз применительно к эталонному минимально-фазовому методу. Проанализированы поведение смещения оценок и их рассеяние для случая различных истинных значений интегральной разности фаз, отношения сигнал/шум и объёма статистической выборки. Проведено качественное сравнение поведения оценок для различных практических ситуаций. Полученные характеристики могут использоваться для определения необходимого объёма выборки при фиксированной эталонной сетке или для формирования эталонной сетки при заданном объёме выборки для обеспечения требуемых характеристик оценки. На их основе можно выдать рекомендации к процессу проектирования систем, использующих минимально-фазовый метод.

Ключевые слова: оценка параметров, система голографического радиовидения, эталонный метод, интегральная разность фаз.

Abstract. Integral phase maximum likelihood and method of moments estimation procedures are analyzed in application to minimum-phase method. Their bias’ and variances’ dependence on signal-to-noise ratio, noiseless integral phase and sample size are analyzed. A qualitative study of behavior of estimates for different practical scenarios is performed. The obtained characteristics can be used to specify the required sample size for assuring fixed test-set step and for test-set construction in case of prespecified sample size. Guidelines for design process of the holographic system exploiting minimum-phase method are proposed.

Key words: parameter estimation, radioholographic system, reference set method, integral phase difference.

Введение

В работах [1-7] была показана возможность повышения качества оценки параметров радиоголографических объектов за счёт применения эталонных методов [1-3] и в частности минимально-фазового метода (МФМ) [4-7]. В МФМ оценка  исследуемого объектного параметра  формируется на основе оценки  интегральной разности фаз (ИРФ)  – модуля аргумента скалярного произведения объектного поля (радиоголограммы)   и набора  заранее сформированных эталонов . При этом характеристики  зависят от выбранной процедуры её проведения. Для получения оценки ИРФ по данным серии из измерений могут использоваться любые методы классической теории оценивания.

Одним из наиболее широко используемых подходов является максимально правдоподобное оценивание (МП) [8-9]. Однако, учитывая сложность процедуры получения и самих выражений для вероятностных характеристик , использование метода максимального правдоподобия приводит к вычислительно затратным процедурам. На практике  удобнее выбирать наиболее простые процедуры, обеспечивающие необходимое качество окончательной оценки. К ним, в частности, относится оценка методом моментов (ММ) [10]. Однако, в виду сложности реализующихся на практике моделей распределения шума, аналитически найти характеристики оценки (смещение и дисперсию/рассеяние) в широком диапазоне изменения параметров (объёма выборки, отношения сигнал/шум (ОСШ), времени наблюдения, параметров распределения и др.) удаётся крайне редко.

В связи с этим особую актуальность приобретает задача определения статистических характеристик искомых оценок  и  путём математического моделирования, и их сравнения с целью выбора процедуры оценивания, более удобной для широкого круга  возникающих на практике ситуаций.

 

Модель минимально-фазового метода

Для построения МП и ММ оценки ИРФ и анализа их поведения воспользуемся моделью МФМ, описанной в [7]. Будем предполагать, что  регистрируется в присутствии комплексного аддитивного белого гауссового шума  с нулевым матожиданием и дисперсией  по синфазной и квадратурной компонентам поля.

В [3] получено выражение для ИРФ, которое можно переписать в форме:

,                       (1)

где   ,  – истинное значение интегральной разности фаз в отсутствие шумов,  – конфлюэнтная гипергеометрическая функция, , а  – коэффициент, равный произведению отношения сигнал/шум  и коэффициента амплитудного расхождения , определяющего несоответствие амплитудных радиоголограмм исследуемого объекта и эталона, выбранного для сравнения.

Можно отметить, что (1) не удовлетворяет критерию факторизации, т.е. достаточной статистики найти не удаётся, а значит, в соответствии с критерием факторизации Неймана-Фишера [11] оптимальной оценки тоже найти не удастся. Исходя из этого, можно заключить, что получаемая ММ оценка будет в лучшем случае лишь асимптотически оптимальной.

 

Оценка максимального правдоподобия

Учитывая, что логарифм функции правдоподобия (ФП) для выборки  из отсчётов определяется выражением:

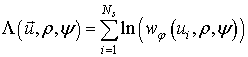,                                                            (2)

МП оценка  истинного значения интегральной разности фаз  будет искаться путём максимизации полученного логарифма ФП:

,                                                           (3)

 

Стоит отметить, что полученная плотность вероятности не относится к экспоненциальному семейству и не удовлетворяет критерию факторизации, а, следовательно, процедура максимизации функционала (2) при большом объёме выборки будет являться достаточно трудоёмкой. Исходя из этого, удобнее воспользоваться алгоритмом прямого поиска корня уравнения

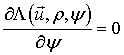,                                                                    (4)

которое может быть записано в следующей форме:

,                                                   (5)

где .

 

Оценка методом моментов

Для нахождения оценки  методом моментов воспользуемся полученными в [6] выражениями для математического ожидания и дисперсии ИРФ . Разлагая их в ряд Тейлора по параметру  и ограничиваясь точностью порядка , т.е., используя второе приближение) получим:

                                                                      (6)

Тогда в соответствии с методом моментов оценки для  и  (обозначим их  и ) могут быть найдены достаточно простым образом:

                                                            (7)

где черта над величиной означает взятие её выборочного среднего.

При совпадении объекта с одним из эталонов  и из (1) , т.е. выражение (6) примет вид: .

 

Статистический анализ максимально правдоподобной и моментной оценок

При проведении статистического анализа характеристик оценок в зависимости от отношения сигнал/шум и истинного значения интегральной разности фаз были выбраны значения параметров моделирования такие же, как и в работе [6]: =10³ и 2·10³, , ,  от 5  до 20 дБ (для метода максимального правдоподобия) и от 1  до 20 дБ (для метода моментов).

Для нахождения  и  в соответствии с (5) и (7) в среде Wolfram Mathematica для каждого значения ОСШ  от 1 до 20 дБ с шагом 1 дБ и для ряда значений истинной интегральной разности фаз  от 1 до 30 градусов была сгенерирована выборка 10⁶ отсчётов из распределения (1). Отсчёты были сгруппированы в 10³ групп по 10³ отсчётов в каждой. Для каждой группы было проведено оценивание, в результате чего для каждой пары значений ОСШ и  было получено 10³ оценок. Для каждого набора оценок была построена гистограмма и проверена гипотеза о нормальности их распределения по критерию Колмогорова-Смирнова с уровнем значимости 0,05. Для полученного набора оценок были рассчитаны смещения и рассеяния оценок.

Результаты моделирования показали, что получаемая МП оценка ИРФ существенно зависит от объема статистической выборки, доступной для анализа. Из рисунков 1 и 2  (где для наглядности при   приведено десятикратное значение рассеяния) видно, что при тех же исходных данных, что и в [6], оценка при малых ИРФ (до 1°) получается смещённой даже при больших ОСШ. С увеличением ИРФ смещение оценки при ОСШ более 12 дБ становится незначительным (выполняется свойство асимптотической несмещённости МП оценок [7]). Рассеяние оценки также демонстрирует немонотонное поведение при ОСШ до 14 дБ и ИРФ до 10°, что затрудняет возможность использования таких оценок.

 

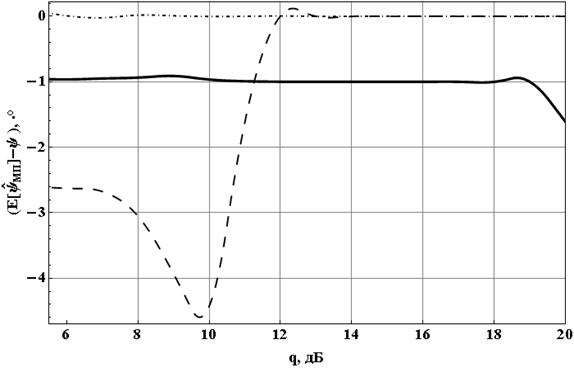
Рис. 1 Смещение оценки для случаев  (сплошная кривая),  (пунктирная кривая),  (штрихпунктирная кривая) при объёме  выборки 1000 отсчётов

 

 

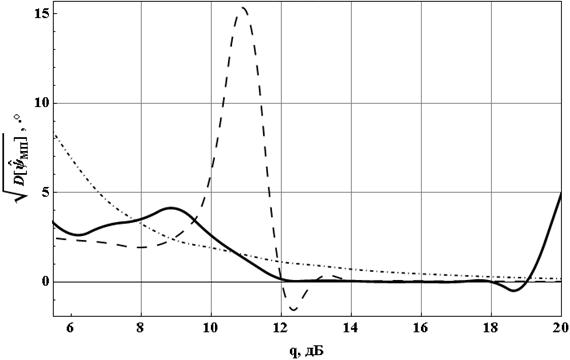
Рис. 2 Корень из рассеяния оценки для случаев  (сплошная кривая),  (пунктирная кривая),  (штрихпунктирная кривая)

 при объёме  выборки 1000 отсчётов

 

Для улучшения характеристик МП оценок объём статистической выборки был увеличен в 2 раза. Полученные результаты, представленные на рисунках 3 и 4, продемонстрировали недостаточность объёма выборки в 1000 отсчётов. При увеличении объёма выборки существенно улучшается поведение рассеяния и смещения оценки в области малых ОСШ. Для удобства сравнения на рисунке 3 график для случая =2·10³ приведён с десятикратным увеличением.

 

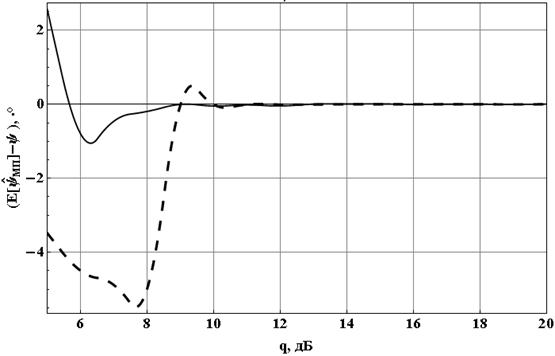
Рис. 3 Смещение оценки  для при объёме  выборки 1000 отсчётов (сплошная кривая) и 2000 отсчётов (пунктирная кривая)

 

 

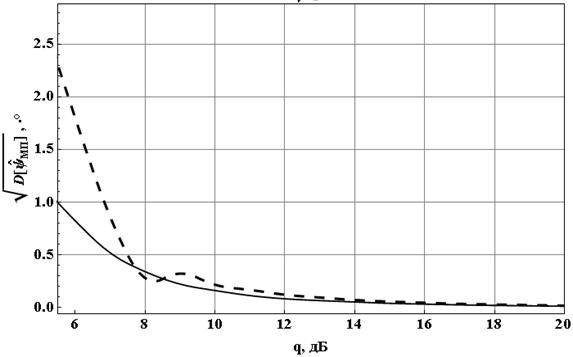
Рис. 4 Корень из рассеяния оценки  для при объёме  выборки 1000 отсчётов (сплошная кривая) и 2000 отсчётов (пунктирная кривая)

 

Рис. 5 Смещение оценки для случаев

 

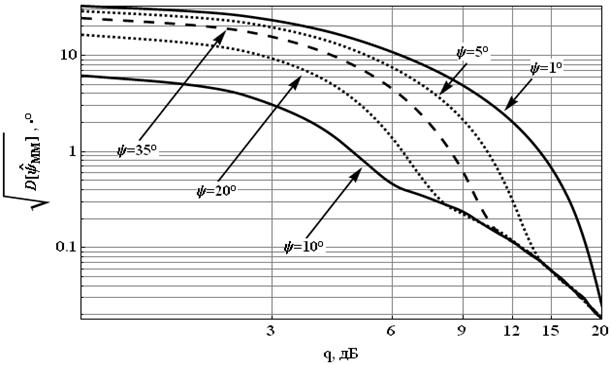
Рис. 6 Рассеяние оценки для случаев

 

На рисунках 5 и 6 представлены смещение и корень из рассеяния оценок, полученных методом моментов, для набора . Из анализа рисунка 5  можно сделать заключение, что получаемая методом моментов оценка  в области малых отношений сигнал/шум обладает существенным смещением, зависящим от . При этом пороговое значение отношения сигнал/шум (назовём его ), при котором смещение становится пренебрежимо мало (например, 1% от максимального значения), монотонно уменьшается с увеличением истинного значения интегральной разности фаз: от 16 дБ при  до 6 дБ при . Из поведения рассеяния оценки видно, что при больших ОСШ оно перестает зависеть от истинной ИФР. Исходя из этого, можно сделать заключение, что в этой области рассеяние будет быстро сходиться к нижней границе Рао-Крамера.

 

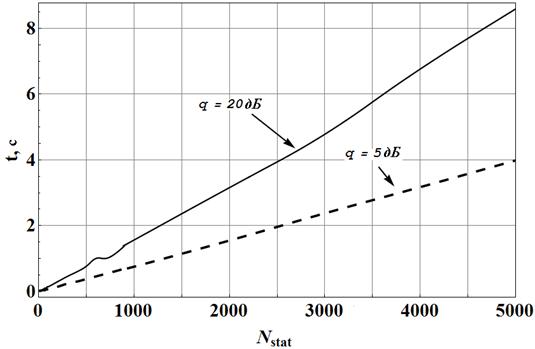
Рис. 7 Время, требуемое для получения МП оценки для случая .

 

При сравнении временных затрат на вычисление максимально правдоподобных и моментных оценок можно отметить, что процедура (7) требует порядка операций, в то время, как количество операций, требуемых при нахождении решения на основе (5), во многом определяется алгоритмом, используемым для решения сопутствующей задачи условной оптимизации. Проведённое моделирование продемонстрировало (см. рисунок 7), что даже наиболее эффективные в вычислительном плане алгоритмы (например, Бройдена–Флетчера–Гольдфарба–Шанно) позволяют произвести оценку за время порядка от нескольких секунд до нескольких десятков секунд, что существенно медленнее, чем при использовании (7), и на практике может являться существенным сдерживающим фактором при принятии решения об использовании данного алгоритма.

 

Заключение

В работе отмечено, что получаемые МП оценки при малых (до 1000 отсчётов) выборках, ОСШ менее 12 дБ и ИРФ до 10° обладают существенным смещением и рассеянием, что делает невозможным применение МП оценок в таких условиях на практике. Проведённый анализ демонстрирует, что увеличение  позволяет улучшить их характеристики. Однако стоит отметить, что это достигается за счёт существенного увеличения времени проведения оценки и снижения быстродействия системы в целом.

Полученная процедура оценивания на основе метода моментов (7) чрезвычайно проста в реализации и не требовательна к вычислительным ресурсам. При этом рост количества операций, затрачиваемых на проведение оценки, с увеличением объёма выборки – линейный, что  чрезвычайно удобно при больших . Важно также отметить, что получаемые ММ оценки ИРФ не зависят от априорного знания величин ОСШ, что является их несомненным преимуществом по сравнению с другими способами оценивания. При больших ОСШ (от 12-14 дБ) ММ оценки будут иметь пренебрежимо малое смещение (асимптотическая несмещённость) и будут быстро сходиться к границе Рао-Крамера – асимптотическому значению (асимптотическая эффективность).

 

Литература

1.     Bennett C., Toomey J. Target classification with multiple frequency illumination // IEEE Transactions on Antennas and Propagation. – 1981. –  Vol. 29, № 2. – P. 352—358.

2.     Пат. 2498339 Российская Федерация, МПК G01S13/00. Способ активной радиолокации / Гончаров О. П., Понькин В.А.; заявитель и патентообладатель Гончаров О. П. (RU). – № 2012107869/07; заявл. 01.03.2012; опубл. 10.11.2013, Бюл. № 31. – 14 с.

3.     Anderson.S.J. Target classification, recognition and identification with HF radar // Proceedings of the NATO Research and Technology Agency Sensors and Electronics Technology Panel Symposium SET-080/RSY17/RFT: «Target identification and recognition using RF systems», 11—13 October, 2004, Oslo, Norway. RTO-MP-SET-080. —  Pp. 1—20.

4.     Gvozdaryev  A. S., Artyomova T. K. Minimum-phase method for the reference estimation of object size in problems of RF holography// Radioelectronics and Communications Systems. 2011. Vol. 54. P. 189-195.

5.     Гвоздарёв А.С., Артёмова Т.К. Способ повышения качества эталонной оценки размеров объектов радиоголографии в условиях малоэлементной антенной решётки // Известия высших учебных заведений России. Радиоэлектроника. 2012. No 1. Стр. 65–74.

6.     Артёмова Т.К., Гвоздарёв А.С., Захаров А.С. Исследование вероятностных характеристик интегральной разности фаз, используемой в эталонных фазовых методах // Вестник ЯрГУ. Серия Естественные и технические науки. 2012. №4, с. 30–36.

7.     Гвоздарёв А.С., Артёмова Т.К., Артёмов К.С. Использование границы Чернова и статистического предела разрешения для определения точности оценки параметров радиоголографических объектов минимально-фазовым методом и построения классификационной сетки эталонов метода // Журнал радиоэлектроники [электронный журнал], 2012. №12. URL: http://jre.cplire.ru/jre/dec12/11/text.pdf

8.     Куликов Е.И., Трифонов А.П. Оценка параметров сигналов на фоне помех. — М. : Сов. радио, 1978. — 296 с.

9.     В. И. Тихонов, Б. И. Шахтарин, В. В. Сизых. Случайные процессы. Примеры и задачи. Том 5. Оценка сигналов, их параметров и спектров. Основы теории информации. — М.: Горячая Линия – Телеком, 2009. — 400 с.

10. Боровков А. А. Математическая статистика — М.: Наука, 1984.

11. Kay S. M. Fundamentals of Statistical Signal Processing. NY: Prentice Hall, 1993. Vol. 1