УДК 621.371.33; 621.396.677.3

РАСЧЕТ ЭНЕРГЕТИЧЕСКИХ ХАРАКТЕРИСТИК ФАЗИРОВАННОЙ АНТЕННОЙ РЕШЕТКИ НАД НЕРЕГУЛЯРНОЙ ЗЕМНОЙ ПОВЕРХНОСТЬЮ МЕТОДОМ ПАРАБОЛИЧЕСКОГО УРАВНЕНИЯ (ТРЕХМЕРНАЯ МОДЕЛЬ)

М. С. Михайлов, В. А. Пермяков, Д. М. Сазонов

Национальный исследовательский университет «МЭИ»

Статья получена 11 декабря 2014 г.

 

Аннотация. Изложена методика расчета энергетических характеристик фазированной антенной решетки (ФАР) над нерегулярной земной поверхностью методом параболического уравнения. ФАР представляет собой периодическую систему однонаправленных излучателей, центры которых лежат в одной плоскости. Диаграмма направленности излучателя в составе ФАР считается известной. Модель земной поверхности — полупространство с переменным в двух направлениях профилем. Предлагаемая методика может быть применена к расчету санитарно–защитной зоны и зоны ограничения застройки в промежуточной и дальней зонах ФАР.

Ключевые слова фазированная антенная решетка, энергетические характеристики, нерегулярная земная поверхность, двумерное параболическое уравнение.

Abstract. A method of calculating the energy characteristics of an phased array antenna above the irregular earth surface by the parabolic equation method is presented. The phased array antenna is a periodic system of unidirectional radiating elements with centers lying in one plane. The radiation pattern of the radiating element embedded into the phased array is assumed to be known and is weakly directional. The model of the earth surface is a half-space with profile varying in two directions. The proposed technique can be applied to calculation of the sanitary-protective zone and the restriction zone of the phased array.

Key words phased array antenna, energetic characteristics, irregular earth surface, two-dimensional parabolic equation.

 

Список сокращений

БПФ — быстрое преобразование Фурье, ГО — геометрическая оптика; ЗОЗ — зона ограничения застройки; ЗП — земная поверхность; МПУ — метод параболического уравнения, ППМ — плотность потока мощности; СЗЗ —санитарно–защитная зона; ФАР — фазированная антенная решетка, РРВ — распространение радиоволн.

Введение

При практическом использовании ФАР, работающих при высоком уровне мощности над ЗП, возникает необходимость расчета ППМ в различных зонах антенны и определение, в соответствии с требованиями санитарно–эпидемиологических правил и норм РФ [1], границ СЗЗ и ЗОЗ. Известны утвержденные в качестве нормативных документов методики расчета СЗЗ и ЗОЗ для антенн над плоской однородной ЗП [2, 3], см. также [4]. В [5] была реализована методика расчета энергетических характеристик ФАР над нерегулярной в одном направлении ЗП на основе МПУ. В настоящей работе рассматривается расчет энергетических характеристик ФАР по МПУ над двумерно нерегулярной ЗП.

Особенности применения МПУ к расчету электромагнитного поля ФАР над земной поверхностью сложной структуры

МПУ в применении к излучению элементарного вибратора над землей был предложен М. А. Леонтовичем [6, 7] и в настоящее время широко применяется в теории дифракции и РРВ [8]. Количество работ по применению МПУ в задачах РРВ велико, поэтому ограничимся ссылками на минимум работ, необходимых для обсуждения методики.

Для антенных решеток и реальных профилей ЗП строгая постановка задачи РРВ требует решения трехмерных векторных уравнений Максвелла или векторного уравнения Гельмгольца. Пусть имеется выделенное направление вдоль ЗП, в котором параметры ЗП медленно меняются по сравнению с изменением в поперечных сечениях. Если излучающие системы создают над ЗП электрическое поле параллельной/перпендикулярной поляризации, в котором доминирует одна декартова компонента, исходные уравнения могут быть сведены к двумерному скалярному ПУ.

Изложим идею МПУ в рассматриваемом нами случае. Рассмотрим скалярное трехмерное уравнение Гельмгольца для функции U (x, y, z):

                                                 ,                                        (1)

В (1) y, z — горизонтальные, x — вертикальная декартовы координаты, и  — волновое число и длина волны в вакууме, ε(x,y,z) — относительная диэлектрическая проницаемость верхнего полупространства ε.

Пусть антенна создает в направлении z>0 поле излучения, которое может быть приближенно представлено в виде

                                         ,                                 (2)

Здесь и далее U — искомая компонента поля, W — комплексная амплитуда поля, используется временной множитель exp(iωt).

После подстановки (2) в (1) и пренебрежения второй производной функции W по переменной z, получим уравнение параболического типа

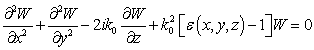                                  ,                          (3)

Уравнение (3) обеспечивает расчет полей антенн в диапазоне углов места до 20^о  (малоугловое приближение) [8]. Другой вариант интегрирования исходного уравнения Гельмгольца сведением к ПУ базируется на применении к (1) метода факторизации [8].

Рассмотрим излучение ФАР над двумерно нерегулярной ЗП. В данной статье приведены численные результаты в пренебрежении вкладами тропосферы и леса. В реализованном алгоритме  учтено отличие диэлектрической проницаемости  среды над землей от 1.

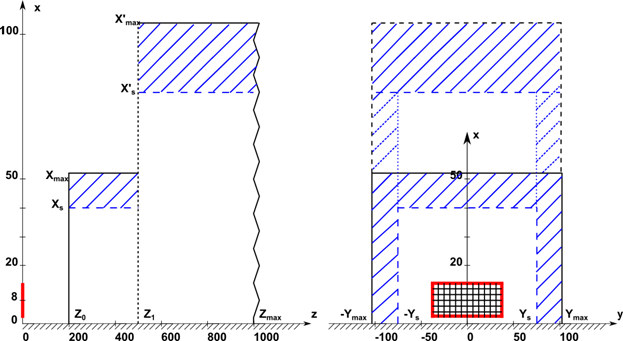
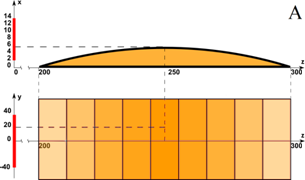
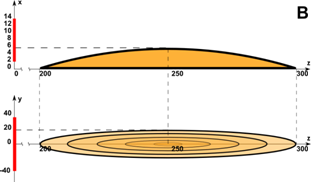
На рис. 1 красным контуром указано положение ФАР в сечении z=0. Математическая постановка задачи для ПУ должна включать начальные условия в сечении Z₀, расположенном правее антенны, и граничные условия на поверхности земли и на бесконечности. При численном решении нужно сделать конечной область расчета в направлении z>Z₀.

 

Рис. 1. К постановке задачи об интегрировании двумерного параболического уравнения.

 

В качестве начального условия в сечении Z₀, параллельном плоскости ФАР, будем использовать амплитудно–фазовое распределение электрического поля, найденное в приближении геометрической оптики с учетом отражения электромагнитной волны, созданной отдельным элементом ФАР, от плоской ЗП. Предполагаемые элементы ФАР — однонаправленные элементы, содержащие вертикальные вибраторы. Методика расчета ЭМ поля для элементарного вибратора над ЗП хорошо известна и очевидным образом обобщается на случай ФАР (см. [9]).

В используемом нами подходе предполагается известной амплитудно–фазовая диаграмма направленности (ДН) элемента ФАР, т.е. начальное условие ставится в дальней зоне элемента ФАР. ДН элемента ФАР может быть задана как независимая функция без учета взаимной связи элементов. Также расчет ДН отдельного излучателя при большом числе элементов ФАР может быть проведен с учетом взаимной связи элементов на модели бесконечной периодической структуры ФАР [10, 11], либо при умеренном конечном числе элементов ФАР с помощью современных электродинамических пакетов типа HFSS, CST Microwave Studio и других.

Такой подход оставляет свободу выбора характеристик элемента ФАР без жесткой привязки к его реальной конструкции. Далее ДН элемента ФАР используется для расчета амплитудно–фазовых характеристик поля ФАР в промежуточной или дальней зоне ФАР.

Размеры промежуточной зоны излучающей системы больших по сравнению с длиной волны размеров определяются неравенством [12]:

                                           (4)

где D — максимальный размер антенны, λ — длина волны, R — расстояние от антенны до точки наблюдения.

Минимальное расстояние, на котором следует рассчитать начальное условие, не должно быть меньше нижней границы промежуточной зоны R_min в том случае, когда ДН элемента задается приближенно, без строгого учета взаимной связи элементов в модели ФАР с конечным числом элементов. При использовании в качестве расчетной модели ФАР с конечным числом элементов также нецелесообразно задавать начальное условие в ближней зоне ФАР, так как вблизи системы излучателей возможны значительные колебания амплитуды поля: появление значительных максимумов и глубоких минимумов поля на расстояниях порядка длины волны и менее [13]. В подобных случаях расчет начального условия и последующее решение ПУ требуется проводить с малым шагом. Таким образом, задание начального условия в промежуточной зоне ФАР является разумным компромиссом, не требующим дальнейшего усложнения алгоритма.

На дальности z>Z₀ профиль ЗП — переменный по двум координатам y и z. Обычно на ЗП задают граничное условие импедансного типа. Однако при расчете полей в промежуточной и дальней зонах ФАР на небольших высотах возможно дальнейшее упрощение граничного условия. Пусть высота элемента ФАР велика по сравнению с длиной электромагнитной волны. Это условие позволяет пренебречь возбуждением земной волны [4, 9]. Предположим также, что расстояние от элемента ФАР до точки наблюдения велико по сравнению с высотой элемента. Это условие соответствует скользящим углам падения плоской волны на ЗП, при которых коэффициент отражения параллельно поляризованной электромагнитной волны можно принять равным минус 1.

Остается решить вопрос о формулировке граничных условий на поверхности, ограничивающей в воздухе область, содержащую основную часть ППМ антенны. На этой поверхности будем использовать поглощающие граничные условия (ПГУ). Область, в которой реализуются ПГУ, выделена штриховкой на рис. 1. В алгоритме предусмотрено увеличение размеров области ПГУ при удалении от антенны, чтобы учесть расширение основного потока мощности антенны.

После формулировки начальных и граничных условий следует выбрать метод решения ПУ. Наиболее широко применяются два метода решения ПУ: конечно–разностный метод  и метод факторизации [8, 14–21]. В настоящей работе использовался метод факторизации с расщеплением (split-step  вариант [8,16]) и двумерное преобразование Фурье по координатам  x,y.

Следует сделать замечание относительно применимости приближения ПУ для расчета ФАР со слабонаправленными элементами. При использованном нами методе ширина ДН элемента может быть увеличена до 60°. В нашей постановке представляет интерес расчет ППМ на малых высотах, ограниченных высотой зданий массовой застройки, т.е. не более 40–80 м. На бо́льших высотах задается ПГУ. С учетом такого ограничения на диапазон высот и выбора ПГУ могут быть проанализированы энергетические характеристики антенн как с узкой, так и с широкой ДН.

В итоге основные моменты методики заключаются в следующем.

1. ФАР задается в виде плоской вертикальной решетки параллельных однонаправленных элементов над плоской ЗП [4,5].

2. Учитывается только вертикальная компонента электрического поля над ЗП, что позволяет ограничиться анализом скалярного ПУ.

3. Начальное условие для интегрирования ПУ находится суммированием полей отдельных излучателей в приближении ГО с учетом отражения плоских волн от плоской ЗП при скользящих углах падения.

4. Граничное условие на ЗП задается при скользящих углах падения коэффициентом отражения электромагнитной волны параллельной поляризации, равным минус 1, а в верхнем полупространстве — с помощью ПГУ.

5. Структура ЗП в области интегрирования задается профилем x=x(y,z). меняющимся в двух направлениях при z>Z₀.

В реализованной методике новыми моментами по сравнению с известными работами являются учет двумерной системы излучателей ФАР и расчет трехмерной структуры поля над двумерно нерегулярной ЗП. Особенностью работы является анализ излучения плоской ФАР с большим числом элементов. Отметим, что ранее в [17] рассматривалась решетка 2×5 вибраторов, при этом использовалось одномерное ПУ. Нами в [5] рассмотрена решетка с 10×10 элементами. Упрощенным по сравнению с общей постановкой остается ПУ, которое полагается скалярным и учитывает только доминирующую — вертикальную компоненту электрического поля.

Верификация программы расчета и численные результаты

Верификация программы расчета поля ФАР в приближении двумерного ПУ для трехмерной модели пространства была проведена путем сравнения с расчетами поля ФАР в приближении ГО и в приближении одномерного ПУ.

Расчет поля ФАР над плоской ЗП. Исходные данные для расчета ФАР приняты следующими. Синфазная вертикальная решетка из 10×100 однонаправленных вибраторных элементов с шагом между элементами 0,5 λ, центр ФАР на высоте 10 м над ЗП, частота 500 МГц. Диаграмма направленности элемента ФАР задавалась функцией sin(θ) при z>0, угол θ отсчитывается от вертикали. Мощность одного элемента 40 Вт, коэффициент усиления 3,28. Начальные условия рассчитывались в приближении ГО на расстоянии 200 м по дальности от плоскости ФАР (при протяженности промежуточной зоны ФАР от 63 м до 3 км). Внутренняя граница ПГУ задавалась по вертикали — на высоте ~40 м, по горизонтали — на расстояниях ±80 м от центра ФАР. Закон изменения мнимой части диэлектрической проницаемости в области ПГУ задавался квадратичной функцией, обращающейся в нуль на внутренней границе поглощающего слоя. Направление излучения ФАР — вдоль ЗП.

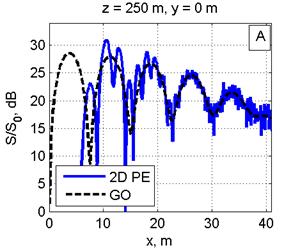
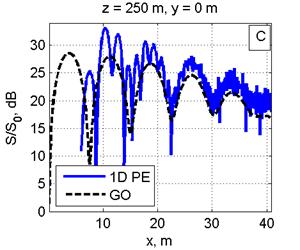
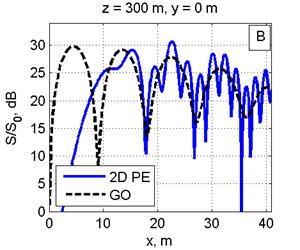
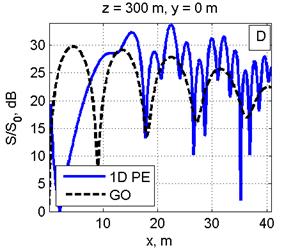
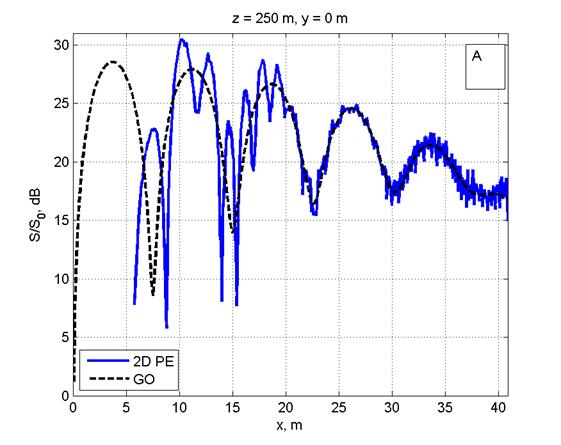
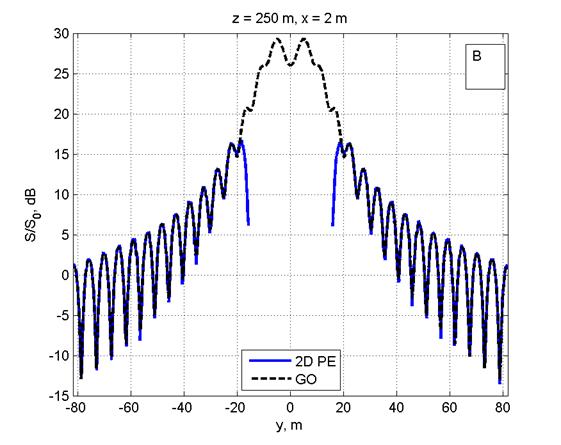
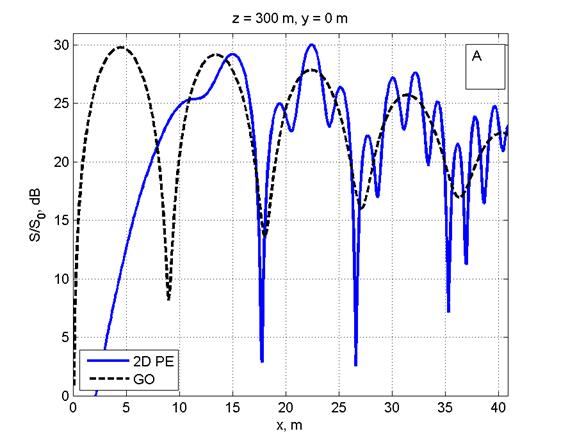
Расчет ППМ (S) в относительных единицах при нормировке на значение 10 мкВт/см² (S₀) проводился на интервале расстояний 200–1000 м 3-мя методами: в приближении ГО [4], с использованием одномерного ПУ для расчета поля от одной вертикальной линейки вибраторов с последующим суммированием полей от всех линеек [5] и прямым интегрированием двумерного ПУ (рис. 2, 3). Шаг в МПУ по высоте и ширине λ/6. Ниже расчеты по ГО оказаны штриховой линией, в приближении ПУ — сплошной линией.

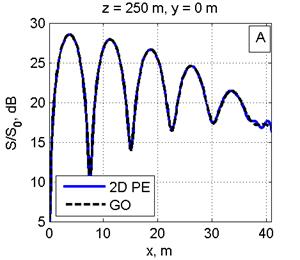
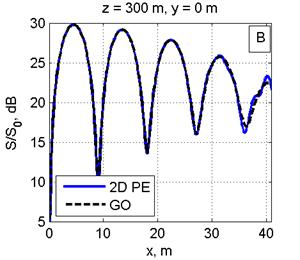
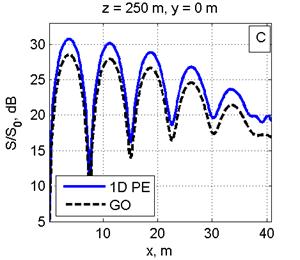
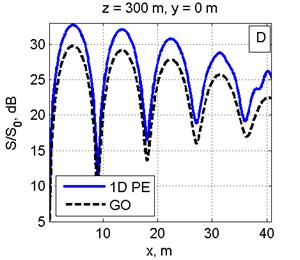
На рис. 2 дано сравнение ППМ, рассчитанных в приближении ГО, с двумерным МПУ (рис. 2А) и одномерным МПУ с суммированием полей от вертикальных линеек вибраторов (рис. 2С) на расстоянии 250 м от ФАР в сечении y=0. Расчеты для расстояния 300 м от ФАР приведены на рис. 2B, 2D.

 

Рис. 2. Распределение ППМ по вертикали в плоскости, перпендикулярной плоскости ФАР и проходящей через ее центр, на дальности 250 м (Рис. 2A, 2С) и 300 м (Рис. 2B, 2D). Слева: сравнение ППМ, рассчитанных  в приближении ГО и по двумерному ПУ(Рис. 2A, 2B). Справа: сравнение приближения ГО с расчетом по одномерному ПУ (Рис. 2C, 2D). Все размеры на рисунках указаны в метрах.
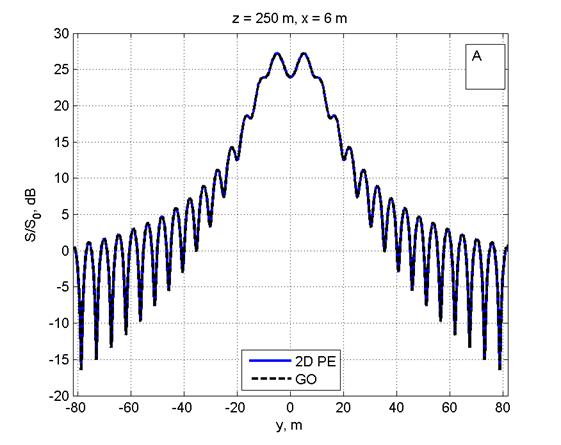
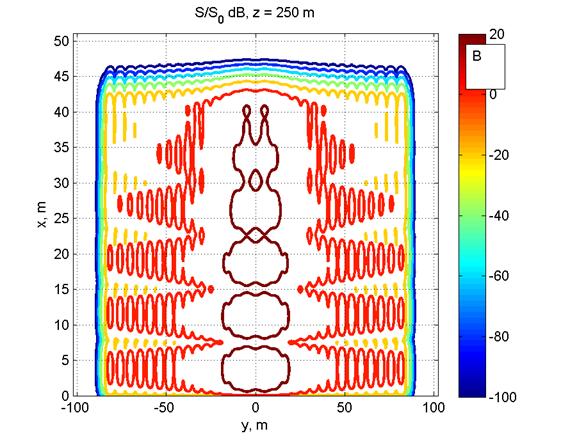
Рис. 3A. Сравнение ППМ, рассчитанных в приближении ГО и по двумерному ПУ, в горизонтальной плоскости, параллельной ЗП, на дальности 250 м от ФАР на высоте 6 м. Рис. 3B: линии уровня ППМ в вертикальной плоскости, рассчитанные по двумерному ПУ, на той же дальности.

Видно графическое согласие расчетов по методу двумерного ПУ с приближением ГО. Одномерный МПУ с увеличением расстояния (рис. 2C, 2D) дает большую погрешность, чем двумерный МПУ(рис. 2A, 2B). Максимальная погрешность расчета по одномерному МПУ не более 2-3 дБ. Вероятно, эта погрешность связана с пересчетом значений поля конкретной линейки вибраторов из цилиндрической системы координат на сетку в прямоугольной системе координат.

На рис. 3A приведено сравнение ППМ, рассчитанных в приближении ГО и по двумерному ПУ в горизонтальной плоскости, параллельной ЗП, на дальности 250 м от ФАР и высоте 6 м. Видно графическое согласие результатов во всей области интегрирования, вплоть до внутренней границы ПГУ (±80 м).

На рис. 3B приведено представление ППМ в виде линий уровня в вертикальной плоскости на дальности 250 м от ФАР. Такое представление, нормированное относительно пороговой ППМ, заданной санитарными нормами, удобно использовать для определения  границ СЗЗ и ЗОЗ.

Расчет ППМ ФАР над ЗП при наличии препятствия. Геометрия двух препятствий — фрагментов цилиндра и эллипсоида вращения показана на рис. 4, расчеты ППМ — на рис. 5–8. Везде на рис. 5–8 сплошной линией показаны расчеты ППМ по МПУ при наличии препятствия, штриховой — в приближении ГО без препятствия.

 

Рис 4. Геометрические размеры нерегулярности на поверхности Земли

 

Влияние цилиндрического препятствия на распределение ППМ по вертикали на расстоянии 250 м от ФАР показано на рис. 5A (расчет по двумерному МПУ) и на рис. 5C (расчет по одномерному МПУ). Видно, что расчеты по одномерному и двумерному МПУ согласуются друг с другом. Влияние препятствия проявляется в усложнении интерференционной структуры поля, увеличении амплитуды и уменьшении периода осцилляций.   «Быстрые» осцилляции на рис. 5A, С на высоте свыше 20 м обусловлены большим шагом по дальности (1 м) и при уменьшении шага на порядок резко ослабляются. При выходе за пределы нерегулярности на дальности 300 м (рис. 5B, D) и далее  таких осцилляций не наблюдается.

 

Рис. 5. Распределение ППМ по вертикали над цилиндрическим препятствием на расстояниях 250 и 300 м от ФАР. Рис 5A, 5B — расчет по двумерному ПУ, рис C,D — расчет по одномерному ПУ с суммированием полей от линеек (сплошные линии). Штриховыми линиями показаны распределения поля над плоской землей в приближении ГО.
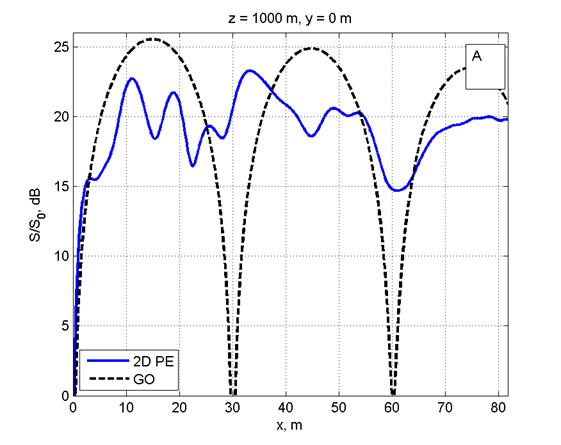
Рис. 6. Распределение ППМ над препятствием эллиптической формы по вертикали (рис. 6A) и по горизонтали на высоте 2 м (рис. 6B) на дальности 250 м от ФАР.

 

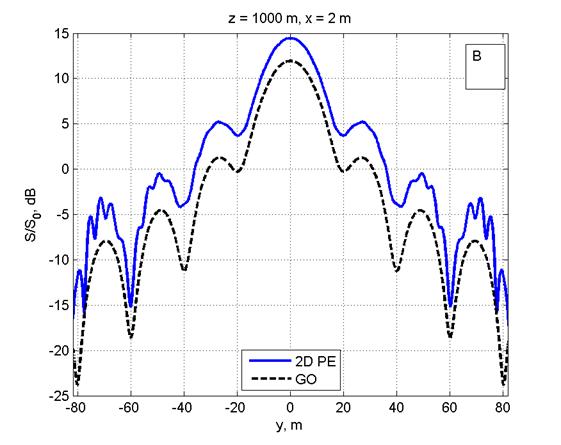
Рис. 7. Распределение ППМ над препятствием эллиптической формы по вертикали (рис. 7A) и по горизонтали на высоте 2 м (рис. 7B) на дальности 300 м от ФАР.

 

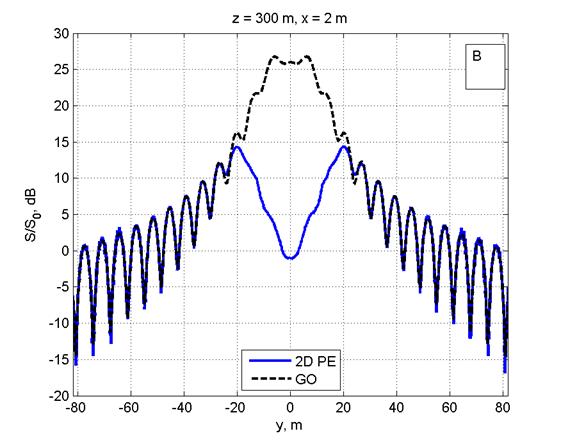
Рис. 8. Распределение ППМ над препятствием эллиптической формы по вертикали (рис. 8A) и по горизонтали на высоте 2 м (рис. 8B) на дальности 1000 м от ФАР.

На рис. 6–8 показано распределение ППМ по вертикали (верхние рисунки) и в горизонтальной плоскости (нижние рисунки) на дальностях соответственно 250, 300 и 1000 м при излучении ФАР над препятствием эллиптической формы. Расчеты в приближении двумерного ПУ (сплошная линия) сопоставлены с приближением ГО над плоской землей (штриховая линия).

Из рис. 6‑8 следует, что интерференционная структура поля над ЗП с препятствием усложняется вследствие дополнительного рассеяния поля на препятствии. В пределах препятствия поле отсутствует (рис. 6), а при удалении от него в направлении от ФАР наблюдается глубокий минимум ППМ (рис. 7), постепенно замываемый эффектами дифракции (рис. 8).

На базе реализованного метода были проведены также расчеты ППМ ФАР с учетом влияния лесного массива конечных размеров. Данные расчеты будут рассмотрены в отдельной публикации.

Заключение

Предложена и программно реализована методика расчета напряженности электрического поля и плотности потока мощности плоской ФАР, расположенной над двумерно нерегулярной земной поверхностью. Излучатели ФАР — однонаправленные вибраторные элементы, лежащие в плоскости ФАР. Вертикальная компонента электрического поля ФАР находится путем решения двумерного ПУ с применением двумерного БПФ. ДН элемента ФАР считается известной, начальное условие для ПУ находится  методом ГО над плоской землей в промежуточной зоне ФАР.

Методика может быть использована для расчета СЗЗ и ЗОЗ вблизи ФАР при высоком уровне излучаемой мощности. Аналогично подходу, использующему одномерное ПУ [5], предложенная методика позволяет учесть неоднородность  тропосферы,  лесные массивы, сферичность Земли.  Также возможно обобщение методики для более сложных излучателей ФАР. Наконец, использование результатов работ Д.М.Сазонова [22,23] позволяет обобщить предложенную методику на случай ФАР произвольной геометрии, расположенных над двумерно нерегулярной ЗП.

Работа выполнена при финансовой поддержке Государственного задания в сфере научной деятельности в проектной части №8.152.2014/К.

 

Литература

1. Государственное санитарно–эпидемиологическое нормирование Российской Федерации. Государственные санитарно–эпидемиологические правила и нормативы. 2.1.8. Физические факторы окружающих природных сред. 2.2.4. Физические факторы производственной среды. Гигиенические требования к размещению и эксплуатации передающих радиотехнических объектов. Санитарно–эпидемиологические правила и нормативы СанПиН 2.1.8./ 2.2.4.1383–03 (с изменениями от 19 декабря 2007 г.).

2. Методические указания МУК 4.3.043–96. Определение плотности потока мощности электромагнитного поля в местах размещения радиосредств, работающих в диапазоне частот 700 МГц – 30 ГГц. Госсанэпиднадзор, 1996 г.

3. Методические указания МУК 4.3.1677–03. Определение уровней электромагнитного поля, создаваемого излучающими техническими средствами телевидения, ЧМ радиовещания и базовых станций сухопутной подвижной радиосвязи. Минздрав России, 2003 г.

4. Пермяков В. А., Михайлов М. С. Расчет энергетических характеристик активной фазированной антенной решетки над плоской земной поверхностью. / Радиотехника , 2013, №10, с. 83–88.

5. Пермяков В. А., Михайлов М. С. Расчет энергетических характеристик активной фазированной антенной решетки над нерегулярной земной поверхностью методом параболического уравнения. // Доклады I Всероссийской микроволновой конференции, 27–29 ноября 2013 г., Москва, с.289‑293.

6. Леонтович М. А. Об одном методе решения задач о распространении электромагнитных волн вдоль поверхности земли. / Известия АН ССР, сер. физ., 1944, т.8, № 1, с. 16.

7. Леонтович М. А., Фок В. А. Решение задачи о распространении электромагнитных волн вдоль поверхности земли по методу параболического уравнения. // ЖЭТФ, 1946, т. 16, вып.7, с. 557–573.

8. M. Levy. Parabolic equation methods for electromagnetic waves propagation. London, UK, IEE, 2000.

9. Фейнберг Е. Л. Распространение радиоволн вдоль земной поверхности. –М.: АН СССР, 1961.

10. Амитей Н., Галиндо В., Ву Ч. Теория и анализ фазированных антенных решеток. –М.: МИР,1974, –455 с.

11. Бодров В. В., Марков Г. Т. Возбуждение периодических антенных решеток. //Сб. научно – методических статей по прикладной электродинамике. М.: Высшая школа, вып.1, 1977, с. 129-162.

12. Марков Г. Т., Сазонов Д. М. Антенны. Учебник для студентов радиотехнических специальностей вузов. Изд. 2-е. –М.: Энергия, 1975, 528 с.

13. Пермяков В. А., Корюкин А. Н., Михайлов М. C., Сороковик Д. В. О формировании областей с малым значением электрического поля на конечном расстоянии от системы излучателей // Журнал радиоэлектроники [электронный журнал].  2013. №7. Режим доступа: http://jre.cplire.ru/jre/jul13/ 3/text.pdf

14. A. E. Barrios. Advanced Propagation Model (APM) Computer Software Configuration Item (CSCI) Documents./D. R. Sailors, A. E. Barrios, W. L. Patterson, H. V. Hitney // Technical document 3033, August 1998.

15. CARPET (Computer–Aided Radar Performance Evaluation Tool).    [Электронный ресурс]. — Режим доступа:

www/URL: http://www.tno.nl/downloads/carpet.pdf

16. D.J. Thomson, N.R. Chapman. A wide–angle split–step algorithm for the parabolic equation.  // J. Acoust. Soc. Amer. 2000, vol.74, pp. 1848–1854.

17. Gokhan Apaydin, Levent Sevgi. A Novel Split–Step Package for Surface–Wave Propagation Prediction along Multiple Mixed Irregular–Terrain Parts. // IEEE Antennas and Propagation Magazine, vol. 52, No. 4, Aug. 2010, pp. 90–96.

18. Ахияров В. В. Метод параболического уравнения в теории дифракции. // Успехи современной радиоэлектроники, 2010, №9, с.72–80.

19. Ахияров В. В. Вычисление множителя ослабления над земной поверхностью методом параболического уравнения. // Журнал радиоэлектроники [электронный журнал]. 2012.  № 1. URL: http://jre.cplire.ru/jre/jan12/16/text.pdf.

20. Ахияров В. В. Результаты решения скалярных задач излучения и дифракции методом параболического уравнения. // Электромагнитные волны и электронные системы. 2014. Т. 19. № 2. С. 12–18

21. Gokhan Apaydin, Levent Sevgi. Ground wave propagation at short Ranges and Accurate Source Modelling. // IEEE AP Magazine, vol. 55, No. 3, June 2013, pp.244–262.

22. Сазонов Д. М. Теория антенных решеток произвольной геометрии. Дисс. на соискание ученой степени д.т.н., –М.: МЭИ, 1970 г.

23. Сазонов Д. М. Матричная теория антенных решеток. – Таганрог, изд. ЮФУ, 2013, 96 с.