УДК 539.371, 538.911
СОБСТВЕННОЕ ИЗЛУЧЕНИЕ И КОЭФФИЦИЕНТ ОТРАЖЕНИЯ ЭМВ В ДИАПАЗОНЕ 8 ММ СПЛАВОВ Ni2,14Mn0,81GaFe0,05 И TiNi В ТЕМПЕРАТУРНОМ ИНТЕРВАЛЕ ВБЛИЗИ ФАЗОВЫХ ПЕРЕХОДОВ
1-ГО и 2-ГО РОДА
И. В. Бычков1, В. А. Голунов2, Д. С. Каленов2, А. П. Каманцев3, Д. С. Кучин3, В. В.
Коледов3, Д. А. Кузьмин1, В. В. Мериакри2,
С. В. фон Гратовски2, М.
П. Пархоменко2, А. В. Маширов3, В. Г. Шавров3
1 Челябинский государственный университет
2 ИРЭ им. В. А. Котельникова РАН, Фрязинский филиал
3 ИРЭ им. В.А. Котельникова РАН, Москва
Статья получена 1 декабря 2014 г.
Аннотация. Созданы оригинальные экспериментальные методики для изучения электромагнитного отклика и самопроизвольного (квазитеплового) излучения ЭМВ в диапазонах 28-32 ГГц образцов твердых тел с фазовыми превращениями (ФП). С помощью этих методик проведены in situ измерения, собственного электромагнитного излучения образцов ферромагнитного сплава Гейслера Ni2,14Mn0,81GaFe0,05 и сплава Ti-Ni c термоупругими мартенситными ФП. Для образца Ni2,14Mn0,81GaFe0,05 методом одновременного измерения квазитеплового излучения радиометрическим методом (в диапазоне 28-32 ГГц) и одновременные измерения низкочастотной магнитной восприимчивости, отражающей протекание магнитного и структурного ФП в образце обнаружена аномальная немонотонная зависимость излучения от температуры вблизи магнитоструктурного ФП 1-го рода (330 – 345 К) и аномальные флуктуации излучения вблизи точки Кюри (360 К). Разделены вклады в сигнал радиометра от собственного излучения образца и отраженного электромагнитного фона. Влияние кинетики ФП на характер миллиметрового излучения образца изучались при изменении скорости нагрева/охлаждения от 0,1 К/с до 10 К/с. Показано, что пики собственного излучения возрастают при увеличении скорости изменения температуры. Эти данные подтверждают гипотезу о том, что обнаруженные аномалии не подчиняются формуле Планка и закону Стефана-Больцмана и связаны с неравновесными процессами при ФП. В сплаве TiNi с термоупругим мартенситным ФП исследовано радиометрическим методом собственное излучение и коэффициент отражения ЭМВ в диапазоне 28 - 32 ГГц. В интервала температур вблизи ФП (290 – 315 К) обнаружены аномалии собственного излучения и коэффициента отражения, связанные с неравновесными процессами при ФП. Предложена модель, связывающая аномалии коэффициента отражения и интенсивности собственного излучения, проведено численное моделирование и получено качественное согласие расчетных и экспериментальных результатов.
Ключевые слова: ЭМВ, фазовый переход, миллиметровые волны, сплавы Гейслера, Ti-Ni, собственное излучение, коэффициент отражения.
Abstract. The original experimental techniques are created for the study of the electromagnetic response and spontaneous radiation of electromagnetic waves in the range of 28-32 GHz, of samples of the alloys with phase transitions (PT). Using these techniques, the following experiments were done: there were carried in situ measurements of the electromagnetic waves radiation of a ferromagnetic Heusler alloy Ni2,14Mn0,81GaFe0,05 by radiometry techniques (in the range of 28-32 GHz), and simultaneously measuring of the low-frequency magnetic susceptibility, reflecting the occurrence of magnetic and structural PTs in the sample. An anomalous no monotonic temperature dependences of the radiation in the temperature range near magneto structural PT of the 1st order (330 - 345 K), and abnormal fluctuations in the radiation near the Curie point (360 K) were detected. The contributions to the signal from the self-radiation of the sample and the reflected electromagnetic radiation from a background were separated. The influence of the nature of the kinetics of PT upon millimeter wave radiation of sample was investigated by changing the rate of heating / cooling from 0.1 K / s to 10 K / s. It was shown that the peaks of the intrinsic radiation increases with the rate of temperature change. These methods confirm that the detected anomalies are not subjected to Planck's formula and the Stefan-Boltzmann law and are associated with non-equilibrium processes at PT. The study by the radiometric technique of the electromagnetic radiation of the TiNi alloy of it’s intrinsic radiation and electromagnetic wave reflection coefficient in the range of 28-32 GHz were done. In the temperature range near the thermoelastic martensitic structural PT (290-315 K) there were revealed the anomalies of the intrinsic radiation and the reflection coefficient which are associated with the non-equilibrium processes at PT. The model is propose that relates the reflection coefficient anomalies and intensity of intrinsic radiation. The results of numerical simulations are in good qualitative agreement with the experimental data.
Keywords: electromagnetic waves, millimeter range, phase transition, shape momery effect, TiNi, Heusler alloys, reflection coefficient, intrinsic radiation, evanescent modes.
Введение
Спиновая калоритроника быстро формируется в самостоятельную дисциплину, о чем говорят статьи и обзоры [1-27], появившиеся в последнее время. В этих, работах, как правило, изучаются спиновые и спин - поляризованные туннельные токи в твердотельных слоистых структурах металл-металл, и металл-диэлектрик при тепловых градиентах. В них показано, что тепловой поток может сильно влиять на спиновый и зарядовый транспорт в полупроводниках, диэлектриках, металлах и полуметаллах. Однако, независимо, начиная с 2000-х годов развивается физика и технология вакуумных туннельных структур, в которых разность температур в вакуумном промежутке вызывает появление туннельного тока, который, как полагают, в свою очередь может при сильном градиенте температур обеспечить генерацию высокой удельной мощности электрической энергии и служить источником электроэнергии с высокими параметрами эффективности, как раз за счет того, что теплопередача в вакууме сильно подавлена [28-31].
Вакуум не является идеальным теплоизолятором. Классическая теория теплопроводности исходит из того, что обмен энергии в вакууме происходит за счет излучения фотонов. На основе статистической радиофизики она развита в [17] и усовершенствована в [19]. Проведенные в самое последнее время экспериментальные исследования теплопроводности между поверхностями твердых тел на малых расстояниях, показывают существенные превышения значений, рассчитанных для абсолютно черного тела. Эти данные находят объяснение в рамках учета эванесцентных мод, убывающих вблизи поверхности [11]. Необходимо также учитывать возможность туннелирования фононов между поверхностями, так как электромагнитные и упругие возбуждения в твердом теле связаны между собой. На микро и наноуровне взаимодействие колебательных подсистем твердых тел может осуществляться за счет сил Ван-дер-Ваальса и Казимира.
1. Постановка задачи и цель исследования
В настоящей работе экспериментально изучается излучение магнитных и немагнитных твердых тел с фазовыми переходами (ФП), на которое может оказать влияние связь подсистем и неустойчивость фаз под действием температуры и проводится поиск новых эффектов неравновесного характера излучения. Однако, собственное излучение тел, сопровождающее ФП, так называемое фазопереходное излучение – довольно общее физическое явление, которое приходится учитывать даже в космологии для описания происхождения энергетических потоков во вселенной [24]. В течение многих лет фазопереходное излучение, сопровождающее ФП 1-го рода при конденсации, кристаллизации, сублимации воды исследуется физиками для объяснения многочисленных явлений в атмосфере земли, инфракрасного излучения земной поверхности и облаков [24]. Оно замечено в виде пиков спектра ИК излучения, которые наблюдаются в процессе роста кристаллов различного химического состава [23]. Иногда интенсивность излучения в пиках на 2-3 порядка превышает расчетную интенсивность теплового излучения по формуле Планка для этой частоты. В [22] делаются следующие физические оценки для частоты ω фазопереходного излучения в процессе конденсации водяного пара (ФП 1-го рода):
ħω = L/NА, (1)
где ħ – постоянная Планка, L – молярная скрытая теплота ФП, NА – число Авогадро. Для конденсации воды из пара длина волны фазопереходного излучения – 2,9 мкм, для замерзания воды – 39,2 мкм. Эксперимент подтверждает расчеты [21, 26]. Однако, изученный для ряда диэлектрических кристаллов и жидкостей, например воды, для случая мартенситных фазовых переходов в металлах, этот эффект, до сих пор, по-видимому не исследовался. При исследовании вакуумной теплопроводности между поверхностями кристаллов с мартенситным ФП можно ожидать появление эффектов излучения с частотой, определяемой описанной выше формулой, но пропорционально молярной скрытой теплоте перехода, меньшей частотой (на 2 порядка ниже, чем при конденсации воды, то есть в субмиллиметровой области ЭМВ).
Цель данной работы заключается в том, чтобы изучить собственное излучение и аномалии коэффициента отражения ЭМВ от образцов ферромагнитного сплава Гейслера Ni2,14Mn0,81GaFe0,05 и неферромагнитного сплава TiNi вблизи ФП 1-го и 2-го рода в диапазоне 28-32 ГГц.
2. Образцы и методы
Поликристаллические образцы сплава Гейслера Ni2,14Mn0,81GaFe0,05 с магнитоуправляемым эффектом памяти формы были изготовлены методом дуговой плавки в атмосфере аргона на холодном поду и подвержены гомогенизирующему отжигу в течение 50 часов при температуре 1073 К. Технология изготовления сплавов, их структура и физические свойства подробно описаны в [32-35]. В сплаве Ni2,14Mn0,81GaFe0,05, как известно, между 0 и 100 оС наблюдаются два ФП: Точка Кюри (Тс = 360 К и термоупругое мартенситное превращение 1-го рода с температурным гистерезисом в интервале 330 – 345 К).
Образцы почти эквиатомного сплава TiNi – серийные производства ЗАО «МАТЭКС». Измерения методом дифференциальной сканирующей калориметрии показали наличие мартенситного перехода с характерными температурами начала и конца мартенситного перехода: Ms = 303 К, Mf = 288 К, As = 323К , Аf = 333 К.
Для измерения коэффициента отражения образцов вблизи ФП использовался стандартный панорамный измеритель КСВН серии Р-2 с прямоугольными стандартными волноводами на частотах 28 - 32 ГГц. Для решения задачи об измерении собственного излучения образца сплава в вакуум или воздушную среду создана установка, которая предназначена для одновременного измерения излучения СВЧ и намагниченности образцов сплавов при термоциклировании в температурном интервале от 0 до 120 оС.
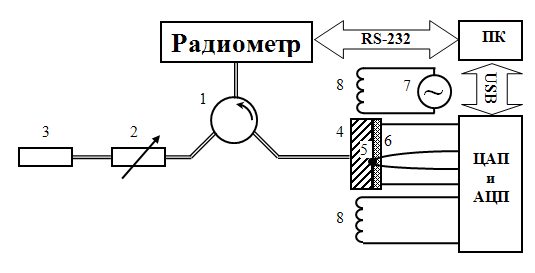
Установка (см. схему на Рис. 1) состоит из соединённых стандартными прямоугольными волноводами: прибора для измерения интенсивности ЭМФ на длинах волн 8 мм (радиометр), циркулятора (1), аттенюатора (2), нагрузки (3), поддерживаемой при температуре кипящего азота, образца (4) с прикрепленной к нему термопарой (5) и находящегося в тепловом контакте с элементом Пельтье (6), а также генератора звуковой частоты (7), и трансформаторного датчика магнитной восприимчивости (8).
|
Рис. 1. Схема экспериментальной установки для исследования собственного излучения образца вблизи ФП в диапазоне 8 мм. |
|
|
Установка работает следующим образом. Не только образец (4), но и радиометр являются источниками квазитеплового излучения. Тепловое излучение, генерируемое радиометром, подается в волновод и попадает через циркулятор (1) на холодную нагрузку (3). В нагрузке излучение поглощается, а излучение охлаждаемой нагрузки менее интенсивное, чем излучение нагретого
радиометра попадает на образец (4) через циркулятор (1). Вводя в систему аттенюатор (2) можно регулировать соотношение между тепловым «холодным» и «теплым» СВЧ излучением, попадающим на образец. Далее излучение падает
на образец и, частично отражаясь от него, попадает обратно в радиометр. Кроме того, в радиометр попадает собственное излучение образца.
Для измерения магнитной восприимчивости применена простая трансформаторная схема. Электрический сигнал с частотой 1,7 кГц от генератора (7) поступает на первичную катушку (8) трансформатора магнитометра. Сигнал снимается со вторичной катушки трансформатора, сердечником которой является образец сплава. Таким образом, по величине выходного сигнала можно определить магнитную восприимчивость образца (4), расположенного между катушками индуктивности одновременно с измерением СВЧ сигнала, включающего компоненту собственного излучения и излучение, отраженное его поверхностью. Температура образца может меняться в диапазоне от 0 до 100 оС за счет присоединенного к нему элемента Пельтье (6). Измерение температуры производится термопарой (5), а также миниатюрным диодным датчиком, расположенным непосредственно на поверхности образца со стороны волновода (на схеме не показан). Процесс измерения полностью автоматизирован. Управление осуществляет персональный компьютер (ПК) посредством платы цифро-аналогового и аналого-цифрового преобразователя (ЦАП и АЦП).
Измеряемое радиометром излучение позволяет определить яркостную температуру образца Т. Вклад в излучение, которое характеризуется яркостной температурой Т, вносит собственное излучение образца и излучение, отраженное от него:
T = æ·Tобр. + R·T*, (2)
где æ – коэффициент пропускания, R – коэффициент отражения, Тобр. – термодинамическая температура образца, T* – температура подсветки.
По закону сохранения энергии коэффициенты æ и R связаны соотношением:
æ + R = 1. (3)
Используя соотношения (2) и (3) получим:
T = æ·Tобр. + R·T* = (1 – R)· Tобр.+RT* = Tобр.- R(Tобр. – T*) (4)
Выражение (4) раскрывает принципиальную возможность разделения вкладов в показание радиометра от собственного излучения образца и отраженного от него. Регулируя в эксперименте интенсивность подсветки T*, возможно с помощью радиометра измерить как собственное излучение образца, так и суммарный сигнал, обусловленный изменением температуры образца и температурной зависимостью его коэффициента отражения вблизи ФП.
3. Эксперимент
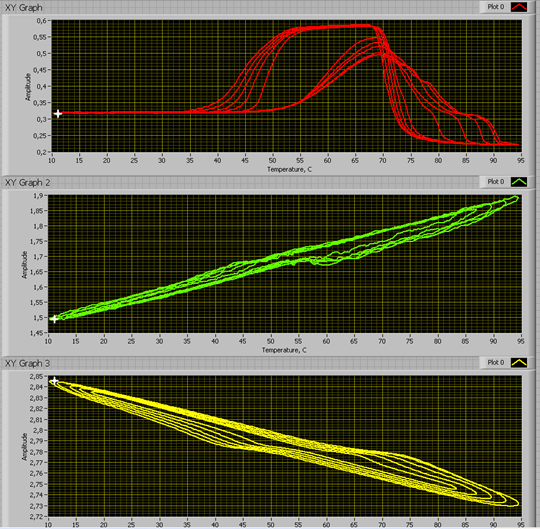
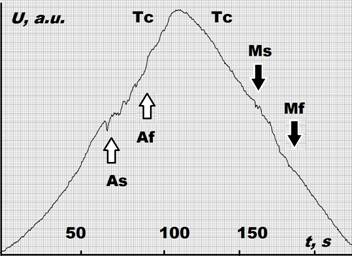
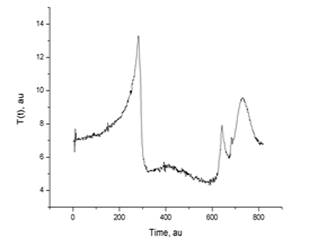
Ниже приводятся предварительные экспериментальные данные по исследованию собственного квазитеплового излучения сплавов Ni2,14Mn0,81GaFe0,05 и Ti-Ni с ФП, полученные на описанной выше установке. На Рис. 2 представлена серия зависимостей снятых in situ – одновременно: намагниченности образца от температуры (красная кривая), показаний радиометра (зеленая кривая) и показаний миниатюрного термодатчика (желтая кривая), расположенного в волноводе радиометра, прикасающегося к поверхности образца. На зависимости магнитной восприимчивости хорошо видны аномалии, связанные с точкой Кюри (резкое возрастание сигнала) и с мартенситным структурным переходом 1-го рода (снижение магнитной восприимчивости образца при переходе из высокотемпературной фазы - аустенита в низкотемпературный мартенсит). Показания радиометра регистрируют связанные с мартенситным ФП немонотонные аномалии собственного излучения (зеленые кривые). Отдельно график временной зависимости сигнала радиометра при циклическом нагреве/охлаждении образца показан на графике Рис. 3. Видны немонотонные аномалии вблизи температурных областей начала и конца прямого и обратного мартенситного перехода: Ms = 323 К, Mf = 313 К, As = 323 К, Af = 337 К и точки Кюри ТС = 345 К. Зависимости показаний радиометра от температуры при скоростях нагрева/охлаждения 2 и 5 К/с показаны на Рис. 4 и 5, соответственно.
|
|
|
Рис. 2. Эксперименты in situ по одновременному исследованию намагниченности образца сплава Ni2,14Mn0,81GaFe0,05 и его магнитной восприимчивости в зависимости от температуры. (По оси абсцисс – температура С, по оси ординат – магнитная восприимчивость в отн. ед (красная кривая), сигнал радиометра в отн. ед. (зеленая кривая) и сигнал от микродатчика температуры (тероморезистора) установленного в резонаторе, в непосредственном контакте с образцом (желтая кривая).
|
|
|
|
Рис. 3. Типичный график временной зависимости собственного излучения образца сплава Гейслера Ni2,14Mn0,81GaFe0,05 при термоциклировании от 0 до 100 °С, полученной при помощи радиометра. Видны немонотонные аномалии вблизи температурных областей начала и конца прямого и обратного мартенситного перехода: Ms = 323 К, Mf = 313 К, As = 323 К, Af = 337 К и точки Кюри ТС = 345 К.
|
|
|
|
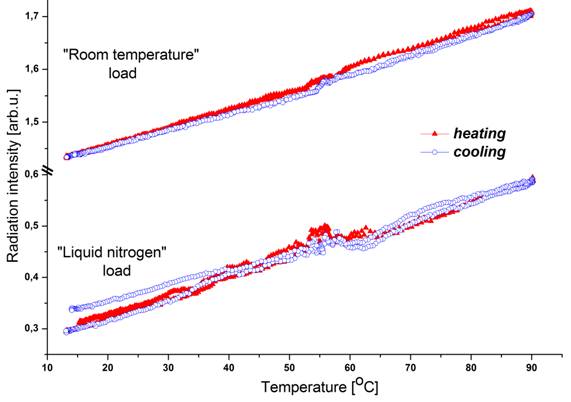
Рис. 4. Зависимости интенсивности собственного излучения образца Ni2,14Mn0,81GaFe0,05 от температуры при скорости нагрева/охлаждения 2 К/с. |
|
|
|
Рис. 5. Зависимости собственного излучения образца Ni2,14Mn0,81GaFe0,05 от температуры при скорости нагрева/охлаждения 5 К/с.
|
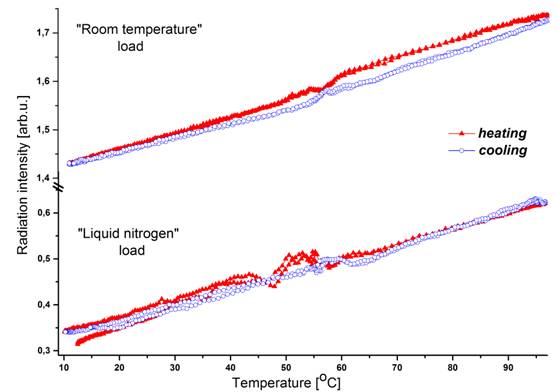
Нижние кривые на рисунках соответствуют выключенному аттенюатору (подключена нагрузка при температуре жидкого азота), а верхние – полностью включенному аттенюатору (нагрузка имеет комнатную температуру).
По данным на Рис. 4 можно определись, что зависимость излучения образца от температуры имеет немонотонную зависимость (нижние кривые). Особенности на кривых, по-видимому, можно объяснить происходящим в образце фазовым мартенситным превращением, а температуры этих особенностей совпадают с соответствующими температурами роста и спада намагниченности на Рис. 2. Однако механизм появления такой зависимости до конца не ясен. Необходимо разделить два основных вклада: собственное излечения при ФП и изменение коэффициента отражения фонового излучения при смене фаз. В соответствии с формулой (4) можно предположить, что немонотонность интенсивности излучения возникает вследствие зависимости коэффициента отражения от температуры образца. Кроме того, чем больше разность (Tобр. – T*), тем более эта зависимость должна быть выражена на кривых излучения. Действительно, при включении аттенюатора (увеличении Т*) разность (Tобр. – T*) уменьшается, и немонотонность на кривых практически пропадает (верхняя кривая на Рис. 4). Однако вызывает интерес тот факт, что при более высокой скорости термоциклирования образца, немонотонность (пик) остается даже при Т* равной комнатной (при включенном аттенюаторе) (верхняя кривая на Рис. 5). Таким образом, имеет место кинетический эффект выделения (поглощения) излучения. Это может быть объяснено вкладом от собственного неравновесного излучения образца при ФП. При большей скорости термоциклирования собственное излучение образца (остающееся неизменным) дает больший вклад в суммарное излучения. В то время как энергия теплового излучения Q (при неизменной мощности W) вносит меньший вклад за счет уменьшения времени t регистрирования сигнала (Q = W·t).
Полученные экспериментальные данные позволяют высказать гипотезу о существовании двух составляющих излучения регистрируемого радиометром от образца: собственное излучение и отраженное излучение. Созданная установка, позволяет изучить каждый из вкладов в отдельности. Показано, что вклад от собственного излучения увеличивается при увеличении скорости термоциклирования образца. Таким образом, собственное излучение имеет неравновесный кинетический характер, и возможно связано не только с температурой образца напрямую, но и с выделением скрытой теплоты в процессе ФП.
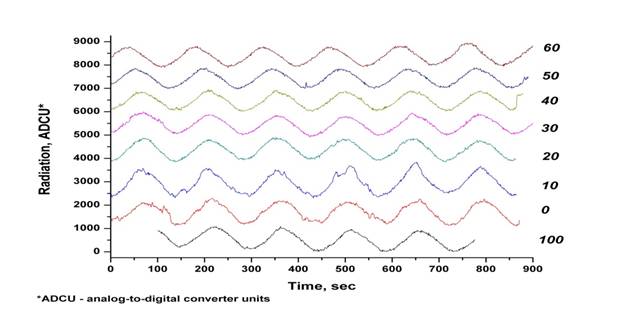
Рис. 6 показывает семейство временных зависимостей сигнала радиометра при термоциклировании образца сплава Ni2,14Mn0,81GaFe0,05 вблизи магнитного ФП 2-го рода (точки Кюри). Параметром служит эффективная температура излучения подсветки от 0 до 100 % (уровень поглощения аттенюатора). Специфические флуктуации наблюдаются вблизи ФП при низкой температуре подсветки (0 и 10 процентов показаний аттенюатора (столбец справа). Временные параметры флуктуаций – характерное время – порядка 1 сек. Интенсивность на уровне 10 – 20 процентов от средней величины теплового излучения.
|
|
|
Рис. 6. Временные зависимости сигнала радиометра при термоциклировании образца вблизи магнитного ФП - 2 го рода (точки Кюри). Параметром служит эффективная температуры излучения подсветки. Флуктуации наблюдаются вблизи ФП при низкой температуре подсветки (0 и 10 % показаний аттенюатора). |
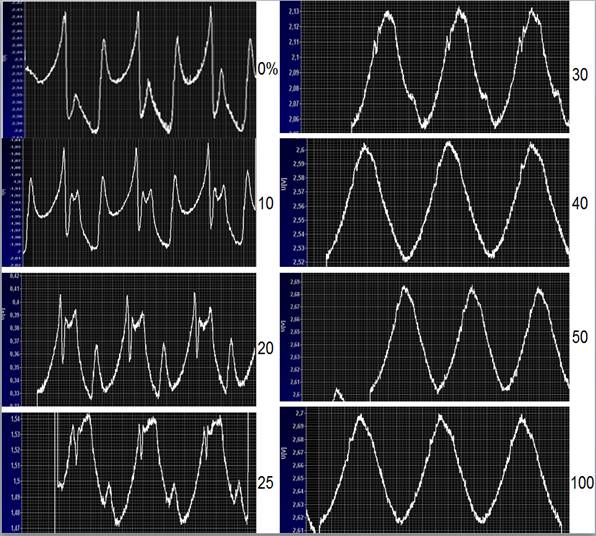
Эксперименты были продолжены на образцах немагнитного сплава Ti-Ni с термоупругим мартенситным ФП. Отличие методики заключалось в том, что не проводились измерения магнитной восприимчивости. Измерения интенсивности собственного излучения радиометрическим методом дополнены измерением температурной зависимости коэффициента отражения в диапазоне 28 - 32 ГГц. На Рис. 7. Показано семейство временных зависимостей сигнала радиометра для сплава Ti-Ni. Наблюдаются яркие аномалии сигнала от радиометра при термоциклировании в районе мартенситного ФП первого рода.
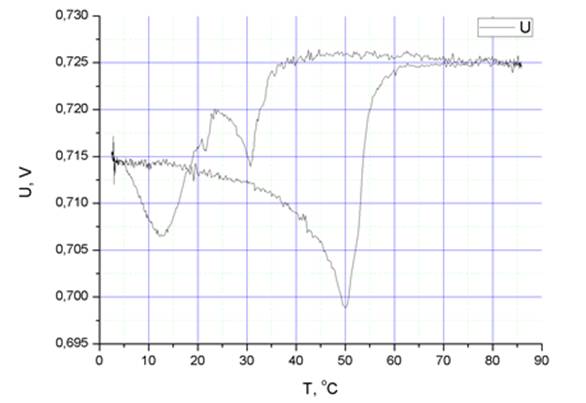
На Рис. 8 показана зависимость коэффициента отражения этого же образца полученная с помощью панорамного измерителя КСВН. Зависимость имеет гистерезисную аномалию вблизи ФП первого рода.
Для интерпретации температурных зависимостей показаний радиометра и панорамного измерителя, показанных на Рис. 7 и 8 предложена модель, которая на основе соотношении (4) связывает аномальное неравновесное излучение образца сплава Ti-Ni в диапазоне 8 мм, регистрируемое радиометром с измеренной при помощи панорамного измерителя зависимостью коэффициента отражения. Построен график (Рис. 9а) яркостной температуры образцы Тобр от времени по формуле:
Т = Тобр(1-R) + TподсветкиR, (5)
где R – коэффициент отражения, найденный по данным панорамного измерителя, Тподсветки – параметр подгонки, зависящий от показания аттенюатора. На Рис. 9а его значение принято равным 180 К. Сравнение эксперимента и расчета дает их удовлетворительное качественное согласие (сравните Рис. 9 а и б).
|
|
||||||
|
Рис. 7. Показано семейство временных зависимостей сигнала радиометра для сплава Ti-Ni при термоциклированиии вблизи мартенситного ФП (от 0 до 100 °С). Наблюдаются яркие аномалии сигнала при термоциклировании в районе мартенситного ФП первого рода. Параметр – эффективная температура излучения подсветки (0% аттенюатора отвечает минимальной температуре подсветки – температуре жидкого азота, 100% поглощения аттенюатора – комнатная температура подсветки). Относительная величина немонотонных аномалий зависимости резко снижается с увеличением поглощения аттенюатора.
|
||||||
|
|
||||||
|
Рис. 8. Температурная зависимость коэффициента отражения сплава Ti-Ni в диапазоне 8 мм, измеренная вблизи мартенситного ФП при помощи панорамного измерителя мощности.
|
||||||
Таким образом, полученные экспериментальные данные позволяют высказать гипотезу о наличии при мартенситном ФП специфического излучения. Его вклад находится на уровне нескольких процентов от основного вклада подчиняющегося законам Планка и Стефана - Больцмана. Вклад этого излучения в теплопроводность вакуумного промежутка должен быть учтен при проведении экспериментов по передаче тепла в вакуумном промежутке между двумя поверхностями слоистых структур с ФП.
4. Заключение
В заключении сформулируем основные результаты работы.
1. Разработана экспериментальная установка для изучения электромагнитного отклика на внешнее воздействие и самопроизвольного (квазитеплового) излучения образцов с ФП в диапазоне 8 мм (28-32 ГГц). Методика позволяет проводить in situ измерения, как электромагнитного излучения образца, так и измерения низкочастотной магнитной восприимчивости, отражающей протекание магнитного и структурного ФП в образце.
2. При экспериментальном изучении квазитеплового излучения образцов ферромагнитного сплава Гейслера Ni2,14Mn0,81GaFe0,05 в диапазоне 8 мм (28-32 ГГц) обнаружена аномальная немонотонная зависимость излучения от температуры вблизи мартенситного ФП (330 - 345 K). Разделены вклады в сигнал от собственного излучения образца и отраженного электромагнитного фона. Влияние кинетики ФП на характер ММ излучения образца изучалось при изменении скорости нагрева/охлаждения от 0,1 К/с до 10 К/с. Показано, что вклад собственного излучения возрастает при увеличении скорости изменения температуры. Это также подтверждает, что обнаруженные аномалии не подчиняются формуле Планка и закону Стефана-Больцмана и отвечают собственному излучению ЭМВ при неравновесных процессах, связанных с ФП. Количественно аномалии, связанные с ФП могут оцениваться порядка нескольких процентов теплового излучения образца.
3. Обнаружены аномальные флуктуации излучения вблизи точки Кюри (360 К) ферромагнитного сплава Гейслера Ni2,14Mn0,81GaFe0,05. Разделение вкладов флуктуаций собственного излучения и коэффициента отражения показало, что они проявляются только при снижении температуры внешней фоновой подсветки, и, следовательно, обусловлены аномалиями коэффициента пропускания вблизи точки Кюри.
4. В сплаве TiNi исследовано радиометрическим методом собственное излучение и коэффициент отражения ЭМВ в диапазоне 28- 32 ГГц. В интервале температур вблизи термоупругого структурного мартенситного ФП (290 – 315 К) обнаружены аномалии собственного излучения и коэффициента отражения, связанные с неравновесными процессами при ФП. Предложена модель, связывающая аномалии коэффициента отражения и интенсивности собственного излучения, проведено численное моделирование и получено качественное согласие расчетных и экспериментальных результатов.
Работа выполнена при поддержке РФФИ, грант № 12-07-00656.
Литература
1. G.E.W. Bauer, E.Saitoh, B.J.van Wees. Spin caloritronics // Nature Materials. 2012, V. 11. P. 391-399.
2. Dejene, F. K.; Flipse, J.; Bauer, G. E. W.; et al. Spin heat accumulation and spin-dependent temperatures in nanopillar spin valves // Nature Physics, 2013, V. 9, No 10. P. 635-638.
3. Dejene, F. K.; Flipse, J.; van Wees, B. J. Spin-dependent Seebeck coefficients of Ni80Fe20 and Co in nanopillar spin valves // Phys. Rev. B 2012, V. 86, No. 2, 024436.
4. W. Jiang, P. Upadhyaya, Y. Fan, Direct Imaging of Thermally Driven DomainWall Motion in Magnetic Insulators. Pys. Rev. Lett. 2013, V. 110, 177202.
5. Ni. Yun, Y. Kailun, H. Fu, et al. Spin Seebeck Effect and Thermal Colossal Magnetoresistance in Graphene Nanoribbon Heterojunction // Scientific Rep. 2013, V. 3, 1380.
6. N. Z. Ping. Thermally induced spin transport in two-dimensional ferromagnetic gapped grapheme. EPL (Europhysics Letters) 2013, V. 101. 57008.
7. Y. Ni, K.-L.Yao, H.-H. Fu, et al. The transport properties and new device design: the case of 6,6,12-graphyne nanoribbons // Nanoscale. 2013, V. 5, No 10. P. 4468-4475.
8. M. Zeng, W. Huang, G. Liang. Spin-dependent thermoelectric effects in graphene-based spin valves // Nanoscale. 2013, V. 5, No 1. P.200-208.
9. M. Zeng, Y. Feng, G. Liang. Graphene-based Spin Caloritronics // Nano Lett. 2011, V. 11, No 3. P. 1369-1373.
10. M. Martín-González, O. Caballero-Calero, P. Díaz-Chao. Nanoengineering thermoelectrics for 21st century: Energy harvesting and other trends in the field. Renewable and Sustainable // Energy Reviews. 2013, V. 24. P. 288–305.
11. А.И.Волокитин, Б.Петерсон. Радиационная передача тепла и бесконтактное трение между наноструктурами // УФН. 2007, т. 177, № 9. С. 921- 951.
12. I. Altfeder, A. Voevodin, K. Ajit Vacuum Phonon Tunneling // Phys. Rev. Lett. 2010, V.105, 166101.
13. A. Kitel, W. Muller-Hirsch, J. Parisi, et al. Near-Field Heat Transfer in a Scanning Thermal Microscope // Phys. Rev. Lett. 2005, V.95, 224301.
14. Балакирев М.К., Горчаков А.В. Просачивание упругой волны через зазор между пьезоэлектриками // ФТТ, 1977. Т. 19. № 2. с. 571-572.
15. Балакирев М.К., Богданов С.В., Горчаков А.В. Туннелирование ультразвуковой волны через щель между кристаллами иодата лития // ФТТ, 1978, Т. 20, № 2. C. 588-590.
16. Гуляев Ю.В., Плесский В.П. Резонансное прохождение акустической волны через щель между пьезоэлектриками // ФТТ. 1978, Т. 20, № 1. C. 133-138.
17. С.М. Рытов. Теория электрических флуктуаций и теплового излучения. Издательство АН СССР, Москва 1953. С. 232.
18. E. Rousseau, A. Siria, G. Jourdan, et al. Radiative heat transfer at the nanoscale // Nature Photonics. 2009, V. 3. P. 514 - 517.
19. Polder D., Van Hove M. Theory of Radiative Heat Transfer between Closely Spaced Bodies // Phys. Rev. B. 1971, V. 4. P. 3303-3314.
20. J.-P. Mulet, K. Joulain, R. Carminati, et al. Enhanced radiative heat transfer at nanometric distances // Microscale Thermophysical Engineering. 2002, V. 6, Issue 3. P. 209-222.
21. M. E. Perel'man, V. A. Tatartchenko. Phase transitions of the first kind as radiation processes. Physics Letters A 2008 V. 372. P. 2480–2483.
22. Г.С. Бордонский, А.А. Гурулев, А.О. Орлов, С.В. Цыренжапов. Усиление микроволнового излучения во льду при фазовом переходе, вызванном давлением // Письма в ЖТФ. 2012, Т. 38, С. 30 – 36.
23. С.А.Салль, А.П.Смирнов. Фазовопереходное излучение и рост новой фазы // ЖТФ. 2000, Т. 70, № 7. С. 35 – 39.
24. C. Grojean, G. Servant. Gravitational waves from phase transitions at the electroweak scale and beyond // Phis. Rev. D. 2007. V. 75, 043507.
25. Wang, KT, Brewster, MQ. Phase-transition radiation in vapor condensation process // Int. Comm. Heat Mass Transf. 2010, V.37. P. 945-949.
26. V.A. Tatartchenko. Infrared characteristic radiation of water condensation and freezing in connection with atmospheric phenomena; part 2: New data / Earth-Science Reviews. 2011, V. 107. P. 311– 319.
27. C. M. Jaworski, J. Yang, S. Mack, et al. Observation of the spin-Seebeck effect in a ferromagnetic semiconductor // Nature Materials. 2010. V. 9. P, 898–903.
28. С.Нестеров, А.Холопкин. Вакуумные туннельные диоды // Наноиндустрия. 2014, №6 (52). C. 46-50.
29. Y. Hisinuma, T.H.Gaballe, B.Y.Moyzhez. Refrigeration by combined tunneling and thermoionic emission in vacuum // Appl. Phys. Lett. 2001. V. 78. P. 2752-2754.
30. Belbachir, R.Y., An, Z., Ono, T. Thermal investigation of a micro-gap thermionic power generator // Journal of Micromechanics and Microengineering. 2014. V. 24, 085009.
31. Giazotto, F., Heikkilä, T.T., Luukanen, et al. Opportunities for mesoscopics in thermometry and refrigeration // Reviews of Modern Physics. 2006. V. 78 (1), P. 217-274.
32. А.Д.Божко, В.Д.Бучельников, А.Н.Васильев, И.Е.Дикштейн, С.М.Селецкий. В.В.Ховайло. Фазовые переходы в ферромагнит-ных сплавах Ni2+xMn1-xGa // Письма в ЖЭТФ. 1998. т. 67. № 3. с. 214-218.
33. А.Божко, А.Васильев, В.Ховайло, И.Дикштейн, В.Коледов,С.Сел-ецкий,А.Тулайко-ва,А.Черечукин, В.Бучельников. Магнитные и структурные фазо-вые переходы в ферромагнитных сплавах Mi2+xMn1-xGa с памятью формы // ЖЭТФ. 1999. т.115. № 5. с. 1740-1755.
34. Cherechukin, A.A., Dikshtein, I.E., Ermakov, D.I., et al. Shape memory effect due to magnetic field-induced thermoelastic martensitic transformation in polycrystalline Ni-Mn-Fe-Ga alloy // Physics Letters. 2001, V. A 291 (2-3), P. 175-183.
35. V.Buchelnikov, I.Dikshtein, R.Grechishkin, T.Khudaverdyan, V.Koledov, Yu.Kuzavko ,I.Nazarkin,T.Takagi. Ultrasound induced martensitic transition in ferromagnetic Ni2.15Mn0.81Fe0.04Ga shape memory alloy // JMMM. 2004. Vol. 272-276.p.2025-2026.