УДК 535.36
ЛАЗЕРНОЕ ФОРМИРОВАНИЕ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОННЫХ СГУСТКОВ СУБМИКРОННОЙ ДЛИТЕЛЬНОСТИ ИЗ ПЛАЗМЕННЫХ СЛОЕВ
В. В. Кулагин1,2, В. Н. Корниенко2, В. А. Черепенин2
1Государственный астрономический институт им. П. К. Штернберга
Московского государственного университета им. М. В. Ломоносова
2Институт радиотехники и электроники им. В.А. Котельникова РАН
Статья получена 20 октября 2014 г.
Аннотация. Предложено и с помощью численного моделирования исследовано формирование релятивистских электронных сгустков субмикронной длительности из плазменных слоев под воздействием сверхмощного лазерного импульса. Показано, что возможно формирование электронных сгустков с минимальной толщиной в несколько десятков нанометров при энергиях в десятки и сотни МэВ. При этом заряд сгустка может составлять от единиц пикокулон до нескольких нанокулон. Исследовано влияние толщины и продольного профиля плазменного слоя, а также амплитуды лазерного импульса на характеристики формируемых электронных сгустков и предложены простые аналитические выражения для оценки их параметров.
Ключевые слова: сверхмощные лазерные импульсы, плазменные слои, релятивистские субмикронные электронные сгустки.
Abstract: Forming relativistic submicron electron bunches from plasma layers under the action of a super-intense laser pulse was proposed and studied with computer simulation. It was shown that the electron bunches can have a minimal thickness of tens of nanometers and energies of tens to hundreds of MeV. The charge of the bunches can be from picocoulombs to nanocoulombs. The role of the thickness and profile of gas layer and laser amplitude on characteristics of the relativistic electron bunches was studied. Simple analytical expressions were proposed to estimate parameters of the electron bunches.
Key words: super-intense laser pulses, plasma layers, relativistic submicron electron bunches.
1. Введение
Лазерное ускорение электронов и формирование одиночных электронных сгустков активно развивается в настоящее время во многих лабораториях мира. Основным условием использования таких сгустков в приложениях является возможность контроля их параметров, таких, как длительность, заряд в сгустке, средняя энергия, разброс энергии и т.д.. В настоящее время предложено несколько способов генерации сверхкоротких электронных пучков с помощью лазерных импульсов. В первом случае лазерный импульс с релятивистской амплитудой падает на поверхность плотной сверхкритической плазмы. Сила Лоренца выталкивает электроны один или два раза за период из плазмы (схема на отражение) или ускоряет электроны преплазмы в направлении лазерного импульса с последующим прохождением через плазму (схема на прохождение) [1-4]. В этом механизме эжекция и ускорение электронов носят нерегулярный характер, что объясняет широкий разброс энергий электронов в пучке и невозможность контролировать его параметры. Длительность электронного сгустка оказывается порядка длительности лазерного импульса, к тому же в пучке имеется модуляция плотности (микробанчинг), а возможность выделения отдельного микросгустка до конца не ясна.
Во втором случае сверхкороткие электронные пучки могут быть получены в плазме низкой (докритической) плотности с помощью применения механизма ускорения электронов в кильватерной волне лазерного импульса [5-7]. Однако длина электронного сгустка в этой схеме составляет не менее нескольких микрон, или десятки фемтосекунд, что явно недостаточно для многих применений.
Идея синхронного ускорения электронов нанопленки
сверхмощным неадиабатическим лазерным импульсом была впервые предложена в [8] и
затем были исследованы характеристики формирующихся релятивистских электронных
сгустков [9]. При перпендикулярном падении неадиабатического лазерного импульса
релятивистской амплитуды (
где 
и 
- размерная и безразмерная амплитуды лазерного
импульса с частотой 
и длиной волны 
, 
и 
– абсолютная величина заряда и массы электрона, 
- скорость света в вакууме) на
нанопленку может происходить одновременное продольное (по отношению к оси луча
лазера) смещение всех электронов нанопленки под действием продольной компоненты
силы Лоренца. При достаточно большой амплитуде поля эта сила разгоняет
электроны нанопленки до релятивистских скоростей. В результате может
сформироваться релятивистское электронное зеркало - электронный сгусток с
диаметром порядка нескольких микрон при толщине в несколько нанометров и менее.
Необходимым условием формирования релятивистского электронного зеркала является
превышение амплитудой лазерного импульса определенного порога, зависящего от
толщины и материала нанопленки [9]. Указанная схема имеет следующие свойства: а).
формируется одиночный электронный сгусток; б). заряд сгустка может составлять
несколько десятков нанокулон; в). параметры сгустка могут легко
контролироваться изменением параметров лазерного импульса и нанопленки.
2. Формирование релятивистских электронных сгустков из газовых слоев
Аналогичный подход может быть применен и к формированию релятивистских электронных зеркал из газовых слоев докритической плотности. Физика взаимодействия здесь существенно отличается от случая твердотельных мишеней, поскольку лазерный импульс проходит через газовую мишень без существенного отражения. Тем не менее, и в случае падения лазерного импульса релятивистской интенсивности на плазменный слой докритической плотности продольная компонента силы Лоренца также вызывает продольное смещение электронов плазмы и может разгонять их до релятивистских скоростей. Если амплитуда импульса достаточно велика, а электронная плотность слоя умеренная, то возможен эффект полного вытеснения электронов из слоя плазмы. Импульс распространяется в плазме, ускоряя и захватывая все большее количество электронов. Если толщина плазменного слоя меньше некоторого порога, определяемого амплитудой и длительностью лазерного импульса, то также, как и в случае нанопленок, может быть сформировано релятивистское электронное зеркало, диаметр которого определяется диаметром лазерного импульса, а толщина уже составляет несколько десятков или сотен нанометров. В случае нанопленки твердотельная плотность мишени может накладывать определенные ограничения на параметры зеркал, в частности, на максимальную энергию и на разброс энергий электронов в зеркале, что определяется относительно большой безразмерной поверхностной плотностью заряда электронов нанопленки (для одного атомного слоя графена эта величина оказывается порядка единицы). Безразмерная поверхностная плотность заряда электронов плазменного слоя определеляется в соответствии со следующим выражением:
(1)
Здесь 
- размерная поверхностная плотность заряда, 
– концентрация электронов в плазме, 
– толщина плазменного слоя, а 
– плазменная частота. В этом смысле электронные сгустки, формируемые из
газовой струи, могут обладать значительно меньшей безразмерной поверхностной
плотностью электронов (0.01 и менее), что значительно расширяет их область
применимости, в том числе, для аттосекундных воздействий пробного пучка в
экспериментах типа «pump-probe» и для генерации когерентных импульсов
рентгеновского диапазона с помощью рассеяния встречного лазерного пучка.
3. Динамика формирования релятивистских электронных сгустков
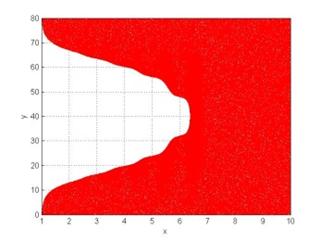
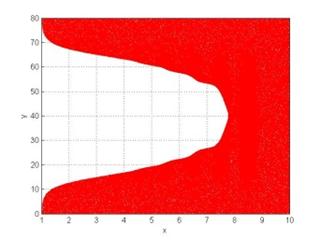
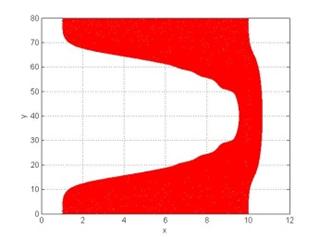
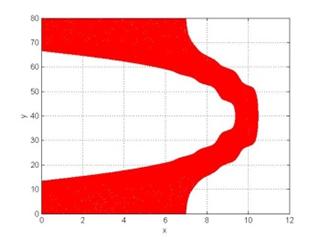
Ниже представлены результаты численного моделирования процесса формирования релятивистских электронных зеркал из плазменного слоя при падении мощного лазерного импульса с крутым фронтом (длительность фронта – доли периода импульса). Формирование электронного сгустка из плазменного слоя толщиной 9 микрометров представлено на рис. 1 для разных моментов времени. Отношение плазменной частоты слоя к частоте лазерного импульса составляет 0.02, безразмерная амплитуда лазерного импульса равна 3, диаметр 20 мкм, длина волны 1 мкм, импульс имеет вид отрезка синусоиды длиной 5 длин волн, что соответствует неадиабатической форме импульса, когда уже первый полуцикл имеет амплитуду, близкую к максимальной амплитуде импульса. Из рисунка видно, как лазерный импульс последовательно вытесняет все электроны из плазменного слоя, формируя короткий сгусток увеличенной плотности. Для количественных оценок воспользуемся моделью движения одиночного электрона в поле плоской волны. Эти уравнения имеют аналитические решения [10] для произвольной временной зависимости амплитуды поля. В нашем случае для безразмерной амплитуды импульса, равной 3, период скольжения электрона (переход с одного цикла поля на следующий для одиночного электрона в поле импульса) составляет порядка 7 длин волн, поэтому такой импульс при падении на слой толщиной 9 длин волн не может сформировать зеркала толщиной менее длины волны. Действительно, на рис. 2 представлен увеличенный вид формирующегося электронного сгустка, соответствующий рис. 1(в), где видно наличие двух слоев электронного зеркала с увеличенной плотностью, разделенных разреженным слоем. Для импульса с амплитудой, равной 5, период скольжения составляет уже порядка 19 длин волн (квадратичная зависимость от амплитуды поля), и такой импульс уже может сформировать релятивистское электронное зеркало с толщиной, значительно меньшей длины волны (рис. 3). Здесь толщина сгустка на оси составляет порядка 190 нм.
|
(а) |
(б) |
|
(в) |
(г) |
Рис. 1. Формирование релятивистского электронного зеркала из плазменного слоя неадиабатическим лазерным импульсом (пространственное распределение электронов): (а) – 6 периодов, (б) – 8 периодов, (в) – 10 периодов и (г) – 13 периодов от начала взаимодействия. Толщина слоя составляет 9 длин волн, отношение плазменной частоты слоя к частоте лазерного импульса равно 0.02, безразмерная амплитуда лазерного импульса равна 3, длина волны 1 мкм, диаметр 20 мкм, импульс имеет вид отрезка синусоиды длиной 5 длин волн. Координаты нормированы на длину волны.
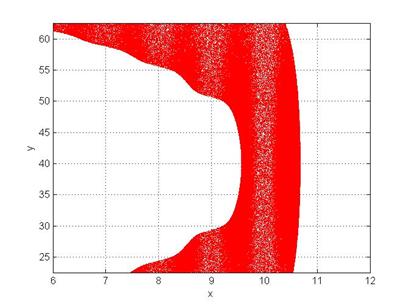
Рис. 2. Увеличенный вид формирующегося электронного сгустка, соответствующий рис. 1(в).
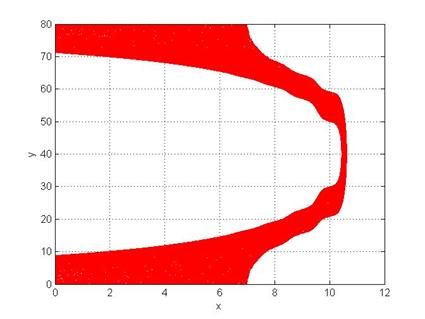
Рис. 3. Релятивистское электронное зеркало, формируемое из плазменного слоя неадиабатическим лазерным импульсом с безразмерной амплитудой, равной 5, в момент времени, равный 13 периодам от начала взаимодействия. Остальные параметры такие же, как на рис. 1.
4. Толщина релятивистских электронных сгустков
Зависимость толщины сгустка электронов на оси от амплитуды лазерного импульса представлена на рис. 4. Плавной зеленой кривой показан аналитический вид зависимости, полученный из уравнений движения одиночного электрона в поле лазерного импульса [10]; синей кривой, маркированной кружками – результаты для минимально достижимой толщины электронного зеркала по результатам двумерного численного моделирования; красной кривой, маркированной квадратами – толщина зеркала при максимальной энергии составляющих его электронов (также по данным численного моделирования). Увеличение амплитуды лазерного импульса приводит к увеличению продольного импульса и энергии электронного сгустка (квадратичная зависимость), что в свою очередь вызывает уменьшение толщины зеркала обратно пропорционально энергии электронов. Аналитические зависимости, полученные из уравнений движения одиночного электрона в поле электромагнитной волны [10], показывают, что минимальная толщина электронного сгустка должна реализовываться при максимальной энергии электронов в нем. Однако в общем случае минимальная толщина релятивистского электронного зеркала и максимальная энергия составляющих его электронов достигаются в разное время, что связано с действием кулоновских сил. Таким образом, результаты моделирований показывают, что при безразмерной амплитуде импульса, равной 10-20, возможно формирование релятивистских электронных зеркал хорошего качества с толщиной в несколько десятков нанометров. Из рис. 4 следует также, что простые аналитические оценки для движения одиночного электрона в поле лазерного импульса позволяют предсказать характеристики релятивистских электронных зеркал с достаточной точностью при использовании слоев плазмы с умеренной плотностью.
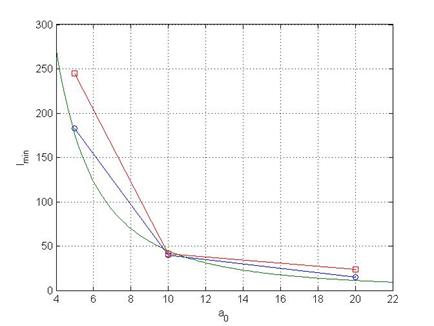
Рис. 4. Зависимость минимальной толщины сгустка электронов на оси (в нм) от амплитуды лазерного импульса (параметры лазера и плазменного слоя соответствуют рис. 1). Плавной зеленой кривой показан аналитический вид зависимости, полученный из уравнений движения одиночного электрона в поле лазерного импульса [10]; синей кривой, маркированной кружками – результаты для минимально достижимой толщины из двумерного численного моделирования; красной кривой, маркированной квадратами – толщина зеркала при максимальной энергии составляющих его электронов (также результаты численного моделирования).
5. Формирования сгустков из слоев плазмы с переменной плотностью
Было численно исследовано также формирование релятивистских электронных зеркал из плазменных слоев с изменяющимся профилем плотности. В целом характер процесса остается таким же, как и для слоев с постоянной плотностью при условии, что безразмерные поверхностные плотности электронов получающихся сгустков одинаковы.
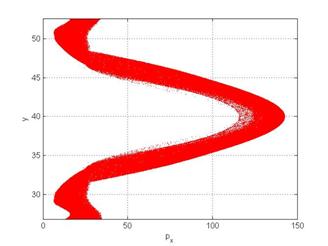
Релятивистское электронное зеркало, сформированное из слоя плазмы толщиной 40 мкм (линейное увеличение плотности на длине 10 мкм и затем постоянная плотность на длине 30 мкм) лазерным импульсом с амплитудой, равной 10, представлено на рис. 5 (60 периодов от начала взаимодействия). Отношение плазменной частоты слоя в области плоского участка к частоте лазерного импульса составляет 0.02, диаметр импульса 20 мкм. Распределение электронов в пространстве показано на рис. 5(а), а фазовое пространство для электронов (нормированный продольный импульс – поперечная координата) - на рис. 5(б). Толщина релятивистского электронного зеркала составляет 175 нм, максимальный нормированный продольный импульс равен 143 (энергия порядка 70 МэВ), разброс энергии электронов в зеркале равен 18%. Диаметр зеркала приблизительно равен диаметру лазерного импульса и составляет около 20 мкм. Заряд сгустка может составлять от единиц пикокулон до нескольких нанокулон в зависимости от начальной плотности электронов плазменного слоя, его толщины и диаметра лазерного импульса. Для формирования такого зеркала требуется лазер с мощностью порядка 200 ТВт.
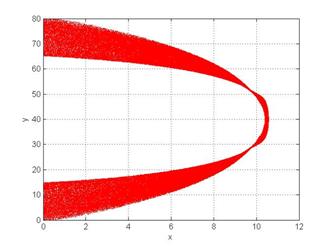
(а) (б)
Рис. 5. Релятивистское электронное зеркало, сформированное из плазменного слоя толщиной 40 мкм неадиабатическим лазерным импульсом с безразмерной амплитудой, равной 10, в момент времени, равный 60 периодам от начала взаимодействия. Отношение плазменной частоты слоя к частоте лазерного импульса равно 0.02, диаметр импульса 20 мкм. (а) – распределение электронов в пространстве, (б) - фазовое пространство для электронов (нормированный продольный импульс – поперечная координата).
Таким образом, неадиабатические лазерные импульсы могут быть с успехом использованы для формирования релятивистских электронных зеркал с заданными параметрами из плазменных слоев толщиной до 200-300 мкм.
6. Заключение
В работе показано, что для относительно умеренных безразмерных амплитуд импульса порядка 3-20 возможно формирование электронных сгустков с минимальной толщиной в несколько десятков нанометров (длительность – десятки аттосекунд) при энергиях в десятки и даже сотни МэВ для достаточно мощного лазерного импульса (субпетаваттной мощности). При этом заряд сгустка может составлять от единиц пикокулон до нескольких нанокулон. Исследовано влияние начальной толщины и продольного профиля плазменного слоя, а также амплитуды лазерного импульса на характеристики формируемых электронных сгустков и предложены простые аналитические оценки для возможных параметров зеркал.
Исследование выполнено за счет гранта Российского научного фонда
(проект №14-12-01259).
Литература
1. R. Kodama, K. A. Tanaka, Y. Sentokuet al. // Long-Scale Jet Formation with Specularly Reflected Light in Ultraintense Laser-Plasma Interactions. Phys. Rev. Lett. 84, 674 (2000).
2. N. Naumova, I. Sokolov, J. Nees, A. Maksimchuk, V. Yanovsky, and G. Mourou // Attosecond Electron Bunches. Phys. Rev. Lett. 2004. V. 93. P. 195003.
3. S. D. Baton, J. J. Santos, F. Amiranoff et al. // Evidence of Ultrashort Electron Bunches in Laser-Plasma Interactions at Relativistic Intensities. Phys. Rev. Lett. 2003. V. 91. P. 105001.
4. Jian Zheng, K. A. Tanaka, T. Sato et al. // Study of Hot Electrons by Measurement of Optical Emission from the Rear Surface of a Metallic Foil Irradiated with Ultraintense Laser Pulse. Phys. Rev. Lett. 2004. V. 92. P. 165001.
5. D. Umstadter, J.K. Kim, and E. Dodd // Laser Injection of Ultrashort Electron Pulses into Wakefield Plasma Waves. Phys. Rev. Lett. 1996. V. 76. P. 2073.
6. A. G. Khachatryan, F. A. van Goor, and K.-J. Boller et al. // Extremely short relativistic-electron-bunch generation in the laser wakefield via novel bunch injection scheme. Phys. Rev. ST Accel. Beams. 2004. V. 7. P. 121301.
7. N. Hafz, V. Kulagin, J. Lee, H. Suk. // Near-GeV electron beam from a laser wakefield accelerator in the bubble regime. Nucl. Instrum. Methods Phys. Res., Sect. A. 2005. V. 554. P. 49.
8. Victor V. Kulagin, Vladimir A. Cherepenin, Yuri V. Gulyaev, Vladimir N. Kornienko, Ki Hong Pae, Victor V. Valuev, Jongmin Lee, and Hyyong Suk. Characteristics of relativistic electron mirrors generated by an ultrashort nonadiabatic laser pulse from a nanofilm, Physical Review E, 80, 016404 (2009).
9. Kulagin V.V., Cherepenin V.A., Hur M.S., Suk H. Theoretical Investigation of Controlled Generation of a Dense Attosecond Relativistic Electron Bunch from the Interaction of an Ultrashort Laser Pulse with a Nanofilm. Phys. Rev. Lett., 99, 124801 (2007).
10. Л. Д. Ландау, Е. М. Лифшиц, Теория поля, М.: Наука, 1988. Глава 6, параграф 48.