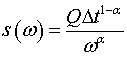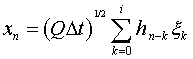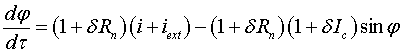МОДЕЛИРОВАНИЕ фликкер-шума В Бикристаллических джозефсоновскИХ переходаХ
В. Н. Губанков 1, В. В. Павловский 1, А. В. Снежко 1,2
1 Институт радиотехники и электроники им. В.А. Котельникова РАН
2 Московский физико-технический институт
Статья поступила в редакцию 30 ноября 2015 г.
Аннотация. В работе представлена методика вычислений вольтамперной характеристики джозефсоновского перехода и отклика тока через переход на внешнее электромагнитное излучение в присутствие 1/f флуктуаций критического тока и сопротивления в нормальном состоянии (фликкер-шума), а также результаты исследования влияния фликкер-шума на детекторные характеристики бикристаллического ДП из YBa2Cu3O7-x с наклонными осями [001]. Показано, что высокочастотные характеристики джозефсоновского перехода в случае фликкер-шума качественно совпадают с аналогичными характеристиками, полученными для случая тепловых шумов. При этом в первом случае возможно увеличение частотной полосы широкополосного детектирования ДП на ~18%. Из вычислений селективного детекторного отклика следует, что ширина линии генерации ДП в случае фликкер-шума в ~2 раза превосходит соответствующий параметр для случая тепловых шумов при одинаковых амплитудах отклика. Таким образом полученные результаты продемонстрировали возможность существенного влияния фликкер-шумов на высокочастотные характеристики бикристаллических ДП.
Ключевые слова: терагерцовая электроника, сверхпроводимость, джозефсоновский переход, фликкер-шум.
Abstract. Calculations of Josephson junction (JJ) IV-curve and response on external electromagnetic radiation in the presence of critical current and normal state resistance 1/f fluctuations (flicker noise) were performed. The influence of flicker-noise on JJ wide-band and selective detecting characteristics was investigated and compared with the influence of thermal noise. It was shown a qualitative coincidence of high-frequency JJ characteristics in the cases of flicker noise and normal current thermal fluctuations. In the case of flicker noise about 18% enhancement of classical detection frequency band is possible. A JJ oscillation linewidth is about twice greater in the case of flicker noise than in the case of thermal noise at the equal response amplitudes. The results obtained show a possible significant influence of 1/f fluctuations on high-frequency JJ characteristics.
Key words: terahertz electronics, superconductivity, Josephson junction, flicker noise.
Введение
Хорошо известно, что форма линии генерации джозефсоновского перехода (ДП) существенно зависит от флуктуационных процессов в ДП [1]. В связи с тем, что форма линии генерации определяет большинство основных характеристик ДП (вольтамперную характеристику, отклик на внешнее электромагнитное излучение и т.д.), большой интерес представляет исследование динамики ДП с учётом различных источников флуктуаций. К настоящему время хорошо изучено влияние тепловых флуктуаций тока нормальных квазичастиц на характеристики ДП. В то же время уже достаточно давно было экспериментально продемонстрировано присутствие флуктуаций критического тока Ic со спектральной плотностью 1/f (фликкер-шума) в туннельных ДП [2,3]. Тем не менее, влияние флуктуаций Iс на динамику ДП подробно не исследовалось. Особую актуальность эта проблема приобрела в связи с использованием ДП из высокотемпературных сверхпроводников. Как было продемонстрировано в целом ряде работ [4-6], в ДП из YBa2Cu3O7-x наблюдаются значительные флуктуации Ic и сопротивления ДП в нормальном состоянии Rn, причём характер флуктуаций меняется в зависимости от типа перехода. Так для бикристаллических ДП с вертикальными осями [001] характерна высокая степень неоднородности барьера между сверхпроводящими электродами. При этом туннелирование нормальных квазичастиц и куперовских пар происходит по различным каналам и флуктуации Ic и Rn не коррелированы. В случае ДП с наклонными осями [001] характеристическое напряжение ДП Vc=IcRn не зависит от Ic и Rn по отдельности, что приводит к антикорреляции флуктуаций DIc/Ic=‑DRn/Rn [6,7]. В настоящей работе представлена методика математического моделирования динамики ДП с учётом флуктуаций Ic и Rn, имеющих спектральную плотность вида 1/f, а также результаты вычисления зависимости дифференциального сопротивления ДП от напряжения Rd(V) и отклика тока ДП на внешнее монохроматическое электромагнитное излучение для случая антикоррелерованных флуктуаций Ic и Rn, характерных для бикристаллических переходов с наклонными осями [001] [6].
1. Основные уравнения и алгоритм решения
Для численного
моделирования случайного процесса со спектральной плотностью,
пропорциональной 1/f, где f
–
частота, используем алгоритм, предложенный в [8] и основанный на фильтрации
белого шума. Введём оператор ![]() , который преобразует
случайный процесс, соответствующий белому шуму w(t)
в случайный процесс с заданными спектральными свойствами x(t):
, который преобразует
случайный процесс, соответствующий белому шуму w(t)
в случайный процесс с заданными спектральными свойствами x(t):
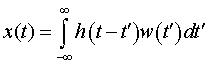 , (1)
, (1)
где
![]() . (2)
. (2)
Q – постоянная, характеризующая интенсивность шума.
Тогда спектральная плотность случайного процесса x(t) имеет вид:
![]() (3)
(3)
В дискретные моменты времени tn, такие, что tn+1-tn=Dt (2) и (3) имеют следующий вид:
![]() (4)
(4)
![]() (5)
(5)
где dij – символ Кронекера.
В дискретном случае удобно использовать z-преобразование (см., например, [9]):
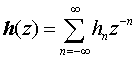 , (6)
, (6)
где hn=h(tn).
При этом
![]() . (7)
. (7)
Выберем h(z) в следующем виде [8]:
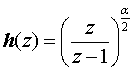 . (8)
. (8)
Тогда из (7) следует, что
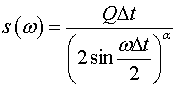 , (9)
, (9)
и при w<<2/Dt
В результате дискретную случайную последовательность xn со спектральной плотностью (9) можно получить следующим образом:
где
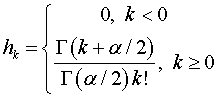 ,
,
G(x) – гамма-функция Эйлера, xn – последовательность случайных чисел со стандартным нормальным распределением, n,k=0,…,N-1
Для случая шума 1/f a=1 и (10) имеет вид:
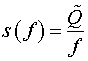 , (12)
, (12)
где 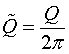 .
.
При этом минимальная частота fmin=(pNDt)-1. На рис. 1 изображена зависимость спектральной плотности случайного процесса (11) от частоты при Q=1, и N=105, Dt=4·10-3 сек. Было произведено усреднение спектральной плотности по 128 реализациям.
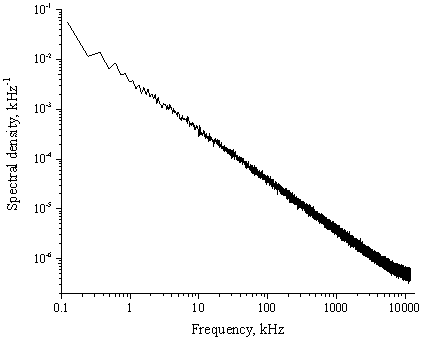
Рис. 1 Зависимость спектральной плотности случайного процесса (11) от частоты при a=1.
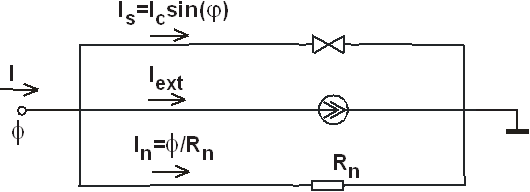
Рис. 2. Эквивалентная схема ДП в резистивной модели.
Динамика ДП исследовалась в рамках резистивной модели [1], которая достаточно хорошо описывает бикристаллические переходы из YBa2Cu3O7-x. Эквивалентная схема ДП изображена на рис. 2.
Уравнение для зависимости джозефсоновской разности фаз от времени j(t) имеет следующий вид:
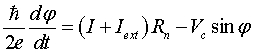 , (13)
, (13)
где I – полный ток через ДП, Iext – ток, создаваемый внешним электромагнитным излучением.
В случае
монохроматического излучения с частотой fext
![]() .
.
При учёте флуктуаций параметры Rn и Vc в общем случае зависят от времени:
![]() (14)
(14)
![]() ,
,
где ![]() .
. ![]() , DRn
– флуктуационные составляющие Ic
и
Rn.
, DRn
– флуктуационные составляющие Ic
и
Rn.
С учётом (14) уравнение (13) можно представить следующим образом:
где
![]() , i=I/Ic,
iext = Iext/Ic.
, i=I/Ic,
iext = Iext/Ic.
При
этом dIc(t)
и dRn(t)
представляют собой случайные процессы, спектральные плотности которых
соответствуют спектральным плотностям флуктуаций Ic
и
Rn.
В случае антикоррелированных флуктуаций ![]() . Решения (15) при
различных значениях I
использовались
для получения ВАХ и зависимости отклика тока ДП на внешнее излучение аналогично
тому, как это делалось в [10], а зависимость dRn(t)определялась
в соответствии с (11).
. Решения (15) при
различных значениях I
использовались
для получения ВАХ и зависимости отклика тока ДП на внешнее излучение аналогично
тому, как это делалось в [10], а зависимость dRn(t)определялась
в соответствии с (11).
2. Результаты вычислений и их обсуждение
Многие, в том числе высокочастотные, параметры ДП определяются его вольт-амперной характеристикой и её производными. На основе решения уравнения (15) были проведены вычисления различных характеристик ДП с Ic=1 мА и Rn=1 Ом. На рис. 3-5 они представлены сплошными линиями. Для сравнения были получены аналогичные характеристики для ДП с учётом флуктуаций тока нормальных квазичастиц, причём температура ДП подбиралась таким образом, чтобы величины максимумов характеристик в обоих случаях совпадали. Эти зависимости представлены на рисунках пунктирными линиями.
На рис. 3 представлены зависимости дифференциального сопротивления ДП от напряжения.
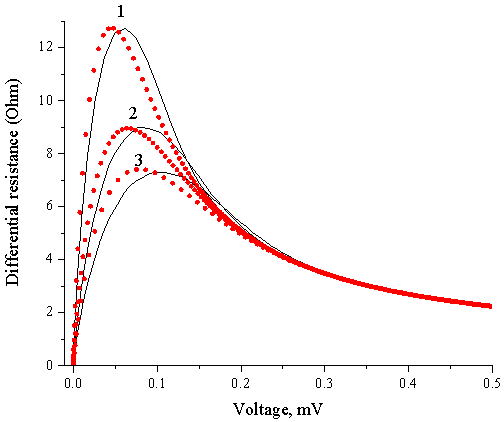
Рис. 3 Зависимости дифференциального сопротивления ДП от напряжения. Ic=1мА, Rn=1 Ом.
Значения Q равны 1×10-7 (1), 4×10-7 (2), 9×10-7 (3), значения температуры равны 4.5 К (1), 16.5 К (2), 24 К (3). Влияние флуктуаций приводит к появлению максимума зависимости Rd(V) в области низких напряжений. Положение максимума в случае Фликкер-шума сдвинуто относительно максимума в случае теплового шума в сторону высоких напряжений, что, в частности, приводит к увеличению низкочастотной границы при частотном анализе внешних электродинамических систем [11].
Характеристики ДП как широкополосного детектора определяются флуктуациями, и детекторный отклик пропорционален второй производной ВАХ d2V/dI2. На рис. 4 приведены зависимости второй производной ВАХ от напряжения, значения Q равны 1×10-7 (1), 4×10-7 (2), значения температуры равны 16.5 К (1) и 25 К (2).
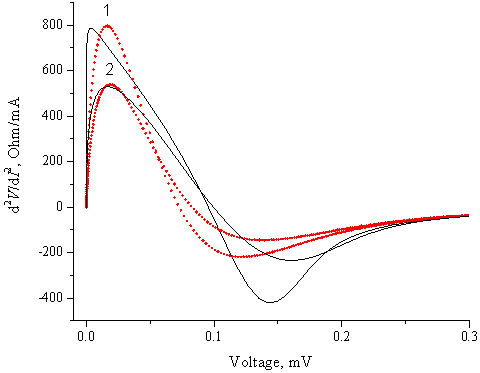
Рис. 4 Зависимости второй производной ВАХ ДП от напряжения.
При малой интенсивности флуктуаций (Q=1×10-7 и T=16.5 К) максимум детекторного отклика, определяемого фликкер-шумом, сдвинут в сторону низких частот по сравнению со случаем теплового шума. При более высокой интенсивности положения максимумов совпадают. В обоих случаях ширина максимума детекторного отклика при фликкер-шуме превышает аналогичную величину при тепловом шуме на ~18%, что соответствует более широкой частотной полосе детектирования в случае фликкер-шума.
На рис. 5 приведены зависимости отклика ДП на внешнее монохроматическое излучение от напряжения (селективного детекторного отклика):
![]() (16)
(16)
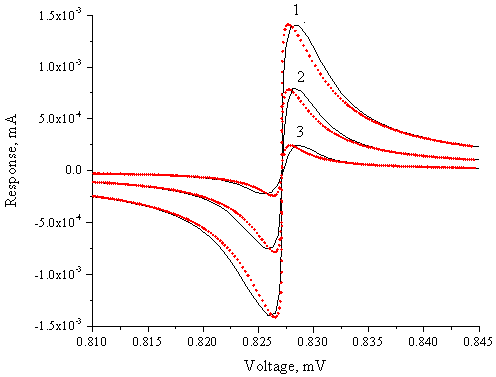
Рис.
5 Зависимость отклика ДП на внешнее излучение с частотой 200 ГГц и различными
амплитудами внешнего сигнала ![]() 1×10-3
(1), 4×10-3
(2), 6×10-3
(3). T=6К (1), 5.2 К
(2), 4.8 К (3). Q=1×10-7
1×10-3
(1), 4×10-3
(2), 6×10-3
(3). T=6К (1), 5.2 К
(2), 4.8 К (3). Q=1×10-7
В связи с тем, что ширина линии внешнего излучения равна 0, форма зависимости DI(V) при слабом сигнале определяется шириной линии собственной генерации ДП. Как следует из рис. 5, ширина особенности, связанной со ступенькой Шапиро ДП, для кривой (3) в случае фликкер-шума в ~2 раза превосходит аналогичный параметр, определяемый тепловыми флуктуациями. Фактически фликкер-шумы определяют предел, до которого можно понижать ширину линии генерации ДП при понижении температуры.
Заключение
В данной работе представлена методика вычислений вольт-амперной характеристики ДП и зависимости отклика тока через ДП на внешнее электромагнитное излучение от напряжения в присутствие 1/f флуктуаций Ic и Rn (фликкер-шума). С использованием разработанной методики были исследованы зависимости дифференциального сопротивления ДП, второй производной ВАХ ДП по току и отклика тока на внешнее монохроматическое излучение от напряжения для случая антикоррелированных флуктуаций Ic и Rn, характерных для бикристаллических ДП из YBa2Cu3O7-x с наклонными осями [001]. Результаты сравнивались с аналогичными характеристиками ДП, полученными при учёте тепловых флуктуаций тока нормальных квазичастиц. Из представленных результатов следует, что широкополосный и селективный детекторные отклики ДП в случае фликкер-шума качественно совпадают с аналогичными характеристиками, полученными для случая тепловых шумов. При этом в случае фликкер-шумов область напряжений широкополосного детектирования шире на ~18%, что может приводить к увеличению частотной полосы широкополосного детектирования. Было показано также, что ширина линии генерации ДП, в случае фликкер-шумов в ~2 раза превосходит соответствующий параметр для случая тепловых шумов при одинаковых амплитудах отклика. Это обстоятельство может приводить к стабилизации ширины линии генерации реальных ДП на некотором минимальном значении при уменьшении температуры. Таким образом полученные результаты продемонстрировали возможность существенного влияния фликкер-шумов на высокочастотные характеристики бикристаллических ДП.
Работа выполнена при финансовой поддержке Российского научного фонда (Грант № 14-19-01164).
Литература
1. Лихарев К.К, Ульрих Б.Т. Системы с джозефсоновскими контактами”, М., Изд-во МГУ,1978.
2. Wakai R.T. Van Harlingen D. J. Low-frequency noise and discrete charge trapping in small-area tunnel junction dc SQUID's. Appl. Phys. Lett., V.49, P. 593, 1986.
3. Savo B., Wellstood F.C., Clarke J. Low frequency excess noise in NbAl2O3Nb Josephson tunnel junctions. Appl. Phys. Lett., V.50, P. 1757, 1987.
4. Kawasaki M., Chaudhari P., Gupta A. 1/f Noise in YBa2Cu3O7–d Superconducting Bicrystal Grain-Boundary Junctions. // Phys. Rev. Lett. V. 68, N. 7, P, 1065, 1992
5. Hao L, Macfarlane J C, Pegrum C. M. Excess noise in YBa2Cu3O7–x film grain boundary Josephson junctions and devices. // Supercond. Sci. Technol., V. 9 P. 678, 1996.
6. Liatti M. V., Poppe U., Divin Y.Y.. Low-frequency voltage noise and electrical transport in [100]-tilt YBa2Cu3O7–x grain-boundary junctions. // Appl. Phys. Lett. V.88, P. 152504, 2006.
7. Лятти М.В. Детекторные характеристики YBa2Cu3O7–x бикристаллических джозефсоновских переходов с взаимнонаклоненными осями [001] в терагерцовой области частот. Диссертация на соискание ученой степени кандидата физико-математических наук. М. 2006.
8. Kasdin N. J. Discrete Simulation of Colored Noise and Stochastic Processes and 1/fa Power Law Noise Generation. // Proc. of the IEEE, V. 83, N. 5, P. 802 1995.
9. A.V. Oppenheim, R W Shafer. Digital Signal Processing. Prentice Hall, 1975,
10. Павловский В. В. Моделирование электромагнитной резонансной системы с джозефсоновским переходом. // Журнал радиоэлектроники, №3. 2013. URL: http://jre.cplire.ru/jre/mar13/4/text.pdf
11. Павловский В.В., Гундарева И.И., Волков О.Ю., Дивин Ю.Я., Губанков В.Н. Расширение частотного диапазона джозефсоновской импедансной спектроскопии. // Радиотехника и электроника, Т. 58, С. 977, 2013